[파이썬/Python] 백준 2342번: Dance Dance Revolution

📌 문제 : 백준 2342번

---

📌 문제 탐색하기

orders : 하나의 수열로 이루어진 지시 사항 ($len(orders) ≤ 100000$)

문제 풀이

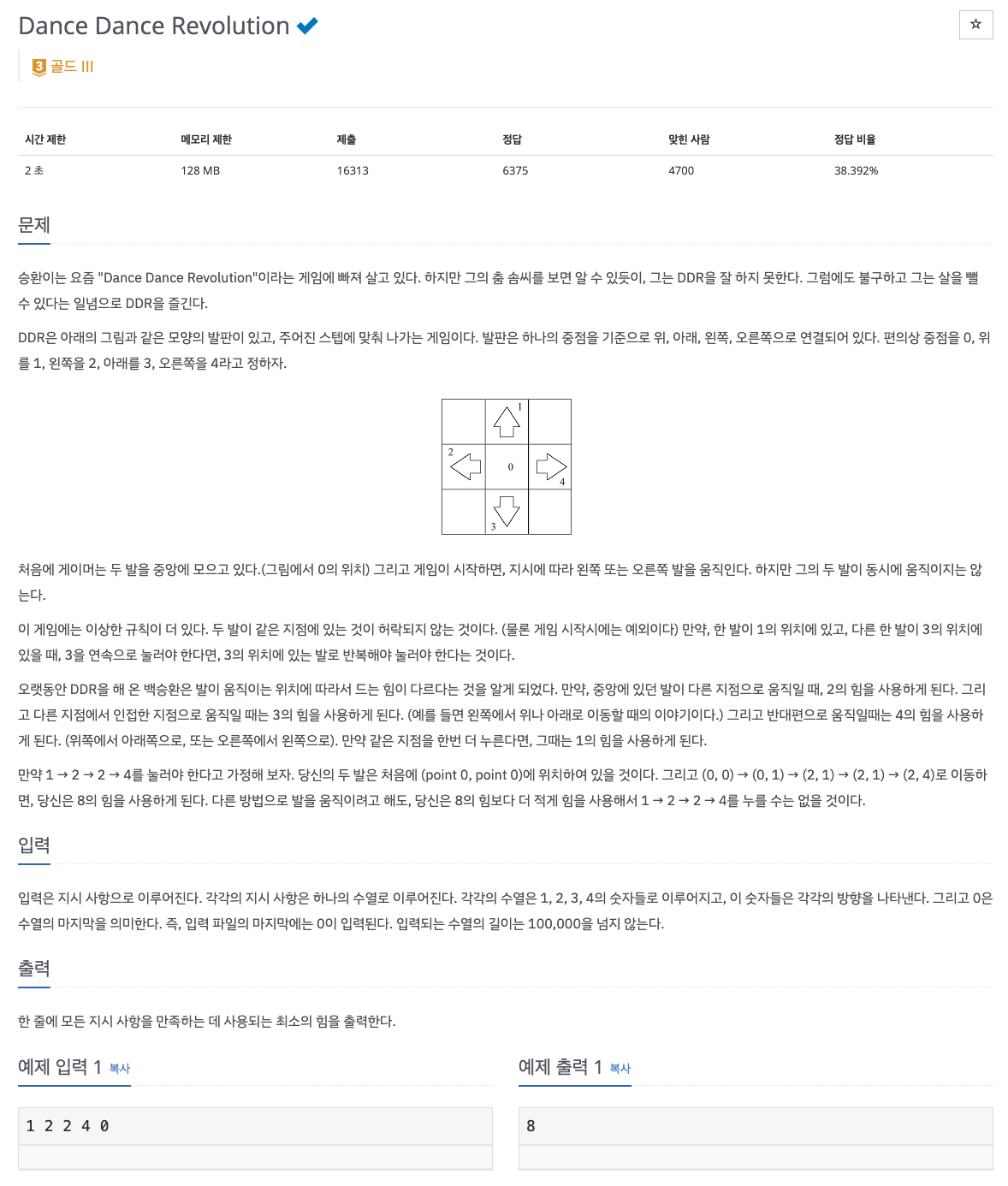
DDR의 발판은 하나의 중점을 기준으로 위, 아래, 왼쪽, 오른쪽이 있다.

0 -> 중점
1 -> 위
2 -> 왼쪽
3 -> 아래
4 -> 오른쪽

입력된 지시 사항에서의 0은 수열의 마지막을 의미한다.

⭐️ DDR 게임 규칙

• 중앙 0에서 시작
  • 왼발 또는 오른발 움직임
  • 동시 움직임 ❌
• 두 발이 같은 지점 위치 ❌
• 발 움직이는 위치에 따라 드는 힘 다름
  • 중앙 → 다른 지점 : 2의 힘 사용
  • 다른 지점 → 인접 지점 : 3의 힘
  • 반대편 이동 : 4의 힘
  • 같은 지점 : 1의 힘

위의 규칙을 지키면서 지시 사항을 모두 만족하는데 사용되는 최소의 힘을 구해야 한다.

매번 움직일 때마다 최소의 힘이 드는 방식으로 이동한다면 모든 지시 사항을 이행한 후 드는 힘의 총합은 최소가 될 수 있을 것이다.

따라서 다이나믹 프로그래밍 알고리즘으로 풀기 위한 점화식을 세울 수 있다.

먼저, 이동할 때마다 위치에 따른 드는 힘을 계산해주어야 하기 때문에 이동하는 4가지 경우를 판단하여 드는 힘을 반환하는 함수를 만들어준다.

1. 중앙에서 이동
2. 인접 지점 이동
3. 반대편 이동
4. 같은 지점 이동

그 후, 각 단계에서 저장해야할 상태는 현재 수행하는 지시 사항, 왼발의 위치, 오른발의 위치 3가지이므로 3차원의 DP 테이블을 만든다.
→ dp[orders][왼발 위치][오른발 위치] 형태로 정의

1. 왼발과 오른발 위치는 모두 5가지의 경우가 있고, 지시 사항은 최대 100000까지 가능하므로 이를 유의해서 크기를 결정한다.

2. 최솟값을 찾아가면서 테이블을 채워줘야 하기 때문에 테이블의 값은 최댓값으로 초기화해준다.

3. 시작 시 최소 힘이 0이므로 dp[0][0][0]은 0으로 채워준다.

점화식 계산 과정

1. 현재 위치에서 왼발, 오른발 각각에 대해 이동한 후의 드는 힘을 계산

2. 현재 드는 힘과 이동해서 계산된 드는 힘 둘 중 더 적은 힘이 드는 경우를 dp 테이블에 저장

   ### 수정 전
   # 왼발 이동
   dp[orders][left][right] = min(dp[orders][left][right], dp[orders-1][past_left][right] + force)
   # 오른발 이동
   dp[orders][left][right] = min(dp[orders][left][right], dp[orders-1][left][past_right] + force)
   
   ### 수정 후
   # 왼발 이동
   dp[i + 1][orders[i]][right] = min(dp[i + 1][orders[i]][right], dp[i][left][right] + force(left, orders[i]))
   # 오른발 이동
   dp[i + 1][left][orders[i]] = min(dp[i + 1][left][orders[i]], dp[i][left][right] + force(right, orders[i]))

• 수정 전과 같은 점화식으로 했다가 1회차 수정 사항 내용과 같은 원인으로 틀려서 점화식을 변경했다.

3. 위와 같이 마지막 0을 제외한 지시 사항들에 대해 이중 for문으로 점화식을 계산하며 dp 테이블 채우기

마지막으로 최소 드는 힘을 구하기 위해 전체 dp 테이블을 돌면서 최솟값을 갱신하고 그 결과를 출력한다.

가능한 시간복잡도

dp 테이블 채우기 → $O(len(orders) * 5 * 5)$

최종 시간복잡도
수열의 최대 길이가 100000이므로 제한 시간 2초 내에 연산이 가능하다.

알고리즘 선택

점화식을 이용한 dp 테이블 계산

---

📌 코드 설계하기

1. 드는 힘 반환하는 함수 정의
2. 지시 사항 입력
3. dp 테이블 정의
4. dp 테이블 채우기
5. 테이블에서 최소 드는 힘 구하기

---

📌 시도 회차 수정 사항

1회차

• dp 테이블을 채울 때 현재 위치보다 1 전의 값으로 비교하며 갱신하도록 했다. dp[0][0][0]=0으로 초기화했는데 dp[i-1] 값을 참조하도록 하니까 i=0인 경우 dp[-1] 값을 이용하면서 계산이 꼬였던 것 같다.

2회차

• 계속 출력이 더 작게 나오는 문제가 발생했다.
• 드는 힘을 계산하는 함수를 수정할 때 같은 지점으로 이동하는 경우에 드는 힘을 1이라고 해야 하는데 0이라고 하는 실수 때문에 발생한 문제였다.

---

📌 정답 코드

import sys

input = sys.stdin.readline

# 드는 힘 반환하는 함수 정의
def force(start, end):
    # 중앙에서 이동
    if start == 0:
        return 2

    # 같은 지점 이동
    elif start == end:
        return 1

    # 반대편 이동
    elif abs(start - end) == 2:
        return 4

    # 인접 지점 이동
    else:
        return 3


# 지시 사항 입력
orders = list(map(int, input().split()))

# dp 테이블 정의
dp = [[[500000 for _ in range(5)] for _ in range(5)] for _ in range(100001)]

# 시작 위치 초기화
dp[0][0][0] = 0

# dp 테이블 채우기
for i in range(len(orders) - 1):
    for left in range(5):
        for right in range(5):
            # 점화식 계산
            # 왼발 이동
            dp[i + 1][orders[i]][right] = min(dp[i + 1][orders[i]][right], dp[i][left][right] + force(left, orders[i]))
            # 오른발 이동
            dp[i + 1][left][orders[i]] = min(dp[i + 1][left][orders[i]], dp[i][left][right] + force(right, orders[i]))

# 테이블에서 최소 드는 힘 구하기
answer = 500001

for left in range(5):
    for right in range(5):
        answer = min(answer, dp[len(orders)-1][left][right])

# 결과 출력
print(answer)

• 결과