[파이썬/Python] 백준 1654번: 랜선 자르기

숨·2024년 7월 9일

코테

알고리즘 문제 풀이

목록 보기

21/105

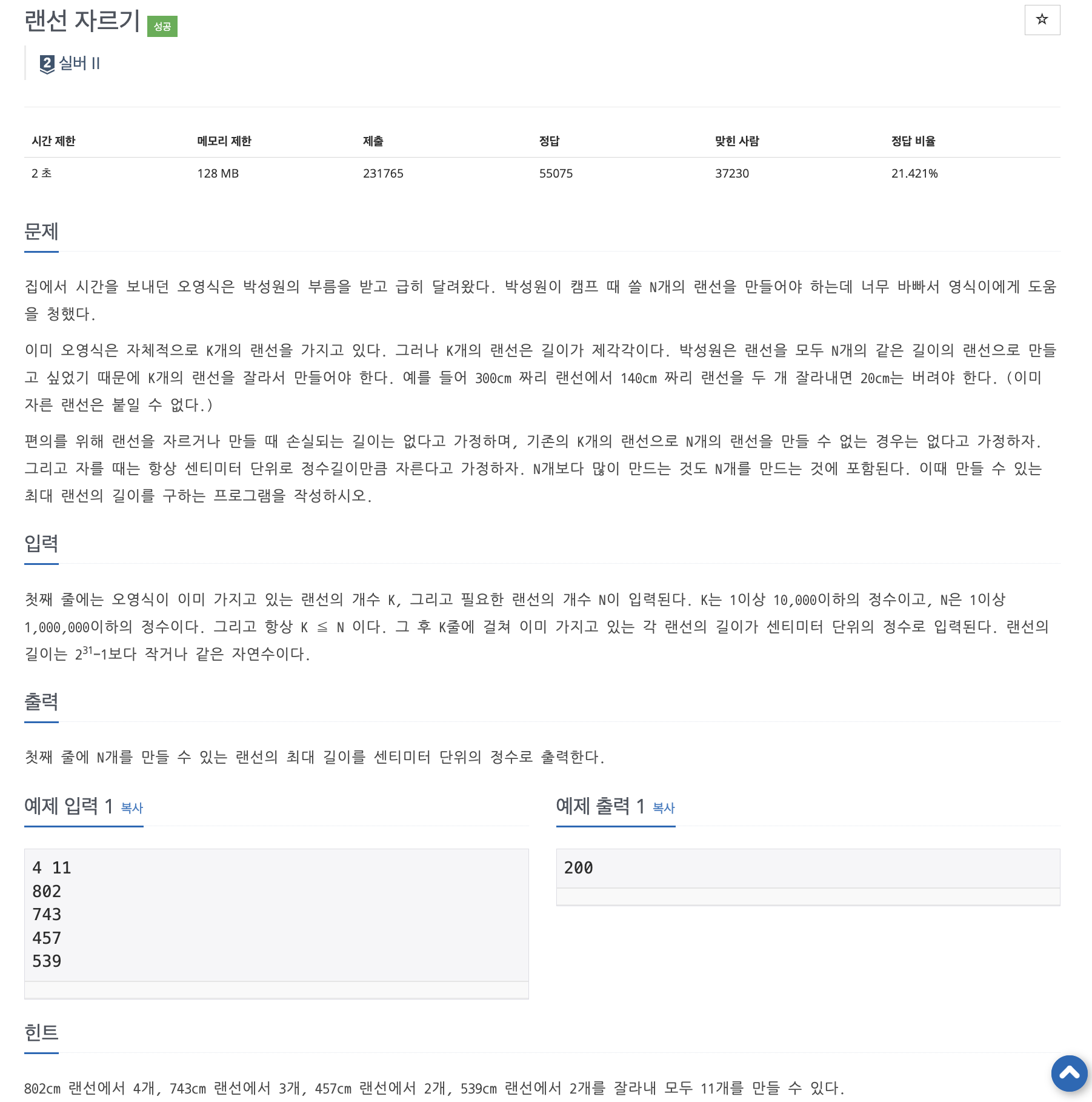
📌 문제 : 백준 1654번

📌 문제 탐색하기

K : 가지고 있는 랜선 길이 (1 ≤ K ≤ 10,000)
N : 필요한 랜선의 개수 (1 ≤ N ≤ 1,000,000)
→ 항상 K ≦ N

✅ 입력 조건
1. K, N 공백으로 구분해 입력
2. K개의 각 랜선의 길이 입력
✅ 출력 조건
1. N개를 만들 수 있는 랜선의 최대 길이를 센티미터 단위 정수로 출력

입력받은 랜선 길이들을 오름차순 정렬한다.

처음엔 랜선의 길이 중 가장 긴 길이와 가장 짧은 길이를 이용하려 했으나,
랜선의 길이에 비해 N이 매우 클 경우, 가장 짧은 길이보다 랜선의 최대 길이가 짧을 수 있다는 생각이 들었다.
따라서, 탐색할 범위를 K의 최소값인 1부터 최대 길이까지로 잡았다.

가장 긴 랜선과 1의 중간 길이를 구하고,
그 길이를 각 랜선 길이들에 나눠서 몫들의 합을 구한다.

그 합이 원하는 N과 일치하는지 확인한다.
N보다 크면 중간 길이에 +1한 것을 start로 갱신, N보다 작으면 중간 길이에 -1한 것을 end로 갱신한다.

위의 과정을 start ≤ end 될 때까지 진행하면, end는 가능한 최대 랜선의 길이가 된다.
이 end를 출력하면 된다.

위의 조건에 따라 이분탐색을 구현한다.

가능한 시간복잡도

K개 랜선 리스트 입력받기 → $O(K)$
K개 랜선 오름차순 정렬 → $O(KlogK)$
while문 내 이분 탐색 → $O(Klog(end-start))$

최종 시간복잡도
$O(KlogK)$ 으로 제한 시간 내에 연산이 가능하다.

알고리즘 선택

리스트의 각 요소들을 나눈 몫의 합이 N이 되도록 이분 탐색하는 방식

📌 코드 설계하기

K, N 입력
K번 반복해 길이 입력
랜선 길이 오름차순 정렬
이분 탐색 구현
4-1. start, end, mid 정의
4-2. 각 길이에 나누어 얻은 몫의 합 계산
4-3. 조건문에 따라 start, end 조절
원하는 형식으로 출력

📌 시도 회차 수정 사항

1회차

📌 정답 코드

import sys

input = sys.stdin.readline

# 1. K, N 입력
K, N = map(int, input().split())

# 2. K번 반복해 길이 입력
lengths = [int(input()) for _ in range(K)]

# 3. 랜선 길이 오름차순 정렬
lengths.sort()

# 4. 이분 탐색 구현
# 4-1. start, end 정의
start = 1
end = lengths[-1]

while start <= end:
    # 4-2. mid 정의
    mid = (start + end) // 2

    # 4-3. 각 길이에 나누어 얻은 몫의 합 계산
    count = 0
    for length in lengths:
        count += length // mid

    # 4-4. 조건문에 따라 start, end 조절
    if count >= N :
        start = mid + 1
    else:
        end = mid - 1

# 5. 원하는 형식으로 출력
print(end)