[파이썬/Python] 백준 18352번: 특정 거리의 도시 찾기

숨·2024년 8월 30일

알고리즘 문제 풀이

목록 보기

66/105

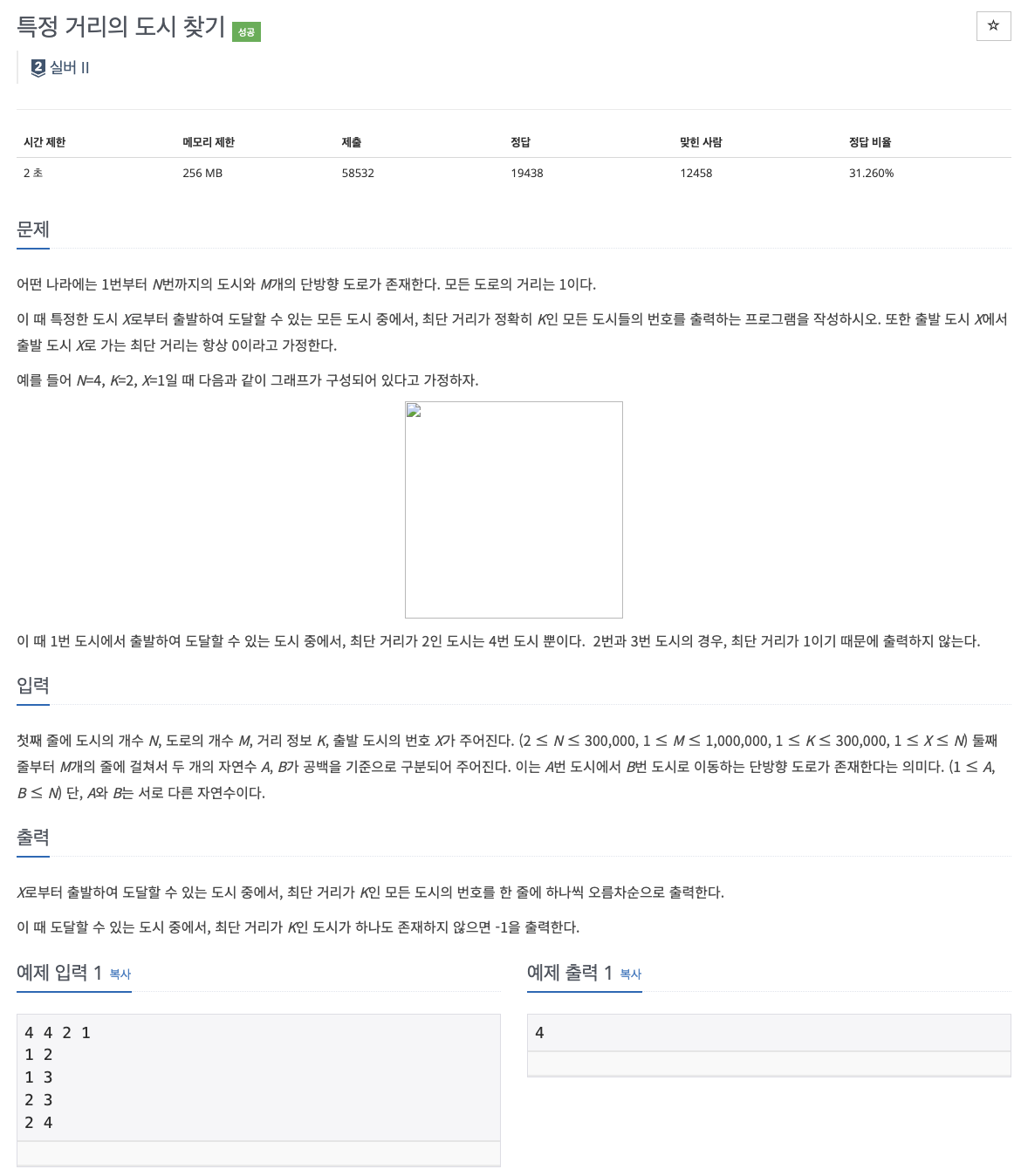
📌 문제 : 백준 18352번

📌 문제 탐색하기

N : 도시 개수 $(2 ≤ N ≤ 300,000)$
M : 도로 개수 $(1 ≤ M ≤ 1,000,000)$
K : 거리 정보 $(1 ≤ K ≤ 300,000)$
X : 출발 도시 번호 $(1 ≤ X ≤ N)$

M개의 A에서 B로 가는 도시 연결 정보를 입력 받아, 출발 도시 X로 부터 거리 K만큼 떨어져 있는 도시 번호를 오름차순으로 출력하는 문제이다.

문제 풀이

BFS를 이용해 시작 도시부터 연결된 도시들을 탐색하면서 이동 거리를 계산하고, 그 중 K의 거리를 가진 도시들을 찾아 출력하면 될 것이다.

도시 연결 정보를 저장할 그래프와 시작 도시 X로부터 각 도시까지의 이동 거리를 저장할 리스트를 정의한다.
입력받은 도시 연결 정보는 A에서 B로 가는 단방향 연결 정보이기 때문에 시작 도시에만 연결 정보를 저장한다.
시작 도시 X에서 BFS를 수행해 각 도시까지의 거리를 구한다.
도시를 탐색하면서 거리를 계산하는 BFS를 구현한다.
4-1. 자료구조 큐를 이용한다.
4-2. 해당 노드에서 연결된 모든 도시를 확인한다.
4-3. 방문하지 않은 도시라면 방문 처리한다.
4-4. 이동 거리를 이전 도시까지의 거리에서 1을 증가함으로써 거리를 계산한다.
4-5. 모든 도시를 방문할 때까지 탐색을 반복한다.

BFS로 구한 각 도시까지의 거리 중 K인 도시를 찾아 오름차순 정렬해 출력하면 된다.

가능한 시간복잡도

그래프 입력 → $O(M) = O(M)$
BFS 수행 → $O(N + M)$
도시 정렬 → $O(NlogN)$

최종 시간복잡도
$O(NlogN)$ 로 최악의 경우 $O(10^5 * log(10^5))$ 이 되어 2초 내 연산 가능하다.

알고리즘 선택

시작 노드부터 BFS 수행해 거리를 얻고 K 거리의 도시 번호 오름차순 정렬하기

📌 코드 설계하기

BFS 구현
N, M, K, X 입력
그래프 정의
연결 정보 입력
BFS 수행
거리 K인 도시 찾기
결과 출력

📌 시도 회차 수정 사항

1회차

📌 정답 코드

import sys
from collections import deque

input = sys.stdin.readline


def bfs(start):
    queue = deque([start])
    # 방문 리스트 정의
    visited = [0] * (N + 1)
    # 방문 처리
    visited[start] = 1
    # 이동 거리를 저장할 리스트 정의
    distance = [-1] * (N + 1)
    # 시작점 초기화
    distance[start] = 0

    while queue:
        v = queue.popleft()
        # 현재 도시에서 갈 수 있는 모든 도시 탐색
        for next_city in graph[v]:
            if not visited[next_city]:
                visited[next_city] = 1
                distance[next_city] = distance[v] + 1
                queue.append(next_city)

    return distance


# N, M, K, X 입력
N, M, K, X = map(int, input().split())

# 그래프 정의
graph = [[] for _ in range(N + 1)]


for _ in range(M):
    A, B = map(int, input().split())
    # 연결 정보 입력
    graph[A].append(B)

# bfs 수행
distances = bfs(X)

#  K의 거리를 가진 도시 찾기
cities = [i for i in range(1, N+1) if distances[i] == K]

# 결과 출력
if cities:
    for city in sorted(cities):
        print(city)
else:
    print(-1)