[파이썬/Python] 백준 1916번: 최소비용 구하기

숨·2024년 8월 31일

코테

알고리즘 문제 풀이

목록 보기

67/105

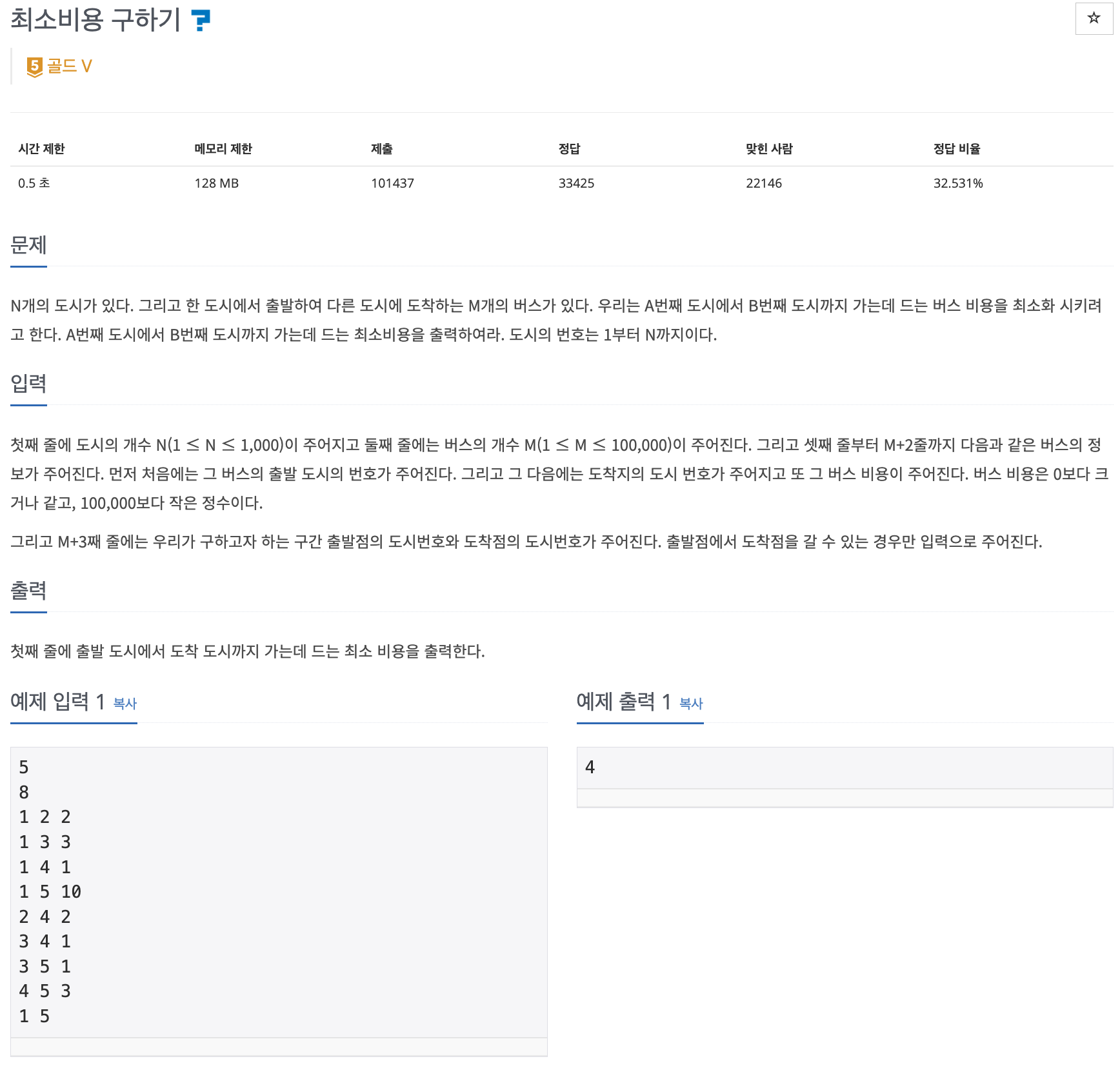
📌 문제 : 백준 1916번

📌 문제 탐색하기

N : 도시 개수 $(1 ≤ N ≤ 1,000)$
M : 버스 개수 $(1 ≤ M ≤ 100,000)$

도시 개수, 버스 개수를 입력 받고 출발 도시 번호, 도착 도시 번호, 버스 비용을 순서대로 입력 받는다.
알고 싶은 출발 도시, 도착 도시를 입력 받아 이동하는데 드는 최소 비용을 구하는 문제이다.

문제 풀이

출발 도시 번호, 도착 도시 번호, 버스 비용를 입력받기 때문에 버스 정보로 저장할 그래프는 가중치가 있는 단방향 그래프라고 할 수 있다.

다익스트라 알고리즘을 힙 자료구조를 사용한 우선순위 큐로 구현한다면 효율적으로 출발 노드에서 다른 모든 노드까지의 최단 거리를 구할 수 있다.

알고리즘의 결과로 얻은 최단 거리 중 도착 도시까지의 최단 거리를 출력하면 원하는 결과를 얻을 수 있을 것이다.

⭐️ 다익스트라 알고리즘 구현하기
1️⃣ 시작 도시의 최단 거리를 0으로 하고 큐에 삽입
2️⃣ 큐가 빌 때까지 거리가 가장 짧은 도시 선택
3️⃣ 해당 도시에서 갈 수 있는 모든 도시의 거리 계산
4️⃣ 최단 거리로 갱신하고 해당 도시를 큐에 삽입해 위의 과정 반복

가능한 시간복잡도

버스 정보 입력 → $O(M)$
각 도시 힙 연산 → $O(NlogN)$
연결 도시 힙 연산 → $O(MlogN)$

최종 시간복잡도
$O((N+M)logN)$ 으로 최악의 경우 $O(10^5 * log(10^3))$ 이 된다.
이는 0.5초내 연산 가능하다.

알고리즘 선택

다익스트라 알고리즘 이용

📌 코드 설계하기

필요한 입력 받기
버스 정보 저장할 그래프 정의
최단 거리 저장할 리스트 정의
다익스트라 구현
다익스트라 수행
결과 출력

📌 시도 회차 수정 사항

1회차

DFS/BFS 문제를 풀듯 방문 리스트를 따로 정의했다.
처음에 거리를 무한으로 정의해놓았고 이 거리는 최솟값을 갖도록 갱신되기 때문에 이 과정이 수행되었는지 아닌지만 확인한다면 굳이 방문 처리 리스트를 정의할 필요가 없게 되어 제거했다.

2회차

다익스트라 알고리즘을 이용하면서 최소 비용 = 최단 거리로 치환해서 코드를 작성하다가 똑같은 의미인데 변수명이 distance, weight로 달라지면서 비용 갱신하는 부분을 잘못 구현했다.

📌 정답 코드

import sys
import heapq

input = sys.stdin.readline

# 무한 의미
INF = int(1e9)

# N 입력
N = int(input())

# M 입력
M = int(input())

# 버스 정보 저장할 그래프 정의
graph = [[] for _ in range(N + 1)]

# 최단 거리 저장할 리스트 정의
distances = [INF] * (N + 1)

# M개의 버스 정보 입력
for _ in range(M):
    start, end, weight = map(int, input().split())
    # 단방향 그래프
    graph[start].append((end, weight))


# 다익스트라 구현하기
def dijkstra(start):
    queue = []
    # 시작 도시 최단 거리 0
    heapq.heappush(queue, (0, start))
    distances[start] = 0

    # 큐 빌 때까지 반복
    while queue:
        # 값이 가장 작은 도시 선택
        distance, city = heapq.heappop(queue)
        # 방문한 적 있는 도시면 무시
        if distances[city] < distance:
            continue

        # 연결 도시 확인
        for next_city, weight in graph[city]:
            new_distance = distance + weight

            # 더 짧은 거리 있으면 갱신
            if new_distance < distances[next_city]:
                distances[next_city] = new_distance
                heapq.heappush(queue, (new_distance, next_city))


# A, B 입력
A, B = map(int, input().split())

# 다익스트라 수행
dijkstra(A)

# B 최단 거리 출력
print(distances[B])

결과

📌 정리

👑 다익스트라 (dijkstra) 알고리즘

그래프에서 최단 거리 구하는 알고리즘
- 기능
  - 출발 노드 → 모든 노드 간 최단 거리 탐색
  - 결과로 얻은 리스트에서 모든 노드 간 최단 거리 확인 가능
- 특징
  - 에지 모두 양수
- 시간 복잡도 : $O(E log V)$
  - 노드 수 : V, 에지 수 : E

🐍 다익스트라 알고리즘의 5가지 단계

인접 리스트로 그래프 구현
1-1. N의 크기 클 것 대비해 인접 리스트 선택
1-2. input 데이터 자료형 형태 : (노드, 가중치)
최단 거리 리스트 초기화
2-1. 출발 노드 0, 이외 노드 무한으로 초기화
2-2. 무한 : 모든 에지의 합보다 충분히 더 큰 수로 정의
값이 가장 작은 노드 선택
3-1. 최단 거리 리스트에서 가장 값 작은 노드 선택
3-2. 값 0인 출발 노드에서 시작
최단 거리 리스트 업데이트
4-1. 연결된 에지 값 바탕으로 다른 노드 값 업데이트
4-2. 연결 노드의 최단 거리 : Min(선택 노드의 최단 거리 리스트 값 + 에지 가중치, 연결 노드 최단 거리 리스트 값)
3, 4단계 반복해 최단 거리 리스트 완성
5-1. 방문 리스트로 확인하면서 모든 노드를 방문할 때까지 반복

🐍 다익스트라 알고리즘 구현하는 2가지 방법

단계마다 방문하지 않은 노드 중 최단 거리 가장 짧은 노드 선택하기 위해 리스트의 모든 원소 확인(순차 탐색)하는 방법
- 시간 복잡도 : $O(V^2)$ / V: 노드의 개수
- 🚨 노드 개수가 10,000개 넘어가면 이용하기 어려움
힙 자료구조를 이용한 우선순위 큐로 구현하는 방법
- 시간 복잡도 : $O(NlogN)$
- 힙 자료구조
  - 우선순위 큐 구현 위해 사용하는 자료 구조 중 하나
  - 시간 복잡도
    - 삽입 → $O(logN)$ 를 N번 반복
      - 삭제 → $O(logN)$ 를 N번 반복
- 우선순위 큐(Priority Queue)
  - 우선순위가 가장 높은 데이터를 가장 먼저 삭제
    - 내부적으로 최소 힙(Min Heap) 또는 최대 힙(Max Heap) 이용
      - ⭐️ 최소 힙 → 값 낮은 데이터 먼저 삭제 (다익스트라에서 이용)
      - 최대 힙 → 값 큰 데이터 먼저 삭제
  - 더 빠르게 동작하는 heapq 사용 권장
  - 우선순위에 따라 데이터 처리하고 싶을 때 사용
    - (가치, 물건)으로 묶어 우선순위 큐에 넣기
      - 물건 꺼내면 항상 가치 높은 물건 먼저 나옴