주성분 분석

비지도학습은 입력 데이터에 대한 목표값 없이 학습시키는 머신러닝 방법이다. 주로 연관 있는 것들을 찾고 그룹핑하는 군집화방식을 이용한다.
머신러닝은 알고리즘을 사용하여 데이터에서 패턴을 찾는데, 학습 데이터에 특성의 수가 적으면 머신러닝 모델의 성능이 떨어지고, 특성의 수가 너무 많으면 알고리즘이 학습 데이터에 과대적합될 가능성이 있다. 따라서 차원을 축소한다는 것은 데이터의 중요한 특성은 남기고 불필요한 특성의 개수를 줄이는 것을 말한다.
차원을 축소하는 과정에서 정보가 유실될 가능성이 있기 때문에 정보 손실은 최소화하면서 원본 데이터를 저차원으로 다시 표현하는 것이 중요하다.

차원?
차원이란 데이터에서 변수를 말한다.
예를 들어 사람의 데이터에서 변수는 몸무게, 나이, 키 등이 될 수 있다. 즉, 속성의 개수를 의미하기도 한다.

차원축소 방법

차원을 축소하는 방법은 특성 선택과 특성 추출이 있다.
특성 선택은 훈련에 가장 유용한 특성을 선택하는 것
특성 추출은 기존 특성을 반영해서 저차원으로 중요 특성으로 압축하는 것이다.

주성분 분석은?

주성분 분석(PCA, Principal Component Analysis)은 데이터의 분산을 최대한 유지하면서 특성이 많은 데이터세트의 차원을 줄이는 방법이다.

일반적으로 주성분 분석 결과에서 누적 기여율이 80 ~ 90%를 차지하는 주성분들로 개수를 선택한다. 데이터를 표준화하고 기여율을 구한다음 높은 순서대로 정렬하면 추출해야할 특성들을 알 수 있다.

주성분 분석의 사용목적은 시각화와 시각화를 통한 데이터의 패턴 파악, 쓸모없는 특성을 줄이는 노이즈 제고, 복잡성을 줄이기 위한 데이터 전처리로 많이 활용한다.

실습

합성 데이터 생성하기

사이킷런의 라이브러리를 이용하면 임의의 데이터로 연습할 수 있다.
우리는 10차원의 특성과 5개의 군집을 이용할 것이다.

# 라이브러리 불러오기
# 합성 클러스트 데이터 셋 불러오기(샘플)
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

#실습용 데이터세트 생성
x,y = make_blobs(n_features=10, n_samples=1000,
                 centers=5, random_state=2023, cluster_std = 1)
#x는 2차원 배열 [1000][10]의 형태임, y는 1차원 배열의 형태이다.
# x의 첫번째 자료와 두번째 자료들을 x,y축으로 하여

plt.scatter(x[:,0], x[:,1], c = y)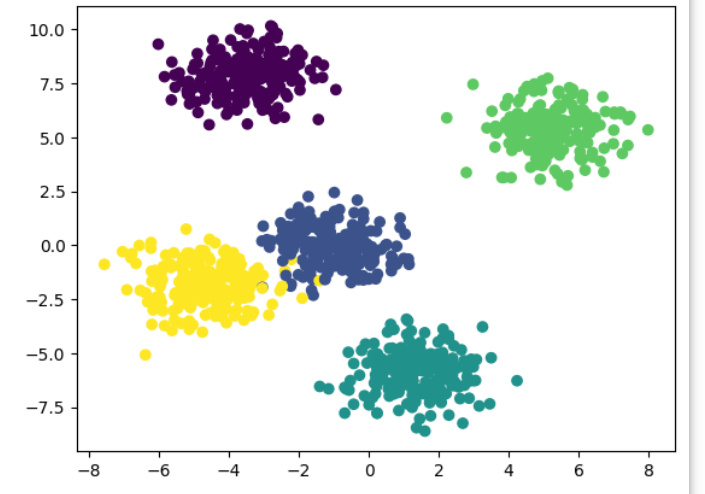

데이터세트 표준화하기

데이터의 분석의 오차를 줄이기 위해 데이터세트를 표준화한다.
변수 간의 스케일차이가 너무 크면 학습에 방해가 되며 이상치가 발생할 수 있다. 따라서 표준화를 통해 스케일을 줄여 이상치를 방지한다.

#데이터 세트 표준화하기
from sklearn.preprocessing import StandardScaler

#데이터 표준하기 
scaler = StandardScaler()
#  스케일러에 학습시킬 데이터 
scaler.fit(x)
# 표준화된 데이터 저장
std_data = scaler.transform(x)

주성분 분석 수행하기

코드를 작성하면 자동으로 추출해야할 주성분을 탐색해준다.
다음은 주성분 분석 함수를 통해 각 특성의 기여율과 누적기여율을 확인해보자

# 주성분 분석 수행하기 
import pandas as pd
from sklearn.decomposition import PCA
#PCA 객체로 주성분 10개 추출 / 원본의 주성분도 10이라 거의 의미는 없음
pca = PCA(n_components=10)
reduced_data = pca.fit_transform(std_data)
#주성분 확인용
pca_df = pd.DataFrame(reduced_data)

# 설명된 분산 값이 높은 순서대로 주성분 정렬
print(pca.explained_variance_)

#설명된 분산 비율 확인
print(pca.explained_variance_ratio_)

#설명력과 기여율을 확인하여 주성분을 추출
# 가시화를 위해 데이터프레임화 시켜서 도표로 보여준다.
import numpy as np
# 특성의 수 만큼 pca1 ~ pca10 만듦
index = np.array([f'pca{n+1}' for n in range(reduced_data.shape[1])])
# 생성된 인덱스를 이용하여 고유값과 기여율을 표현
result = pd.DataFrame({'고유값' : pca.explained_variance_, 
                       '기여율' : pca.explained_variance_ratio_}, index=index)
#누적기여율 추가
#1부터 10까지의 기여율을 모두 더하면 1이다.
result['누적기여율'] =  result['기여율'].cumsum()
#가시화된 도표
display(result)

#도표를 보고 아래와 같이 명시적으로 추출 할 수 있다. 
#PCA 객체로 주성분 4개 추출
pca = PCA(n_components=4)
X_reduced = pca.fit_transform(std_data)
print(pca.explained_variance_ratio_)

# 상위 주성분을 확인하고 추출하는 것보다 아래와 같이 비율을 작성하면 된다. 
pca = PCA(n_components=0.9)
reduced_data = pca.fit_transform(std_data)
print(pca.explained_variance_ratio_)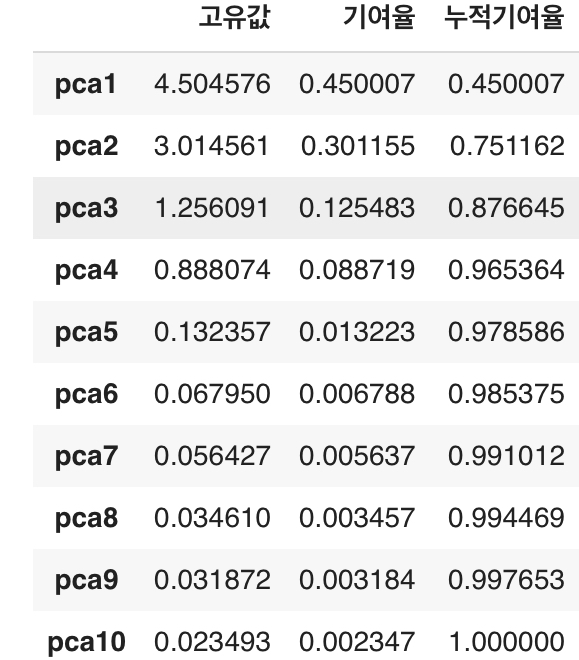

PCA 라이브러리로 비율을 입력하면 자동으로 누적기여율이 높은 순서대로 정렬해준다. 사용자는 추출된 주성분을 확인할 수 있게된다.