가설검증
가설검증
- 가설의 진실여부를 증명하는것
- 통계적 유의성을 검정하는 것으로 유의성 검정이라고도 한다.
- 모수에서 표본을 사용하여 진실여부를 True 혹은 False로 판단한다.
- 귀무가성이 사일이라고 가정하고 검증한다.
귀무가설
- 모집단의 표본의 평균(샘플평균)은 같다.
- 비교하는 값과 차이가 없다는 것은 기본 개념으로 설정하는 가설이다.
대립가설
- 모집단과 표본의 평균은 다르다.
- 대립가설은 단측가설과 양측가설로 분류된다.
| 구분 | 내용 |
|---|---|
| 귀무가설 |
기존에 알려진 사실이다. 일반적으로 진실이라고 믿고 있는 것 통계적 검정대상이 된다. (예: 모든 피고는 무죄이다.) |
| 대립가설 |
연구가설이라고 한다. 귀무가설과 대립하는 가설로 새로운 사실을 입증한다. 모수의 표본을 사용해서 검증한다. (예 : 모든 피고는 유죄이다.) |
가설검정의 종류
- 가설검정은 귀무가설을 채택할 것인지 기각할 것인지 검증한다.
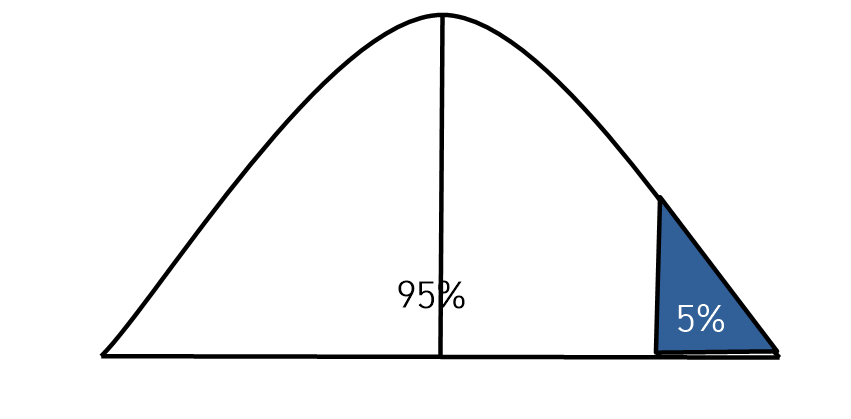
① 우측검정(Right-sided test)
- 전체 100%에서 오른쪽 5% 내에 있는지를 확인한다.
- 95%구간을 벗어나면 귀무가설은 기각된다.
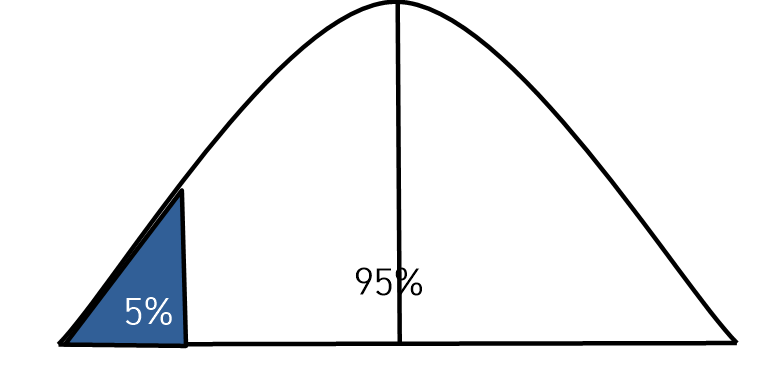
② 좌측검정(Left-sided test)
- 좌측 5%로 검정하여 귀무가설을 채택 또는 기각할 것인지 결정
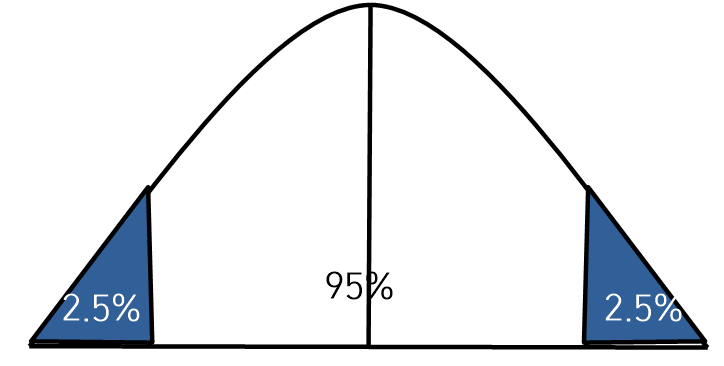
③ 양측검정(Two-sided test)
- 좌 우측 2.5% 구간을 기준으로 귀무가설을 채택할지 기각할지 결정
가설검증의 절차
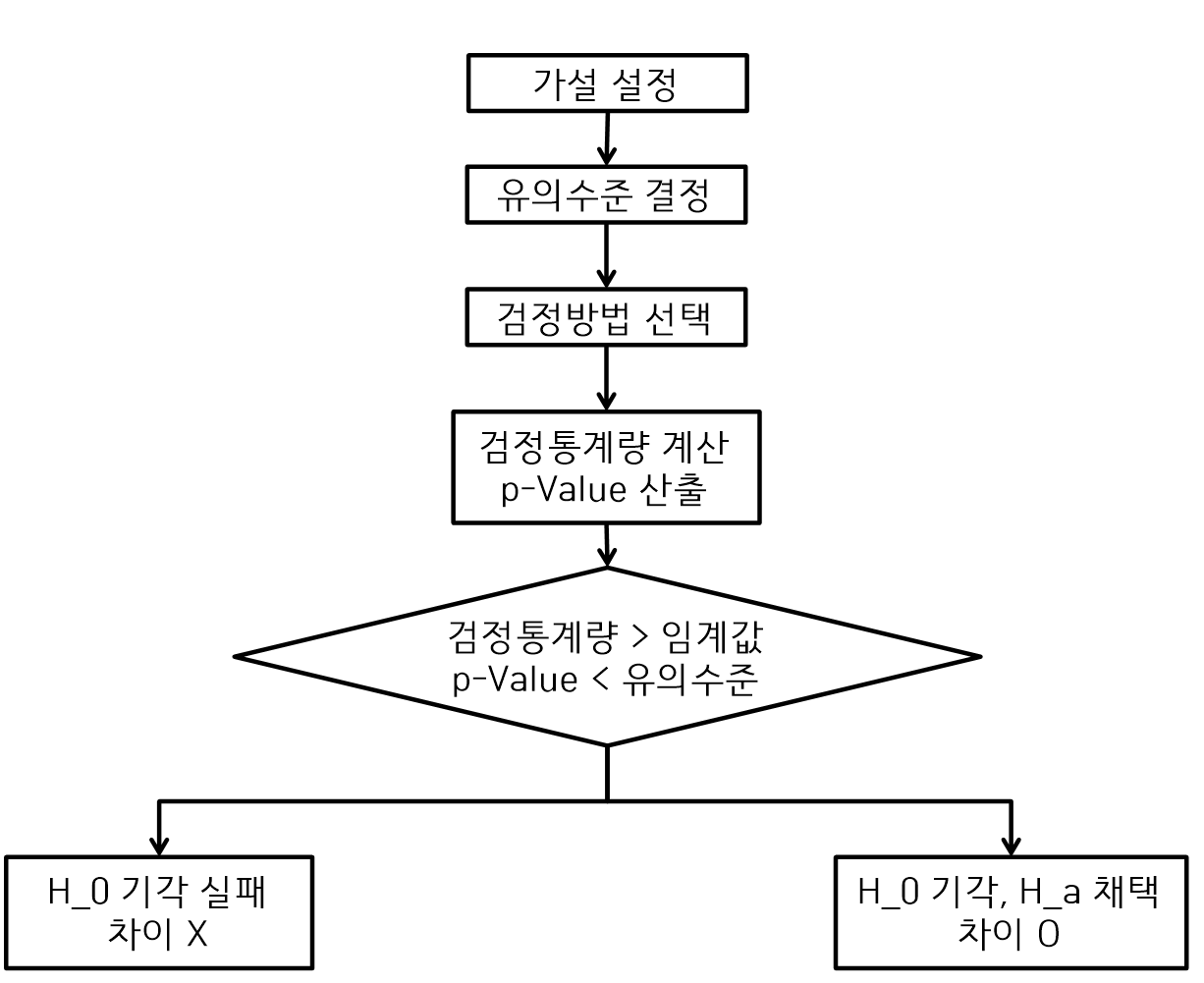
1) 귀무가설과 대립가설 설정
- 귀무가설을 설정하고 우측검정, 좌측검정, 양측검정을 수행
2) 유의수준 설정 - 0.05(5%)의 우의수준을 설정한다.
3) 검정방법 선택 - 통계적분석 방법을 설정한다.
4) 검정 통계량 계산 - 검정 통계량과 유의확률(p-Value)를 계산한다.
5) 통계적인 의사결정 - 비즈니스적으로 의사결정한다.
검정 통계량
- 검정통계량은 표본 데이터에서 계산되어 가설검정에 사용되는 랜덤변수이다.
- 귀무가설의 기각 및 채택여부를 판단할 수가 있다.
- 통계적 가설검정을 위해서 확률부노를 결정하는데 사용되는 통계량이다ㅣ.
- 검정 통계량은 Z분포, F분포, X제곱분포 등의 확률분포가 있다.
가설검증 오류
1종 오류(; 알파)
- 귀무가설()이 진실인데 귀무가설()을 기각하는 오류이다.
2종 오류(; 베타)
- 귀무가설()이 거짓인데 귀무가설()을 채택할 수 있는 오류이다.
1종오류와 2종오류
| 오류 | 위험 | 내용 |
|---|---|---|
| 1종 오류 | 알파위험 (α 위험) | 잘못된 부정적 의견을 표명하는 오류 기각 오류이다. 과소 신뢰의 오류이다. |
| 2종 오류 | 베타위험 (β 위험) |
잘못된 적정 의견을 표명하는 오류 채택 오류이다. 과대 신뢰의 오류 |
귀무가설과 대립가설 오류
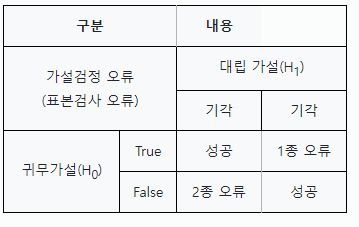
유의확률
- p-Value값이 5%보다 작으면 귀무가설은 기각되고 5%보다 크면 귀무가설은 채택된다.
- 귀무가설이 진실이라는 가정에서 표본 통계량의 값이 나타내는 확률이다.
- 95%의 신뢰도를 기준으로 가설판단에 사용된다.
- 0 ~ 1사이의 값을 가지고 있고 p 값은 전체 표본에서 하나의 표본이 나올 수 있는 확률이다.
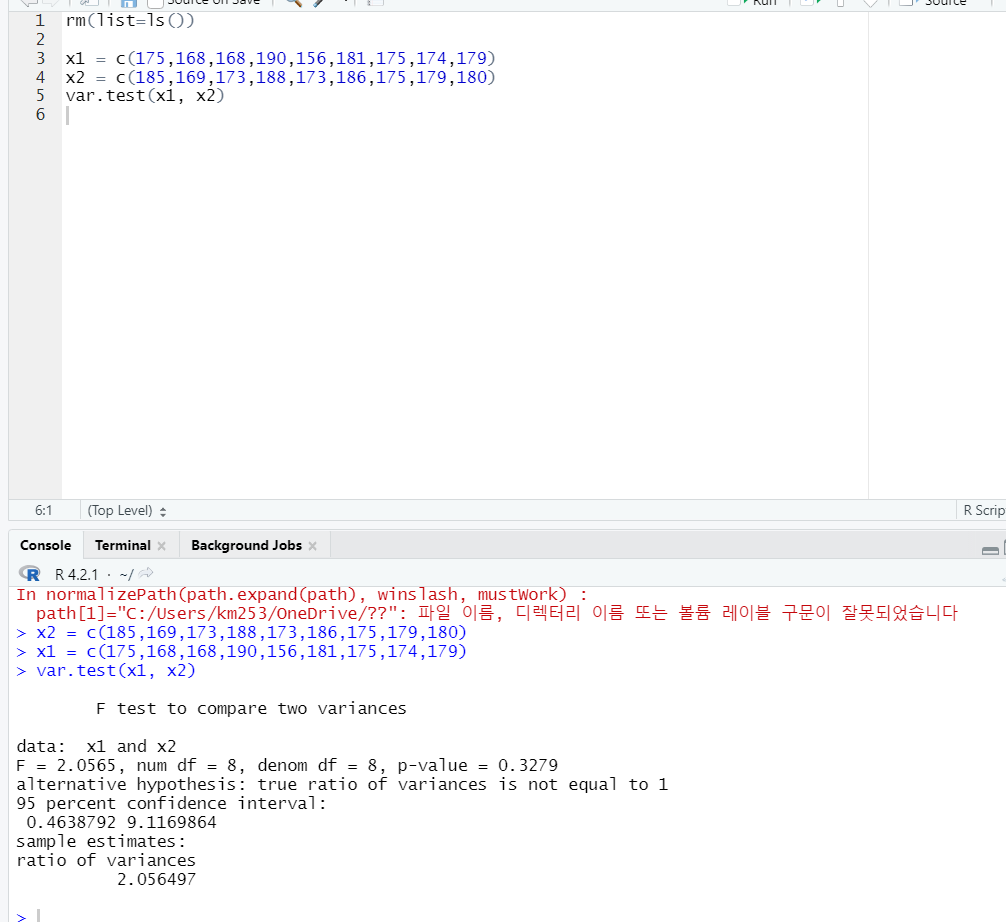
위 그림의 콘솔창을 보면 p-Value가 0.3279로 0.05보다 크기 때문에 귀무가설은 채택된다.
검정통계량
- 귀무가설이 참이라는 가정에서 얻은 통계량이다.
- Z-통계량 혹은 T-통계량이 널리 사용된다.
검정통계량 =
- 표본의 평균이 185이고 표준편차가 5일때 검정통계량은 2이다.
- (185-175)/5 = 2
- 여기서 175라는 것은 귀무가설로 정의된 평균 값이다.
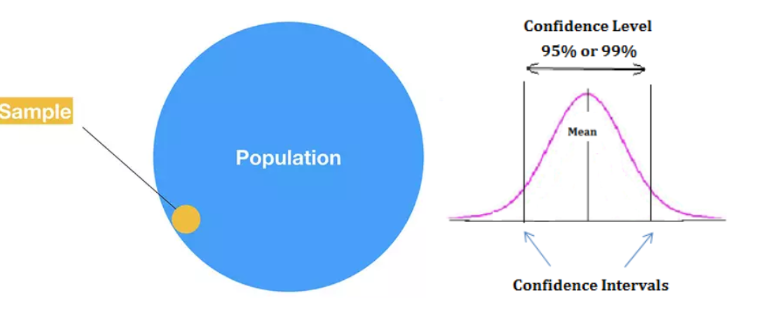
신뢰구간
신뢰구간
- 신뢰구간이란, 표본 통계량에서 파생되어서 알 수 없는 모집단 모수값이 포함될 값의 범위이다.
- 표본을 랜덤하게 추출하는 특성으로 인해서 특정 모집단의 두 표본은 동일한 신뢰구간이 될 수가 없다.
- 신뢰구준이란, 실제 모수를 추정하는데 몇 퍼센트의 확률로 신뢰구간이 실제 모수를 포함하게 되는가에 대한 것이다.
- 100개 중에서 95개가 모평균에 포함되면 신뢰구간을 95%라고 한다.
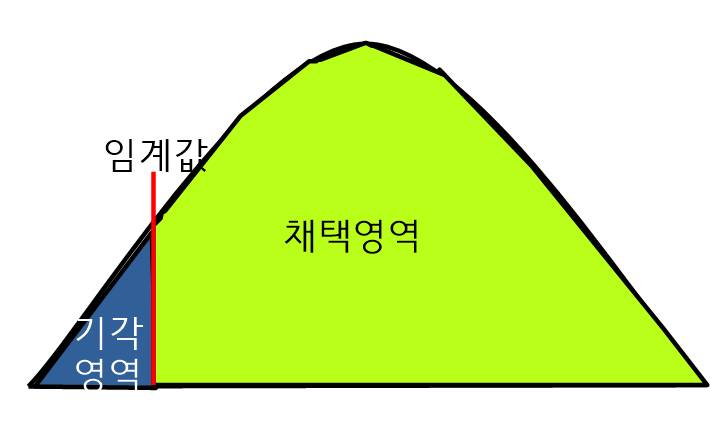
- 우측 정규분포에서 95%의 구간을 귀무가설 구간이라고 하며 여기에 해당하는 함수가 높은 신뢰도가 있다. 해당되지 못한 각각의 영역은 대립가설구간으로 유의수준이다.
- 대립가설이 채택되는 경우는 p-Value가 유의수준(0.05)보다 작으면 대립가설이 채택된다.
