ADsP -통계분석 기법

이강민·2022년 10월 12일
0

ADsP

목록 보기
14/19
post-thumbnail

통계분석 기법

통계분석

  • 통계분석이란 특정집단을 대상으로 자료를 수집하여 대상집단의 정보를 구해서 통계분석 기법으로 통계적 추론을 하는 일련의 과정을 의미한다.
  • 통계분석기법은 차이검정과 관계검정이 있다.

차이검정

  • 차이검점이란 여러 그룹 간의 차이를 비교하는 분석기법으로 평균과 분산의 차이를 분석한다.

평균차이검정

  • 어떤 집단간에 평균차이를 검정하는 것으로 질적변수 1개와 연속변수 1개를 분석한다.
  • 질적변수 1개는 집단을 구분하고 연속변수 1개는 평균을 계산한다.

평균검정(T-test)

  • 평균검정은 분석해야 하는 집단의 수가 2개 미만일 때 사용하는 방법이다.
  • 평균검정은 집단 간에 평균 값을 비교하는 분석기법으로 1종오류가 발생할 수 있다.
    • 1종오류 : 귀무가설이 진실인데 귀무가설을 기각하는 오류
    • 3개의 집단에 대해서 평균분석을 하면 1종 오류가 발생할 가능성이 높아진다.
    • 따라서 평균검점은 2개 집단에 대해서 분석한다.
  • 평균검정은 집단이 1,2,3이면, 1:2,2:3,1:3처럼 3번 평균을 비교하지만 분산분석은 한번에 평균을 비교한다.

평균검점의 종류

  • One Sample T-test
    • 하나의 집단에 평균이 얼마인지 검사하는 방법
  • Independent Samples T-test
    • 독립된 두 집단 간에 평균의 차이를 검사하는 방법
  • Paired Samples T-test
    • 하나의 집단을 처리 전과 처리 후로 나누어 분석하는 방법

One Sample T-test

  • 하나의 집단의 평균이 얼마인지 검사하는방법
  • ex) 질적변수는 남자이고 연속변수는 몸무게이다. 남자의 평균 몸무게를 분석하는 것

Independent Samples T-test

  • 독립된 두 개의 질적변수를 사용해서 A기업과 B기업의 평균 근무시간을 부석
  • 변수는 그룹으로 분류되고 그룹 간의 차이를 평균으로 계산한다.
  • 범주형 변수 한 개와 연속형 변수 하나를 사용해서 분석한다.'
  • ex) 범주형 변수는 도심내부, 도심외각으로 분류되고 연속형 변수는 학생들의 성적으로 분석
R에서의 분석
grade <- read.csv(file = "C:\\Users\\km253\\OneDrive\\바탕 화면\\Rlanguae\\test.txt",
                  header = TRUE, sep = " ")
attach(grade)
head(grade)
dim(grade)


내부 데이터를 확인한다.

grade <- read.csv(file = "C:\\Users\\km253\\OneDrive\\바탕 화면\\Rlanguae\\test.txt",
                  header = TRUE, sep = " ")

attach(grade)
head(grade)
dim(grade)
summary(grade)


중심값과 평균, 최소, 최대값을 알 수 있다.

t.test(성적~거주지, data = grade)


p-Value의 값이 0.05보다 작으므로 귀무가설은 기각하고 대립가설이 채택된다.
상자그림으로 표현하면 다음과 같다.

par(mfrow = c(1,1))
boxplot(성적~거주지, boxwex=0.5, col=c("yellow", "red"))


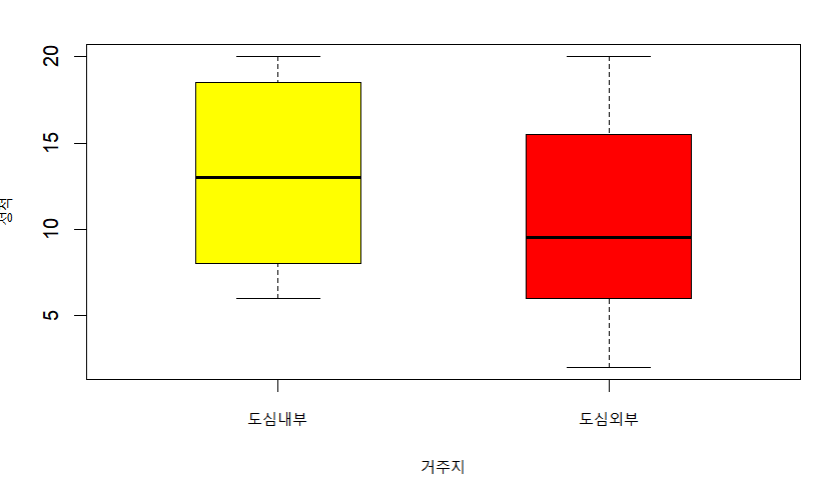
도심내부의 사는 학생의 성적이 더 높다.

Paired Samples T-test

  • 집단을 전과 후로 구분해서 지출하는 평균 생활비를 분석한다. 즉 짝을 이루는 변수를 전후에 분류해서 분석한다.
  • 특정 집단의 효과를 분석하기 위해서 사용한다.
독립표본과 대응표본의 차이

  • 독립표본(좌측)
    • 그룹으로 분류하고 그룹의 평균을 계산한다.
    • 그룹간의 평균을 비교한다.
  • 대응표본(우측)
    • 동일한 대상을 두 번 반복해서 측정
R로 보기


관측지와 변수의 갯수를 확인한다.

bp1 <- read.csv(file = "C:\\Users\\km253\\OneDrive\\바탕 화면\\Rlanguae\\pair.csv")
attach(bp1)
head(bp1)
dim(bp1)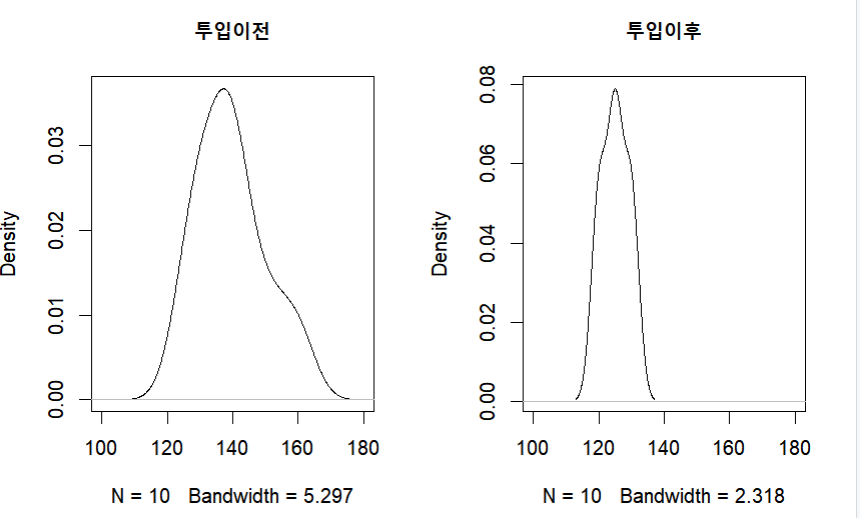


2개의 그래프를 그려서 비교할 준비를 한다.

par(mfrow=c(1,2))
plot(density(before), xlim=c(100,180), main="투입이전")
plot(density(after), xlim=c(100,180), main="투입이후")

t.test(before, after, mu=0, alternative = "greater", paired = T)

p-value가 0.5를 기준으로 너무 작은 값이 나왔으므로 귀무가설은 기각 되고 대립가설이 채택된다. 결론적으로 신약 투입 후에 혈압에 효과가 있다는 것이 채택된다.

분산분석(ANOVA, Analysis of Variance)

  • ANOVA는 전체분산을 여러 개로 분할하여 분석하는 것으로 어떤 요인의 영향이 유의한지를 검정한다.
  • 분산분석은 분석 데이터에서 집단이 3개 이상일 경우 사용한다.
  • 분산분석은 두 개 이상의 집단을 비교할 때 사용하며 각 집단의 평균 차이에 의해서 발생되는 집단 간의 분산을 비교한다.
  • F분포를 사용해서 가설을 검증하는 방법이다.

One way ANOVA

  • 종속변수 한 개와 독립변수 한개로 이루어진 데이터에서 사용하는 것으로 종속변수는 집단으로 분류되어 있는 경우에 사용한다.
  • One way ANOVA는 하나의 변수에 그룹이 3개 이상으로 되어 있어야 한다.
  • 다음의 예에서 지점 위치(변수)는 노원, 중구, 강남으로 구분되고 각 지점의 위치가 매출에 영향을 주는지 분석한다.
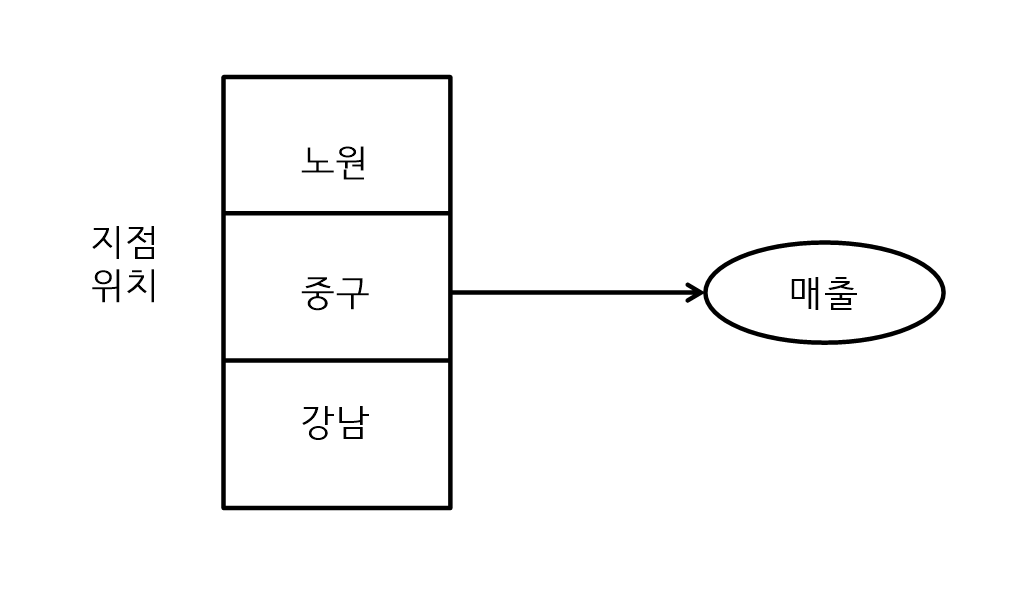
  • R프로그래밍에서 ANOVA 분석을 하려면 aov 함수를 사용, aov함수의 첫번째 파라미터에는 종속변수가 온다. 그리고 독립변수를 지정한다.
aov(종속변수~factor1+factor2)
  • aov함수를 사용할 때 One way ANOVA에서는 독립변수를 한 개로 지정하고 Two way ANOVA에서는 독립변수를 두 개 지정한다.

Two way ANOVA

  • Two way ANOVA는 독립변수가 두 개 이상인 경우 집단 간의 차이를 분석하여 유의성을 확인한다.

  • 평균 반응 프로파일을 사용하여 두 개의 변수 간에 상호작용을 확인하는 것

  • 다음의 예는 지점위치와 온도라는 두 개의 독립변수를 가지로 있고 각 독립변수는 각각 3개의 집단으로 분류되어 있다. 종속변수는 매출이며 지점위치와 온도가 매출에 어떤 영향을 주는지 분석하는 것이다.

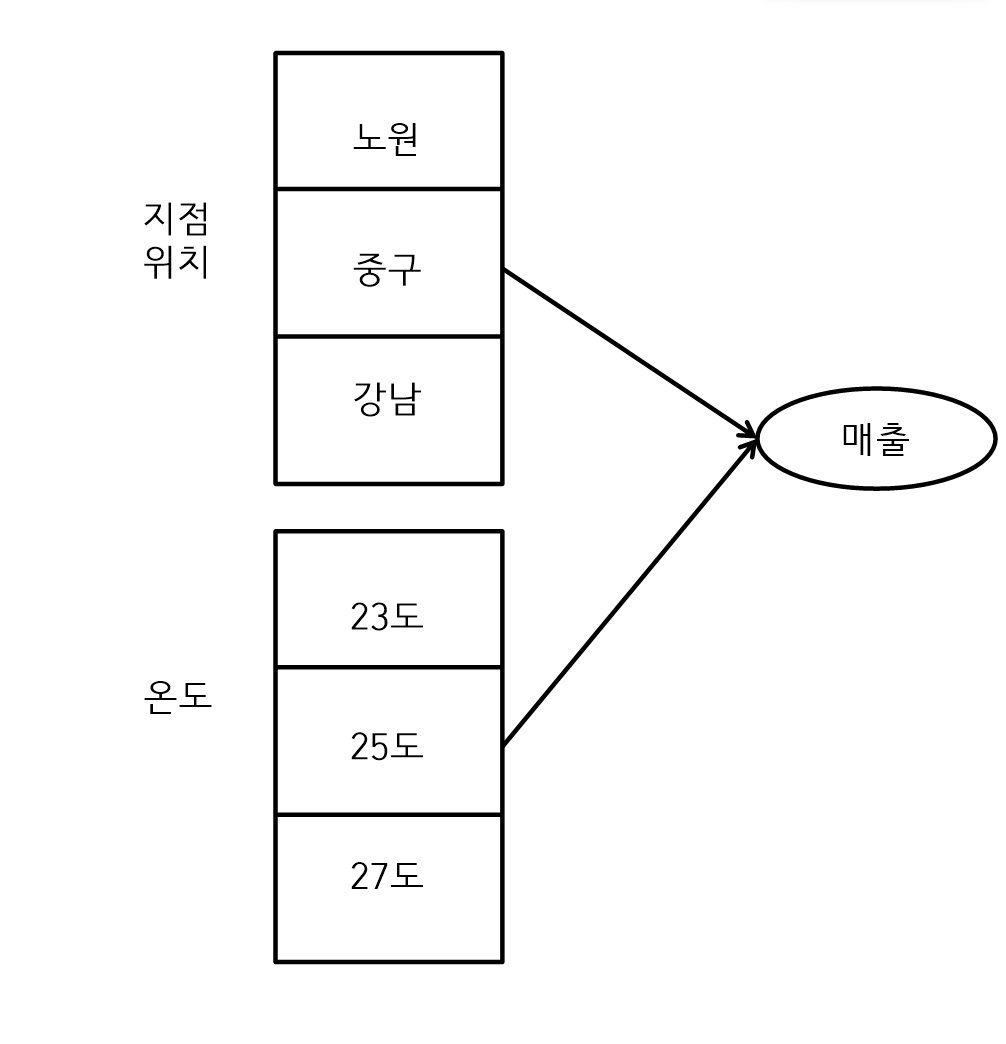
  • 상호작용이 없는 경우

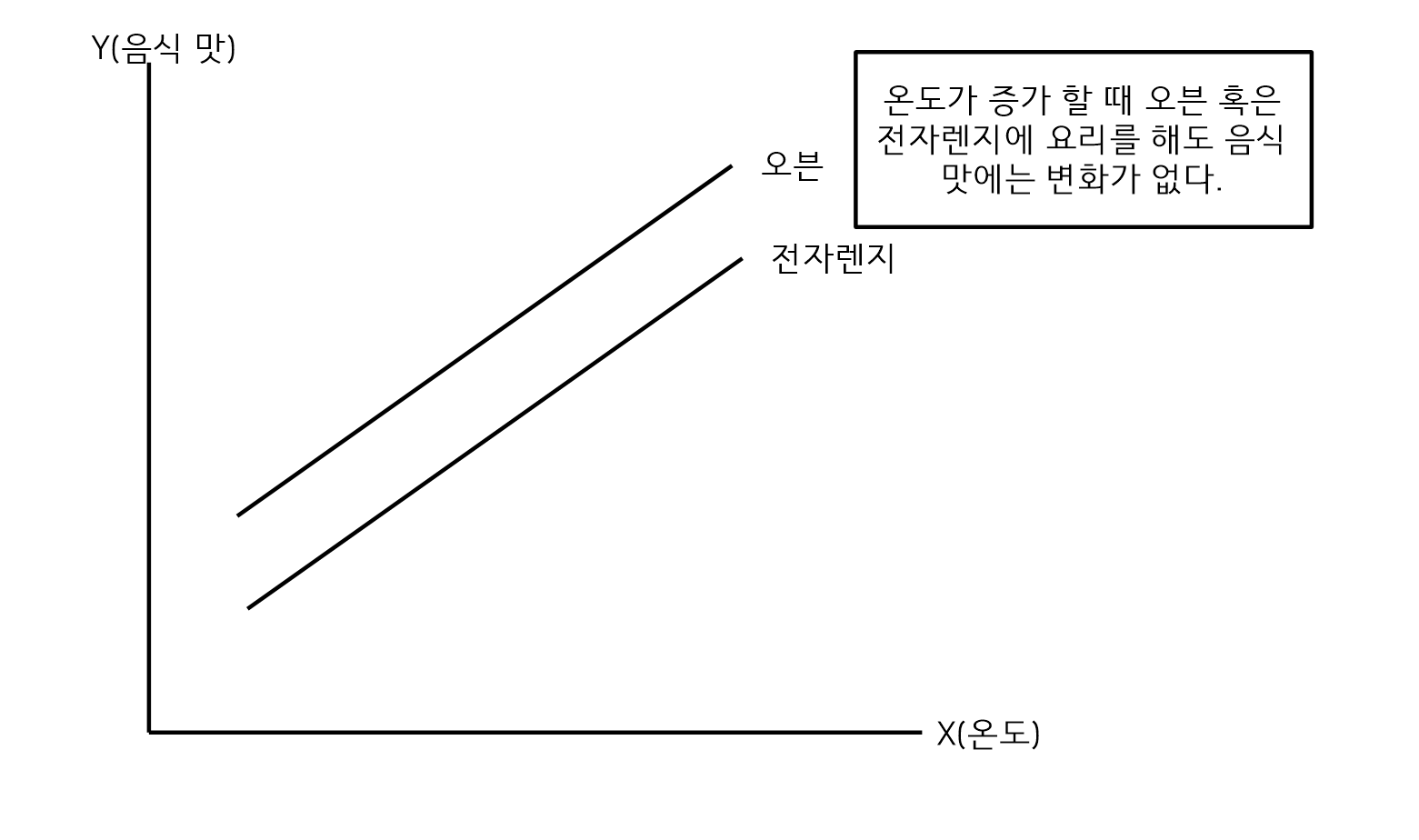
  • 상호작용이 없는 경우로 온도가 증가 해도 오븐과 전자레지로 요리하는 음식의 맛에는 상호작용이 없다.

  • 상호작용이 있는 경우

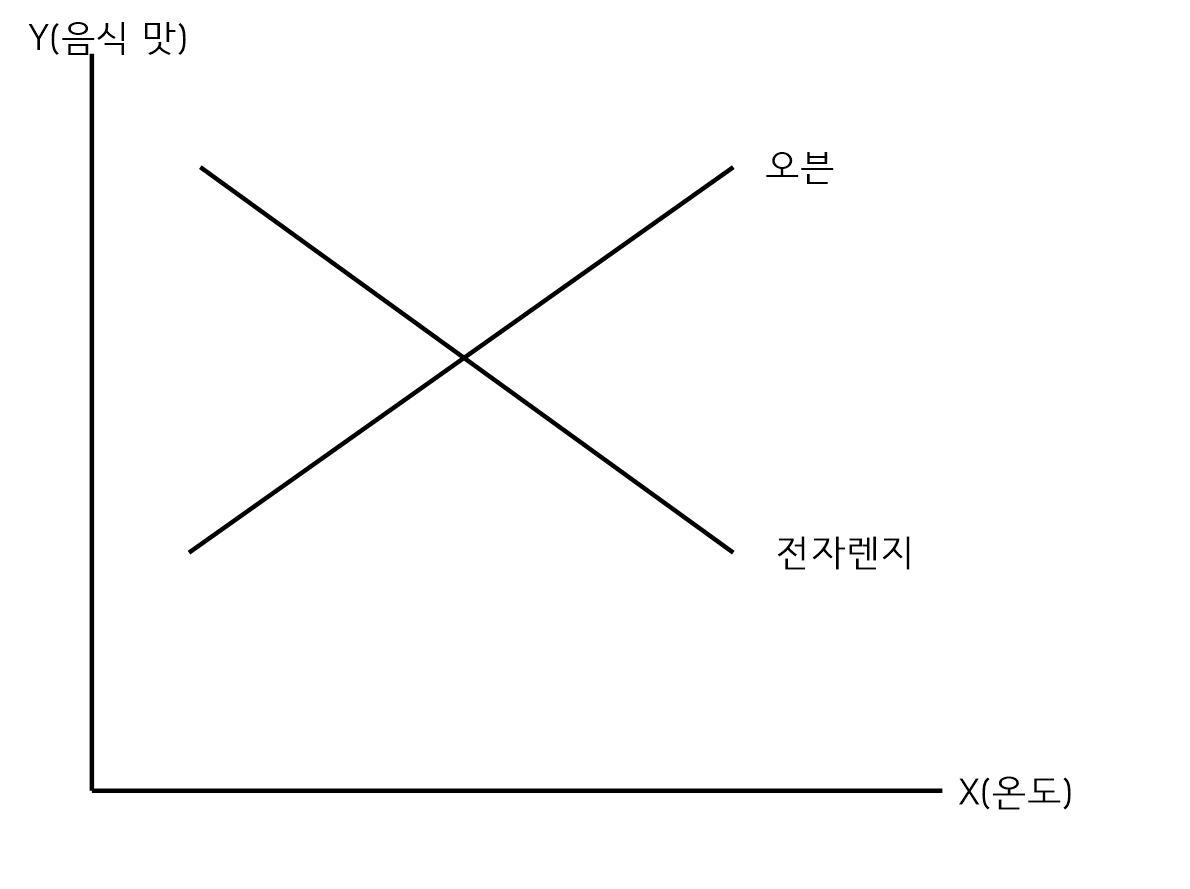
  • 온도가 증가하면 오븐으로 요리한 것과 전자렌지로 요리한 것이 음식 맛에 영향을 주므로 상호작용이 발생한다.

Repeated Measured ANOVA

  • Repeated Measured ANOVA는 시점 데이터를 사용해서 전과 후로 분석한다.
  • 시점으로 3개월 전, 3개월 후, 6개월 후로 학생들의 점수를 분석한다.
  • 반복해서 측정하여 변화된 것을 비교하는 방법이다.

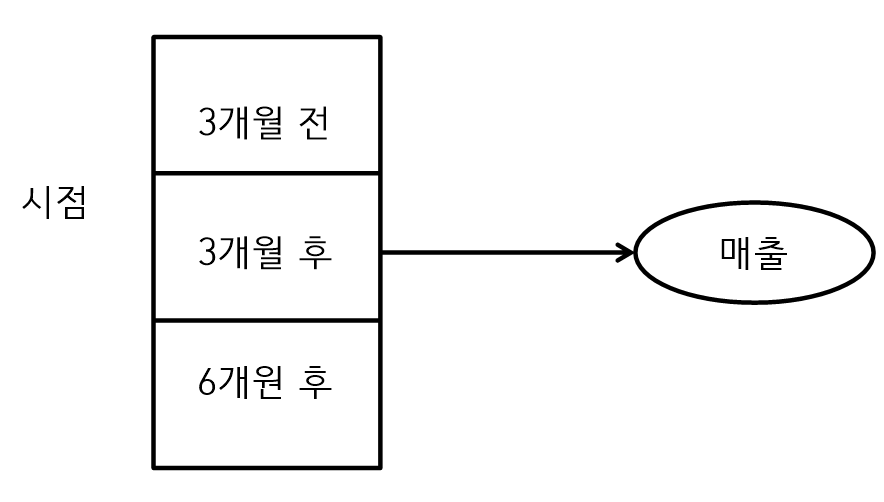
  • Two way Reapeated Measured ANOVA는 시점 데이터와 집단 데이터를 사용해서 분석하는 형태

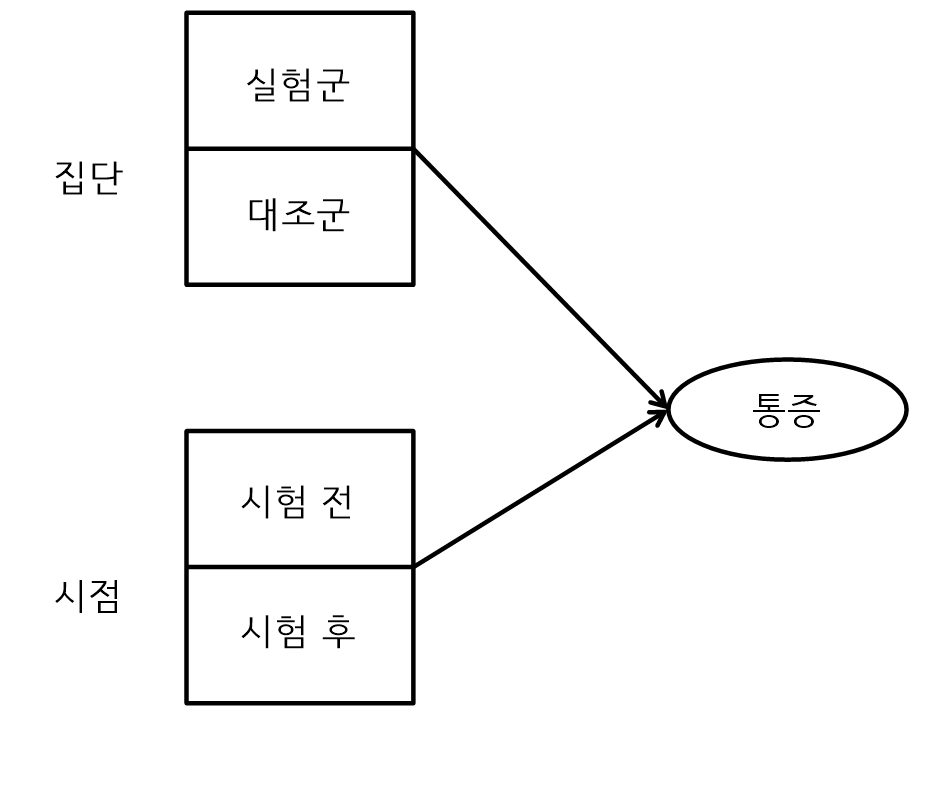
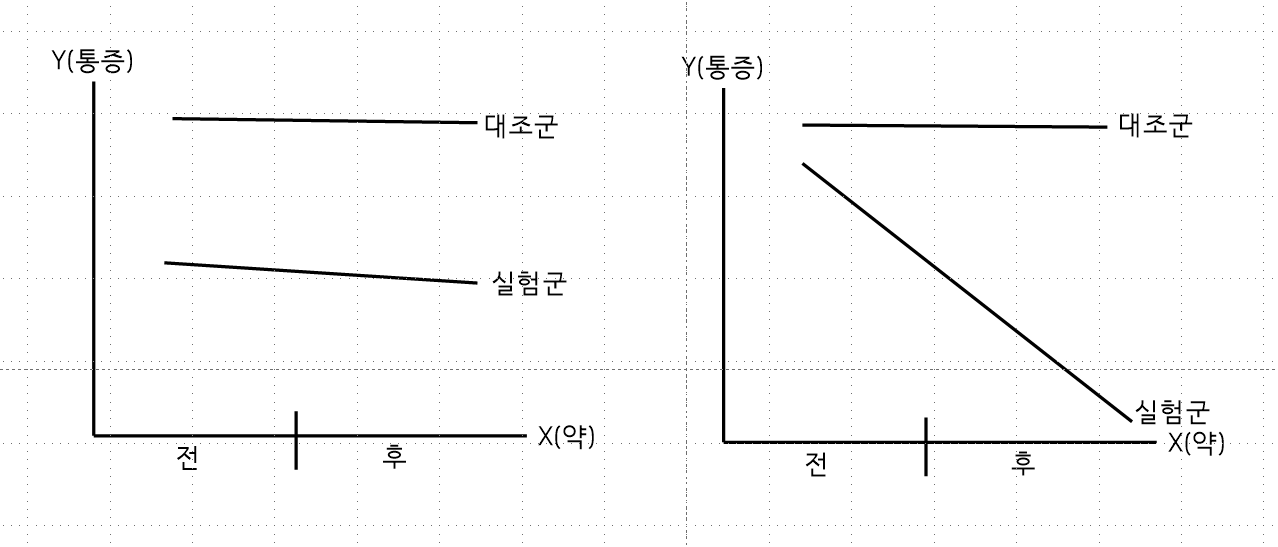
Two way Reapeated Measured ANOVA 예시

  • 상호작용이 없는 경우(좌)와 상호작용이 있는 경우(우)

관계검정

관계검정

  • 관계검정은 교차분석, 상관분석, 회귀분석이 있다.
  • 관계검정 기법
    • 상관분석 : 연속변수와 연속변수를 분석
    • 회귀분석 : 연속변수와 연속변수를 분석
    • 교차분석 : 질적변수와 질적변수를 분석

질적변수

  • 변수의 값이 자료를 특정 카테고리에 포함시키도록 하는 변수를 의미한다.
    • 성별, 종교 등

상관분석

  • 두 개의 변수 간에 관계를 통계적 기법으로 분석하는 행위로 변수 간에 인과관계가 명확하지 않을 때 사용한다. 즉, 두 변수가 균등관계인 경우 분석하는 것이다.
  • 상광관계는 선형관계를 전제로 하고 있다.
  • 두 변수 간에 강한 관련성을 가지고 있는 경우 다른 변수를 예측한다.
  • 균등관계란 예를 들어 키와 몸무게의 변수로 어떤 변수가 원인이고 어떤 변수가 결과인지 알 수 없을 때 변수는 균등관계에 있다라고 한다.

상관분석과 회귀분석의 비교

상관분석 회귀분석
두 변수가 어떤 관계가 있지만 인과관계를 알지 못할 경우 독립변수가 종속변수에 미치는 영향을 확인하는 분석 기법
분산을 분석 종속변수와 관련있는 독립변수를 찾거나 독립변수들 간 관계를 이해할 때 사용
데이터가 얼마만큼 밀접하게 모여 있는지를 분석 기울기를 분석, 독립변수 X의 변화에 따른 Y의 변화를 분석한다.

상관분석 예제

  • 야구선수의 타율과 연봉의 관계
    • 귀무가설 : 야구선수의 타율은 연봉에 관계가 없다.
  • 교육비용과 성적의 관계
    • 귀무가설 : 교육비용은 성적과 관계가 없다.

공분산

  • 두 변수 간에 분산을 공유하는 것, 두 변수가 공통분산을 사용
  • ex) 학생수의 분산과 성적의 분산을 공유하는 것. 즉, x의 분산과 y의 분산을 공유하는 것
  • 공분산은 척도 단위에 민감성이 크기 때문에 표준화를 수행한다.
  • 척도 단위라는 것은 예로 서울~부산까지 거리와 서울~유럽까지 거리 값의 척도는 차이가 있다.
    이를 표준화 시켜주어야 한다.
  • 표준화 시킨다는 것은 그 값이 0에서 1사이의 값을 가진다는 의미

상관계수

두 변수의 관계를 하나의 수치로 나타내는 척도, r로 표현하고 r은 강도, 방향으로 계산한다.

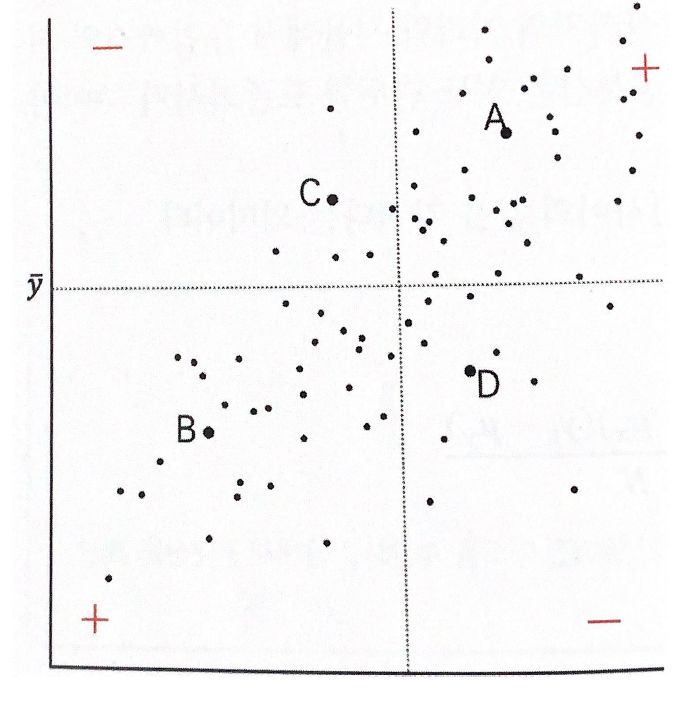
  • 평균과의 관계

  • 1사분면의 점(A)의 경우 X,Y 값이 둘다 평균보다 크다. x편차와 y편차가 둘 다 양수가 되므로, 편차의 곱도 양수가 된다.

  • 3사분면의 점(B)의 경우, X,Y 값이 둘다 평균보다 작다. 다시말해 x편차와 y편차가 둘 다 음수가 되므로, 편차의 곱은 양수가 된다.

  • 2사분면의 점(C)의 경우, X 값은 평균보다 작고 Y의 값은 평균보다 크다. x편차는 음수이고 y편차는 양수이므로, 편차의 곱은 음수가 된다.

  • 4사분면의 점(D)의 경우, X값은 평균보다 크고 Y의 값은 평균보다 작다. x편차는 양수이고 y편차는 음수이므로, 편차의 곱은 음수가 된다.

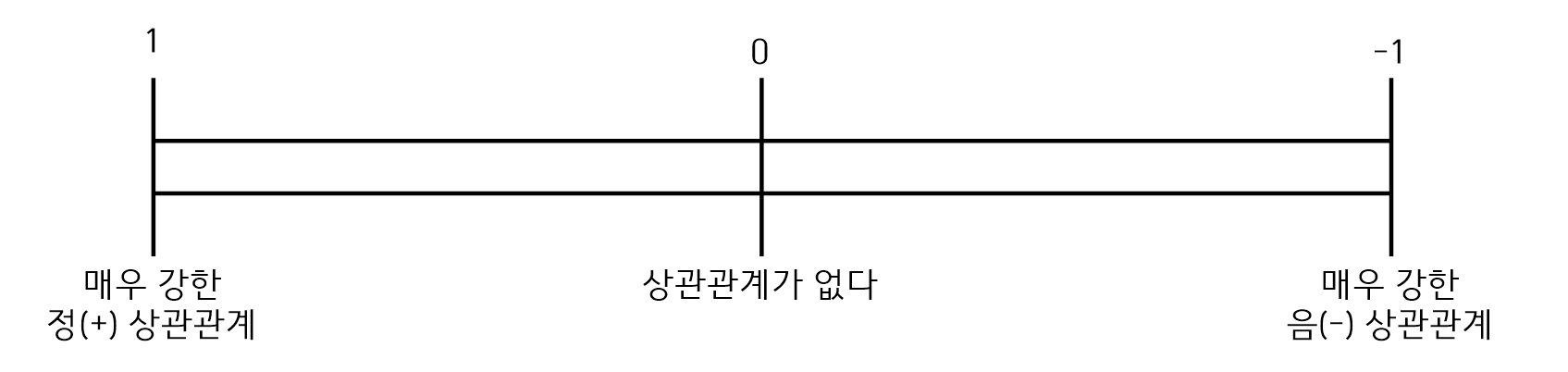
  • 상관계수의 해석은 1~-1의 값으로 해석된다. 상관계수 r이 0이면 두 변수 간의 상관관계가 없는 것이고 1쪽 혹은 -1쪽으로 값이 나타날수록 상관관계가 높은 것이다.

  • 상관계수가 1에 가까우면 양의 관계이고, -1에 가까우면 음의 관계이다.

상관계수의 검정

가설 상관관계
귀무가설(H0) 두 변수간의 상관관계가 없다.
H0:r = 0
대립가설(H1) 두 변수간의 상관관계가 있다.
H0:r <> 0

R에서의 상관분석해보기

  • 귀무가설 정의
    • H0H_0 : 학교까지의 거리는 학생들의 성적에 영향이 없다.
  • 거리와 성적 데이터는 R에 x1 변수와 x2 변수를 정의해서 임의의 값을 넣었다.
x1 <- c(10,1,5,2,4,6,1,3,8)
x2 <- c(82,94,88,90,87,84,91,87,83)
cor(x1, x2)
plot(x1,x2, main = "상관관계 테스트")
abline(lm(x2~x1), col="red", lwd=2, lty=1)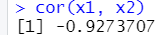

  • cor 함수를 이용해서 상관계수를 구한다.

  • -0.92737로 -1에 가까움으로 강한 음의 관계를 가진다.

  • 산점도를 그려보면 다음과 같다.

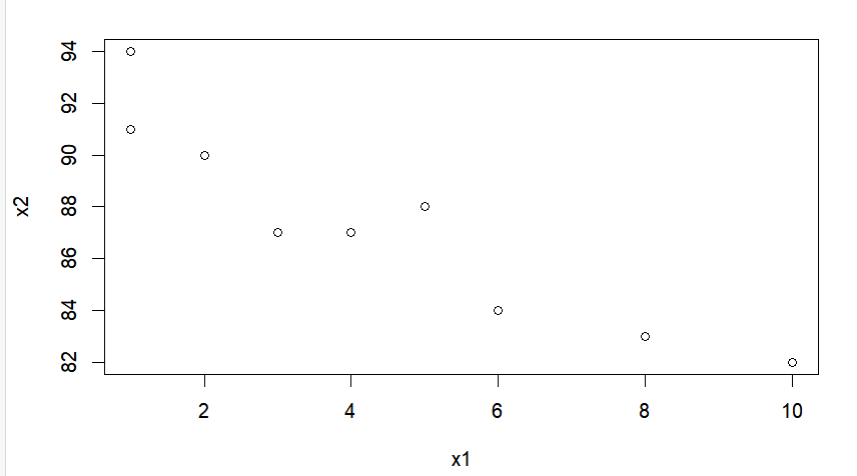
  • 위의 산점도를 보면 x1이 증가할 수록 x2는 떨어지는 것을 확인할 수 있다.

  • R에서는 산점도에 선형선을 표현 할 수 있고 다음과 같이 표현된다.

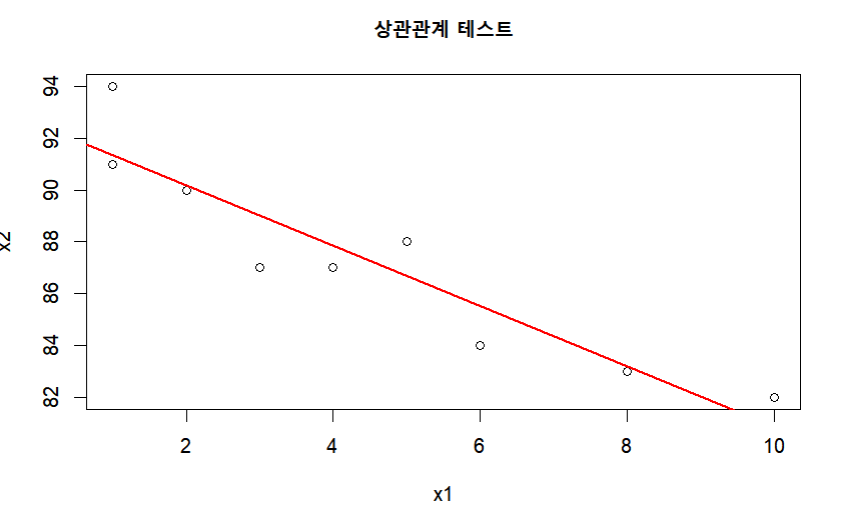
pearson과 spearman의 상관계수

  • Pearson과 Spearman의 상관관계는 -1~1 범위의 값을 가진다. Pearson은 상관계수가 +1이 되도록 하기 위해 한 변수가 증가하면 다른 변수도 일정한 크기만큼 증가해서 완전한 선형을 이룬다.
Pearson 상관계수 Spearman 상관계수
두 변수간에 선형관계 크기를 측정한다. 두 변수간에 선형과 비선형 관계를 모두 측정할 수 있다.
비선형 상관관계를 측정할 수 없고 연속적 변수만 가능하다. 연속적인 변수와 이산형, 순서형도 가능하다.

회귀분석

  • 회귀분석은 변수간의 인과관계를 분석하는 것으로 상관관계에서 두 가지 변수는 변수 간에 원인과 결과가 없는 균등한 변수이고 회귀분석은 변수 간에 원인과 결과가 있는 변수이다.

  • 상관분석은 변수가 1대 1의 관계이지만, 회귀분석은 1대 N의 관계ㅓ에서 데이터를 분석하는 방법이다.

  • 독립변수

    • 독립변수의 변화가 종속변수에 영향을 주는 변수

  • 종속변수

    • 독립변수에 영향을 받는 변수

  • 선형회귀모델과 비선형회귀 모델의 차이

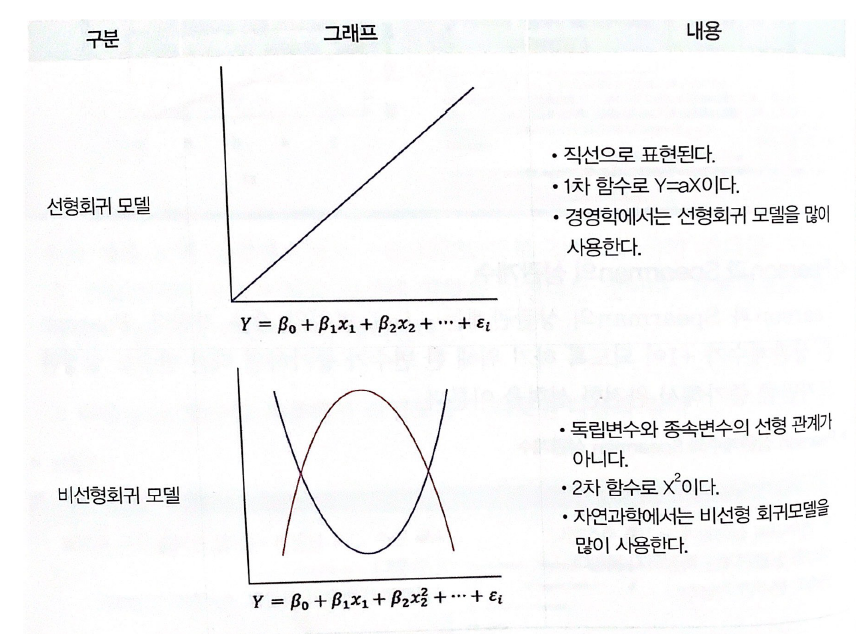
    • 선형회귀모델은 경제학부분에서 비선형회귀는 자연과학에서 많이 사용된다.

선형회귀 모델

  • X변수에 대한 Y변수를 알기 위해서 가장 좋은 직선을 찾기 위해서 분석하는 것이다. 좋은 직선이라는 것은 거리 값이 최소화 되는 선이다.

  • X값에 대한 Y값의 최소값을 알기 위해서 최소제곱법에 의해 직선을 찾게 된다.

  • X변수 한 개로 Y변수를 표현
    Y=β0+β1X+ϵY = \beta_0 + \beta_1X + \epsilon
    ϵ\epsilon은 확률오차를 말한다.(설명할 수 없는 부분)

상관계수와 회귀계수의 차이

  • 상관계수
    • 데이터가 모여있는지 분석하는 것
  • 회귀계수
    • X가 변화할 때 Y가 얼마나 변화하는지를 분석하는 것

비용함수

  • 데이터 분포의 차이를 계산하여 차이가 가장 적은 것을 모델에 사용한다.
    cost=1m∑i=1m(H(x(i))−Y(i))2cost = \displaystyle\frac{1}{m}\sum_{i=1}^{m}(H(x^{(i)})-Y^{(i)})^2

  • 선형회귀 모델을 일차원 방정식으로 표현하면 Y=β0+β1XY = \beta_0+\beta_1X이다.
    이 X값과 Y값은 정해져 있고 β0\beta_0인 절편과 β1\beta_1인 기울기를 예측하여 실제 Y값과 예측한 직선 간의 차이를 최소화하도록 조정해야 하며 이 때, β0\beta_0과 β1\beta_1을 파라미터라고 한다.

  • 경사하강법은 손실을 줄이는 알고리즘으로 미분값(기울기)이 최소가 되는 점을 찾아 Weight(가중치)를 찾는 방법이다.

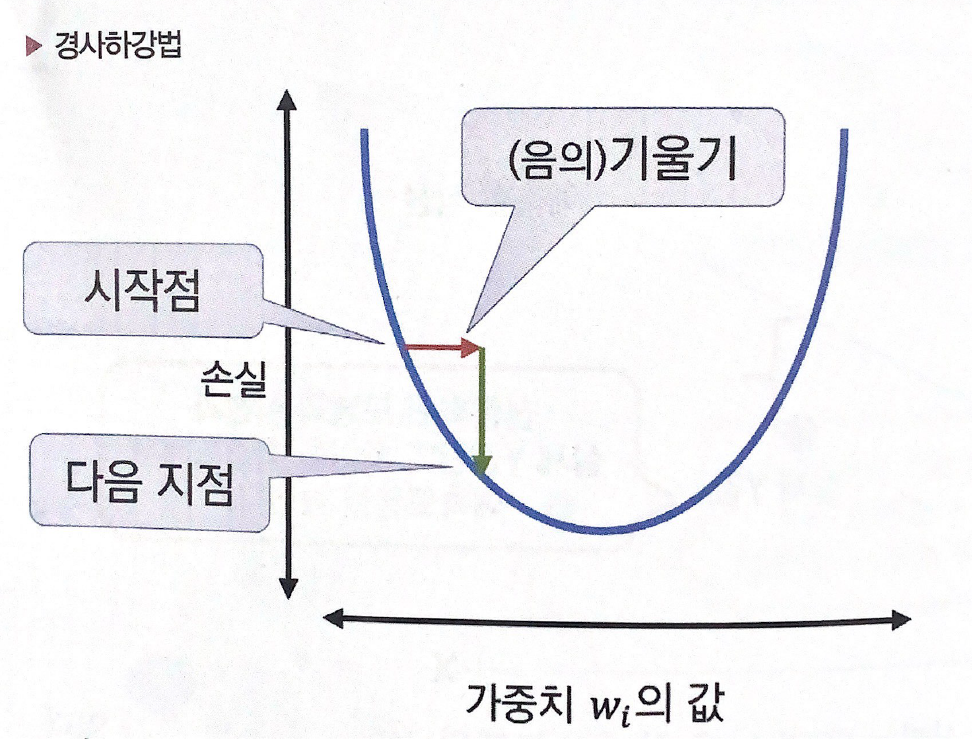
편차, 잔차, 오차의 차이점

  • 편차
    • 평균으로부터 자료가 어떻게 분포되었는지를 확인한다.
    • 분산, 표준편차를 사용한다.
    • (xi−xˉx_i - \bar x), 편차 = 개체 값 - 평균
  • 잔차
    • 회귀분석에서 사용되고 회귀직선 모델에 적합도를 확인한다.
    • ei=(yi−yˉi)e_i=(y_i-\bar y_i)
  • 오차
    • 데이터마이닝에서 모형의 성능을 평가한다
    • 실제 값과 차이를 의미하고 정합도라고 한다.
    • ei=(yi−yˉi)e_i=(y_i-\bar y_i)

다중선형회귀(Multiple Linear Regression)

  • 다중선형회귀는 여러 개의 변수를 두고 종속변수에 미치는 영향을 분석한다.
  • 또한 여러 개의 변수 중에서 종속변수에 가장 영향을 많이 미치는 변수가 무엇인지 분석한다.

변수 선택 방법

  • Enter(입력)
    • 모든 독립변수를 한꺼번에 투입해서 분석한다.
  • Forward(전진)
    • 아무런 변수도 투입하지 않은 상태에서 투입기준에 따라서 하나씩 변수를 입력한다.
  • Backward(후진)
    • 모든 변수를 투입한 후에 제거기준으로 하나씩 변수를 제거한다.
  • Stepwise(단계선택)
    • Forward와 Backward를 하면서 변수를 추가, 제거한다.

다중공선성 문제

  • 다중공선성 문제는 회귀분석에서 독립변수들 간에 강한 상관관계가 나타난는 문제이다.
  • 다중 회귀모델에서 독립변수가 많이 투입되면 회귀식의 설명력이 높아지지만 회귀계수를 신뢰하지 못하게 되는 문제이다. 즉, 다중공선성 문제를 발생시키는 독립변수는 삭제한다.
다중공선성 문제확인
  • 결정계수 R2R_2값이 회귀식의 설명력이 높지만 독립변수의 P-Value 값이 크기 때문에 개별 변수들이 ㄷ유의하지 않는 경우 다중공선성 문제를 분석한다.
  • 독립변수들 간의 상관계수를 구해서 다중공선성 문제를 분석한다.
  • 분산팽창요인을 구해서 10을 넘으면 일반적으로 다중공선성 문제로 의심한다.
다중공선성 문제해결 방법
  • 상관관계가 높은 독립변수 제거
  • 새로운 관측지를 사용 또는 변수를 변형한다.
  • 독립변수 간의 상간관계 이유를 분석하여 해결
  • 주성분분석을 사용해서 예측변수의 수를 상관되지 않는 작은 변수의 집합으로 줄인다.

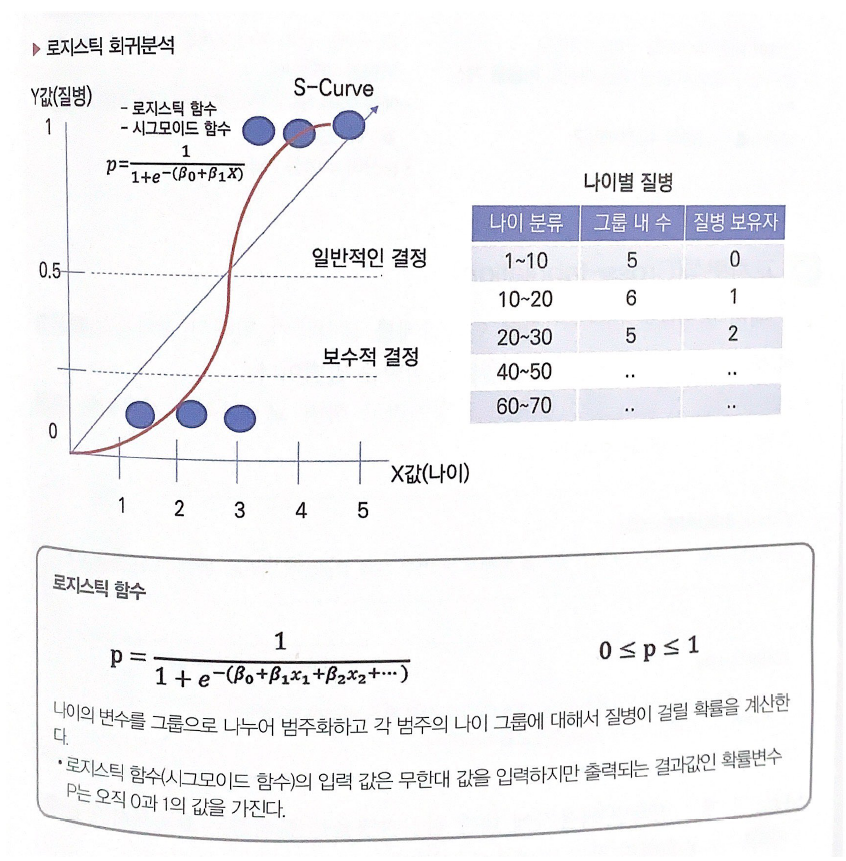
로지스틱 회귀분석

  • 로지스틱 회귀분석은 다중선형회귀 분석과 동일하지만 다중선형회귀는 종속변수가 연속형 변수로 측정되고 로지스틱 회귀분석은 종속변수가 두 가지로 측정된다.
  • 로지스틱 회귀분석은 시그모이드 함수를 사용해서 결과값이 0 혹은 1로 출력된다.
  • 종속변수가 두 가지 분류로 되었을 때 영향을 미치는 독립변수를 분석한다.
  • 독립변수와 종속변수 간의 관계 분석을 인과관계분석이라고 한다.
  • 종속변수는 범주형 변수, 독리변수는 범주형과 연속형으로 혼합된 경우에 사용하는 회귀분석 방법이다.
  • 로지스틱 회귀분석은 결과 값이 1에 속하는 확률을 계산하는 것으로 실제 Y를 0혹은 1의 값을 가지는 확률로 변환한다.

0 혹은 1의 확률 추정

  • P=PP = P (Y=1)일 경우
  • 1−P=P1-P = P (Y=0)일 경우

교차분석

  • 두 개의 질적변수(범주형) 간에 연관관계를 분석하기 위해서 교차분석표(분할표)를 작성하고 변수들 간에 관계를 분석하는 방법이다.
  • 교차분석 X2X^2검정이라고 하며 교차분석에 사용되는 검정 통계량이 X2X^2-분포를 따른다.

사례를 통한 교차분석 이해하기

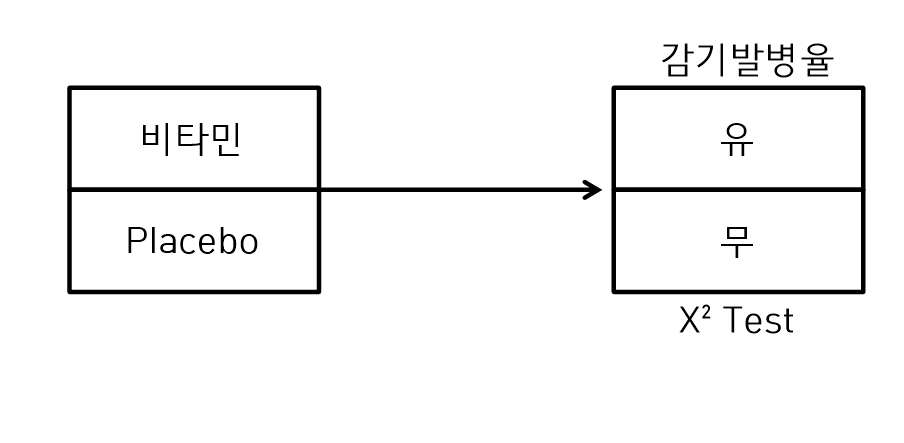
  • 위와 같은 질적변수 2개를 교차분석을 하기 위해서 비타민을 복용한 사람과 복용하지 않는 사람으로 구분한다.

  • 교차분석을 위해 먼저 귀무가설을 정의한다

    • 비타민 복용과 감기발병은 관계가 없다
setwd("C:\\Users\\km253\\OneDrive\\바탕 화면\\Rlanguae")
data <- read.csv("vitamin.csv", fileEncoding = "euc-kr")
attach(data)
dim(data)
str(data)

  • 교차분석을 위해 데이터 프레임을 만든다.
x<- data$비타민복용
y<- data$감기발생
class(x)
result <- data.frame(Level = x, Pass=y)
table(result)

  • table함수를 통해 각 변수의 누개를 알 수 있다.

  • 교차분석표를 사용하기 위해서 gmodels를 설치하고 교차분석표를 생성한다.

table(result)
install.packages("gmodels")
library(gmodels)
CrossTable(x,y)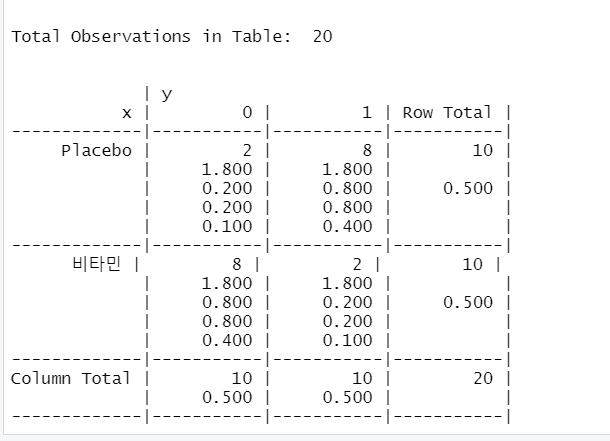

  • 교차분석을 진행한다.
chisq.test(x,y)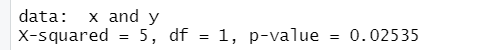

  • p-value가 0.05보다 작으므로 귀무가설은 기각된다.

교차분석의 종류

  • 사전 교차분석
    • 실험을 설계하고 특정한 실험을 하면서 분석을 수행한다.
    • 비타민과 감기 발병률 등이 있다.
  • 사후 교차분석
    • 이미 발생한 사건을 기준으로 분석해야 하는 것을 의미한다.
    • 미세먼지와 사망률에 대한 분석이 있다.
profile
이강민
NullpointException
이전 포스트

ADsP - 가설

다음 포스트

ADsP - 데이터마이닝 개요

0개의 댓글