지도학습, 예측, 분류
지도학습
- 데이터마이닝의 지도학습은 목표변수가 있는 경우 사용하는 방법으로 예측과 분류기법으로 나누어진다.
예측기법과 분류기법의 종류
- 예측기법
- 회귀분석, 선형모형, 비선형 모형
- 분류기법
- 의사결정나무, 서포트 벡터 머신, 판별분석, 로지스틱 회귀분석
예측과 분류
- 예측
- 기존 데이터 및 미래의 상황에 대한 가정을 활용해서 분석하는 것으로 고객의 구매활동 등을 예측한다.
- 분류
- 다수의 객체를 그룹화하는 것으로 학습데이터를 사용해서 오분류율을 최소화하는 분류규칙을 생성하는 것이다.
분류
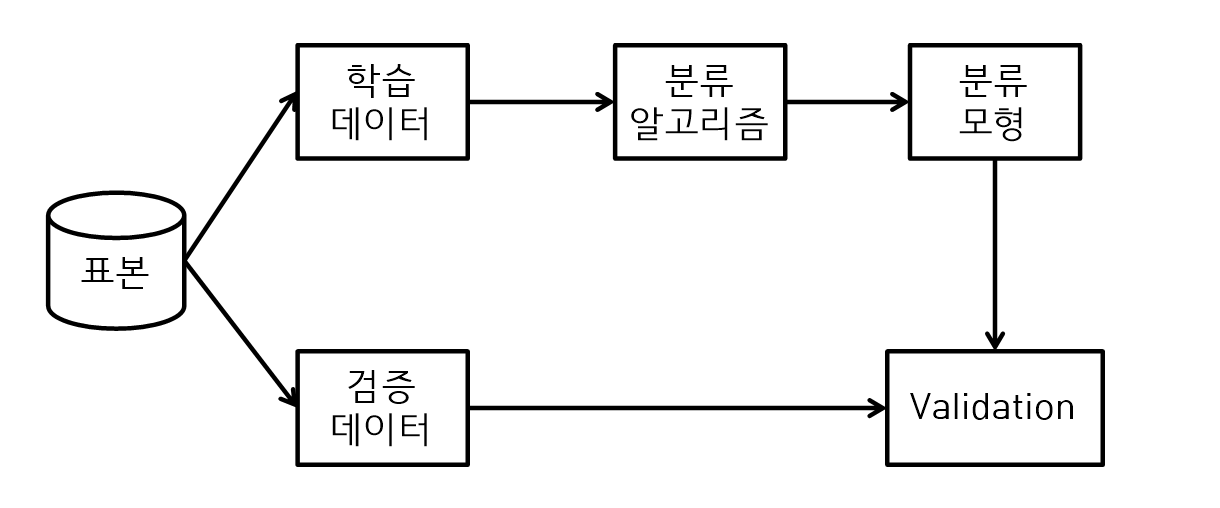
- 분류는 표본으로부터 학습 데이터와 검증 데이터를 랜덤 샘플링을 통해 샘플링한다.
- 학습 데이터는 분류 알고리즘(예 : 의사결정나무)을 사용해서 분류모형을 만들고 검증 데이터로 분류모형의 타당성을 확인(validation)한다.
- 분류모형은 새로운 실제 데이터가 입력 되었을 때 오분류율을 최소화할 수 있도록 한다.
과적합
- 예측모형에서 테스트 데이터에 대해서 과한 적합모형을 선택하면 실제 데이터를 적용한경우에 더 높은 오차가 발생한다.
학습 데이터와 검증데이터
- Train data
- 분석모델을 만들기 위해서 사용되는 학습용 데이터
- Validation data
- 분석모델을 검증하기 위한 데이터
- Test data
- 최종 분석모델을 확인하기 위한 결과용 데이터
다중 회귀분석
다중 회귀분석 방법
- k개의 독립변수 ~가 종속변수 Y를 종속하는 경우 다중 회귀분석을 사용한다.
- 즉, 하나의 종속변수에 다수의 독립변수가 존재할 경우 사용한다.
다중회귀분석 공식
,
~
- 회귀계수 는 다른 독립변수가 일정한 경우 의 변화량이다.
다중 회귀분석 변수 선택 방법
- 변수선택은 전진 선택법, 후진 제거법, 단계별 방법이 있다. 단계별 방법은 전진선택법에 의해서 변수를 추가한다. 변수가 추가되고 중요도가 유의수준에 포함되지 않으면 추가한 변수가 제거된다.
- 전진 선택법
- 독립변수 중에서 종속변수에 영향이 가장 큰 변수부터 모형에 포함시키는 방법
- 후진 제거법
- 독립변수를 모두 포함시켜서 모형을 만들고 가장 영향이 적은 변수부터 제거하는 방법
- 단계별 방법
- 전진 선택법에 의해서 변수를 추가한다. 변수가 추가되고 중요도가 유의 수준에 포함되지 않으면 추가한 변수가 제거된다.
다중공선성
- 다중회귀분석에서 독립변수들 사이에 상관관계가 발생하는 현상
만약 다중공선성이 발생하면 회귀계수에 대한 해석이 불가능해진다.
K-인접기법
K-인접기법
- K-인접기법은 Instance-based Learning이다.
- KNN은 분류 및 예측 방법 중에서 Instance-based Learning으로 모델을 생성하지 않고 데이터를 분류하거나 예측할 때 사용하는 방법이며 학습 데이터의 패턴을 분석하여 데이터를 분류하고 예측한다.
- K에서 가장 가까운 이웃들을 사용해 분류하는 방법이고 비선형 모델이다.
- KNN은 범주형 데이터를 분류할 수도 있고 연속형 데이터로 예측할 수가 있다.
K-인접기법의 특징
- Instance-based Learning
- 각각의 인스턴스(관측지)를 사용해서 새로운 데이터를 예측할 수가 있다.
- Memory-based Learning
- 모든 학습 데이터를 메모리에 저장하고 예측한다.
- Lazy Learning
- 모델을 만들지 않고 테스트 데이터로 작동하는 알고리즘이다.
K-인접기법과 유클리드 거리 값 계산
- 새로운 데이터는 가장 가까운 군집에 분류된다.
- 이때 가장 가까운 거리를 계산할때 유클리드 거리 공식을 많이 사용한다.
K-인접기법 장단점
- 장점
- 간단하며 쉽게 이해 가능
- 효율적인 방법
- 표본 수가 많을 때 좋은 분류방법
- 단점
- 최적 K를 선택하기 어렵고
- 데이터가 많으면 분석속도가 느리다.
- 표본의 수가 많아야 정확도가 높다.
R을 이용한 K-인접기법
#패키지 설치
install.packages("class")
install.packages("gmodels")
install.packages("scales")
# 연결
library(class)
library(gmodels)
library(scales)
attach(iris)
set.seed(1000)
# 세팅
N = nrow(iris)
tr.idx = sample(1:N, size=N*2/3, replace=FALSE)
iris.train <- iris[tr.idx, -5]
iris.test <- iris[-tr.idx, -5]
trainLabels <- iris[tr.idx,5]
testLabels <- iris[-tr.idx,5]
train <- iris[tr.idx,]
test <- iris[-tr.idx,]
#분석
md <- knn(train = iris.train, test = iris.test, cl=trainLabels, k=5)
md
#검증
CrossTable(x=testLabels, y =md, prop.chisq = FALSE)
의사결정나무
의사결정나무
- 의사결정나무는 의사결정 규칙(Decision rule)을 도표화하고 분류 및 예측을 할 수 있는 데이터마이닝기법이다.
- 기계학습 기법 중 하나로 나무 형태로 분석하는 방법으로 분석 과정을 직관적으로 이해하기 쉽기 때문에 설명력이 좋은 장점이 있다.
분류나무와 회귀나무의 구분
| 구분 | 분류나무 | 회귀나무 |
|---|---|---|
| 특징 | 목표변수가 범주형 변수이다. 분류를 지닌다. |
목표변수가 수치형 변수이다. 예측을 한다. |
| 사용가능한 재귀분할 의사결정 알고리즘 |
CART(지니지수 사용) C4.5(엔트로피 사용),C5.0 CHAID(카이제곱 통계량) |
CART |
- 분류나무의 불순도 측정은 CART, C4.5, C5.0, CHAID이고 회귀나무의 불순도 측정은 CART이다.
의사결정나무의 장단점과 활용
의사결정나무 장점
- if~then으로 규칙 생성이 가능하고 이해하기가 쉽다.
- 데이터베이스 SQL을 사용해서 표현이 가능하다.
- 설명령이 좋기 때문에 많이 사용된다.
의사결정나무 단점
- 연속형 변수 값을 예측할 때는 적당하지 않다.
- 시계열 분석이 어렵다.
의사결정나무 활용분야
- 통신회사에서 이탈고객을 분류
- 신규 신용카드 발급대상을 분류
- 은행에서 대출가능한 고객을 분류
의사결정나무 모형 분석절차
① 의사결정나무 형성
- 분석 목적을 정의하고 분석목적에 따라서 분리기준과 정지규칙을 지정해서 의사결정나무를 형성한다.
② 가지치기
- 부적절한 규칙을 가지고 있는 가지를 제거한다.
- 부적절한 추론규칙을 가지고 있는 가지를 제거한다.
- 검증용 데이터를 사용해서 모형의 예측을 검토한다.
③ 최적 Tree 분류
- 의사결정나무의 타당성을 평가한다.
- 검증용 데이터를 사용해서 교차 타당성을 평가한다.
④ 해석 및 예측
- 의사결정나무를 해석하고 예측모형을 설정한다.
의사결정규칙
- 의사결정나무는 의사결정규칙에 의해서 가지치기를 하면서 수행된다.
분리기준
- 목표변수의 분포를 가장 잘 구별해주는 기준, 종속변수의 분포를 잘 구분하는 가에 대한 지표
분리
- 이지분리
- 양쪽 2개로만 분리
- CART를 사용한다.
- 다지분리
- 여러 개로 분리할 수가 있다.
- C4.5, CHAID를 사용한다.
불순도 알고리즘
- 얼마나 다양한 범주의 객체가 포함되어 있는지를 수치로 표현한 것
- 불순도 알고리즘을 사용해서 그룹으로 분할하는 기준이 된다.
- 불순도 알고리즘으로 지니지수와 엔트로피 지수, 정보이익, 카이제곱 통계량 등이 있다.
정지규칙
- 불순도가 떨어지지 않는 경우 분리를 중단한다.
- 자식노드에 남은 샘플의 수가 너무 적은 경우에 중단한다.
가지치기
- 의사결정나무의 깊이가 깊어지면 과적합이 발생할 수 있다.
- 따라서 불필요한 마디를 제거한다.
오분류율(Miss Classfication rate)
- 관측지가 속하는 실제 집단과 다른 집단으로 잘못 분류한 비율을 의미한다.
- 분류모형의 성과를 판단하는 기준이다.
재위적 분할 의사결정나무 알고리즘
CART(Classfication And Regression Trees)
-
CART는 C4.5와 매우 유사한 방법으로 수치적 분할기준으로 사용해서 트리를 형성한다.
-
목표변수가 범주형인 경우에 지니지수를 사용하고 연속형인 경우 분산을 사용해 이진분리를 한다.
-
의사결정나무로 분류나무와 회귀나무에 모두 사용가능
-
개별 입력변수 및 입력변수들의 선형결합들 중 최적분리를 찾을 수가 있다.
-
평가지수로 지니 불순도를 사용한다. 지니 지수란 불확실성을 의미하고 0에 가까울 수록 좋은 것이다. 즉, 0이라는 것은 100% 모두 맞춘것이다.
-
학습데이터로 의사결정나무를 성장시키고 검증용 데이터를 이용하여 가지치기를 한다.
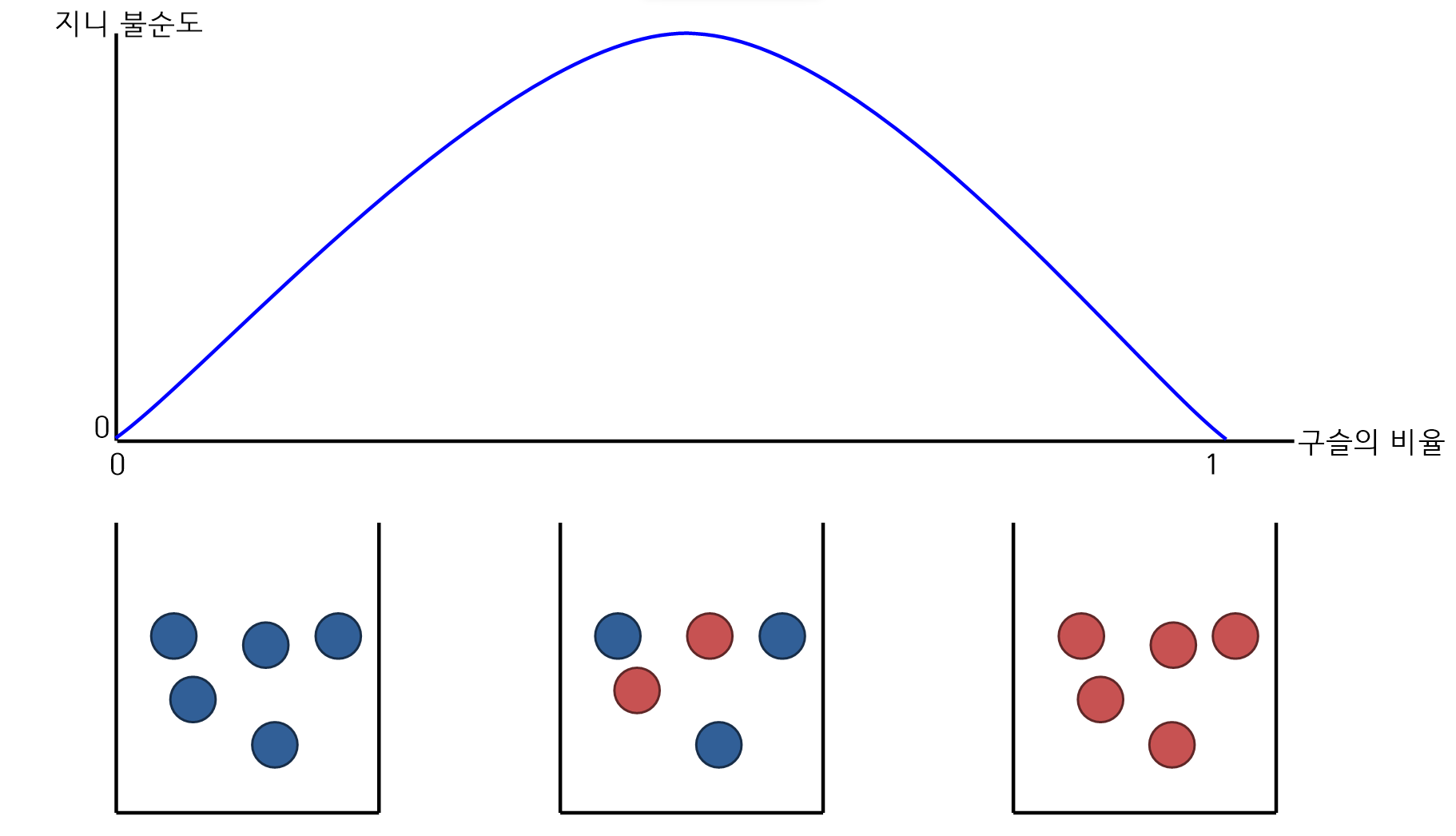
-
지니 불순도는 집합에서는 "순도"를 의미하며 파란구슬, 빨간구술만 있는 있는 것이 순수도가 높은 것이다.
-
지니 불순도는 0이면 순수도가 가장 높은 것이다.
지니불순도
- 는 전체집합에서 집단에 속하는 관측지의 비율이다.
- 는 요소들의 집합으로 위의 예에서는 빨간구슬과 파란구슬만 있으므로 가 된다.
- 만약 전체구슬이 110개가 들어가 있고 37개는 빨간구슬, 73개는 파란구슬일 때 지니 불순도는 다음과 같다.
단계별 지니지수 구하기
- 이지분리로 나누기
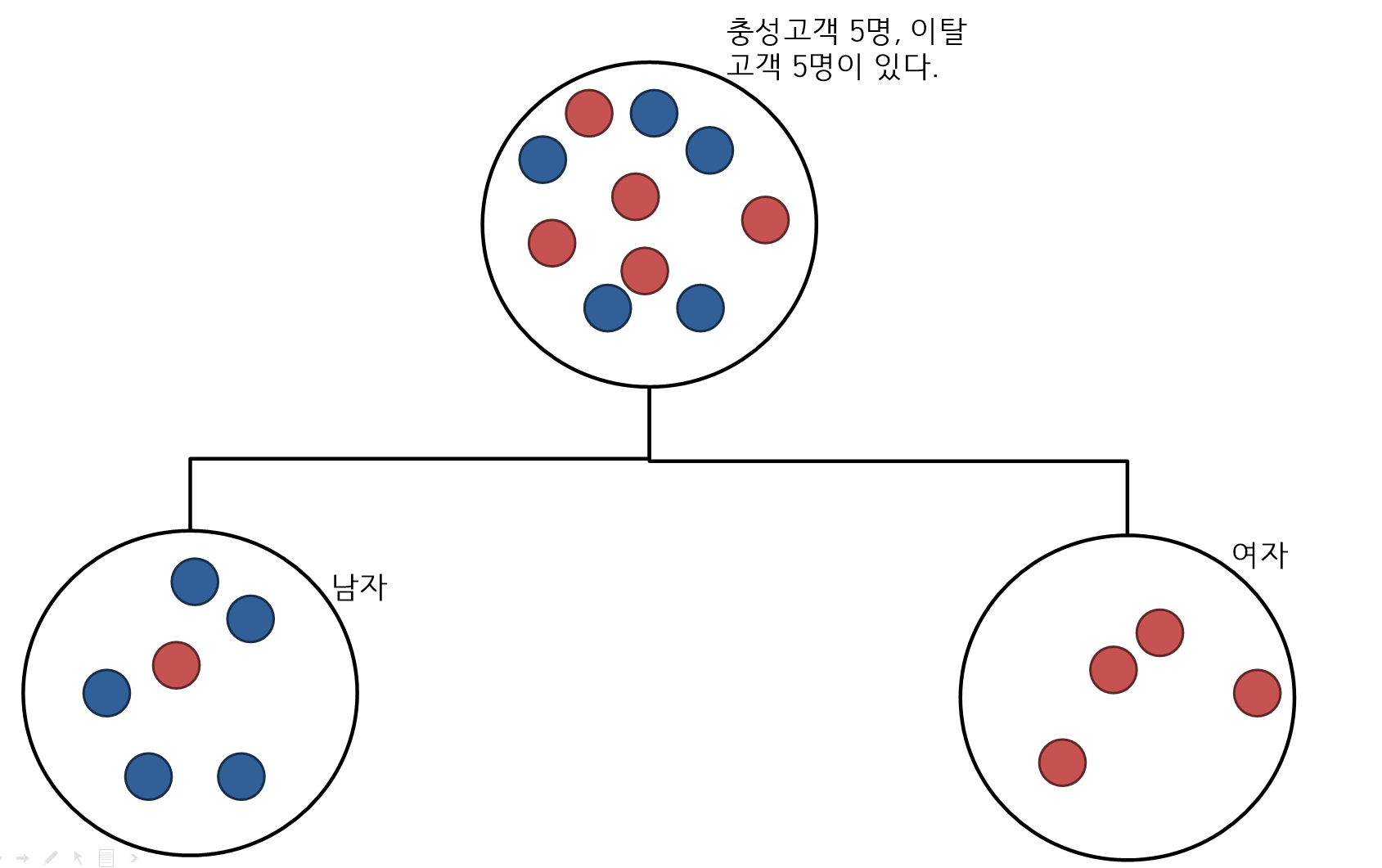
1단계 지니지수
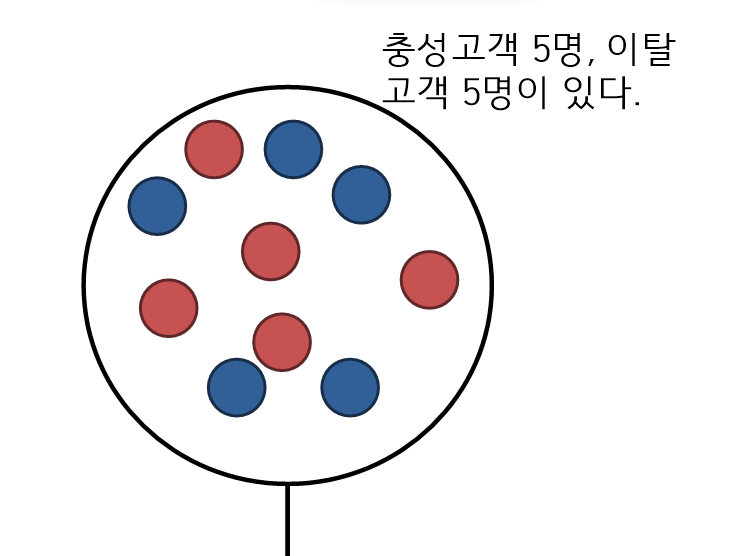
- 1단계 지니지수는 가장 상위의 지니지수로 계산은 다음과 같다.
2단계 지니지수
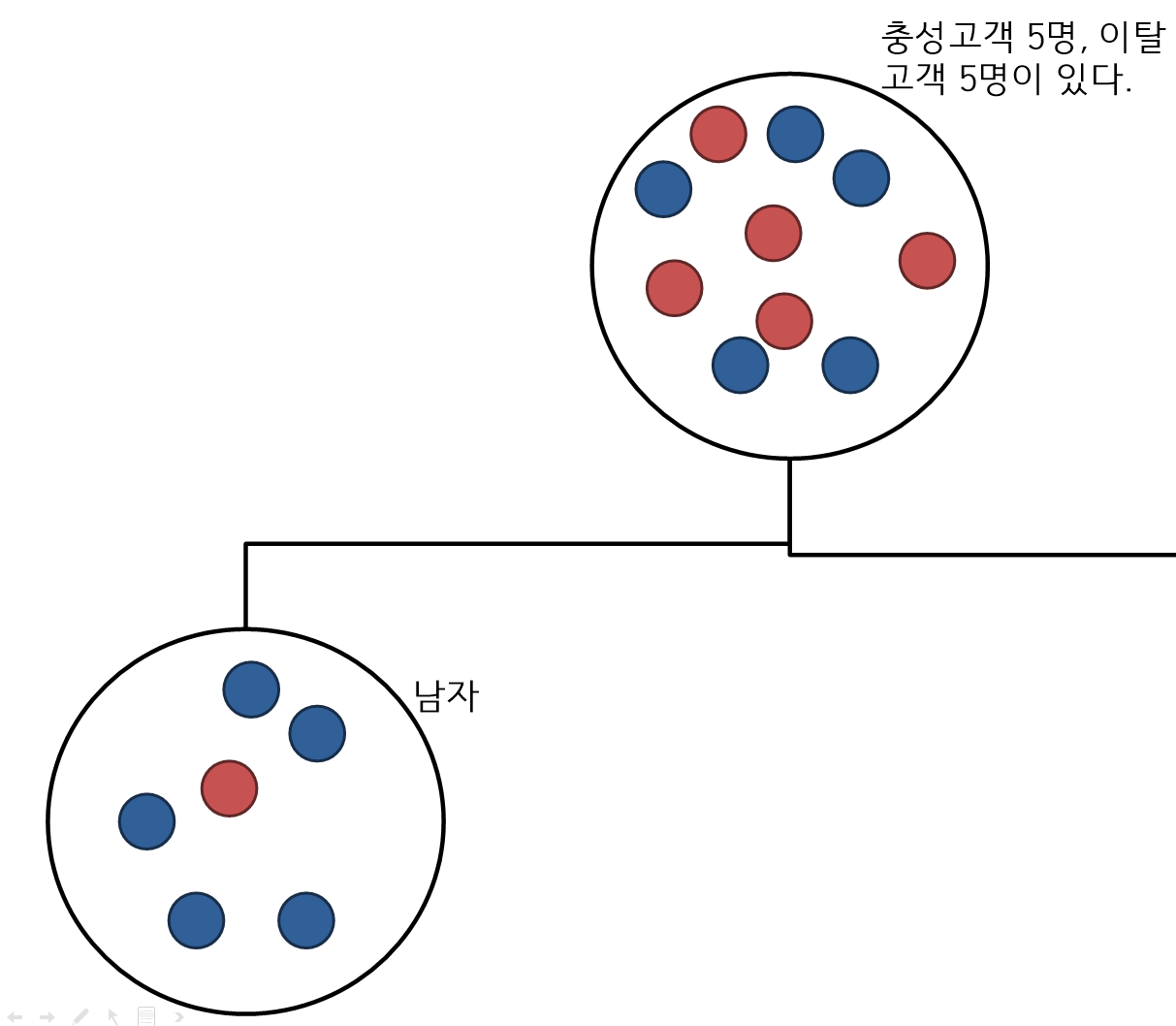
- 한쪽의 트리의 지니지수를 의미하며 남자 중의 이탈과 출성고객의 불순도를 구한다.
- 6개의 구슬이 남자이고 6개 중 5개는 충성, 1개는 이탈고객을 말하며 불순도는 다음과 같다.
3단계 지니지수
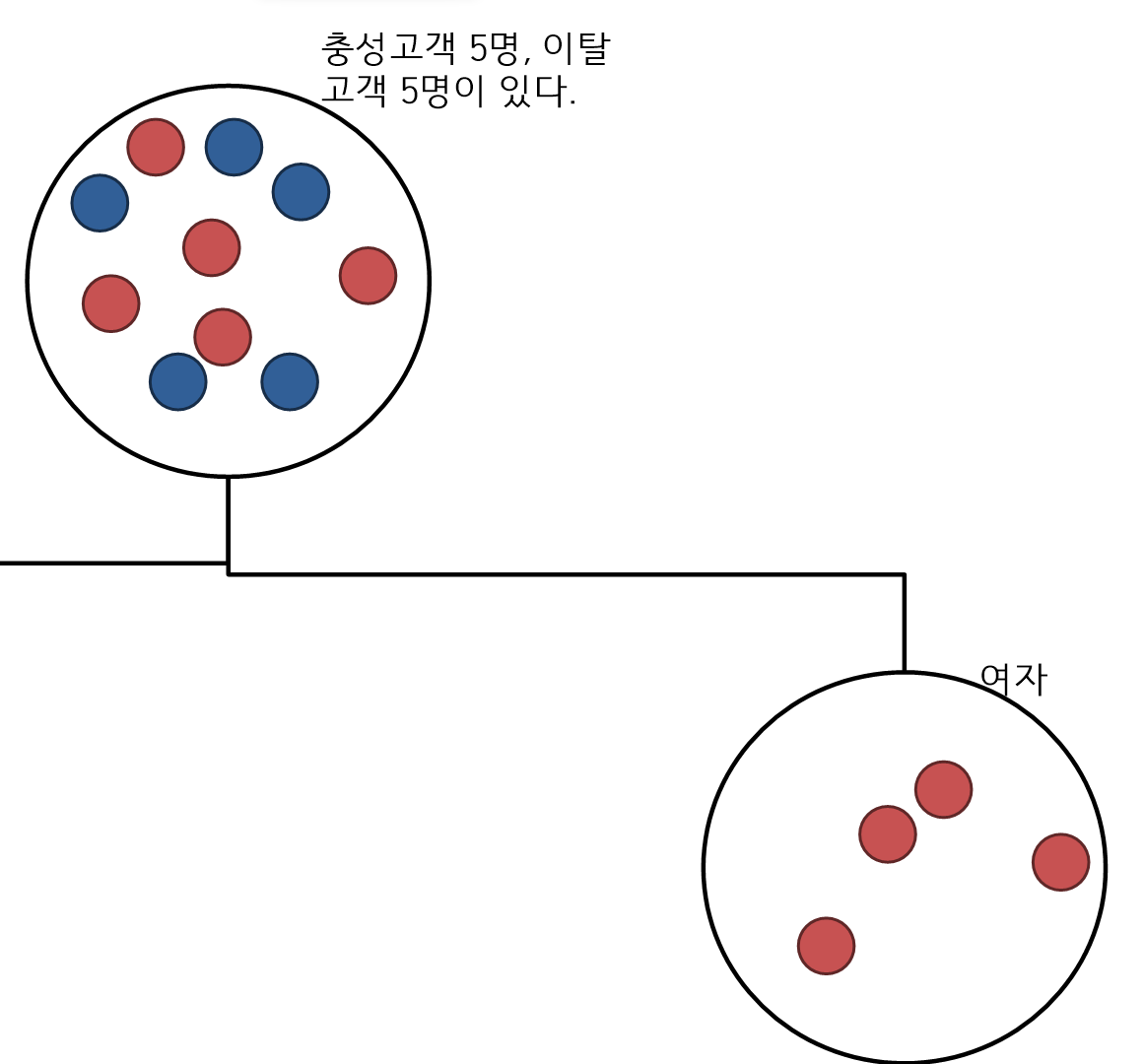
- 나머지 한쪽의 트리의 지니지수를 구한다.
- 4개의 구슬이 여자이며 전부 이탈고객이다.
4단계 최종 지니지수
- 위의 과정을 거쳐 다음과 같이 구할 수 있다.
C4.5
- C4.5 알고리즘은 93년 퀼른에 의해서 제안된 알고리즘이다.
- 다지분리가 가능하고 범주형 입력변수의 범주 수만큼 분리가 가능하다.
- 분류나무 및 회귀나무 분석이 가능하다.
- 불순도를 측정하기 위해서 엔트로피 지수를 사용한다.
CHAID(CHI-squared Automatic Interaction Detection)
- CHAID의 불순도 알고리즘은 Chi-square 통계량, F통계량을 이용한다.
- 명목형, 순서형, 연속형 등 모든 종류의 목표변수와 분류변수를 적용할 수 있는 알고리즘으로 이진트리 구조로 모형을 형성하는 방법을 제공한다.
- 가지치기가 없고 분류나무에서만 사용이 가능하다.
재귀적 분할 의사결정 알고리즘 비교
| 구분 | CART | C4.5 | CHAID |
|---|---|---|---|
| 분류나무 | O | O | O |
| 회귀나무 | O | O | X |
| 예측변수 | 범주 및 수치 | 범주 및 수치 | 범주형만 가능 |
| 불순도 알고리즘 | Gini지수 | Entropy | Chi-square 통계량 |
| 분리 | 이지분리 | 다지분리 | 다지분리 |
| 정지규칙 | 모형개발 후 가지치기 | 모형개발 후 가지치기 | 가능 |
| 교차검증 | 학습 데이터로 나무생성, 검증 데이터로 검증 |
학습데이터만 사용 | 없음 |
분류나무
- 목표변수가 번주형 변수로 좋음, 나쁨 혹은 우수 및 불량 등으로 만들어진다.
- 분류나무 알고리즘은 CART, C4.5, CHAID가 있다.
회귀나무
- 목표변수가 연속변수로 총구매액, 매출액 등으로 만들어진다.
- 목표변수의 평균에 기초하여 트리를 형성한다.
- 목표변수가 수치형 변수이다.
R언어를 사용한 의사결정나무
# 의사결정나무 패키지 설치
install.packages("tree")
install.packages("caret")
# 패키지 연결
library(tree)
library(caret)
attach(iris)
#학습데이터와 검증데이터로 분류
set.seed(2000)
# 학습데이터 100, 검증데이터 50 저장
N <- nrow(iris)
tr.idx <- sample(1:N, size= N*2/3, replace=FALSE)
train <- iris[tr.idx,]
test <- iris[-tr.idx]
# iris 데이터를 분리해서 결과를 testdata에 저장한다.
dim(train)
dim(test)
treedata <- tree(Species~., data = train)
treedata
# 의사결정 나무를 표시한다.
plot(treedata)
text(treedata, cex=1)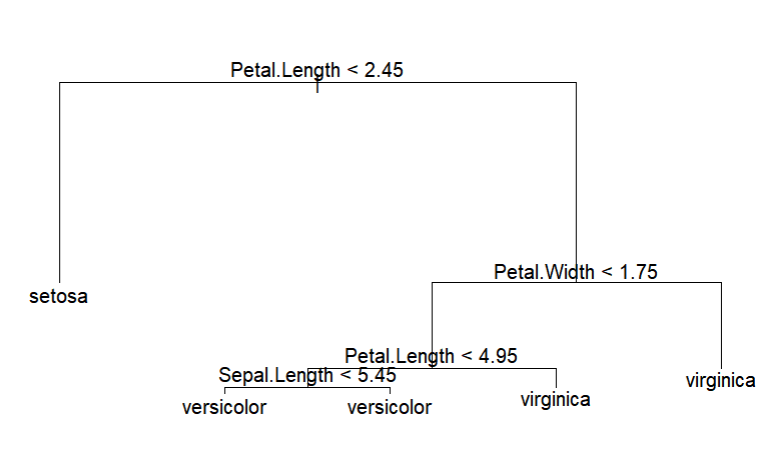
- 표시된 의사결정나무
#최적 k를 구한다.
cv.tr <- cv.tree(treedata, FUN = prune.misclass)
cv.tr
plot(cv.tr)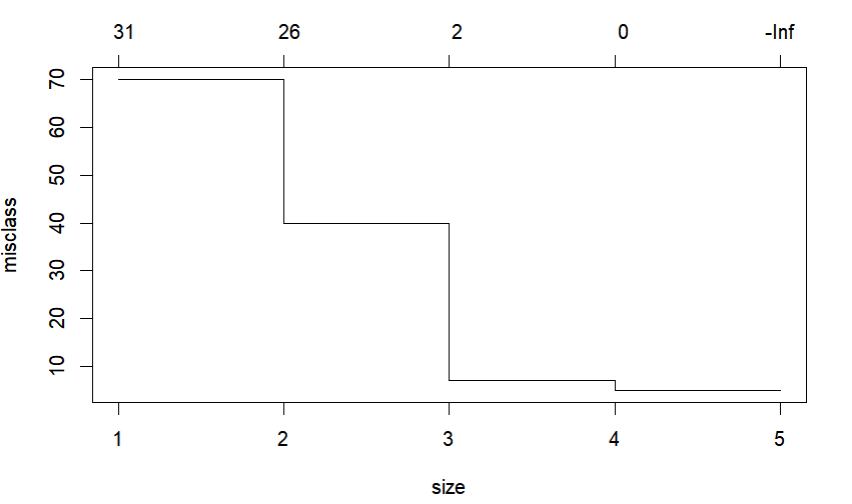
# 최적 의사결정나무, 3으로 결정하여 작성
prune.tr <- prune.misclass(treedata, best=3)
plot(prune.tr)
text(prune.tr, pretty = 0, cex=1)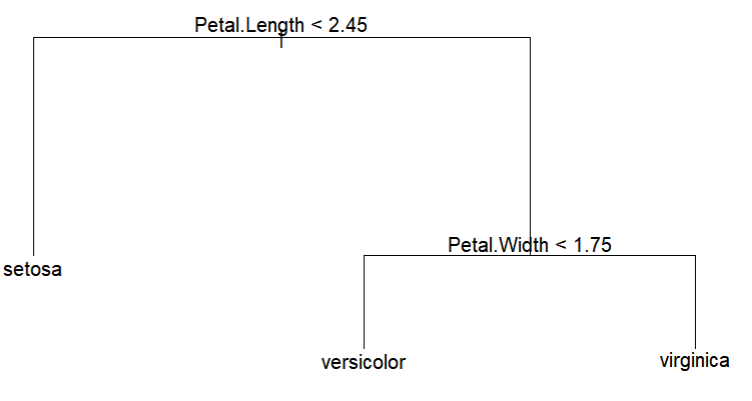
랜덤포레스트
랜덤 포레스트
- 의사결정나무의 과적합 문제를 해결한 알고리즙으로 앙상블기법을 사용한다.
- 랜덤 포레스트는 분석과정에서 다수의 결정트리로부터 분류하거나 평균 예측지를 분석한다.
- 여러 개의 의사결정나무를 만들고 투표를 통해서 다수결로 결과를 결정한다.
- 랜덤 포레스트는 배깅기법 중에 하나이다.
앙상블
- 여러 개의 학습모델을 결합하여 데이터를 분석하는 것이다.
즉, 여러 개의 분류모델을 활용하여 최적의 모델을 선택하거나 여러 개의 변수를 입력하여 어떤 변수가 가장 좋은 변수인지를 확인한다. - 앙상블은 예측력은 우수하나 설명력이 떨어진다.
앙상블 기법
- 투표
- 동일한 훈련 세트를 하난 두고 여러 개의 분류모델을 사용해서 분석
- 배깅
- 하나의 모델을 사용한지만 훈련세트를 여러 개의 샘플로 만들고 알고리즘마다 다른 훈련세트를 사용하는 방법이다.
- 부스팅
- 샘플을 선택할 때 잘못 분류된 데이터 50%를 재학습하거나 가중치를 사용한다.
투표
- 하나의 훈련세트를 사용하고 여러 개의 분류모델을 사용해서 분석하는 방법
- 하나의 훈련세트는 동일 데이터를 각각 모델에게 동일하게 넣어 준다.
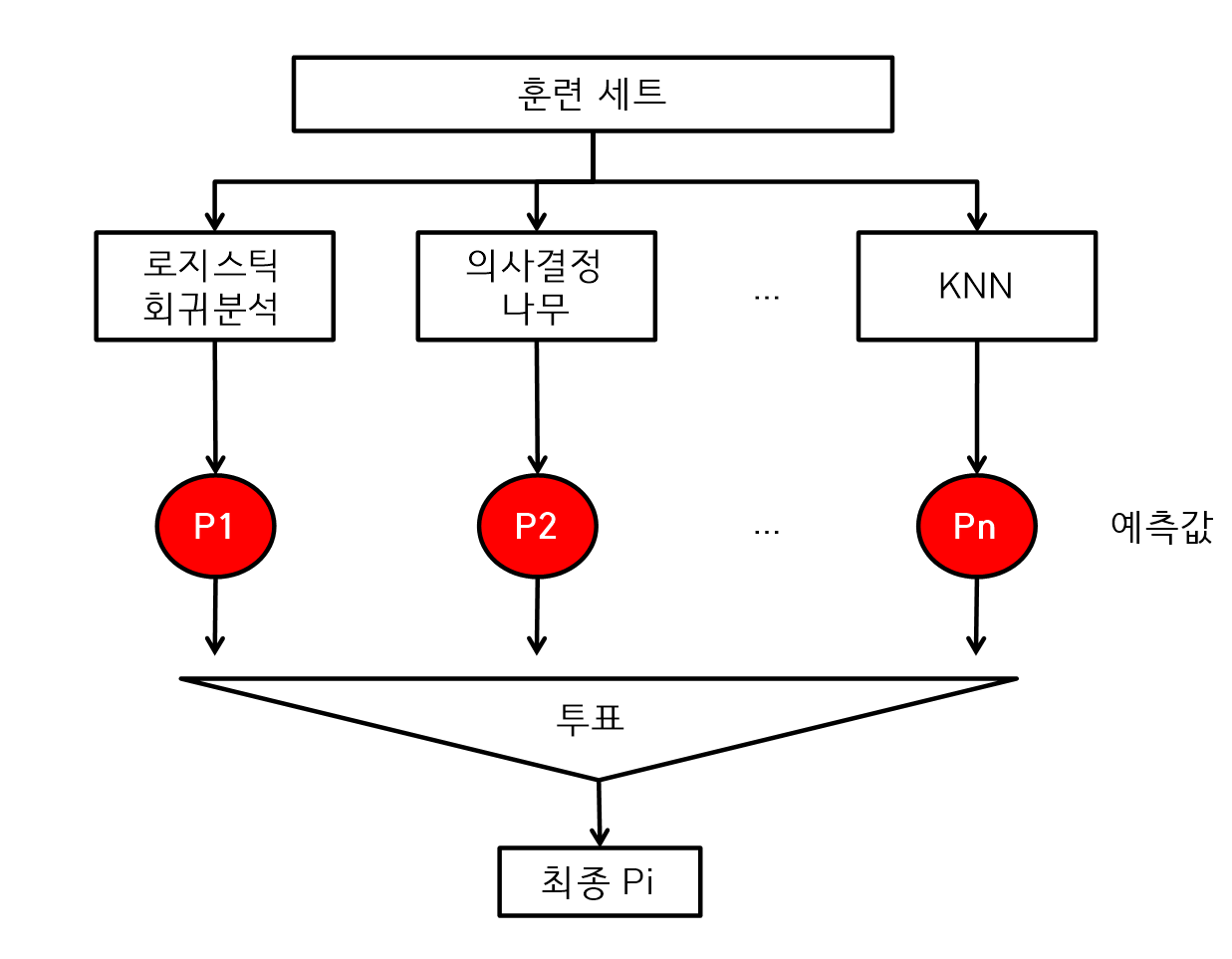
- 투표에서 각각의 분석모델의 예측값이 다르면 가장 많이 나온 결과를 선택한다.
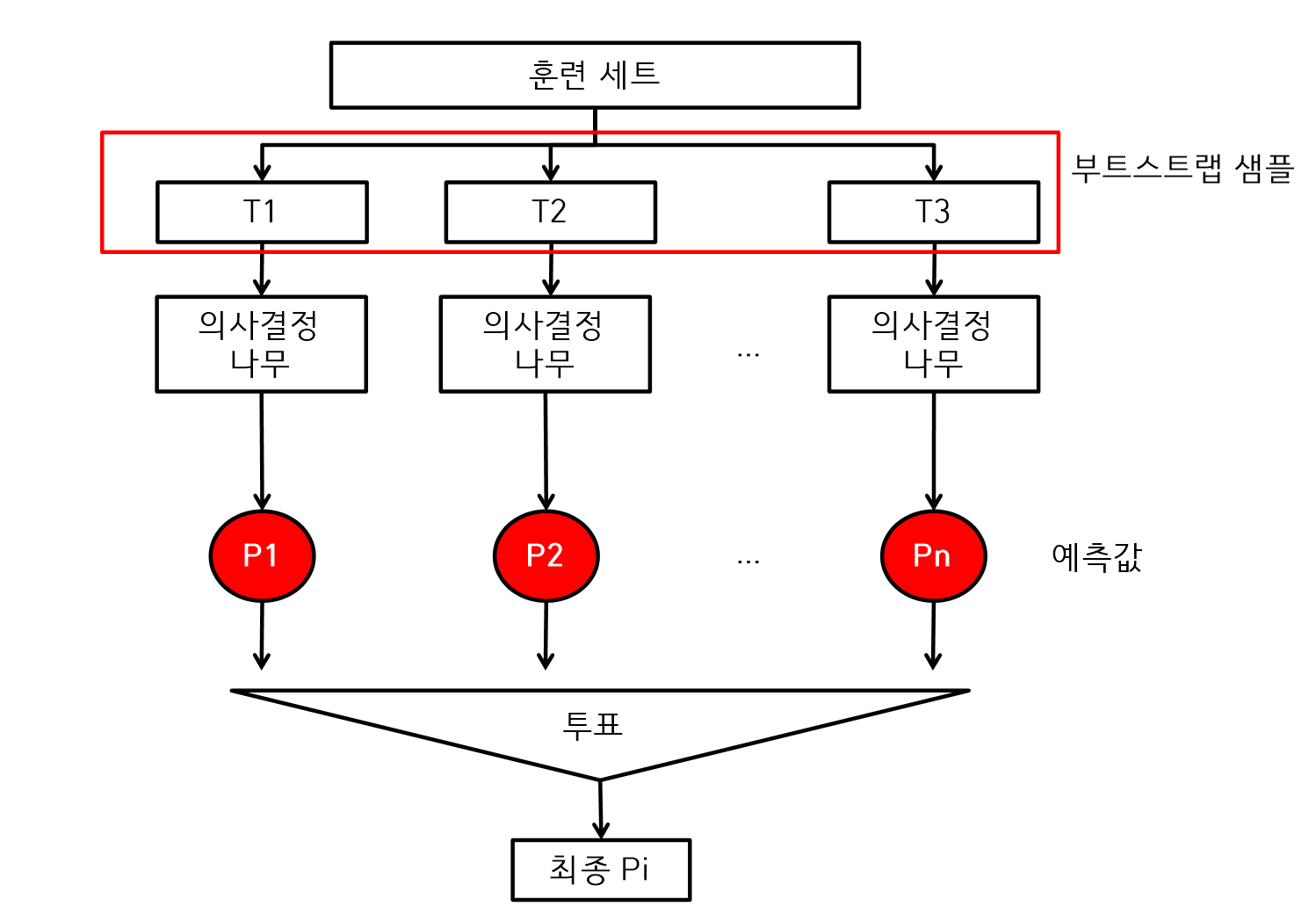
배깅
- 하나의 모델을 사용하지만 훈련세트를 여러 개의 샘플로 만들고 알고리즘마다 다른 훈련세트를 사용하는 방법이다.
- 부트스트랩을 실시하는데 데이터로부터 복원추출한다. 데이터 추출 시에 중복을 허용하기 때문에 훈련세트에서 다양한 데이터가 추출된다.
- 부트스트랩이란?
- 모집단에 대해서 어떤 가정도 하지 않고 표본에서 표본 데이터를 반복적으로 추출한다. 즉, 복원 추출법으로 표본에서 새로운 여러 개의 표본을 만든다.
- 모집단에 대해서 어떤 가정도 하지 않고 표본에서 표본 데이터를 반복적으로 추출한다. 즉, 복원 추출법으로 표본에서 새로운 여러 개의 표본을 만든다.
랜덤 포레스트
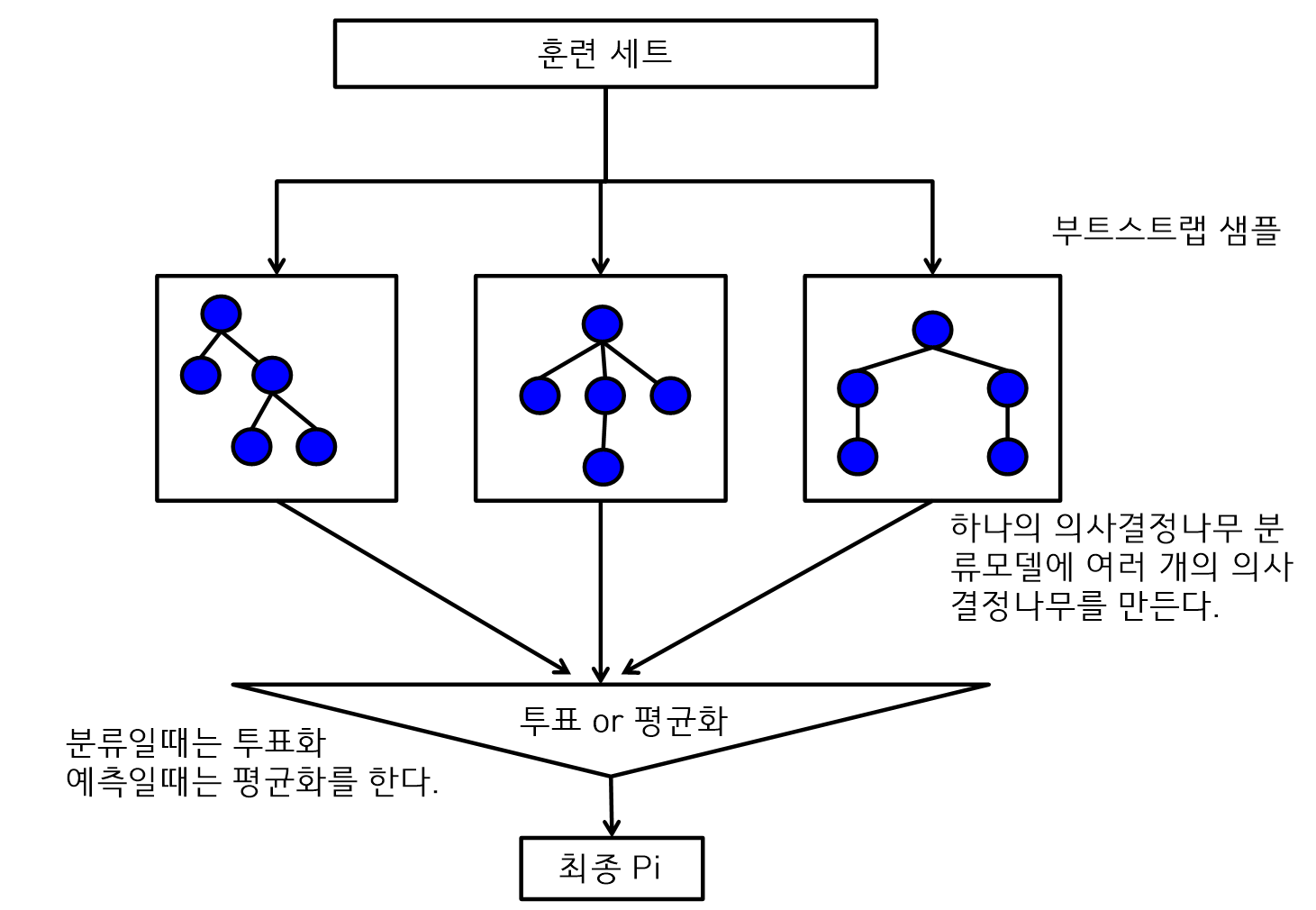
- 배깅 방법 중의 일종으로 단일 분류 알고리즘인 의사결정나무만을 사용한다.
- 부트스트랩 기법을 사용해서 여러 개의 샘플 데이터를 추출하고 모델을 구축
- 최종 결과는 분류일때는 투표방식, 예측 일때는 평균화를 사용한다.
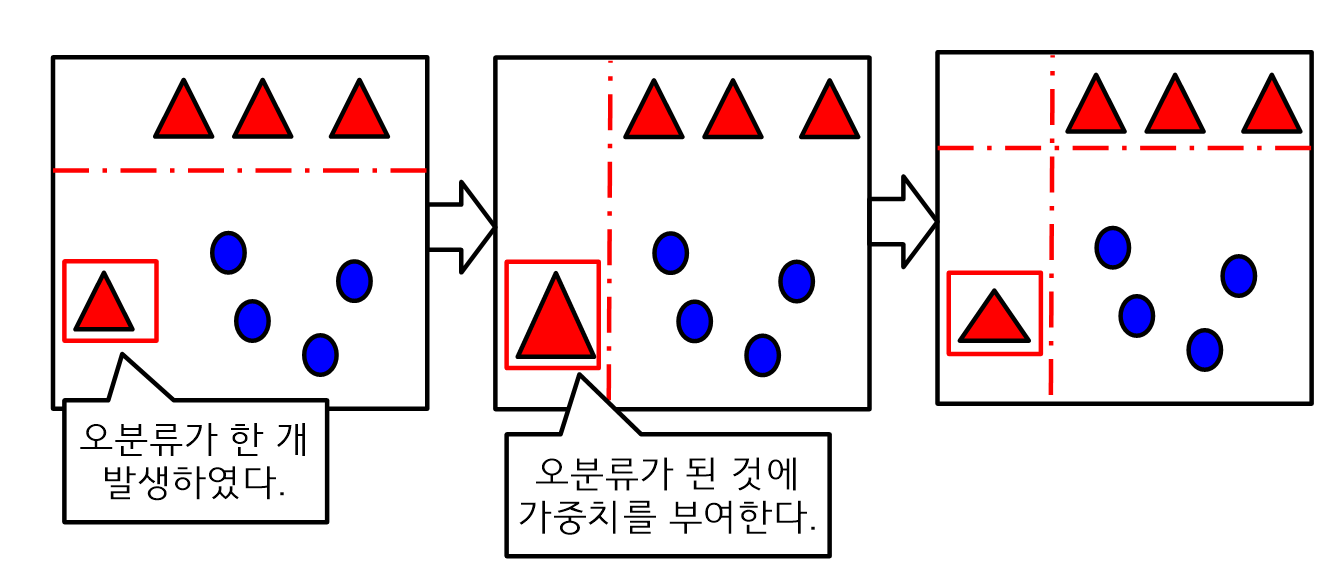
부스팅
- 부스팅은 전체훈련세트를 사용하고 잘못 분류된 데이터에 가중치를 적용한다.
- 샘플을 추출할 때 잘못 분류된 50% 데이터를 재학습한다.
- 부스팅 방법은 실제 적용할 때 가중치를 구현하기가 어렵다.
- AdaBoost 방법
R을 사용한 랜덤 포레스트
# 랜덤포레스트 패키지 설치
install.packages("randomForest")
# 패키지 연결
library(randomForest)
attach(iris)
#학습데이터와 검증데이터로 분류
set.seed(2000)
# 학습데이터 100, 검증데이터 50 저장
N <- nrow(iris)
tr.idx <- sample(1:N, size= N*2/3, replace=FALSE)
iris.train <- iris[tr.idx, -5]
iris.test <- iris[-tr.idx, -5]
trainLabels <- iris[tr.idx, 5]
testLabels <- iris[-tr.idx,5]
train <- iris[tr.idx,]
test <- iris[-tr.idx,]
rf <- randomForest(Species~., data = train, importance=T, mtry=4)
rf
randomForest::importance(rf)
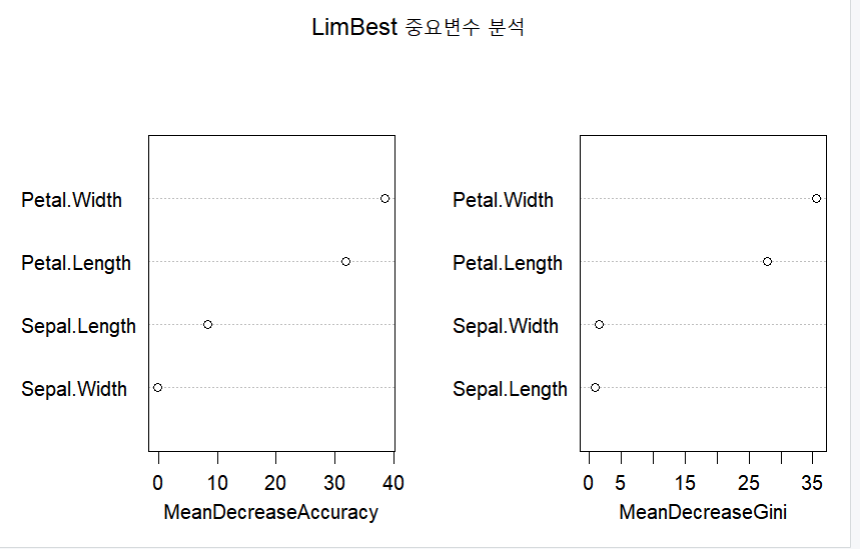
varImpPlot(rf, main="LimBest 중요변수 분석")
- 아래의 랜덤포레스트 결과에서 중요 변수를 확인한다.
서포트 벡터 머신
서포트 벡터 머신
- 고차원 혹은 무한차원의 공간에서 초평면을 찾아서 이를 이용하여 분류 및 회귀분석을 수행한다.
- 지도학습으로 모든 속성을 사용한 전역적 분류 모형이다.
- 속성들 간의 의존성을 고려하지 않는 모델이다.
- 서포트 벡터 머신은 데이터를 분류할 수 있는 선을 찾고 선형회귀 분석은 데이터를 정확하게 맞출 수 있는 선을 찾는다.
- 서포트 벡터 머신과 회귀분석의 차이점은 회귀분석은 데이터를 잘 분류하면 분석을 종료하지만, 서포트 벡터머신은 최적의 분류 직선을 찾는다.
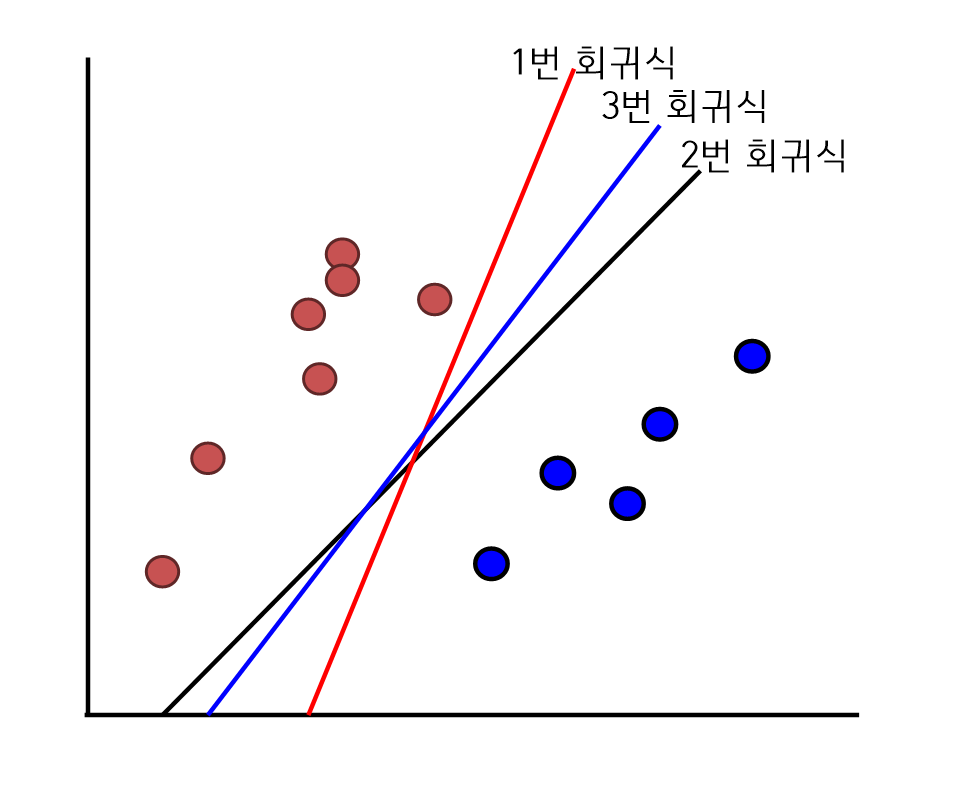
서포트 벡터 머신의 장단점
- 장점
- 모델의 정확도가 우수하다.
- 범주형 및 연속형 데이터를 모두 처리한다.
- 단점
- 데이터가 많으면 속도가 떨어진다.
- 모델에 대한 해석이 어렵다.
선형 SVM(Linear Support Vector Machine)
- 선형 SVM은 객체를 분류할 때 초평면을 기준으로 객체 간에 마진을 최대화 되도록 분류하는 모델이다.
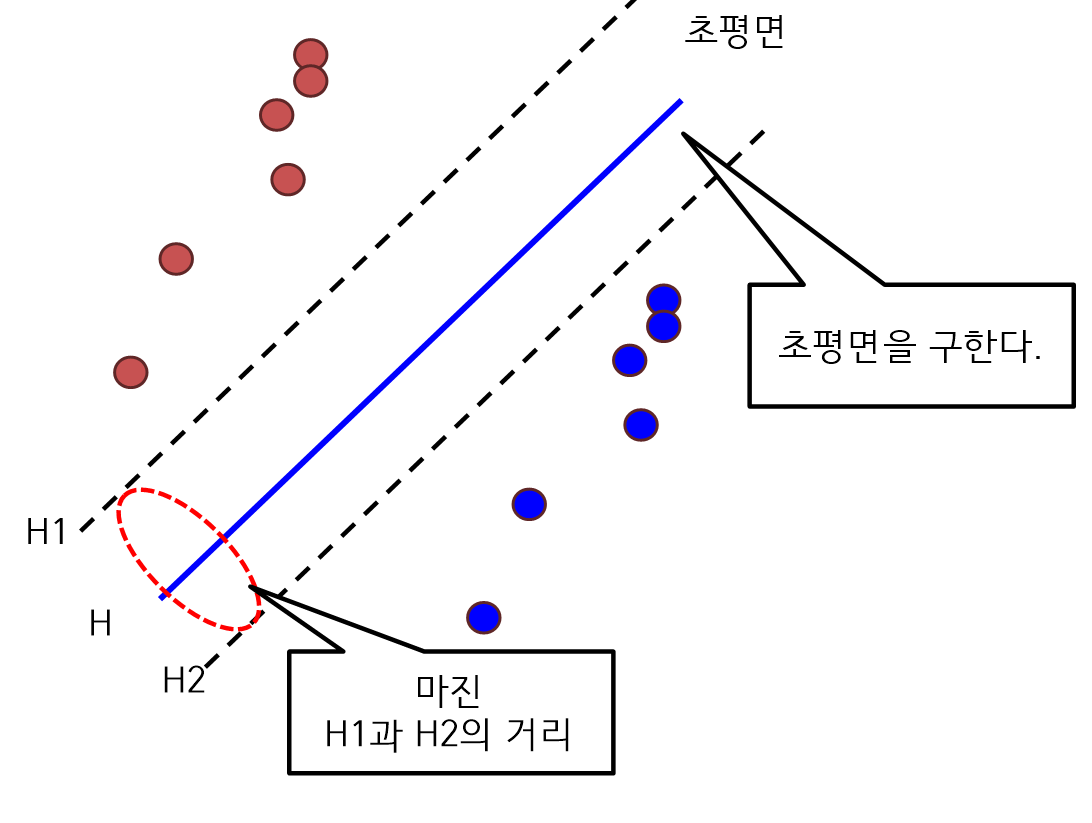
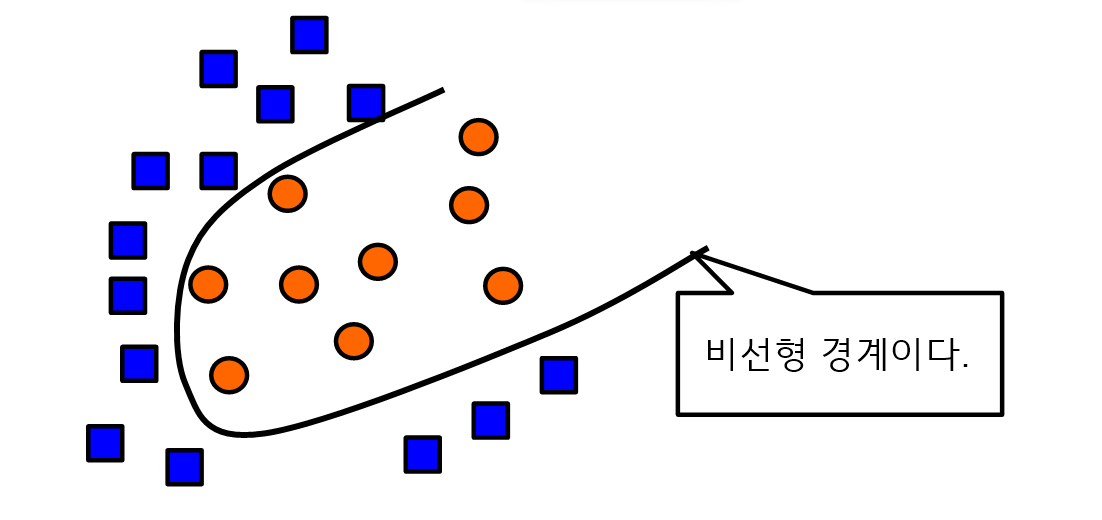
비선형 SVM(Non-linear Support Vector Machine)
- 비선형패턴은 선형 패턴의 Feature space로 변환해서 분류하는 모델이다.
- Kernel method는 선형 패턴의 Feature space로 변환한다. 즉, 비선형 경계면을 도출한다.
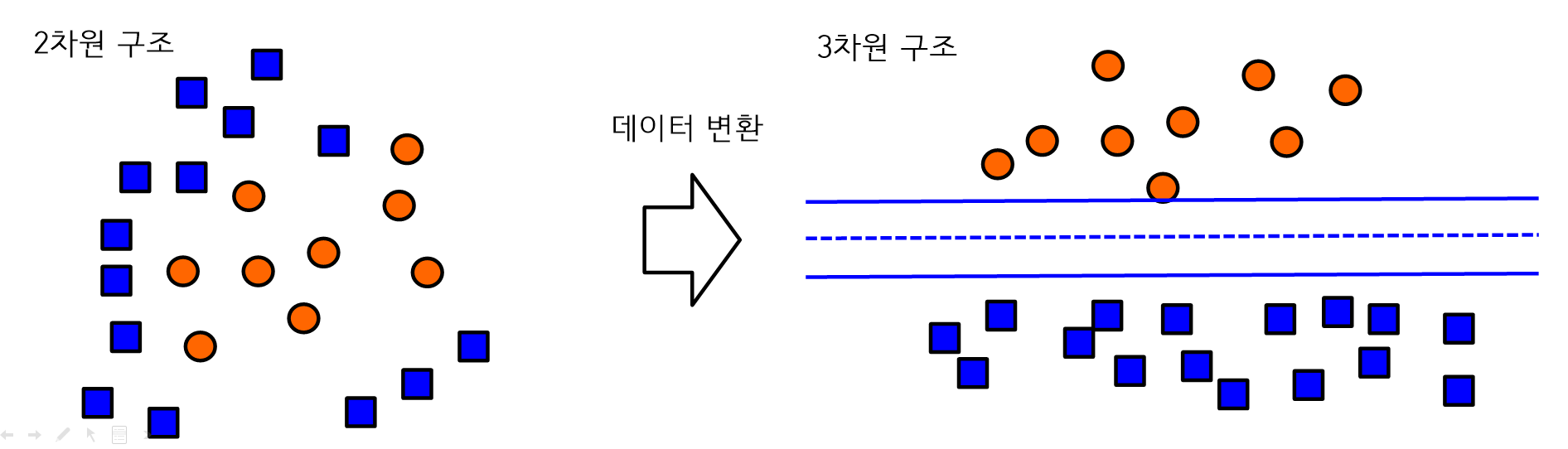
Kernel method
- Kernel method란, 비선형 경계면을 찾는 방법을 제공한다.
- 비선형 패턴을 분리하기 위해서 비선형 패턴의 입력공간을 선형패턴의 Feature space로 변환한다.
- 비선형 데이터 변환
Soft margin
- Soft margin은 초평면이 존재하지 않는 비선형 구조에서 해를 구하는 것이다.
나이브 베이즈 분류모형
조건부 확률
- A조건이 추가되는 경우 다른 사건 B가 발생하는 확률이다.
확률의 계산
- S : 표본공간 = 전체개수
- A : 사건 또는 사상 = 관심이 있는 부분
교사건(A and B)
- 교사건
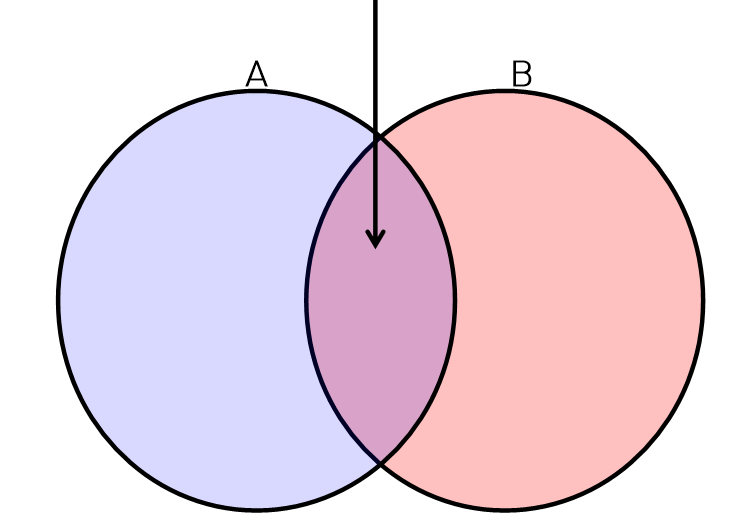
조건부 확률
, 단
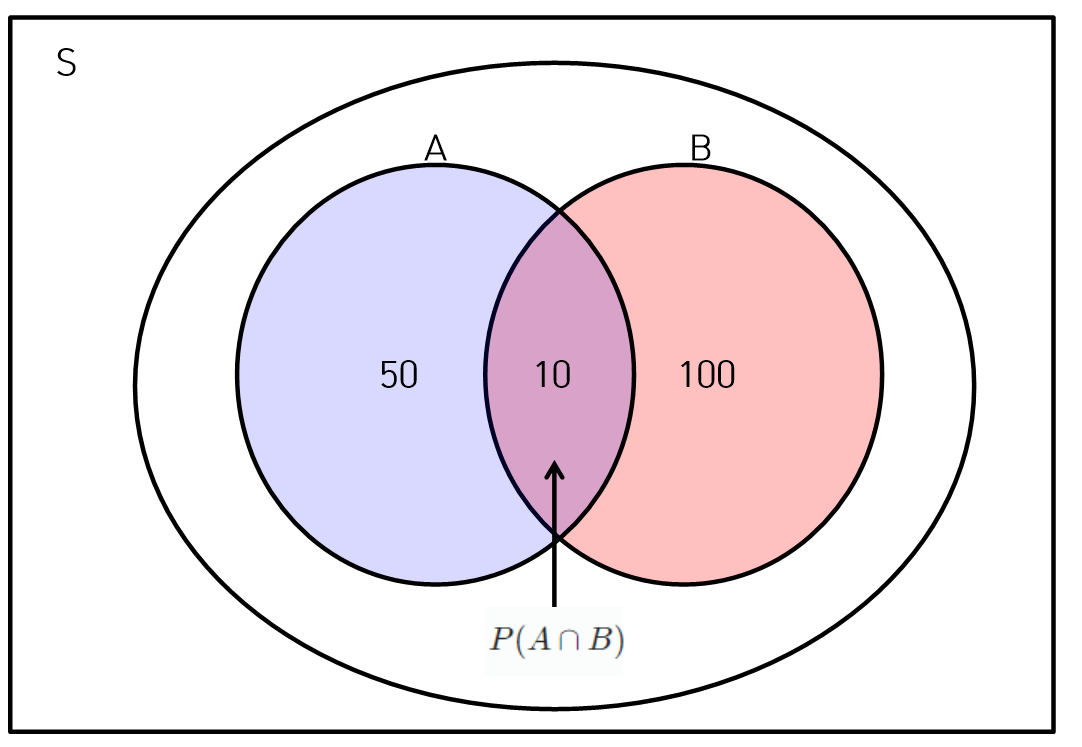
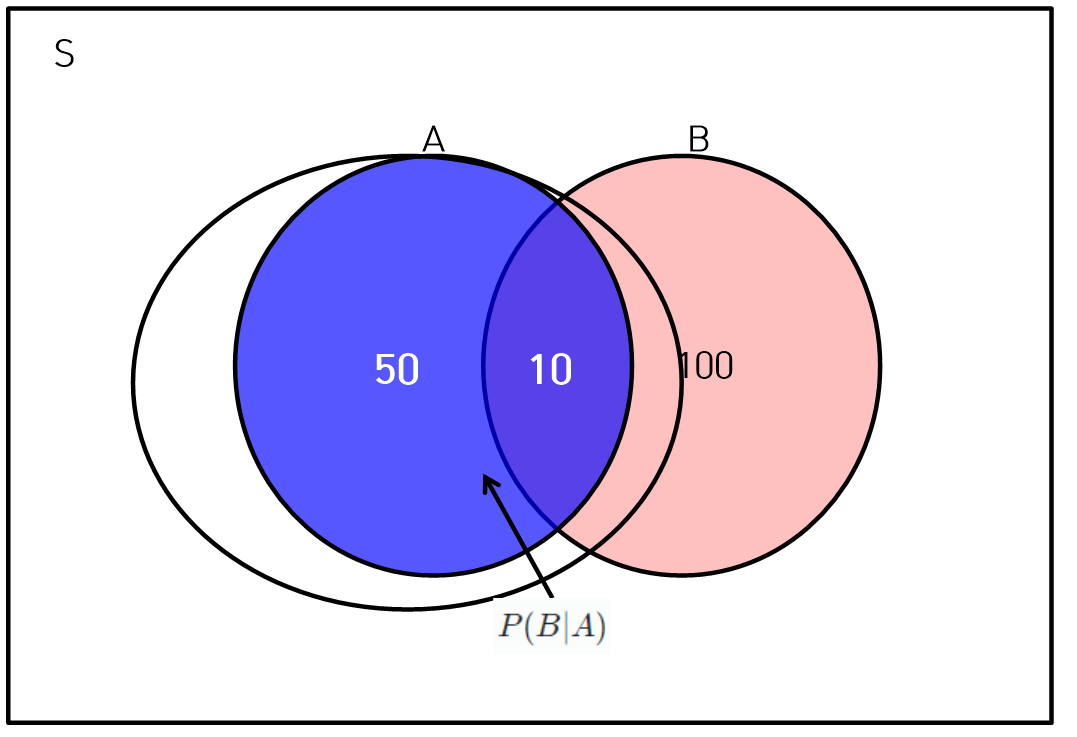
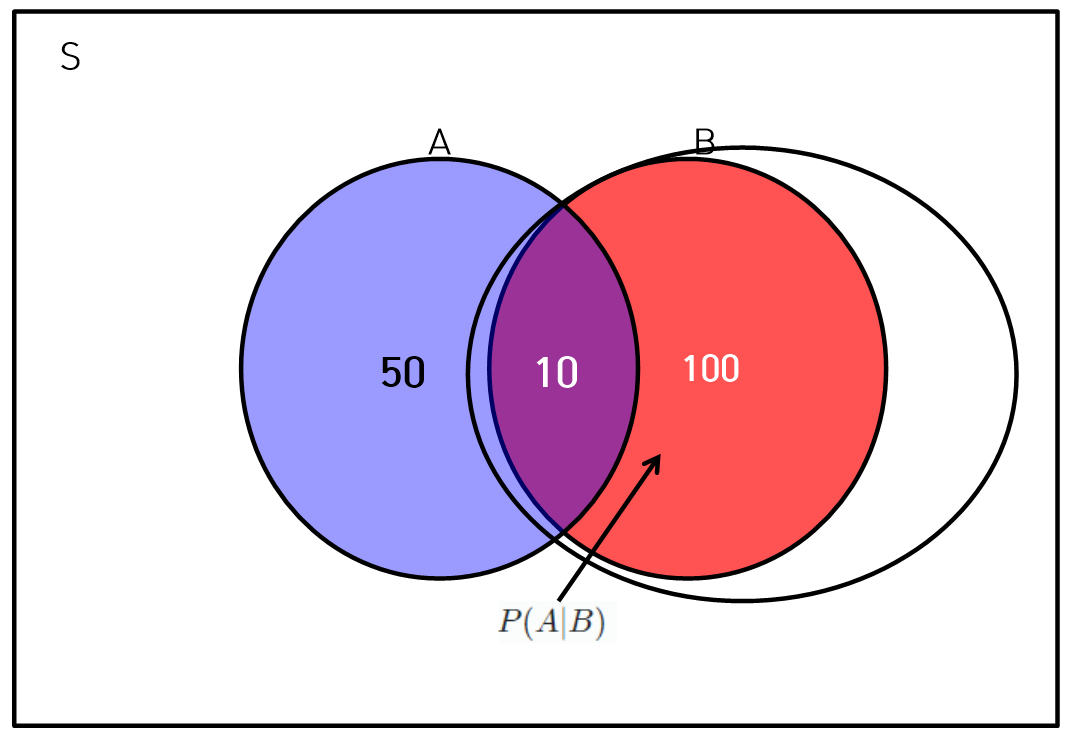
- 독립하는 A, B변수의 는 와 같다. 마찬가지로 는 와 같다.
A와 B가 독립하는 경우 규칙
- 조건부 확률에서 배반사건이라는 것은 A와 B가 교집합이 없느 경우를 의미한다.
나이브 베이즈 분류
- 나이브 베이즈 분류모형은 데이터를 분류할 때 데이터 셋의 모든 특징들이 독립적이고 동등하다고 가정하고 데이터를 불류한다.
- 자료에 대한 가정을 하지 않고 대용량 데이터 자료에서 동작이 가능하다.
- 스팸필터 및 키워드 검색을 활용한 문서분류에 사용한다.
- 베이즈 정리를 적용하여 데이터를 구성하고 각 변수는 독립적으로 가정해서 입력벡터를 분류하는 확률 모형이다.
- 범주형 예측자료만 가능하다.
- 베이즈 정리를 적용하여 데이터를 구성하고 변수는 독립적으로 가정해서 입력벡터를 분류하는 확률모형이다.
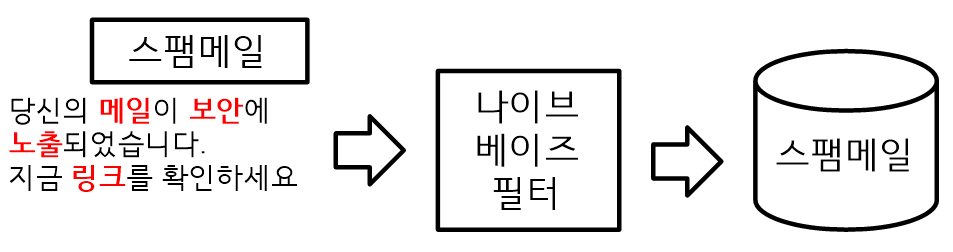
- 위의 예에서 메일, 보안, 노출, 링크 등의 단어가 등록되어 있다면 스팸 필터는 각 단어를 서로 무관하게 판단한다. 즉, 메일이 나타날 확률은 보안, 노출과 무관하게 판단한다.
- 스팸으로 등록된 단어가 많으면 스팸일 확률이 높아지기 때문에 스팸으로 분류한다.
나이브 베이즈 알고리즘
- : 사건 B가 발생한 상태에서 사건 A가 발생할 조건부 확률이다.
- : 사건 A가 발생한 상태에서 사건 B가 발생할 조건부 확률이다.
- : 사건 A가 발생할 확률
- : 사건 B가 발생할 확률
나이브 베이즈 장 단점
- 장점
- 매우 단순하고 결측 데이터가 있어도 우수하다.
- 적은 학습 데이터로도 잘 수행된다.
- 메모리 사용량이 적다.
- 우수한 분류성능을 발휘한다.
- 계산과정의 복잡성이 낮기 때문에 성능이 빠르다.
- 예측에 대한 추정된 확률을 얻기 쉽다.
- 단점
- 모든 속성을 독립적이고 동등하다는 가정에 의존한다.
- 변수들이 확률적으로 독립되지 않은 경우에 오류를 발생할 수 있다.
- 수치속성으로 구성된 데이터 셋에서는 우수하지 않다.
- 추정된 확률은 예측된 범주보다 신뢰가 떨어진다.
주성분 분석
주성분 분석(PCA, Principal Component Analysis)
- 주성분 분석은 고차원데이터(이미지) 분석에서 변수를 선택하거나 변수를 축소하는 기법이다.
- 데이터의 포인트를 가장 잘 구별 해주는 변수인 주성분을 찾는 방법을 의미한다.
- n개의 관측지와 p개의 변수로 구성된 데이터를 상관관계가 없는 k개의 변수로 구성된 데이터로 요약하는 방법이다.
- 요약된 변수는 모든 X변수들의 선형조합으로 생성된다.
- 원래 데이터 분산을 최대한 보존하는 축을 찾고 그 축에 데이터를 사영시킨다.
주성분 분석의 특징
- 주성분은 데이터 포인트가 가장 넓게 분포하는 차원이다.
- 주성분은 자료를 구별하는 것으로 분산이 크면 자료의 차이를 쉽게 구별할 수가 있다.
- X변수의 수가 많은 고차원 데이터를 분석할 경우 변수가 많으면 불필요한 변수가 존재할 수있다. 따라서 주성분 분석은 변수를 축소하기 위한 방법이다.
- PCA는 차원 축소를 통해서 시각화, 압축, 군집화 등을 수행한다.
주성분 분석 예시
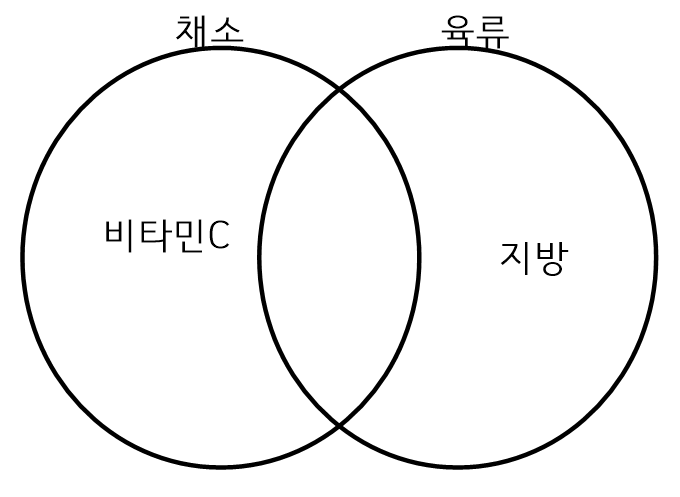
- 위의 예서 식품이라는 변수는 채소와 육류라는 두 개의 집단으로 되어 있다.
주성분 분석은 두 개의 집단을 가장 잘 구분할 수 있는 변수를 찾는 것이다. - 예를 들어 채소는 비타민 C가 다량으로 함유되어 있지만 육류에는 비타민 C가 없다. 그러므로 비타민 C로 집단을 구분하면 채소를 구분 할 수 있다. 마찬가지로 육류에는 지방이 다량으로 함유되어 있지만 채소에는 지방이 없다. 따라서 지방으로 구분하면 육류를 식별 할 수 있다.
- 주성분이라는 말은 어떤 집단을 가장 잘 구분할 수 있는 변수를 의미한다. 이러한 주성분은 데이터 전체에 넓게 흩어져 있다.
주성분 분석과 독립성분 분석
- 주성분 분석
- 데이터 포인트의 분포는 가장 넓은 차원이 유리하다는 것을 가정으로 한다.
- 독립성분 분석
- 데이터 셋에 존재하는 독립 성분을 찾는다.
- 즉, 독립성분에는 데이터의 독특한 정보가 포함되어 있게 된다.
주성분 분석 필요성
| 고차원 데이터 | 주성분 분석의 필요성 |
|---|---|
| 변수의 수가 너무 많다. | 불필요한 변수를 제거한다. |
| 시각화가 어렵다. | 변수의 수를 줄여서 시각화를 한다. |
| 계산의 복잡도가 증가한다. | 분석모델의 비효율성이 증가한다. |
| 중요한 변수들만 선택한다. | 변수의 차원을 축소해야한다. |
주성분 분석기법
변수선택
- 분석모델의 목적에 맞는 최소한의 변수만을 선택하여 분석을 진행한다.
변수선택의 장점과 단점
- 장점
- 선택한 변수를 사용해서 분석을 수행하면 분석 결과에 대한 해석이 용이하다.
- 단점
- 변수가 선택되면 다변량 데이터에서 변수 간의 상관관계를 고려하기 어렵다.
변수추출
- 기존 변수를 변환하여 새로운 변수를 추출한다. 즉, 기존 변수의 결합으로 새로운 변수가 만들어진다.
변수추출의 장점과 단점
- 장점
- 다변량 데이터에서 변수 간의 상관관계를 고려한다.
- 변수의 수를 많이 줄일 수 있다.
- 단점
- 추출 된 변수로 분석된 결과는 해석이 어렵다.
R을 사용한 주성분 분석
iris <- iris
cor(iris[1:4])
is.pca <- prcomp(iris[, 1:4], center=T, scale=T)
is.pca
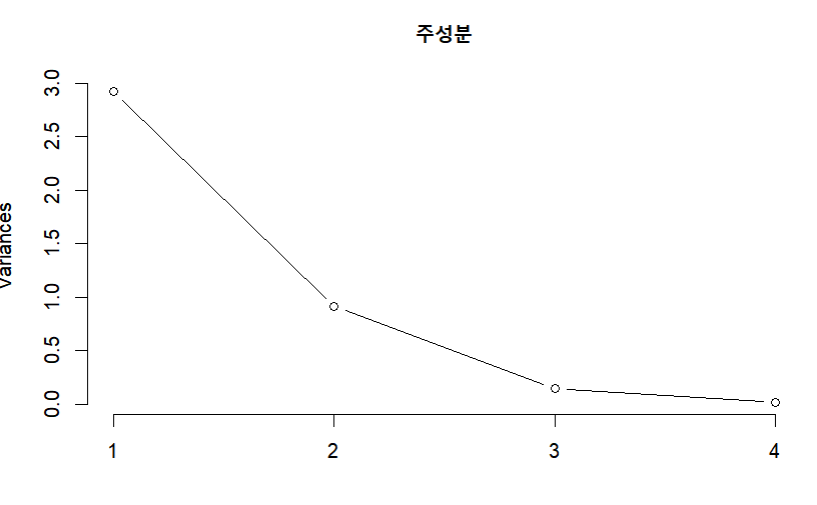
plot(is.pca, type="l", main="주성분")
summary(is.pca)
- proportion of variance 에서 PC1이 전체 분산의 72%을 설명하고 PC2가 22%를 설명한다.
총 PC1과 PC2가 94%를 설명한다.
주성분 분석의 사례
- 사람의 얼굴 인식 하는 기술이 있다.
- 코스피 지수, INDEX 지수 등의 사례가 있다.
신경망
신경망
- 인간의 학습 기능을 모방하는 방법이다.
- 신경망은 데이터 예측의 주요 개념이다.
- 신경망은 인간의 뇌가 패턴을 인식하는 방식을 묘사한 알고리즘으로 이미지, 소리, 문자, 시계열 데이터 등의 패턴을 인식할 수가 있다.
- 신경망은 마치 로지스틱 회귀분석 혹은 다중 회귀분석을 여러 개 연결한 것으로 데이터를 분류하거나 예측할 때 모두 사용될 수가 있다.
신경망의 발전
- 퍼셉트론
- 하나의 신경 세포와 같은 퍼셉트론을 만들어 냈다.
- 하나의 입력에 대해서 처리하고 결과를 출력한다.
- 역전파
- Feedback을 할 수 있도록 해서 퍼셉트론의 결과가 틀린 경우 다시 퍼셉트론으로 입력한다.
- 즉, 결과변수 Y가 틀린 경우 가중치를 조정하여 다시 퍼셉트론에 입력하면서 학습을 수행한다.
최근 신경망이 이슈되는 이유
- 컴퓨터 처리능력 향상으로 1000억개의 신경을 만들지 않아도 인간처럼 처리능력이 향상되었다.
활용
- 금융회사의 고객관리
- 주식의 가격을 시계열 예측
- 생산공정 관리
- 기업과 개인의 파산의 예측
- 의학적 진단
- 안면인식
- 자율주행
신경망의 장단점
- 장점
- 예측 성능이 우수하다.
- 변수들 사이의 복잡한 관계를 우수하게 파악할 수 있다.
- 데이터에 잡음이 많아도 좋은 성능을 낸다.
- 단점
- 결과에 대한 해석이 어렵다.
- 복잡한 학습과정으로 모형 구축에 많은 시간이 걸린다.
- 학습을 위해서는 많은 양의 데이터가 필요하다.
신경망
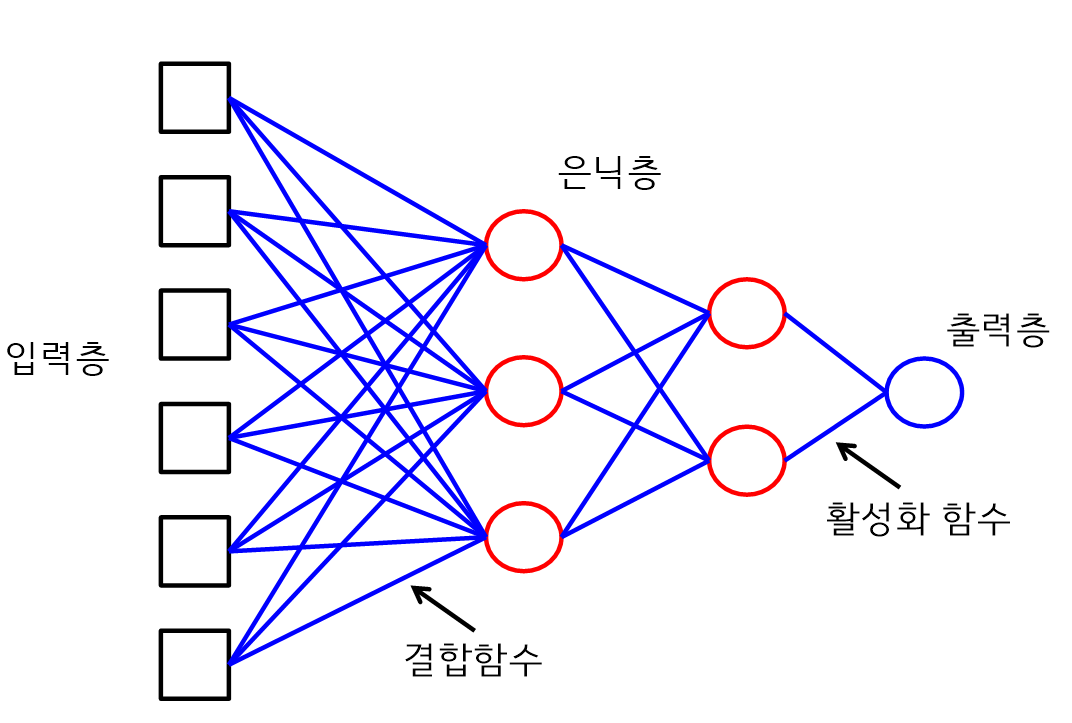
- 결합함수는 입력층 또는 은닉층의 마디들을 결합하는 것으로 선형함수이다.
- 결합함수는 선형함수이다.
퍼셉트론
-
퍼셉트론은 하나의 신경망에 해당되는 것으로 입력값의 데이터가 임계치를 넘으면 다른 퍼셉트론에 결과를 전송한다.
즉, 인간의 세포도 입력값을 받고 다른 세포에 전달할지를 결정한다. -
퍼셉트론은 다수의 입력값과 가중치를 선형으로 결합하여 계산한다.
-
활성화 함수에 따라서 생성되는 출력값이 결정된다.
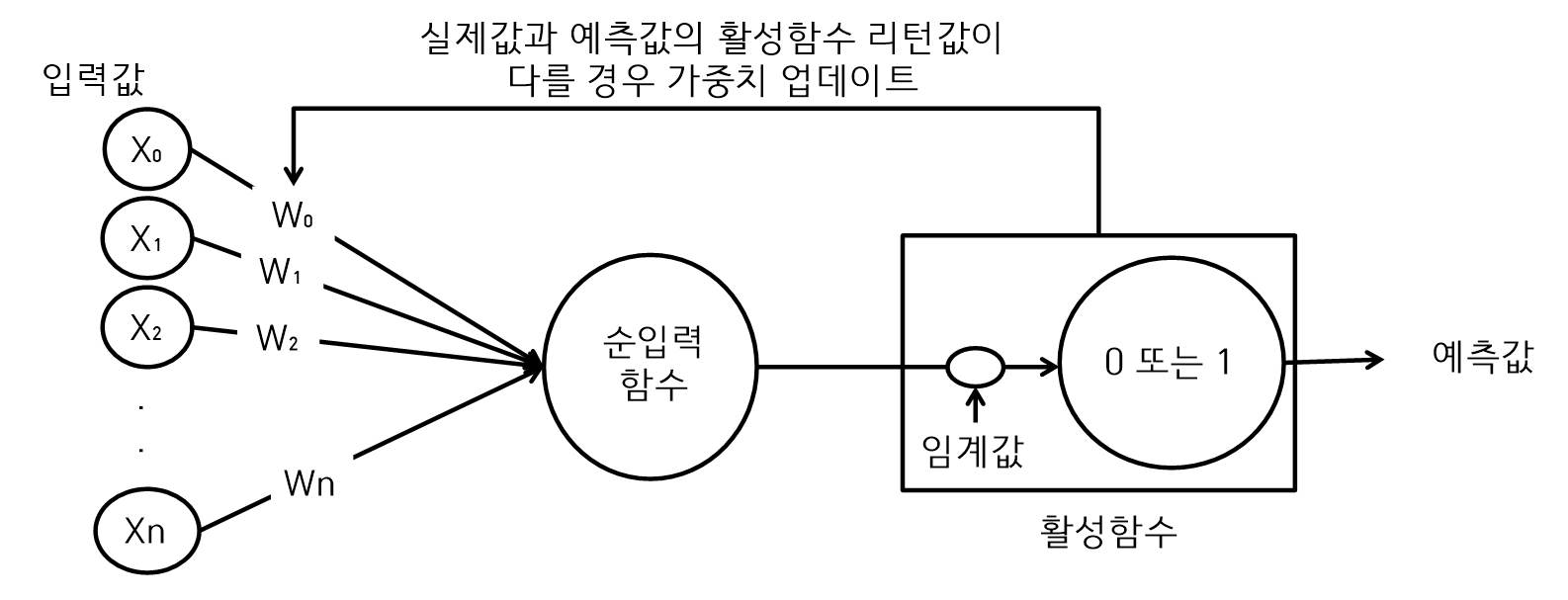
-
~ 은 퍼셉트론 알고리즘의 입력값이다.
-
~ 은 ~ 에 곱해지는 가중치 값이고 모든 가중치와 을 곱한 결과는 모두 더해서 하나의 결과값을 만든다.
신경망은 가중치 값을 사용해서 출력을 조절한다. -
활성함수는 최종 결과값을 다른 퍼셉트론에게 데이터로 전달할 것인지 전달하지 않을 것인지를 결정하는 것으로 로지스틱 회귀모델에서는 S Curve인 시그모이드 함수를 사용한다. 하지만 신경망에서는 다양한 함수를 사용할 수가 있다.
-
학습이란 결과적으로 ~ 을 찾아내는 과정이다.
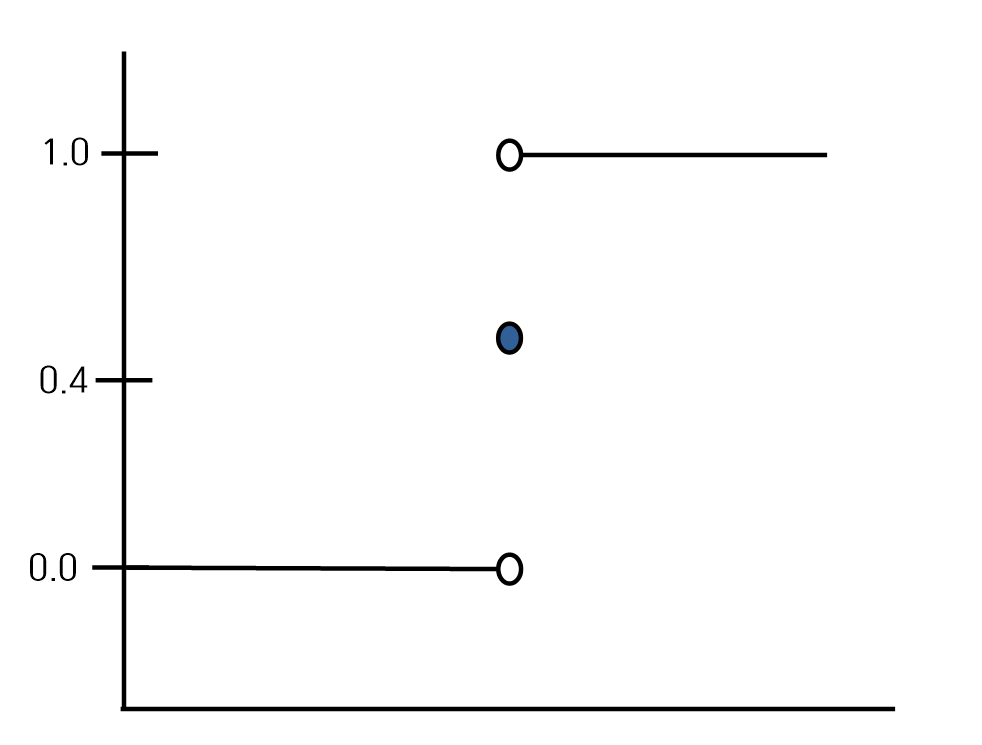
활성화 함수
- 활성화 함수는 어떤 신호를 받아서 적절한 처리를 하고 출력하는 함수이다.
- 결과값은 0 혹은 1로 나온다. 1이면 다른 퍼셉트론에게 그 결과값을 전달하고 0이면 전달하지 않는다.
- 활성화 함수를 사용해서 출력된 신호가 다음 단계에서 활성화 되는지를 결정한다.
- 활성화함수는 신호를 입력 받아서 처리하고 출력하는 함수이다.
활성화 함수
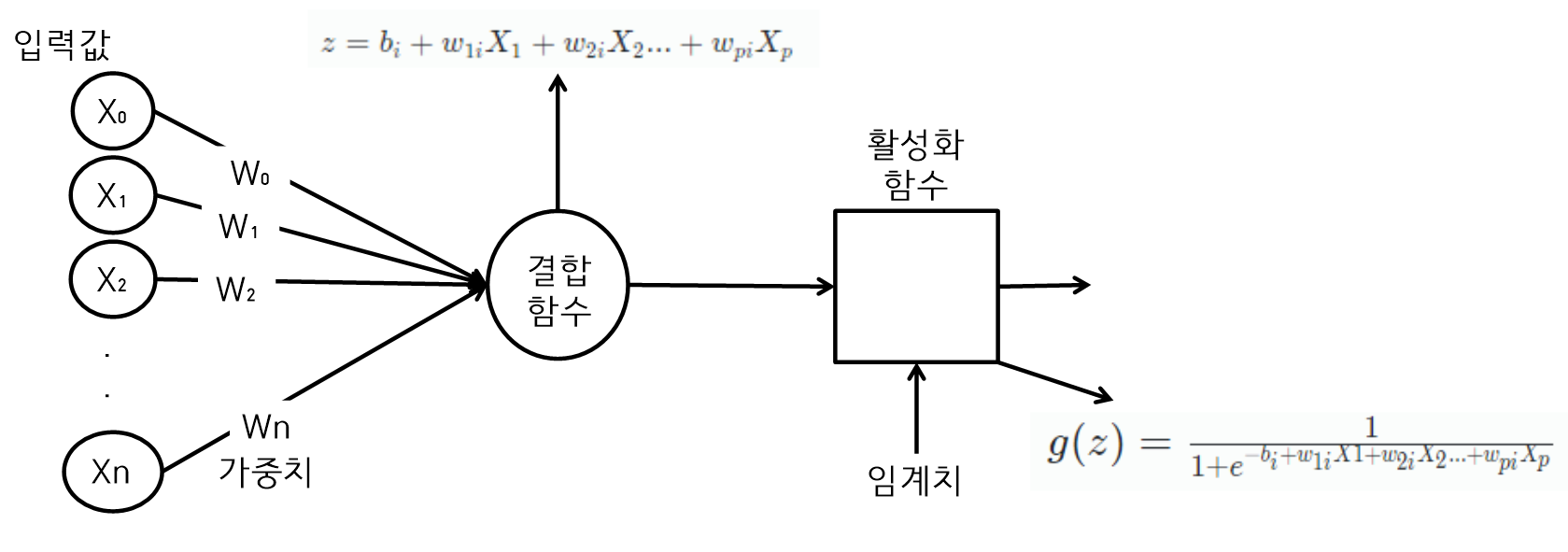
활성화 함수
Input data -> {Activation Fuction} -> Output data
Step function
- 각 부분구간 내에서 상수함수이며 부분구간 경계에서 불연속적인 함수이다.
- Step function
-
Sigmoid function
- Sigmoid function은 출력이 0과 1만 가질 수 있는 비선형 함수이다.
- Sigmoid 함수는 0과 1사이의 값을 부드럽게 만들어 준다.
- 로지스틱 회귀분석에서 사용된다.
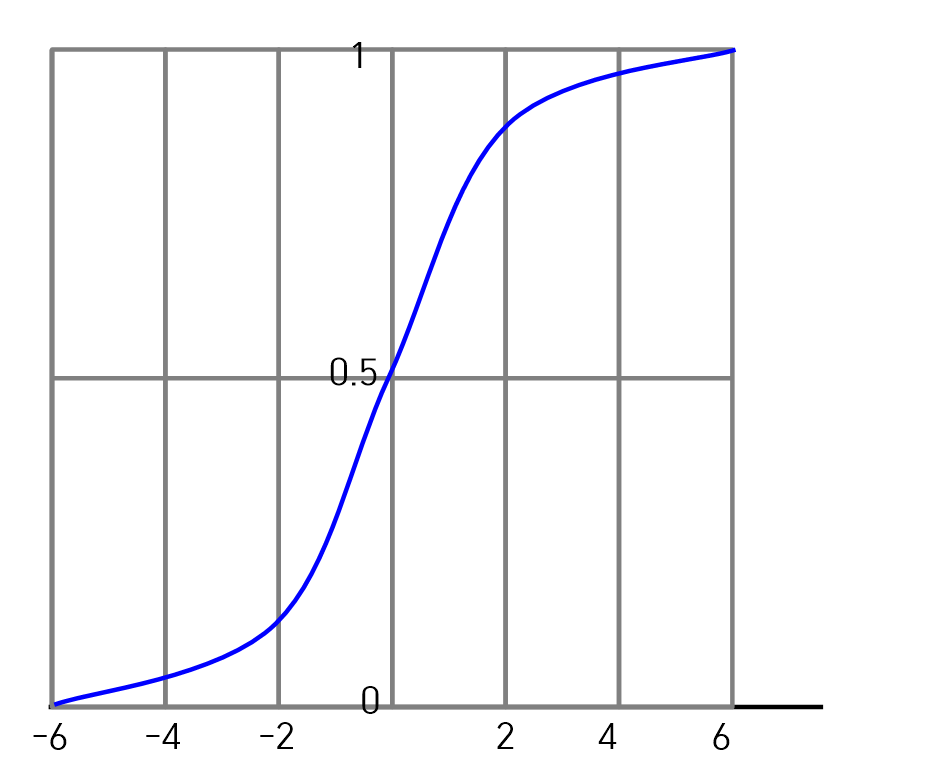
- Sigmoid function
ReLU(Rectified Linear Unit) function
- 선형함수로 최근에 가장 많이 사용하고 있는 활성화 함수이다.
- Sigmoid function의 Gradient Vanishing 문제를 해결하기 위해서 ReLU를 사용한다.'
- ReLU 함수는 딥 런닝에서 많이 사용된다.
- Gradient Vanishing
- Sigmoid function은 0과 1 사이의 출력값을 가질 때 0에 매우 가까운 값을 가지게 되는 것이다. 예로 0.0001과 같은 출력을 말한다.
- Back-Propagation시에 각 Layer를 많이 통과하면 결국 0으로 수렴하는 문제이다.
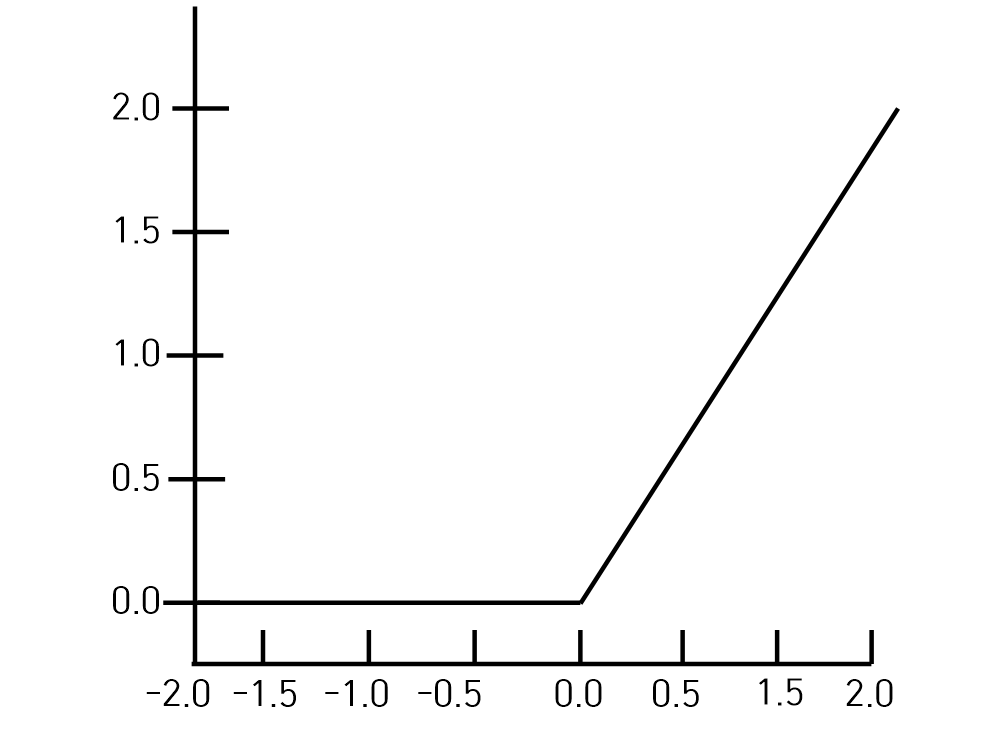
- ReLU function
기타 활성화 함수 종류
- Sigmoid
- Leaky ReLU
- tanh
- ReLU
- Maxout
- ELU
신명망의 종류
단층 퍼셉트론
- 최초의 퍼셉트론은 단층 퍼셉트론으로 N개의 입력에 대한 은닉계층 없이 바로 출력되는 구조이다.
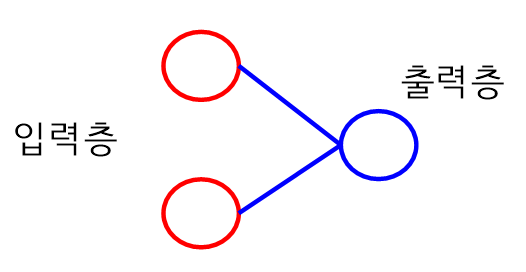
다층 퍼셉트론
- 입력계층과 출력계층 사이에 은닉계층이 존재한다.
- 출력계층에서 softmax함수를 사용하여 가장 큰 값을 알 수 있다.
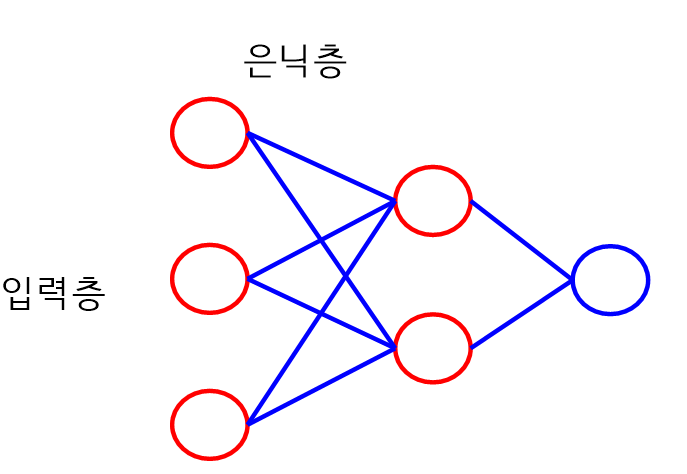
딥러닝
- 다층 퍼셉트론을 수천개 이상을 연결하여 학습한다.
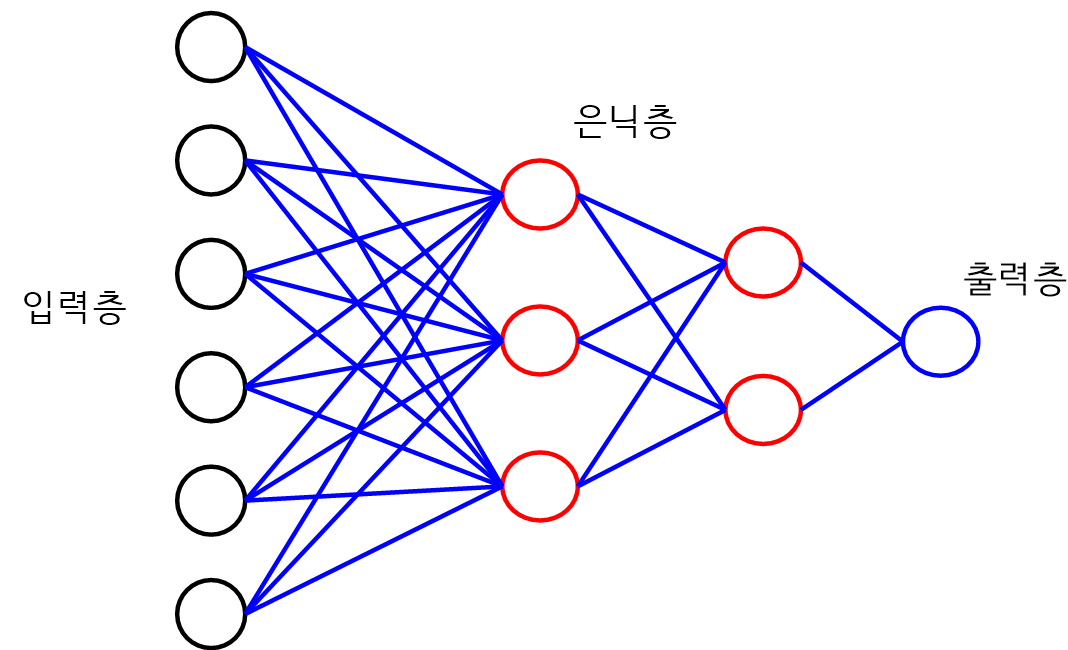
Back-propagation(역전파 알고리즘)
- 신경망에서 학습이란 예측결과를 찾기 위해 연결강도인 임계치, 가중치를 찾는 것이다.
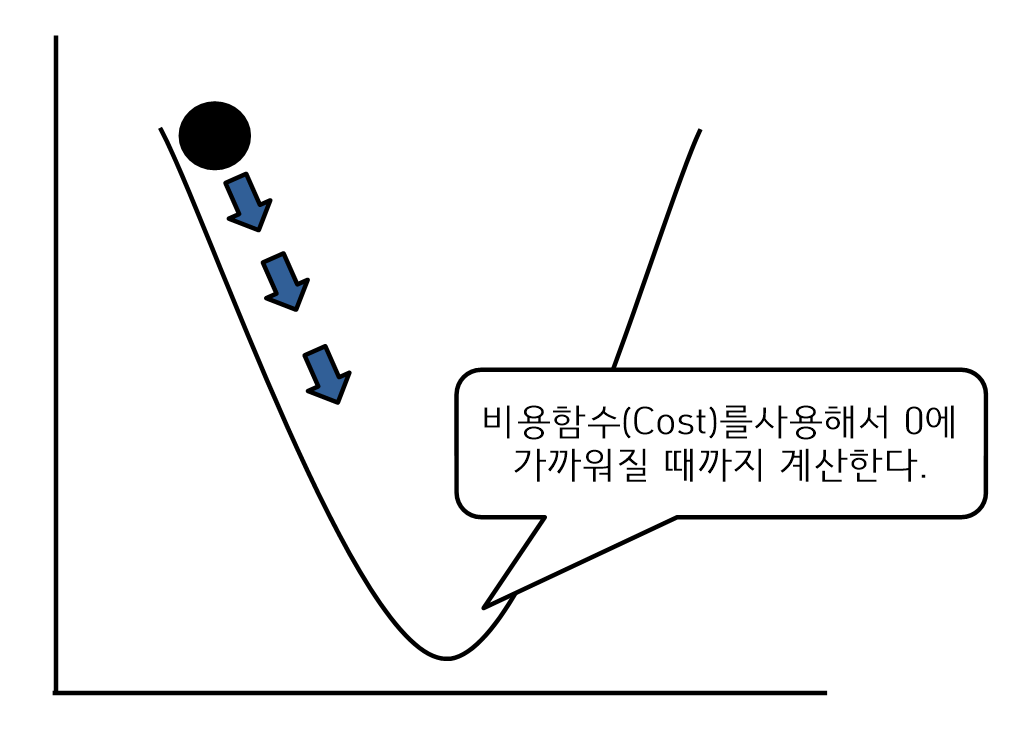
- 비용함수, 손실함수는 에러를 최소화하기 위해서 비용이 0에 가까운 시점을 찾는 것이다.
- Back-propagation은 비용 값이 0이 되도록 가중치를 조정하여 다시 입력 값으로 전송한다.
- 경사하강법(비용이 0에 가까운 시점을 찾는것)
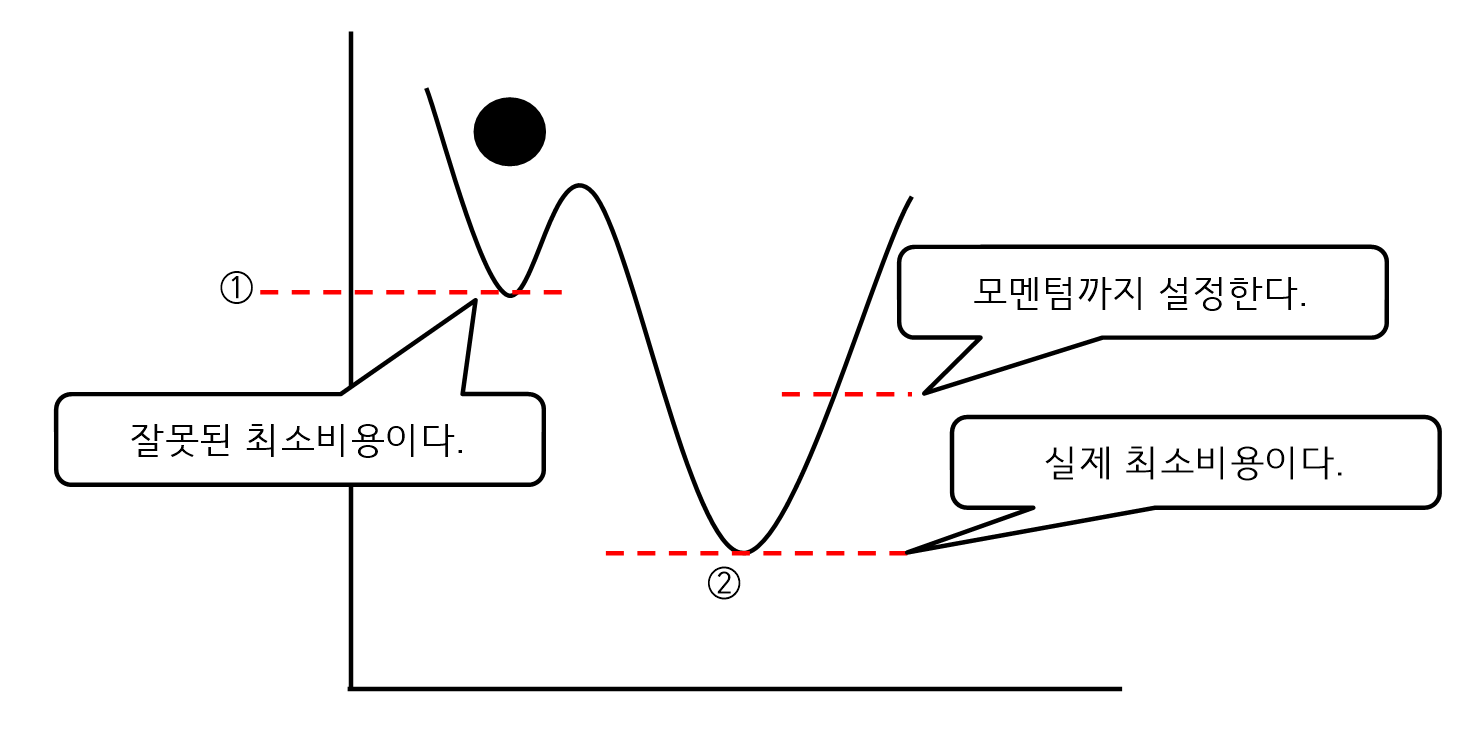
- 최소비용을 찾으려고 ①까지 탐색을 한 후에 최소비용을 설정하는 오류가 발생 할 수 있다.
- 이를 위해서 어느 시점까지 계속 탐색하게 하는 모멘텀을 설정해야 한다.
- 즉, 모멘텀은 어느 정도 기존의 방향을 유지할 것인지를 조정하는 것이다.
신경망 알고리즘 사례
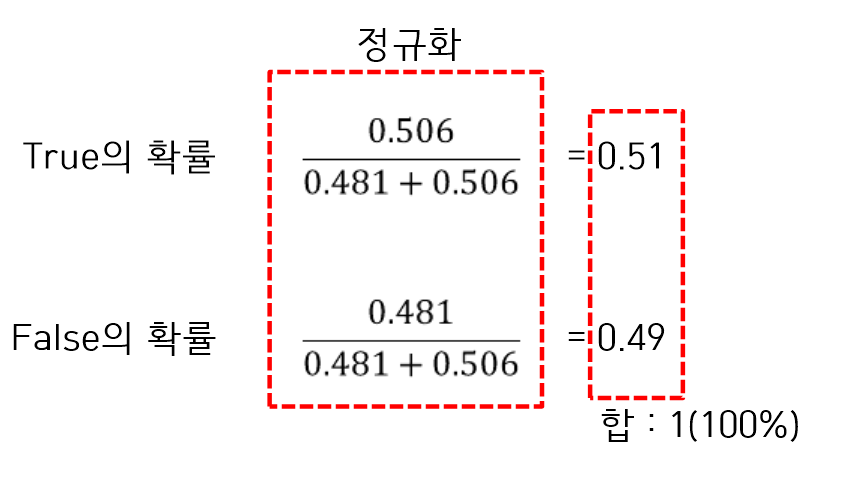
- 최종 결과값에 대한 Cut-off는 0.5로 정의한다. 즉, 0.5보다 값이 크면 True이고 0.5보다 작으면 False이다.
- 활성화 함수는 Sigmoid 함수를 사용한다.
신경망 알고리즘
신경망(1)
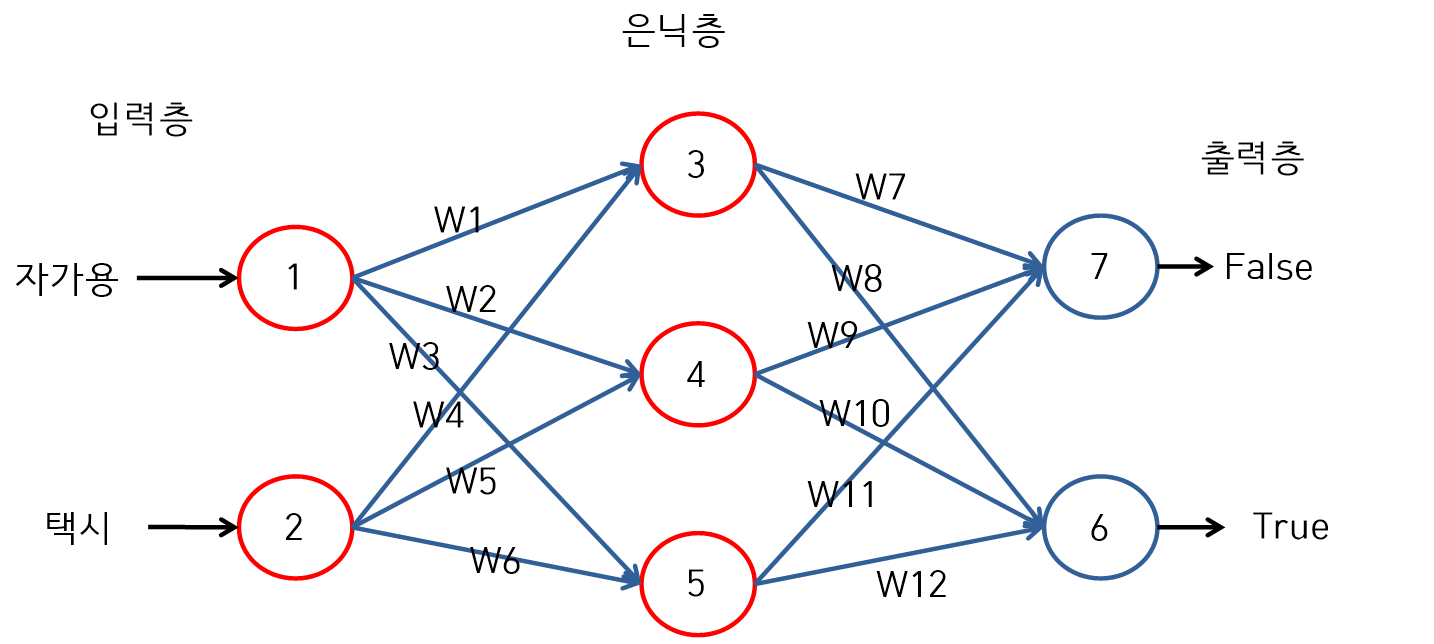
신경망(2)
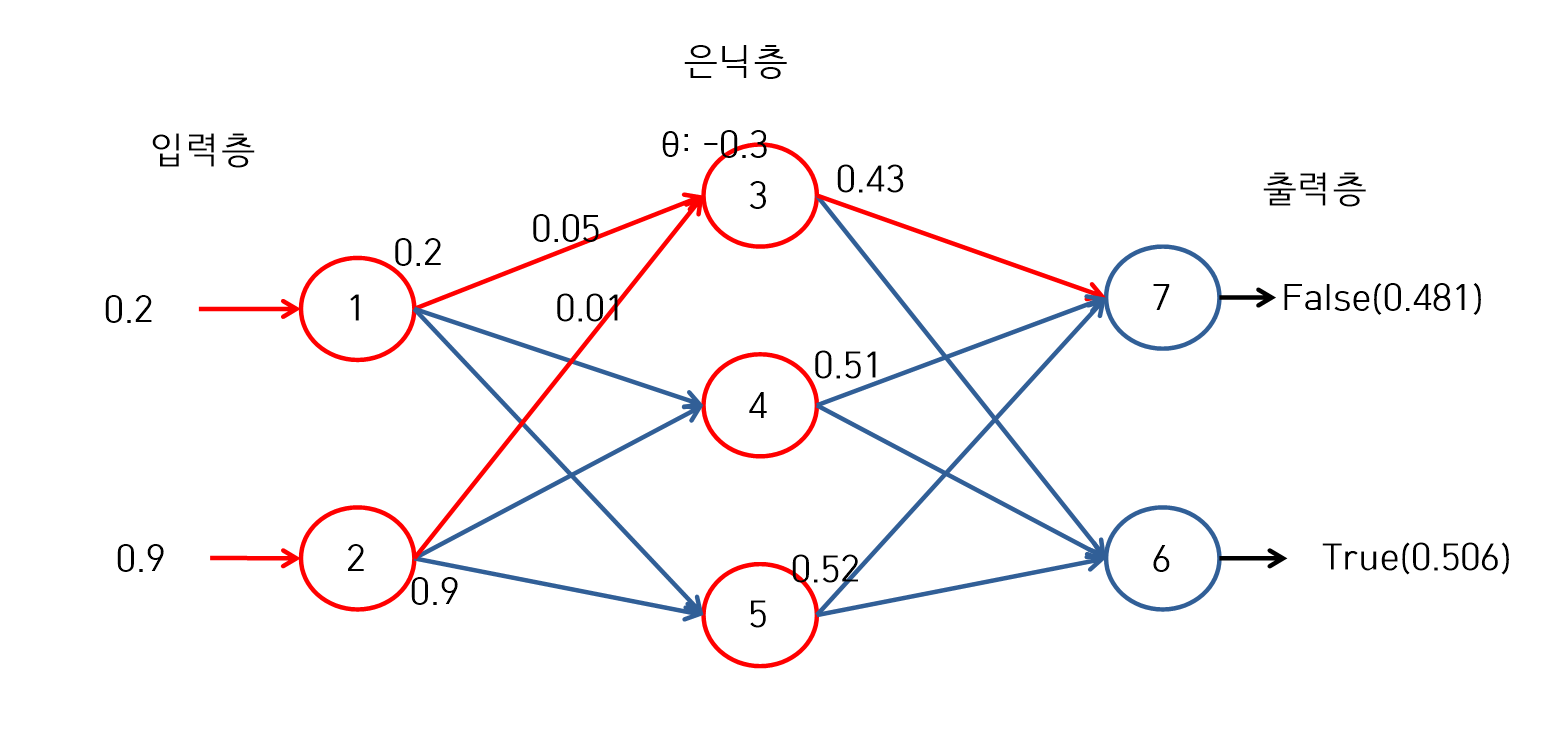
신경망(3)
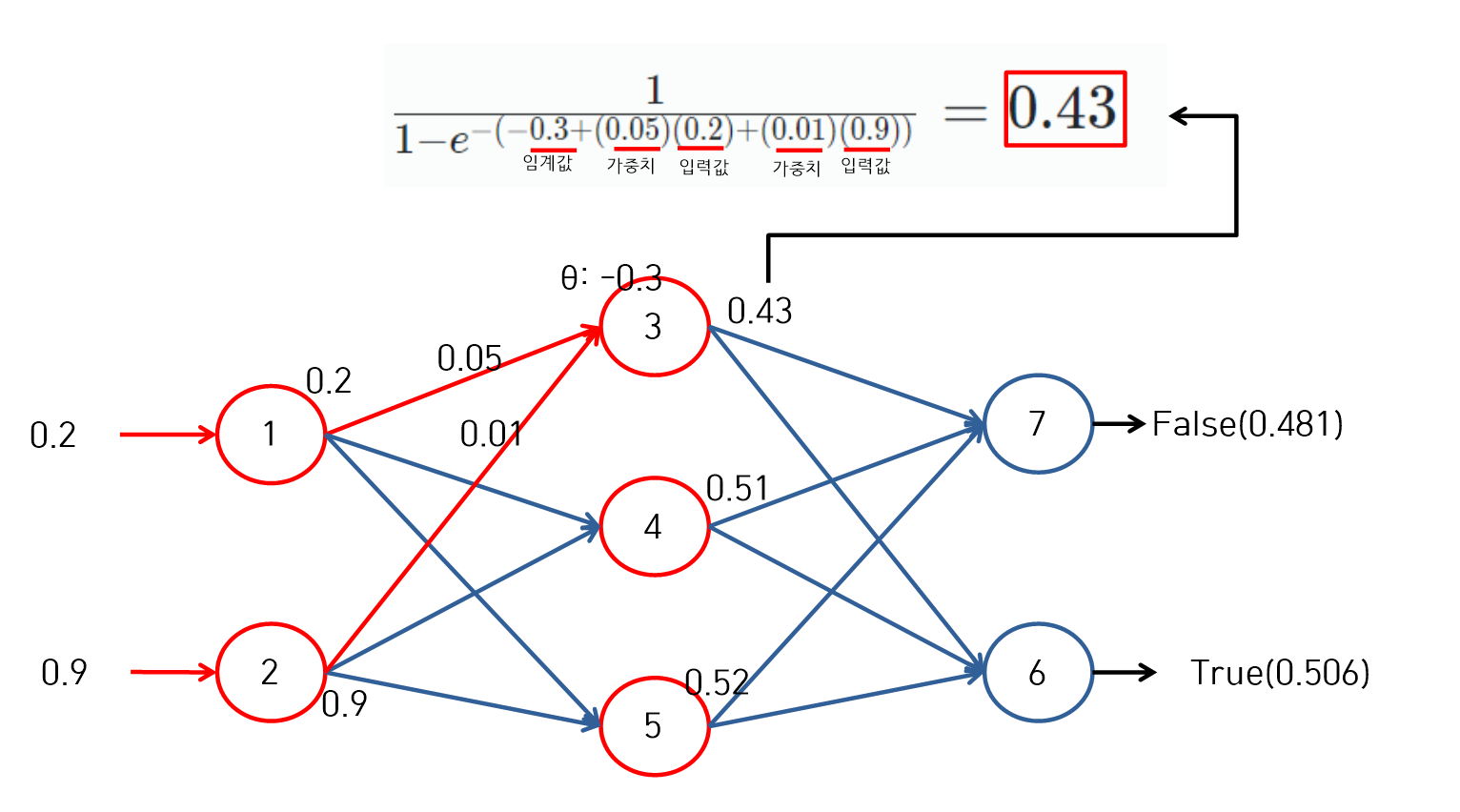
신성망(4)
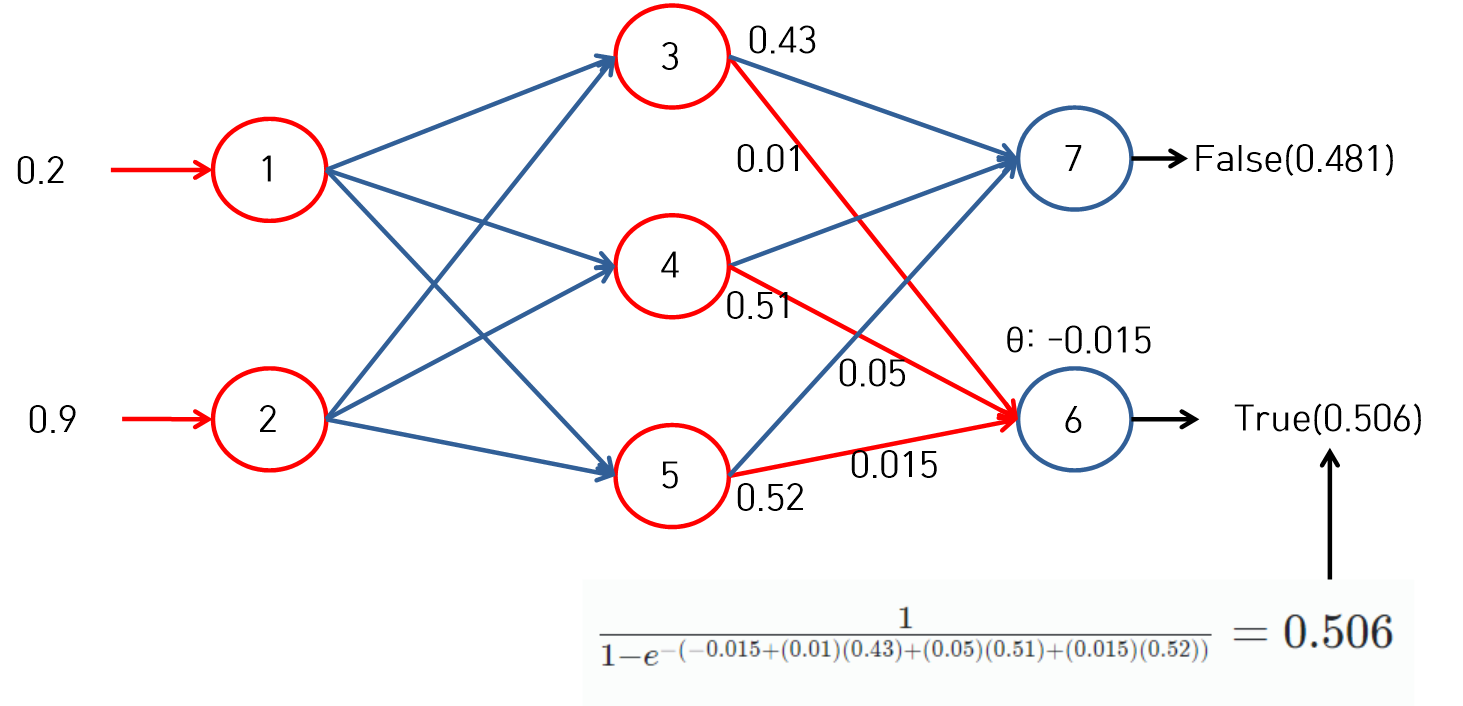
- 최종결과 0.506이 True이고 False는 0.481이다. 이 값을 정규화 하여 1의 값으로 맞추어 준다.
신경망(5)
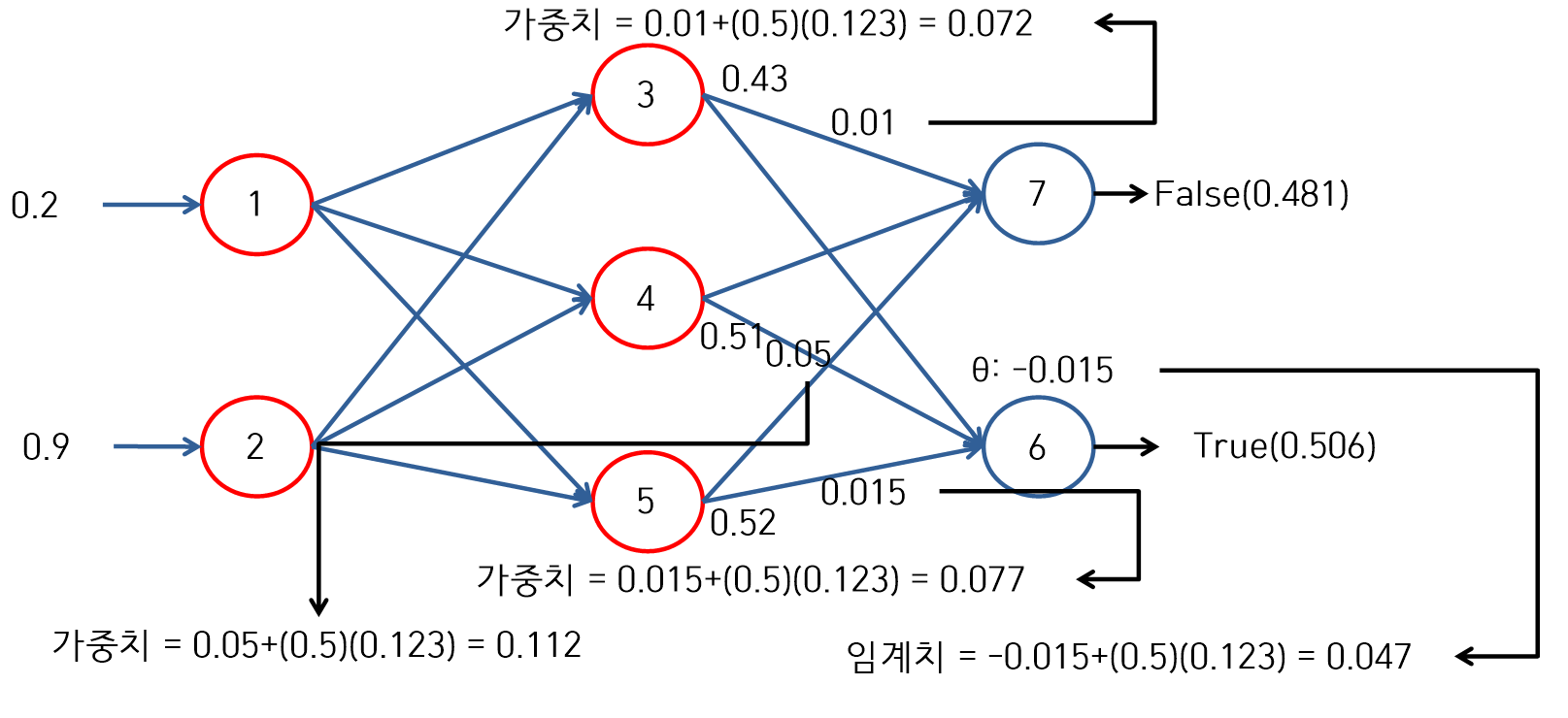
Back-propagation
- 에러를 계산해서 오차를 역추적한다. 즉, 에러를 계산하고 에러를 낮추기 위해 임계치와 가중치를 조정해서 다시 입력층으로 입력한다.
에러 계산
- True에 대한 에러 = (0.506)(1-0.506)(1-0.506) = 0.123
- False에 대한 에러 = (0.481)(1-0.481)(1-0.481) = 0.129
가중치 조정
- 에러 값을 사용해서 임계치와 가중치를 설정한다.
신경망의 문제점
대표적인 단점
- 결과에 대한 해석이 어려운 Black box model이다.
- 학습 완료 시점을 예측할 수 가 없다.
- 학습이 완료될 때까지 많은 회수의 반복학습을 해야 한다.
- 추가 학습이 발생하면 전체적으로 재학습 해야 한다.
신경망의 포화상태와 과대적합
- 포화는 신경망에서 학습하면 할수록 활성화 함수에서 만들어질 수 가 없는 더 큰 결과값을 만들기 위해서 더 큰 가중치를 시도하게 되므로 신경망이 포화가 되게 된다.
과대적합
- 분석모델이 훈련 데이터에 잘 맞지만 일반성이 떨어진다.
- 훈련 데이터에 대해서만 높은 성능을 보여준다.
과소적합
- 분석모델이 너무 단순해서 데이터의 내재된 구조를 학습하지 못할 때 발생한다.