확률

확률

• 확률은 어떤 사건이 발생할 가능성으로 0과 1사이의 숫자로 표현
• 표본 자료를 사용해서 구한 통계량과 모집단의 모수를 추론

추리통계학은 확률
통계학은 전수조사를 할 수가 없어서 표본조사를 한다. 표본조사는 표본오차를 발생시킨다.
표본오차는 모집단의 모수와 표본 간에 발생하는 오차

모수
표본 관측으로 구하고자 하는 모집단에 대한 정보

확률의 정의

• 고전적
  • 이론적인 확률을 의미
• 경험적
  • 실험을 통해서 얻어진 확률
  • 예를 들어 어느 제품을 제작할 때 발생될 수 있는 불량율
• 주관적
  • 전문가의 의견으로 주관적으로 판단되는 확률
  • 객관적으로 판단될 수 있는 확률

확률계산

• 확률계산은 전체경우의 수와 사건이 발생할 수 있는 경우의 수(A)로 계산된다.

• 확률계산(중요)
  $확률 = \frac{사건이 발생할 경우의 수}{전체경우의 수}$

  $P(A) = \frac{n(A)}{n(S)}$

• P(A) : 사건 A가 일어날 확률이다.

• n(A) : 사건 A가 일어날 수 있는 경우의 수

• n(S) : 전체 경우의 수, S는 표본공간을 의미

표본공간

• S로 표시하며 통계적 시험에서 발생할 수 있는 경우의 수

사건

• 특정 결과가 발생하는 모임으로 A, B, C 등으로 표현

카운팅과 규칙

• 카운팅은 사건이 발생할 수 있는 경우의 수를 계산
• 카운팅은 곱셈의 법칙을 사용해서 카운팅을 계산
• k번 실험의 결과 집합은 $n_1\times n_2\times n_3\times n_k$가 된다.

카운팅 방법

문제1. 사장 10명과 사원 3명, 대리 5명이 근무하는 경우 
	 각 대표를 1명으로 총 3명의 위원회가 열릴 경우의
     수는 무엇인가? 
  답1. 사장단에서 10명, 사원에서 3명, 대리급에서 5명이 나올 수 있음으로
     10 * 3 * 5 가 되어 150의 경우의 수가 나온다.


문제2. 남자 4명과 여자 5명이 만날 때 짝이 될 수 있는 
	  경우의 수는 무엇인가?
 답2. 남자 4명, 여자 5명이 각각 짝을 지을 수 있으므로 4 * 5가 되어
      경우의 수가 20이 된다.

순열

• 서로 다른 n개 중 r개의 선택해서 순서를 고려한 후 나열하는 방법의 수
• n Factorial을 사용한다. 예를 들어 5개 영화가 있을 때 순서적으로 영화를
  청취하는 경우 중복 없이 청취하는 경우는 $5! = 5 * 4 * 3 * 2 * 1$이 된다.
• Factorial
  $n! = n(n-1)(n-2)....(1)$

조합

• 서로 다른 n개의 원소에서 순서에 관계없이 r을 뽑는 경우 이를 n개에서 r개를 선택하는 조합이라고 한다.
• 조합
  $_{n}C_{r} = \frac{n!}{r!(n-r)!}$

추리통계

• 추리 혹은 추론통계는 기술적 통계에서 자료의 특성이 분석되면 표본을 사용하여 모집단의 특성을 추정하는 분석이다.
• 통계분석과정
  

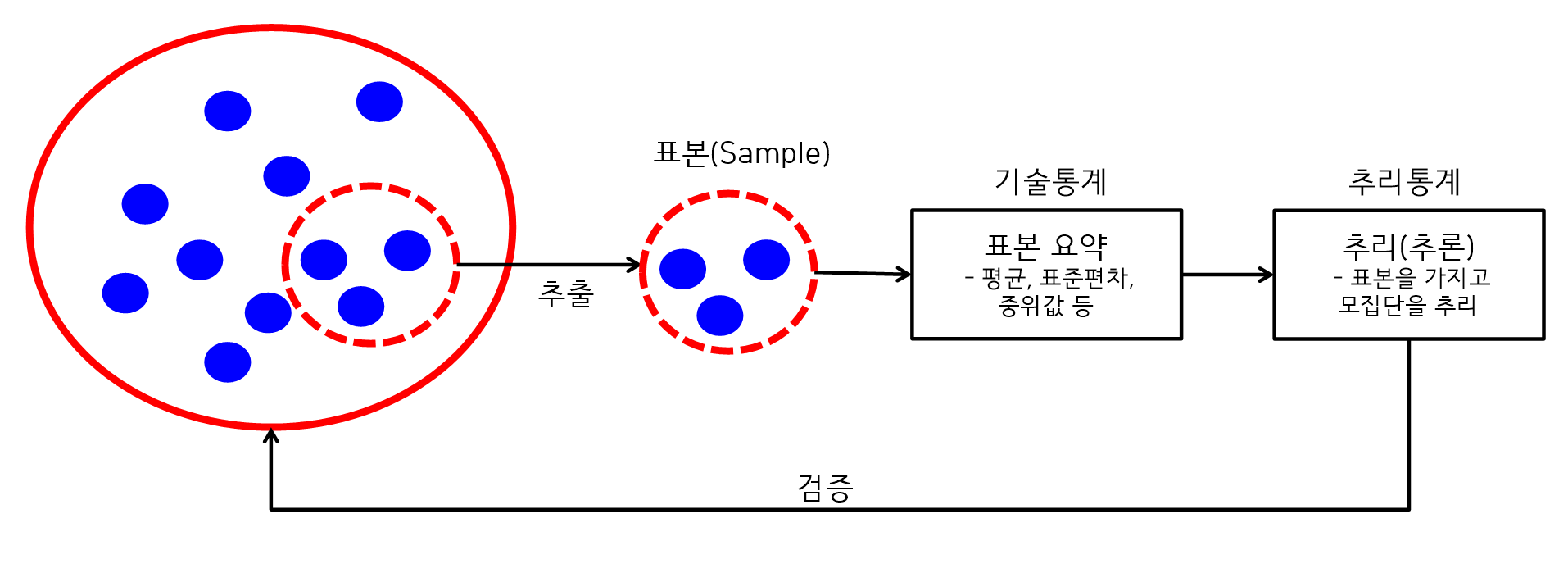
기술통계와 추리통계 차이점

• 기술통계는 자료를 요약하는 것이고 추리통계는 표본을 사용해서 모집단의 특성을 추정하는 것이다.

  기술통계	추리통계
  수집한 데이터의 특성을 파악하기 위해서 요약정리하는 통계방법	수집한 데이터에서 표본을 추출하여 전체 모집단의 특성을 추정하여 미래를 예측하는 것
  평균, 중위값, 최빈수, 범위, 분산, 표준편차와 같은 분석으로 데이터의 특성을 파악	차이검정 및 관계검정 등

추리통계학 작업

• 가설형태
• 통계적 결정오류 및 통계적 유의도
• 가설검증

• 추리통계에 대한 검증 방법은 모수에 의한 검증, 비모수 통계 검증으로 구분할 수 있다.
  이 중에서 모수통계 검증 방법은 T-test, ANVOA, Z 검증 방법이 있으며 비모수 통계 검증 방법은 $X^2$검증, Mann-Whitney U 검증, Kruskal-Wallis 검증 등이 있다.