최소직사각형

문제설명

명함 지갑을 만드는 회사에서 지갑의 크기를 정하려고 합니다. 다양한 모양과 크기의 명함들을 모두 수납할 수 있으면서, 작아서 들고 다니기 편한 지갑을 만들어야 합니다. 이러한 요건을 만족하는 지갑을 만들기 위해 디자인팀은 모든 명함의 가로 길이와 세로 길이를 조사했습니다.

아래 표는 4가지 명함의 가로 길이와 세로 길이를 나타냅니다.

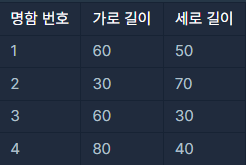
가장 긴 가로 길이와 세로 길이가 각각 80, 70이기 때문에 80(가로) x 70(세로) 크기의 지갑을 만들면 모든 명함들을 수납할 수 있습니다. 하지만 2번 명함을 가로로 눕혀 수납한다면 80(가로) x 50(세로) 크기의 지갑으로 모든 명함들을 수납할 수 있습니다. 이때의 지갑 크기는 4000(=80 x 50)입니다.

모든 명함의 가로 길이와 세로 길이를 나타내는 2차원 배열 sizes가 매개변수로 주어집니다. 모든 명함을 수납할 수 있는 가장 작은 지갑을 만들 때, 지갑의 크기를 return 하도록 solution 함수를 완성해주세요.

제한사항

• sizes의 길이는 1 이상 10,000 이하입니다.
  • sizes의 원소는 [w, h] 형식입니다.
  • w는 명함의 가로 길이를 나타냅니다.
  • h는 명함의 세로 길이를 나타냅니다.
  • w와 h는 1 이상 1,000 이하인 자연수입니다.

입출력 예

입출력 예 #1
문제 예시와 같습니다.

입출력 예 #2
명함들을 적절히 회전시켜 겹쳤을 때, 3번째 명함(가로: 8, 세로: 15)이 다른 모든 명함보다 크기가 큽니다. 따라서 지갑의 크기는 3번째 명함의 크기와 같으며, 120(=8 x 15)을 return 합니다.

입출력 예 #3
명함들을 적절히 회전시켜 겹쳤을 때, 모든 명함을 포함하는 가장 작은 지갑의 크기는 133(=19 x 7)입니다.

나의 풀이

명함의 사이즈를 다 담을 수 있는 아주 쉬운 것은 가장 큰 수 2개를 뽑아 그 수만큼의 지갑을 만드는 것이다.
그러나 문제에서는 제일 큰 명함을 담을 수 있는 최소한의 지갑크기로 만든다고 했다.
명함은 가로, 세로 바꿀 수 있다는 것을 착안하여 문제를 풀었다.

• 명함을 전부 가로가 가장 큰 쪽으로 다 돌린다.
• 명함의 가로방향에서 가장 큰 수, 세로방향에서 가장 큰 수를 뽑아서 지갑을 만들면 된다.

코드로 표현하면 다음과 같다.

function solution(sizes) {
    //가로방향의 가장 큰수를 담기위한 변수
    let first_index = [];
    //세로방향의 가장 큰수를 담기위한 변수
    let second_index = [];
    //명함의 갯수만큼 반복을 돌려 명함들을 가장 큰수가 가로로 오게 정렬한다.
    for (let i = 0; i < sizes.length; i++) {
        sizes[i].sort((a,b) => b-a);
    }
    //명함을 정렬했다면 이번에는 가로방향과 세로방향의 크기들을 배열에 담는다.
    for (let i = 0; i < sizes.length; i++) {
        for (let j = 0; j < sizes[0].length; j++) {
            first_index[i] = sizes[i][0];
            second_index[i] = sizes[i][1];
        }
    }
    //각각의 가로와 세로를 가장 큰수가 앞에오게 정렬하여
    first_index.sort((a,b) => b - a);
    second_index.sort((a,b) => b - a);
    //가장 큰 수를 각각 곱하면 최소직사각형의 너비가 나온다.
    return first_index[0] * second_index[0];
}

다른 사람의 풀이

문제의 접근은 같지만 코드의 효율이 좋다.
본인은 for문의 for문을 사용하면서 불필요한 반복 행위가 다소 많이 일어나는 한편 아래의 코드는 반복을 한번만 하고 나머지는 배열의 정렬만을 사용하여 문제를 해결하였다.

function solution(sizes) {
    //명함의 사이즈들을 가장 큰수가 0번째 index에 오도록 정렬한다.
    for (let size of sizes) {
        size.sort((a, b) => a - b);
    }
    //sizes의 0번째 index들를 큰 수 부터 정렬하고 0번째 배열의 0번째 인덱스를 a변수에 넣는다.
    const a = sizes.sort((a, b) => b[0] - a[0])[0][0];
    //sizes의 1번째 index들를 큰 수 부터 정렬하고 0번째 배열의 1번째 인덱스를 b변수에 넣는다.
    const b = sizes.sort((a, b) => b[1] - a[1])[0][1];

    return a * b;
}