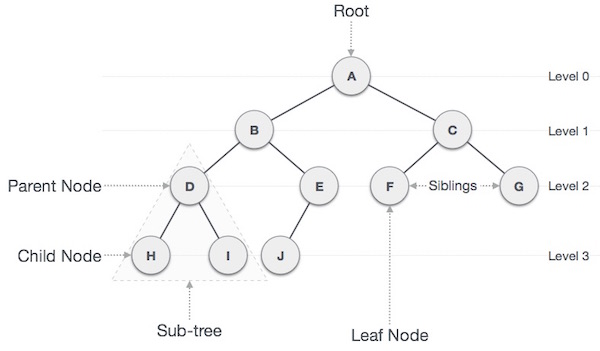
데이터의 상하관계를 저장하는 자료구조이다. 나무모양을 해서 트리구조인 것 같다.
그림에 나와있듯이 맨 위 시작이 되는 node를 Root라고 하고 특정 node에서 파생된 node를 child node.
child node의 상위 노드를 parent node, 그리고 같은 부모를 가지는 자식노드들을 묶어 sibling.
더 이상 자식요소를 가지지 않는 node(말단 node)를 leaf 라고 한다.
(뭐 잎사귀도 있겠다. 걍 나무다 나무 )
정리하면
- Root => A
- Parent => A, B, C, D, E
- Child => B, C, D, E, F, G, H, I, J
- Leaf => H, I, J, F, G
- Sibling => (B,C) (D,E) (F,G) (H,I)
컴퓨터 폴더구조나 HTML의 Dom 트리구조가 트리로 되어있다.
트리는 Graph의 한 종류라고 할 수 있다. (사실 자료구조의 대부분이 그래프의 한 종류이다.)
그리고 일전에 다룬 linked list는 트리의 한 종류이다.
Binary Tree (이진트리)
이진트리란 자식노드가 최대 두 개(0,1,2개를 가질 수 있다는 말)인 노드들로 구성된 트리이다.
이진트리에는 full binary tree, complete binary tree, balanced binary tree perfect Binary tree 등이 있다.
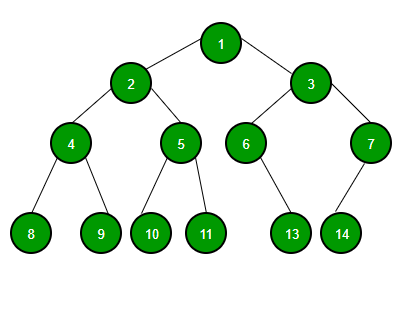
장점: Better than O(n), ordered, Flexible Size
단점: No O(1) operations
Perfect Binary tree
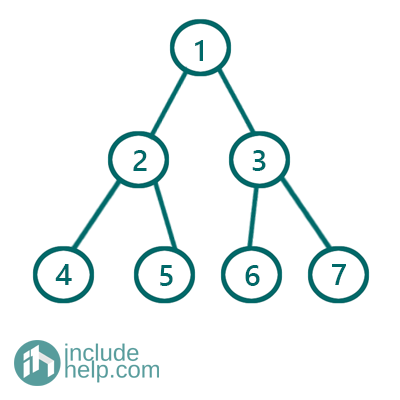
모든 leaf 노드가 차있고 1개의 자식노드만 가지고 있는 노드가 없는 트리, 모든 마지막 노드는 자식노드가 없는 트리이다.
- 자식노드는 꼭 부모의 2배로 증가한다.
- 마지막 자식노드 개수의 합은 무조건 나머지 노드들의 갯수 +1 이다.
이러한 특징 때문에 perfect binary tree는 lookup, insert, delete에서 O(logN)의 시간 복잡도를 가진다.
Full Binary tree
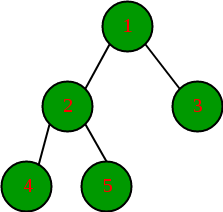
모든 노드가 0개 혹은 2개의 children 을 가지고 있는 Binary Tree.
모든 leaf 노드의 개수는 leaf가 아닌 node 의 개수 + 1 이다.
Complete Binary tree
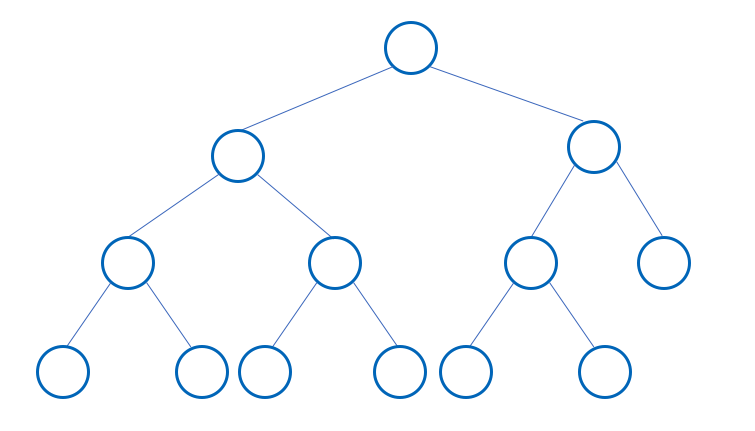
마지막 level 을 제외한 나머지 level 에 node 들이 가득 차있고, 마지막 level 에서 node 는 가장 왼쪽 부터 채워지는 형태의 이진트리
구조를 그대로 사용하여 Binary Heap 이라는 데이터 구조를 만들 수 있다.
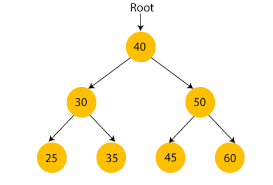
Binary Search Tree (이진탐색트리)
이진탐색트리란 이진탐색(binary search)과 연결리스트(linked list)를 결합한 자료구조. 이진탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안됐다.
종속 데이터들 간의 상하관계를 보존하고 logN의 시간복잡도를 가지고 있어서 Hash보다 좋은 search 방법이다.
단 여기 규칙이 있는데
1 . 모든 오른쪽 자식노드는 부모보다 값이 커야한다.
2 . 0이나 2개의 자식노드만 가질 수 있다.
위 규칙을 지치면 lookup은 logN의 시간복잡도를 가지지만 insert, delete도 logN이라 hash보다 빠르지는 않다.
Balance vs Unbalanced Tree
인터뷰 질문으로 나오는 부분이다. 적어도 강의에서는 그랬다.
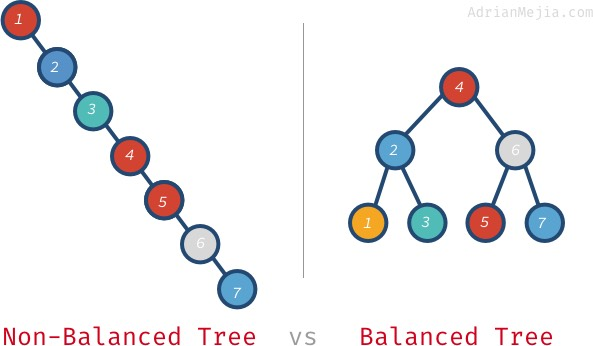
자 이진탐색 트리구조로 data가 짜여지면 O(logN)이라는 이상적인 상황이 나오지만 계속 가장 큰 값이 insert 된다면 시간복잡도는 O(n)로 느려지게 된다.
가장 큰값이 계속 append되는 상황이면 위처럼 한쪽으로만 긴 Unbalanced tree가 되고 결국 시간복잡도는 O(n) 되어 트리의 장점이 사라진다.
참고
Udemy " Master the Coding Interview: Data Structures + Algorithms " - Zero To Mastery
