Trees 트리 (2)

BST (Binary Search Tree)만들기

class Node {
  constructor(value){
    this.left = null;
    this.right = null;
    this.value = value;
  }
}

class BinarySearchTree {
  constructor(){
    this.root = null;
  }
  insert(value){
    const newNode = new Node(value);
    if (this.root === null) {
      this.root = newNode;
    } else {
      let currentNode = this.root;
      while(true){
        if(value < currentNode.value){
          //Left
          if(!currentNode.left){
            currentNode.left = newNode;
            return this;
          }
          currentNode = currentNode.left;
        } else {
          //Right
          if(!currentNode.right){
            currentNode.right = newNode;
            return this;
          } 
          currentNode = currentNode.right;
        }
      }
    }
  }
  lookup(value){
    if (!this.root) {
      return false;
    }
    let currentNode = this.root;
    while(currentNode){
      if(value < currentNode.value){
        currentNode = currentNode.left;
      } else if(value > currentNode.value){
        currentNode = currentNode.right;
      } else if (currentNode.value === value) {
        return currentNode;
      }
    }
    return null
  }
  // remove 도 있지만 길어서 뺐다. 
}

AVL Tree, Red/Black Tree

이전 글에서 다루었던 Unbalanced Tree가 생기는 상황을 피하도록 값이 들어올때 값에 따른 level의 변화를 탐지하고 level이 같아지도록 부모노드를 조정하는 기능이 있는 tree이다.

직접 코드를 작성하는 일은 거의 없겠으나 존재 이유와 기능은 알아둬야한다.

여기서는 유용한 사이트 링크를 남겨두는 것으로 대체하겠다.(너무 복잡하다 ㅠㅠ )

AVL Tree

AVL Tree 시뮬레이션 사이트 : https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

AVL Tree 작동원리 글 포스트 :
https://medium.com/basecs/the-little-avl-tree-that-could-86a3cae410c7

Red/Black Tree

Red/Black Tree 시뮬레이션 사이트 : https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

Red/Black Tree 작동원리 글 포스트 :
https://medium.com/basecs/painting-nodes-black-with-red-black-trees-60eacb2be9a5

Binary Heap

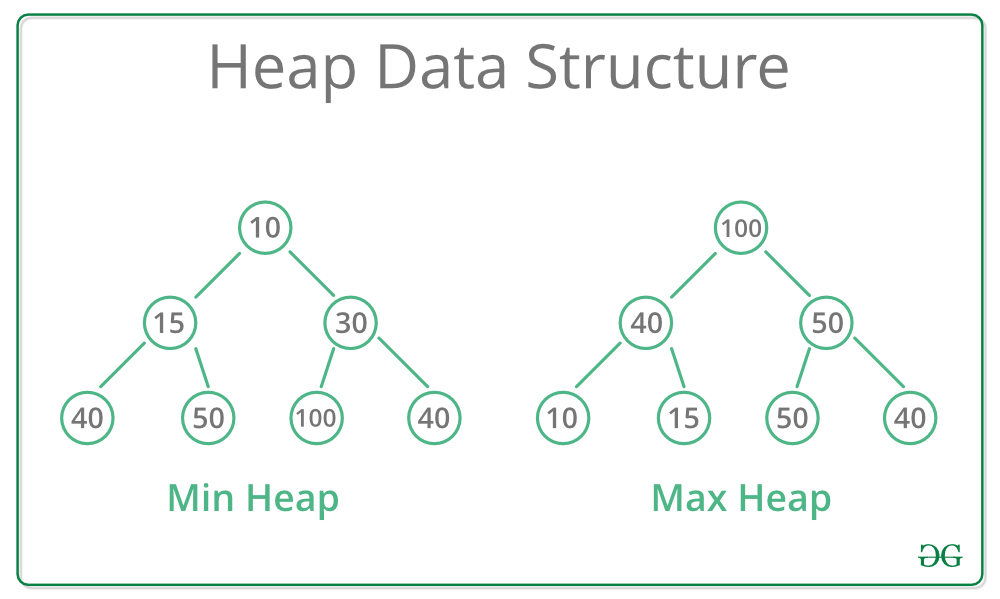
root에 제일 큰 값 또는 작은 값이 들어가고 밑으로 갈수록 작거나 큰 값을 가지는 tree구조의 heap이다.

Min Heap이 갈수록 커지는 값을 가지는 구조이고
Max Heap이 갈수록 작아지는 값을 가지는 구조이다.

같은 Level의 노드끼리는 부모보다 크다 또는 작다 라는 특징 말고는 관계가 없다.
그래서 lookup의 시간복잡도가 O(n)
insert 와 delete는 그대로 O(logN)

시뮬레이션 페이지 : https://visualgo.net/en/heap

사용이유

값들을 비교하기가 좋다. -> 예: Max Heap에서 33보다 큰 값을 얻고 싶다면 단순히 lookup을 한 후 33의 Level 이상의 노드만 보면 된다.

Memory Heap !== Heap Data Structure
JS엔진의 메모리 힙과는 다른 힙이다.

참고
Udemy " Master the Coding Interview: Data Structures + Algorithms " - Zero To Mastery