Optimization for Deep Learning
optimization은 decision science에서 중요한 툴로 사용된다.
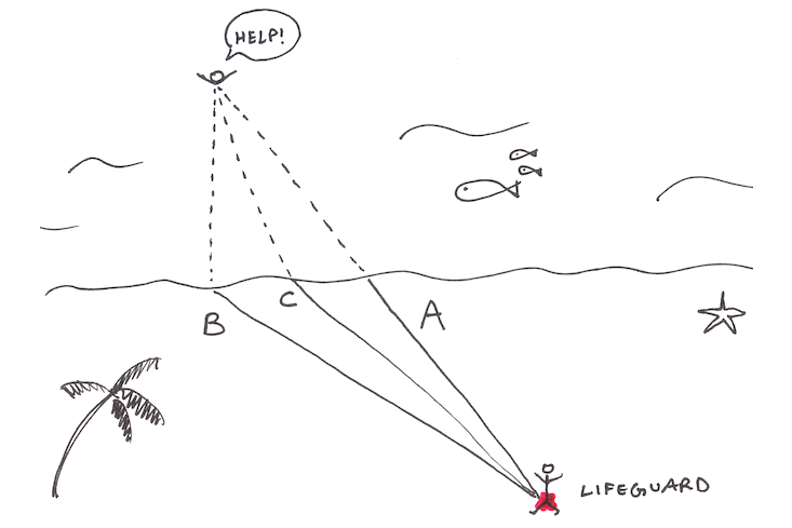
예를 들어, 라이프 가드와 바다에 빠진 사람이 존재한다.
이때 A, B, C 루트 중 하나를 선택하여 요 구조자를 구할 것인지 결정 해야하는 상황에서
시간 최소화, 거리 최소화, 요 구조자 생존률 최대화 등 최적화 도메인을 설정하여 최적의 변수 찾는 과정이다.
이때, 중간에 돌이 있다든지, 구멍이 있다든지 제약조건이 존재할 수도 있고, 이러한 제약 조건 하에 최적의 값을 찾아나간다.
Optimization에는 3가지 key components가 있다.
- Objective function(목적함수-eg.시간)
- Decision variable(eg. route A,B,C)
- constraints(제약 조건)
최적화의 절차
- 주어진 문제의 objective, variables, and constraints가 뭔지 identify하는 절차(모델링)
- Find its optimal solutions
mathematical expression
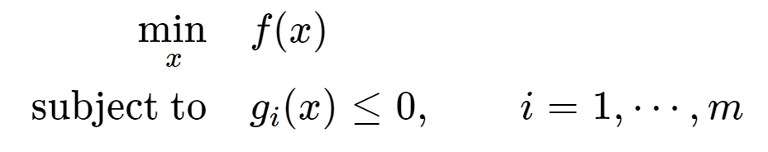
dicision variable x가 objective function f(x)로 표현되었다고 할때, 최소로 하는 x를 찾는 문제
constraint가 있을 수 있기 때문에 subject to g_i(x)로 나타낸다. g_i(x)=i번째 제약조건을 나타낸다.
constraints g_i(x)를 만족하는 x의 부분집합을 feasible region이라고 한다.
x의 값이 유한하지 않을 수 있기 때문에 일일히 evaluation 해보는 것은 불가능에 가깝다.
optimal하다?ˀ 이러한 feasible region 중에서 가장 최소로 하는 값(minimization 문제라면)
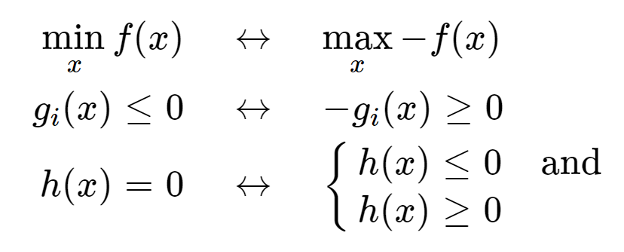
maxmization을 할경우 objective function에 마이너를 붙여 convert한다.
constraint g_i(x) 또한 동일하다.
등호인 constraint가 있을 경우 constraint를 위와 같이 표현할 수 있기때문에, minimal한 form은 상단의 것으로 약속한다.
Solving Optimization Problems
- Starting with the unconstrained, one dimensional case
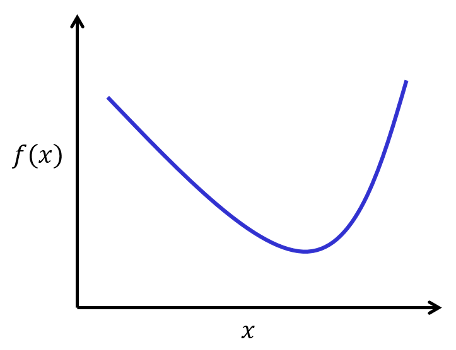
여기서 f’(x)=0 인 점에서 local minimum을 찾을 수 있다.
for convex(볼록함수) problems, guaranteed global minimum
decision variable이 n개 경우로 확장해보자
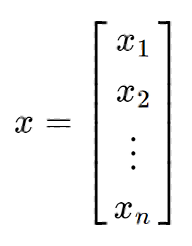
이경우 column vector로 위와 같이 표현한다.
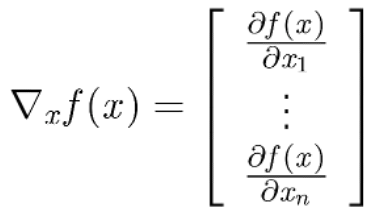
각각의 variable에 대해 편미분을 진행 했을 때(gradient),
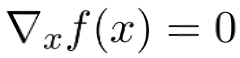
인 점이 optimal point가 된다.
예제를 풀어보자.
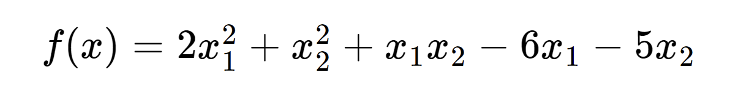
이 문제에서의 variable의 차원은 2이고, 각각의 variable에 대해 편미분을 진행하자.
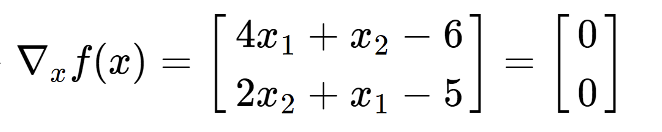
gradient가 0이 되는(0벡터가 되는) 값을 구하자.
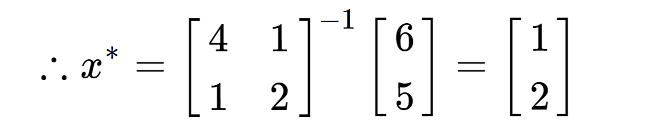
x는 위와 같은 결과가 나오고 이 값은 곧 optimal point x(x*)가 된다.
위와 같이 direct한 방법 말고도, iterative한 방법으로도 solution을 찾을 수 있다.
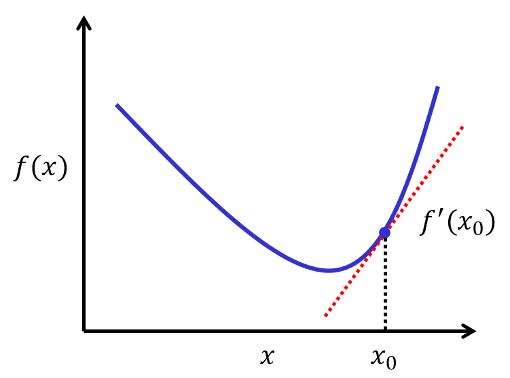
idea?
미분을 했을때 기하학적인 의미를 살펴보면 f’(x)은 가장 가파른 방향으로의 direction을 나타낸다.
그러면 minimization 문제에서 우리는 f’(x)을 찾기 때문에 랜덤한 x값에서 시작하여 direction의 반대방향으로 업데이트해나가게 된다.
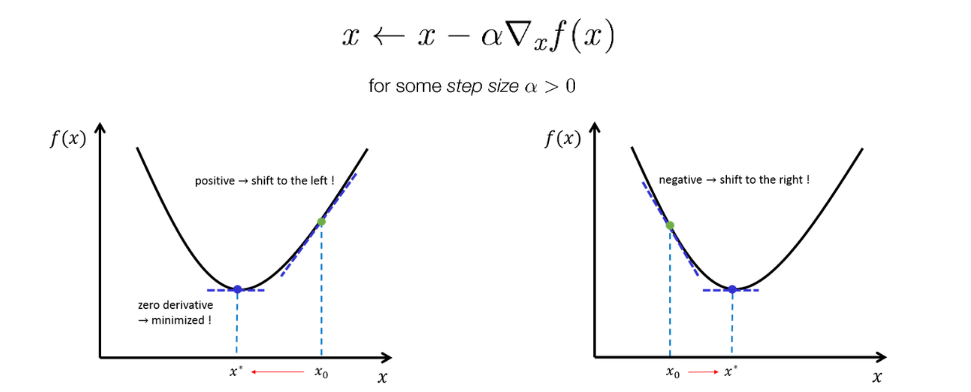
이렇게 반복적으로 업데이트하며 optimal한 point를 찾아가게 되는데, 이 방법을 gradient descent 방법이라고 한다. 이 방법의 경우 최소한 local minimum solution으로 수렴함을 보장한다.
함수가 매우 복잡할 경우, closed form의 함수가 존재하지 않는 등 다양한 이유로 해석적 direct method로 풀 수 없을때, 컴퓨터를 이용하여 iterative한 방법으로 풀 수 있기에 optimization에서 iterative method가 중요시 사용된다.
고차원에서도 gradient descent 방법을 적용한다면, optimal solution에 접근한다는 것을 기하학적인 형상을 통해 직관할 수 있다.
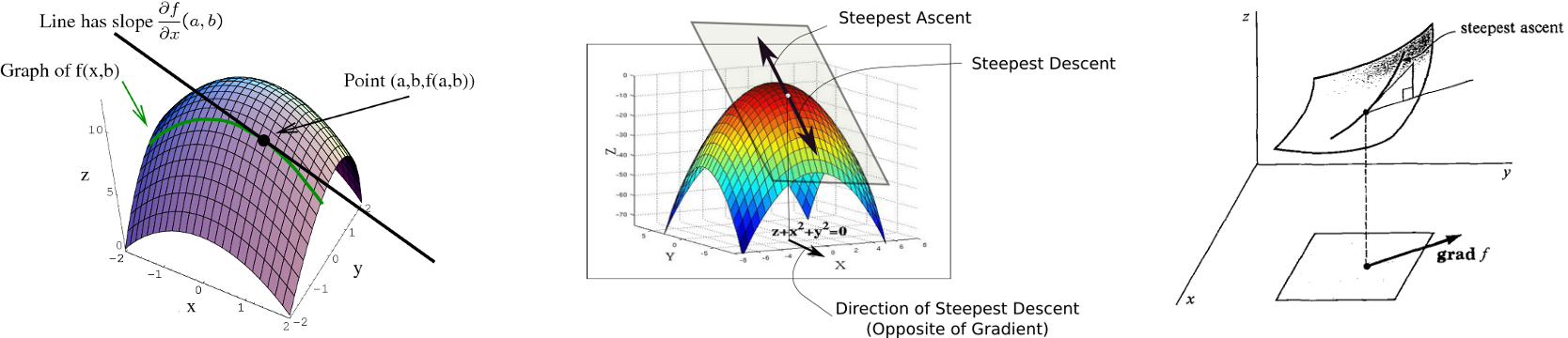
기하학적인 형상.
실제로 파이썬으로 적용해보자.
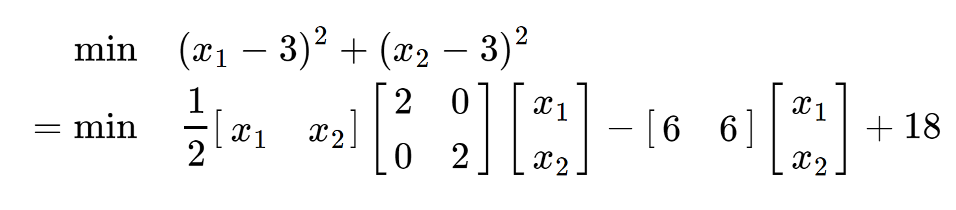
위 식은 직접적인 방법으로 풀면 x*=[[3],[3]]임을 알 수 있다. 아래와 같이 변환하여 gradient descent method를 적용해보자.

실제 파이썬 실습을 통해 실제 3에 근사함을 알 수 있다.
그러면 여기서 alpha값은 어떤 의미를 가지는가?
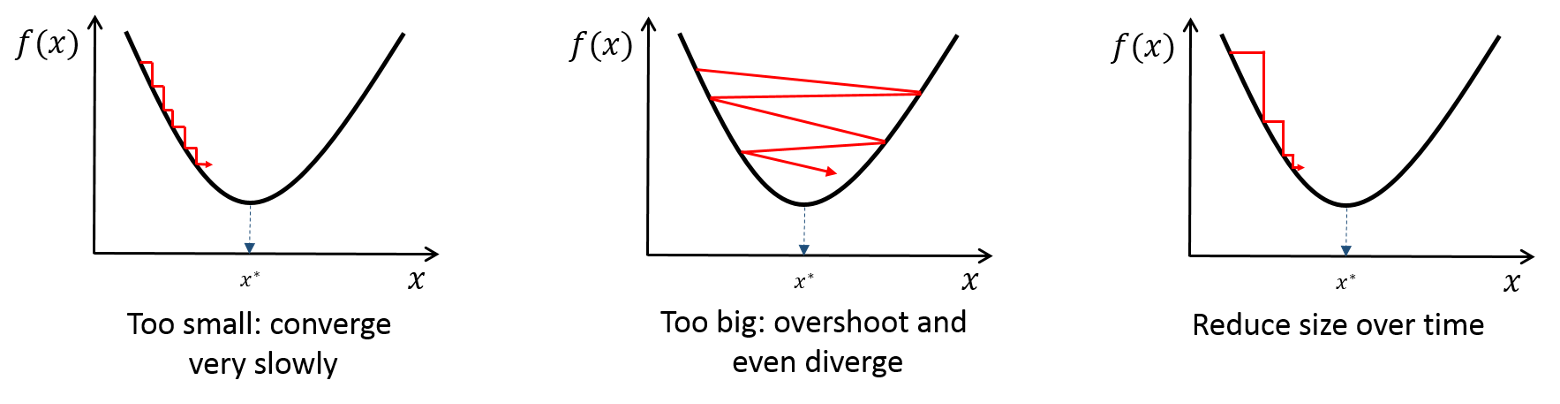
alpha 값이 작을경우 많은 iteration을 해야하므로 많은 시간이 걸리게 된다.
alpha 값이 클 경우 overshoot이 발생한다.
그러면 gradient descent method는 항상 수렴성을 보장하는가?
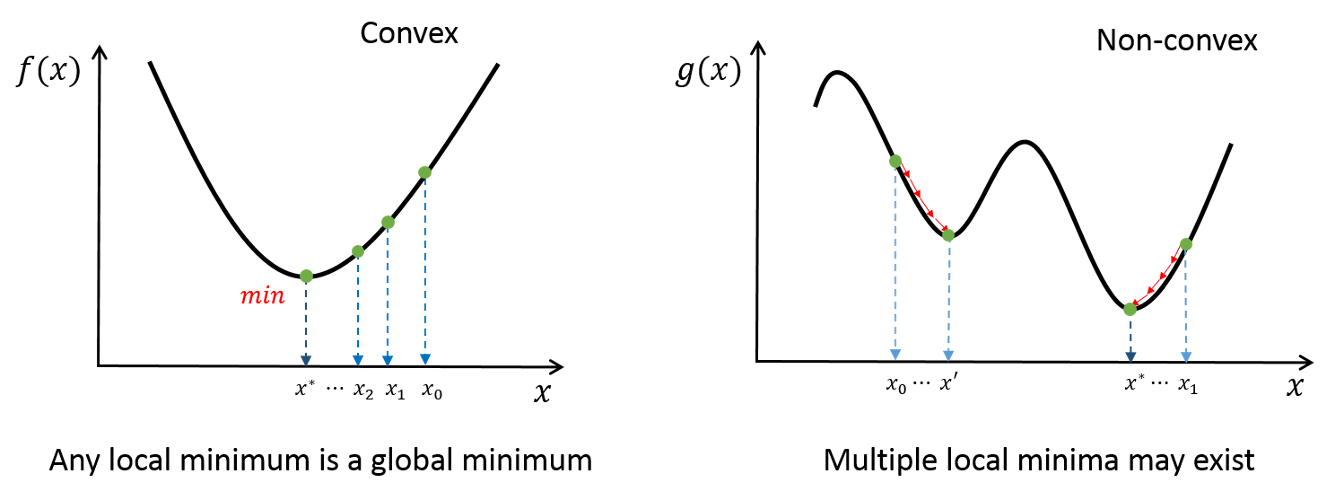
multiple local minimum이 존재할 경우, global minimum으로의 수렴을 보장하지 않는다.
그러면 어떻게 수행을 하는가?ˀ → radom으로 여러번에 걸쳐 시행하는 방법이 practical하게 사용된다. 물론 optimal(global minimum) solution을 보장하지는 않는다.
Gradient Descent방법은 매우 general 하고 generic 하기 때문에, neural networks나 deep learning에서 활용된다. TensorFlow에는 기본적으로 Gradient Descent 방법이 임베디드 되어 있어 손실 함수를 정의하고 decision variable 값을 찾을 때 사용된다.
복습
- 최적화(optimization):
최적화는 주어진 제약 조건(constraints) 하에서 목적 함수(objective function)를 최대화 또는 최소화하는 결정 변수(decision variable)의 값을 찾는 과정을 의미한다. 이는 다양한 분야에서 중요한 툴로 사용되며, 문제의 형태에 따라 시간 최소화, 거리 최소화, 요구조자 생존률 최대화 등과 같이 다양한 목적을 달성할 수 있다. - 최적화의 절차:
- Modeling: 주어진 최적화 문제를 수학적으로 표현하기 위해 objective function, decision variable, constraints 등을 정의하는 단계이다. 목적 함수와 제약 조건을 정확히 나타내어야 하며, 문제를 이해하고 수학적으로 표현하는 과정이 중요하다.
- Find its optimal solutions: 최적화 문제에서는 가능한 모든 결정 변수의 조합을 확인하는 것이 불가능하므로, 최적의 결정 변수 값을 찾기 위해 Optimal solution을 탐색하는 알고리즘을 사용한다. 이러한 알고리즘은 주어진 제약 조건을 만족하면서 목적 함수를 최대화 또는 최소화하는 결정 변수 값을 찾아내도록 도와준다.
- Feasible Region :
제약 조건을 만족하는 결정 변수들의 집합을 feasible region이라고 합니다. 이는 가능한 해의 공간을 제한하는 영역으로, 목적 함수를 최대화 또는 최소화하는데 있어서 가능한 variable들이 위치하는 영역을 의미한다. - Minimization과 Maximization:
목적 함수를 최소화하는 문제를 Minimization 문제라고 한다. 반대로, 목적 함수를 최대화하는 문제는 Maximization 문제이다. Maximization 문제는 Objective function에 마이너스를 붙여서 Minimization 문제로 convert하여 표현할 수 있다.
- direct method to solve problem
- Unconstrained, One-Dimensional Case:
처음에 설명한 1차원의 무제약(unconstrained) 최적화 문제에서, 목적 함수 f(x)의 미분값이 0인 지점에서 local minimum을 찾는다. 이러한 점에서는 local minimum이 보장되며, 또한 함수가 볼록 함수(convex function)인 경우에는 global minimum도 이러한 지점에서 찾을 수 있다. - Multi-Dimensional Case:
결정 변수가 여러 개인 n차원의 경우, 최적화 문제를 해결하기 위해 gradient와 편미분을 사용한다. Gradient는 함수의 가장 가파른 방향을 나타내고, 편미분을 사용하여 각 변수에 대한 변화율을 계산한다. 이때, 최적의 결정 변수 값은 gradient가 0인 지점이 되는데, 이를 optimal point라고 한다.
- itractive method to solve problem
- Gradient Descent:
경사 하강법(Gradient Descent)은 함수의 기울기(gradient) 방향의 반대로 iterative하게 업데이트하는 방법으로, 최적화 문제를 풀기 위해 많이 사용되는 방법 중 하나이다. 이 방법은 초기에 임의의 시작점에서 시작하여 gradient의 반대 방향으로 이동하면서 최적점을 찾아가게 된다. 경사 하강법은 반복적인 업데이트를 통해 점점 최적점으로 수렴하며, 함수가 복잡하거나 해석적으로 solution를 구하기 어려울 때 유용하게 사용되기 때문에, optimization에서 중요하다. - Gradient Descent의 수렴성:
Gradient Descent는 목적 함수가 convex fuction인 경우에는 global minimum으로 수렴하는 것을 보장한다. 하지만 목적 함수가 비볼록 함수이고 다수의 local minimum이 존재할 경우, Gradient Descent는 global minimum으로 수렴을 보장하지 않는다. 이러한 문제를 피하기 위해 다양한 초기화를 시도하거나, 학습률을 조정하는 등의 방법으로 여러 번 시행하여 근사적인 optimal solution을 찾는 것이 일반적이다.
