출처는 여기

Background

하이퍼 파라미터 vs 모델 파라미터

모델 파라미터

Network Weight Paramter 라고도 불리는 모델 파라미터는 모델이 데이터를 학습하면서 자동으로 결정되는 값이다. 이 값들은 신경망의 가중치 같은 내부 설정값을 포함한다. 이러한 파라미터들은 모델이 학습하는 과정에서 조정되며, 이는 모델이 주어진 데이터를 가장 잘 예측하도록 돕는다.

하이퍼 파라미터

하이퍼파라미터는 모델을 생성하거나 학습을 시작하기 전에 사용자가 직접 설정해야 하는 값이다. 학습률(learning rate)이나 배치 크기(batch size)와 같은 값들이 여기에 속한다. 이러한 값들은 모델의 학습 과정과 성능에 큰 영향을 미친다.

하이퍼파라미터와 모델 파라미터의 차이

하이퍼파라미터와 모델 파라미터의 주요 차이점은, 모델 파라미터는 모델이 데이터를 학습하면서 자동으로 결정되는 반면, 하이퍼파라미터는 사용자가 모델을 생성하거나 학습을 시작하기 전에 직접 설정해야 한다는 점이다.

하이퍼파라미터 튜닝이란?

하이퍼파라미터 튜닝은 사용자가 설정하는 하이퍼파라미터의 최적값을 찾는 과정을 말한다. 즉, 어떤 하이퍼파라미터 값이 모델 성능을 최대화하는지를 찾는 작업이다.

하이퍼파라미터 튜닝을 위해서는 다양한 실험을 진행하고, 그 결과를 기반으로 하이퍼파라미터 값을 조정해야 한다. 이 과정은 간단한 모델에서 시작하여 점진적으로 모델을 개선하는 방식으로 진행되며, 이를 돕기 위한 다양한 도구와 프레임워크(예: MLFlow, WanDB 등)도 있다.

Optimizer

• 딥러닝의 학습은 기본적으로 손실값(loss value)이 가장 작은 모델을 찾는 과정이다. 이는 데이터로부터 학습하여 예측 오차를 최소화하는 모델 파라미터를 찾는 것을 의미한다.

• 학습은 손실함수(loss function)의 최소값을 찾아가는 과정이며, 이 과정을 최적화(optimization)라고 한다. 최적화를 수행하는 알고리즘을 옵티마이저(optimizer)라고 부른다.

Abstract

• "An overview of gradient descent optimization algorithms"는 경사 하강법 최적화 알고리즘의 다양한 변형에 대해 설명하는 논문이다.
• 이 논문은 이러한 알고리즘들의 동작 원리와 장단점에 대한 직관적 이해를 제공하고, 병렬 및 분산 환경에서의 최적화 전략과 아키텍처에 대해 설명한다.
• 이를 통해 기존에 블랙박스처럼 사용하던 최적화 알고리즘을 이해하고, 더 효과적으로 사용하는 방법을 이해할 수 있다.

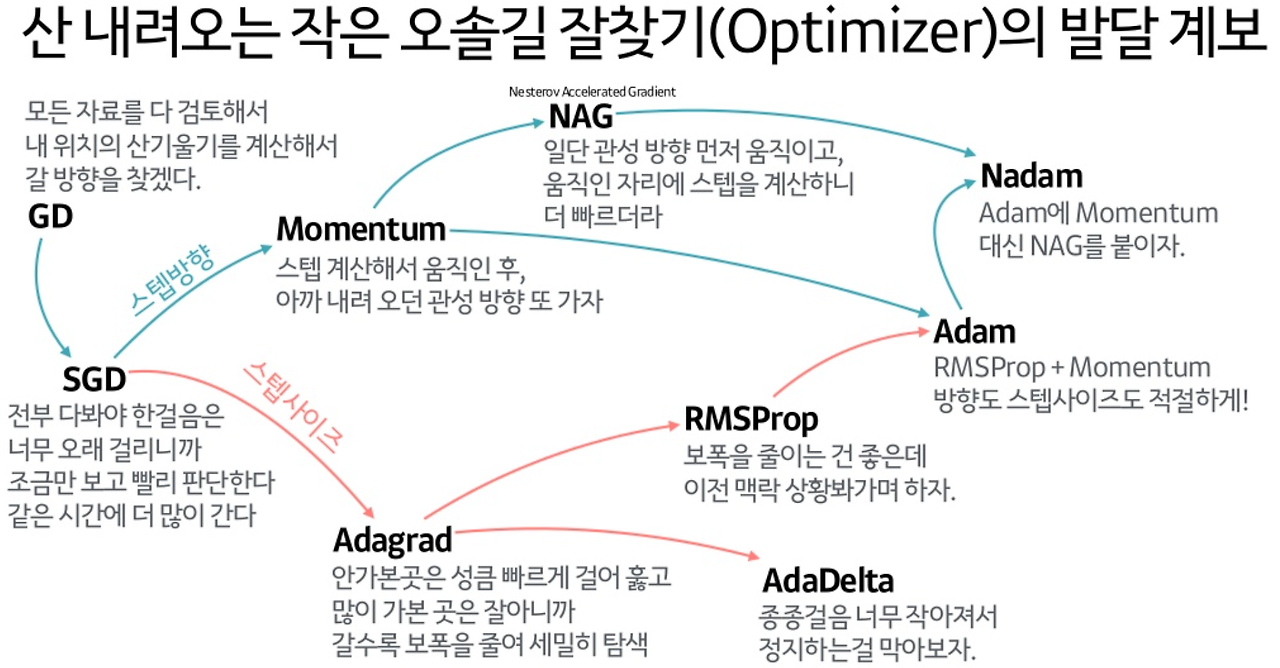
Optimizers

01.Vanilla gradient descent(batch gradient descent) (1847)

경사 하강법은 최적화 알고리즘의 기본적인 형태로, 비용 함수의 기울기(경사)를 사용하여 최솟값을 찾는다. 각 단계에서 현재 위치의 기울기를 계산하고, 그 기울기가 가리키는 "하강" 방향으로 이동한다. 이 방법은 1847년에 Cauchy에 의해 소개되었다.

수식

$\theta = \theta - \eta \cdot \nabla_{\theta} J(\theta)$

• $\theta$: 파라미터 또는 가중치. 이 값들은 우리가 최적화하려는 대상
• $\eta$: 학습률(learning rate). 이 값은 경사 하강법의 각 단계에서 얼마나 멀리 이동할지를 결정한다. 학습률이 너무 크면 최적의 솔루션을 넘어서 버릴 수 있고, 너무 작으면 수렴하는 데 너무 오래 걸릴 수 있다.
• $\nabla_\theta J(\theta)$: 비용 함수 $J(\theta)$의 $\theta$에 대한 그래디언트(경사). 이 값은 비용 함수가 감소하는 방향을 나타낸다.

02.Stochastic Gradient Descent (SGD, 1951)

전체 데이터 세트를 사용하는 대신, SGD는 각 단계에서 하나의 훈련 예제를 무작위로 선택하여 그라디언트를 계산한다. 이 방법은 더 빠르지만, 더 많은 노이즈가 있어 최적값에 수렴하는 것이 불안정할 수 있다. 이 방법은 1951년에 Robbins와 Monro에 의해 소개되었다.

수식

$\theta = \theta - \eta \cdot \nabla_{\theta} J(\theta; x^{(i)}; y^{(i)})$

• $x^{(i)}$와 $y^{(i)}$는 각각 i번째 훈련 샘플의 입력과 출력을 나타낸다.

03.Mini-batch gradient descent

미니배치 경사 하강법(Mini-batch Gradient Descent)에서 사용되는 업데이트 규칙이다. 미니배치 경사 하강법은 전체 데이터 세트를 사용하는 배치 경사 하강법과 한 번에 하나의 샘플만을 사용하는 확률적 경사 하강법(SGD) 사이의 절충안이다. 이 방법은 미니배치라고 하는 작은 샘플 집합을 사용하여 파라미터를 업데이트한다. 이 방법은 SGD보다는 덜 노이즈가 있고, 전체 배치보다는 계산 비용이 적기 때문에 실제로 많이 사용된다.

수식

$\theta = \theta - \eta \cdot \nabla_{\theta} J(\theta; x^{(i:i+n)}; y^{(i:i+n)})$

• $x^{(i:i+n)}$와 $y^{(i:i+n)}$는 각각 훈련 샘플의 입력과 출력을 나타내는데, 이는 $i$번째 샘플부터 $(i+n)$번째 샘플까지의 범위를 포함

Challenges :Disadvantages of GDs

하지만 경사하강법에는 아래와 같은 몇가지 단점이 있다.

학습률 선택

적절한 학습률(learning rate)을 선택하는 것은 어려울 수 있다. 학습률이 너무 작으면 수렴이 지나치게 느려질 수 있고, 학습률이 너무 크면 수렴이 방해받을 수 있으며, 손실 함수가 최소값 주변에서 진동하거나 심지어 발산할 수 있다.

학습률 일정

learning rate schedules가 고정되어있기 때문에, 학습률이 너무 크면 최소값을 넘어설 수 있고, 너무 작으면 수렴하는 데 너무 오래 걸리거나 지역 최소값에 갇힐 수 있다는 문제가 있다.

고차원 non-convex 함수 최소화의 어려움

아래 설명할 그림과 같이, $X^2sin(x)$와 같은 고차원 함수의 경우 최적을 찾기 어려운 단점이 있다.

04.Momentum (1964)

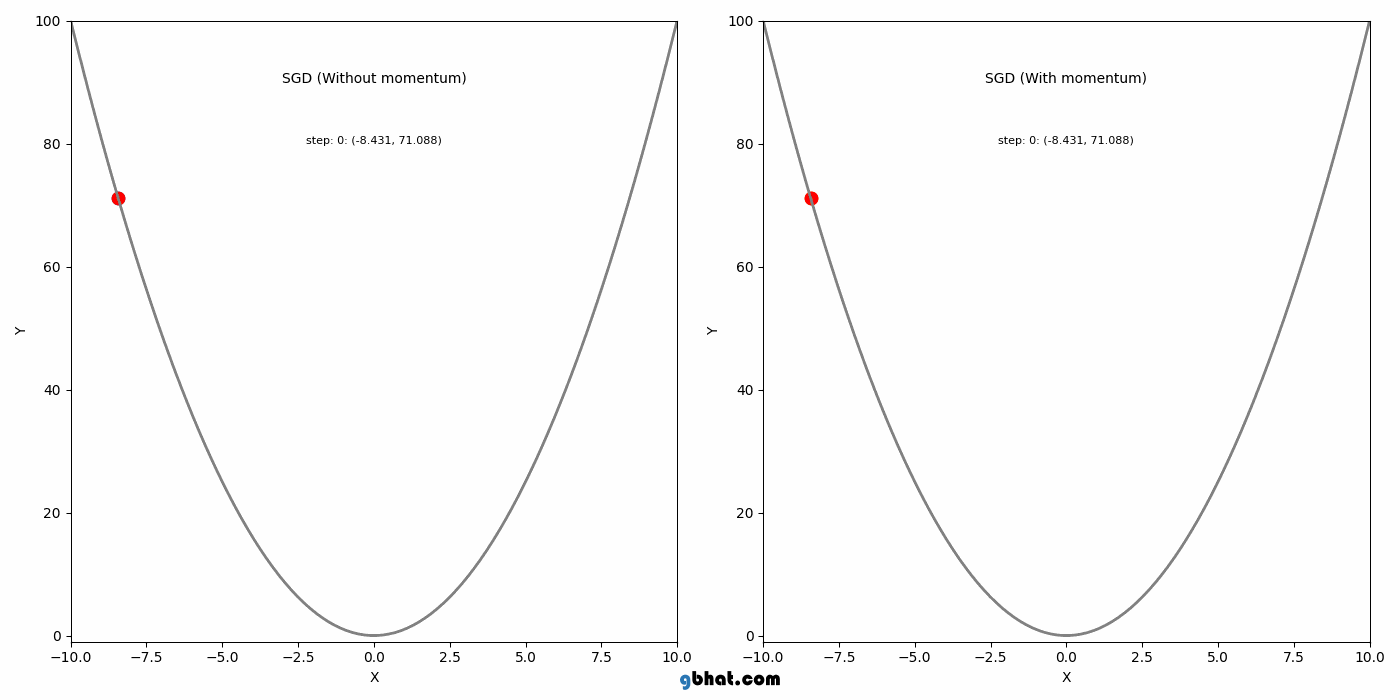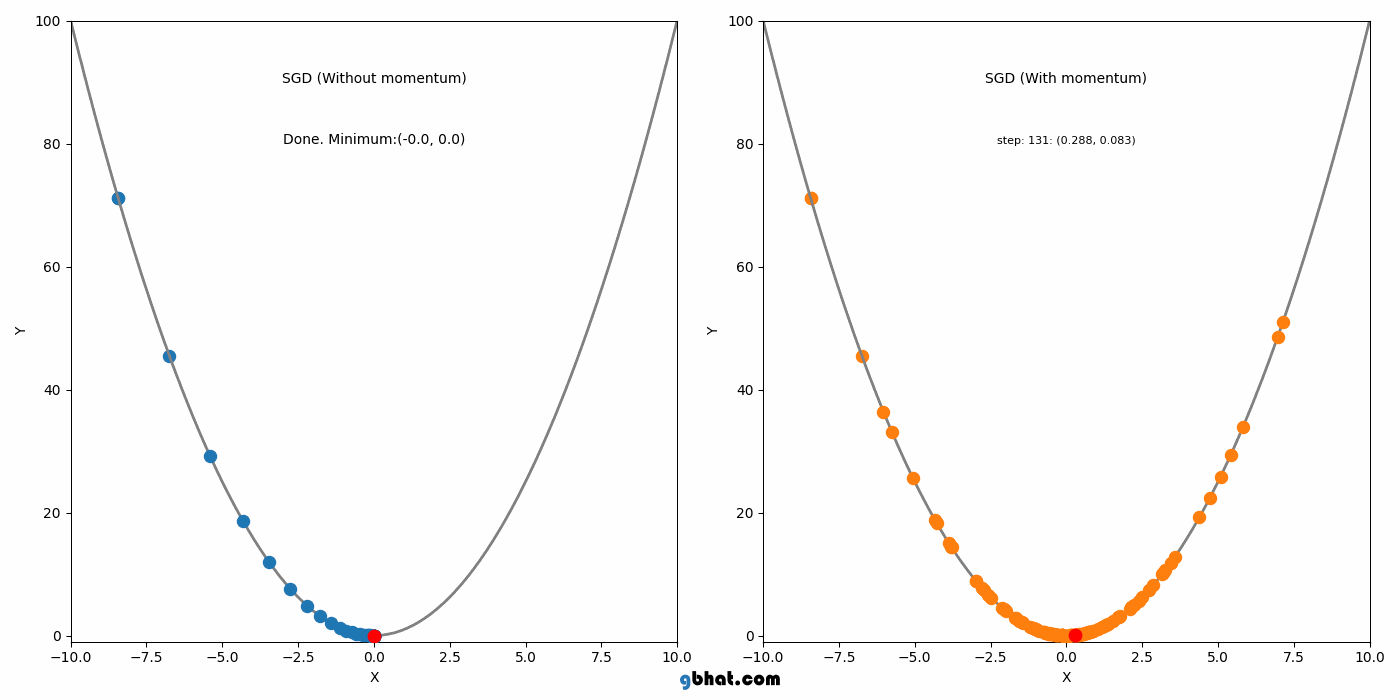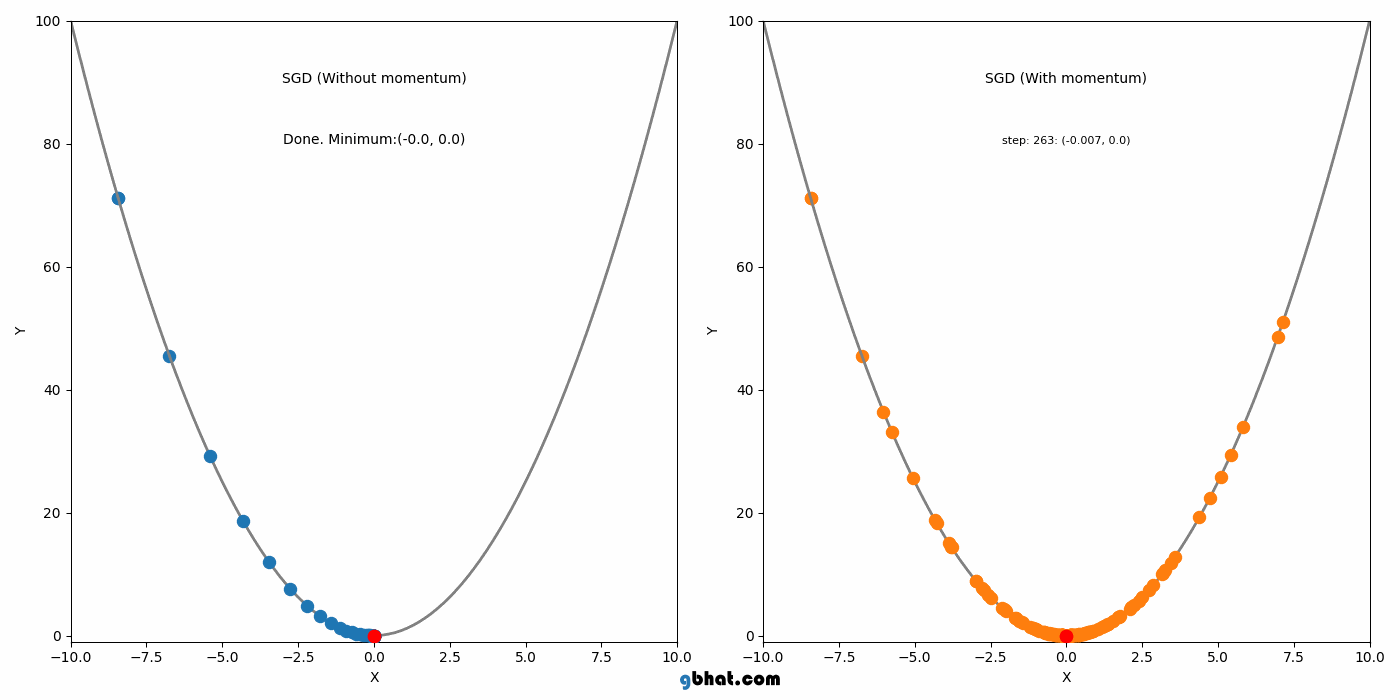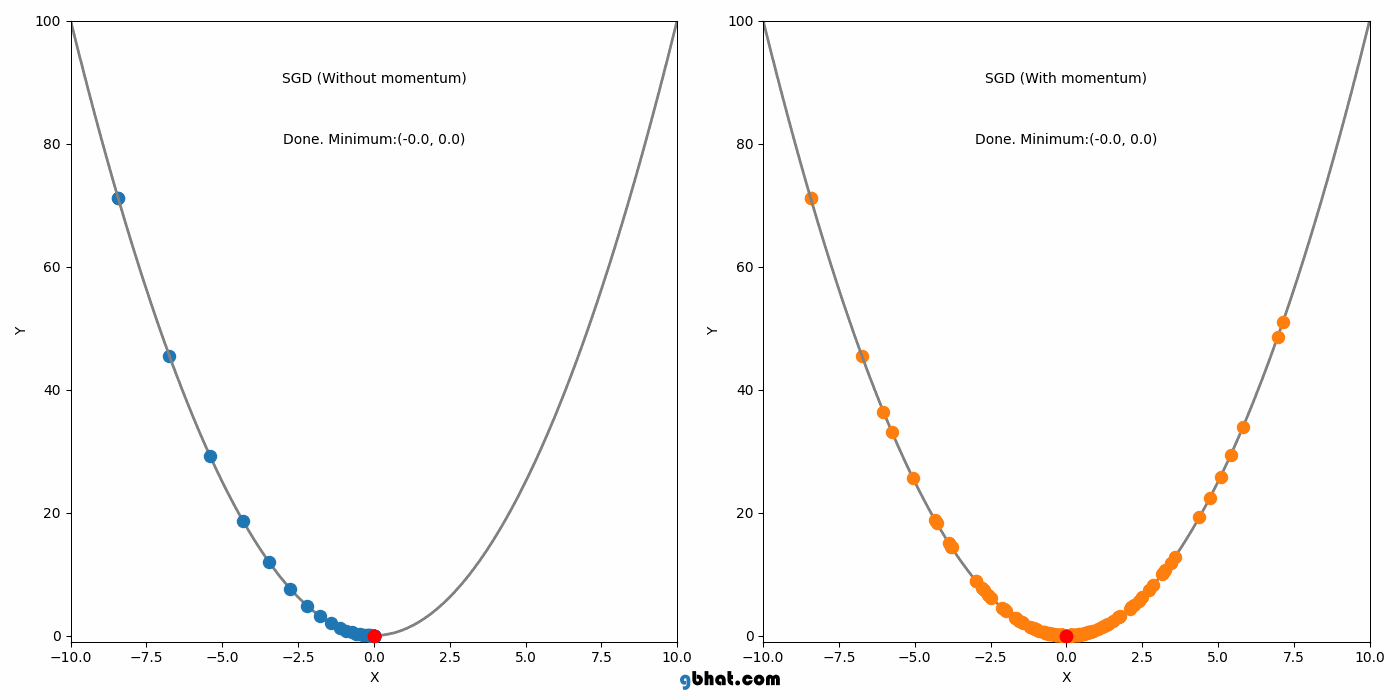
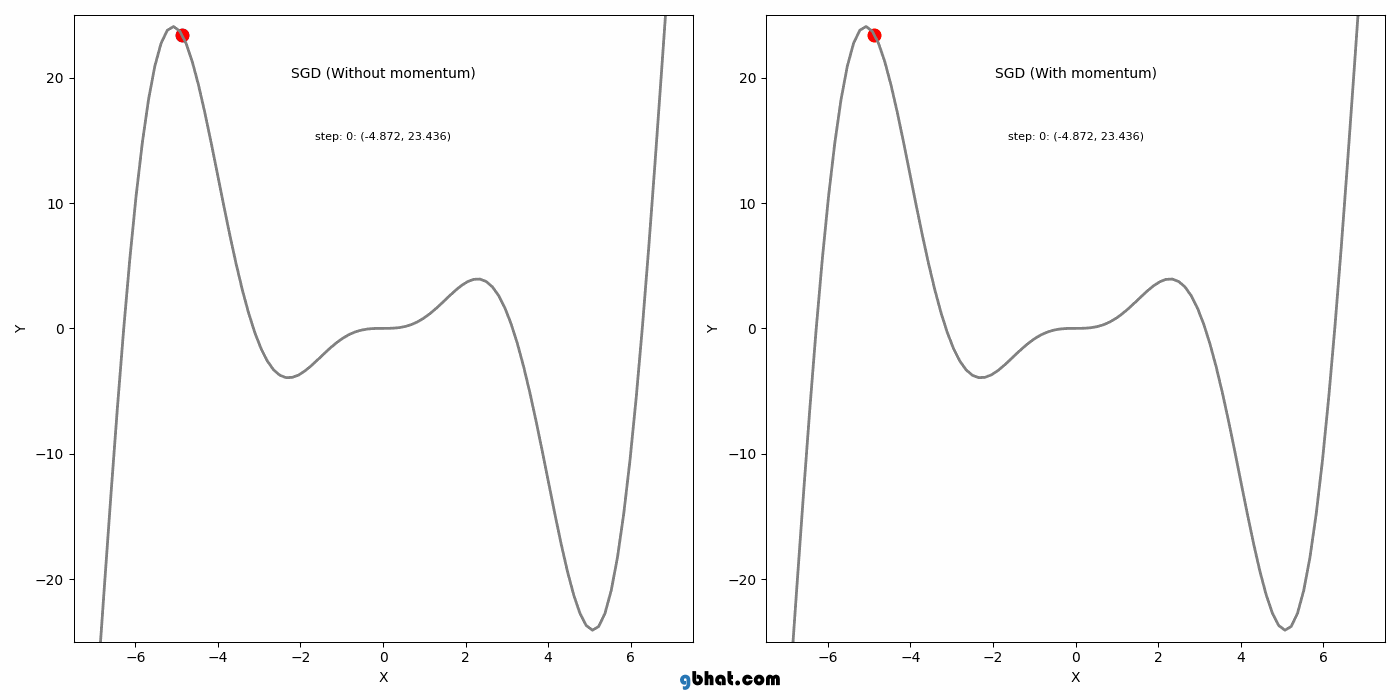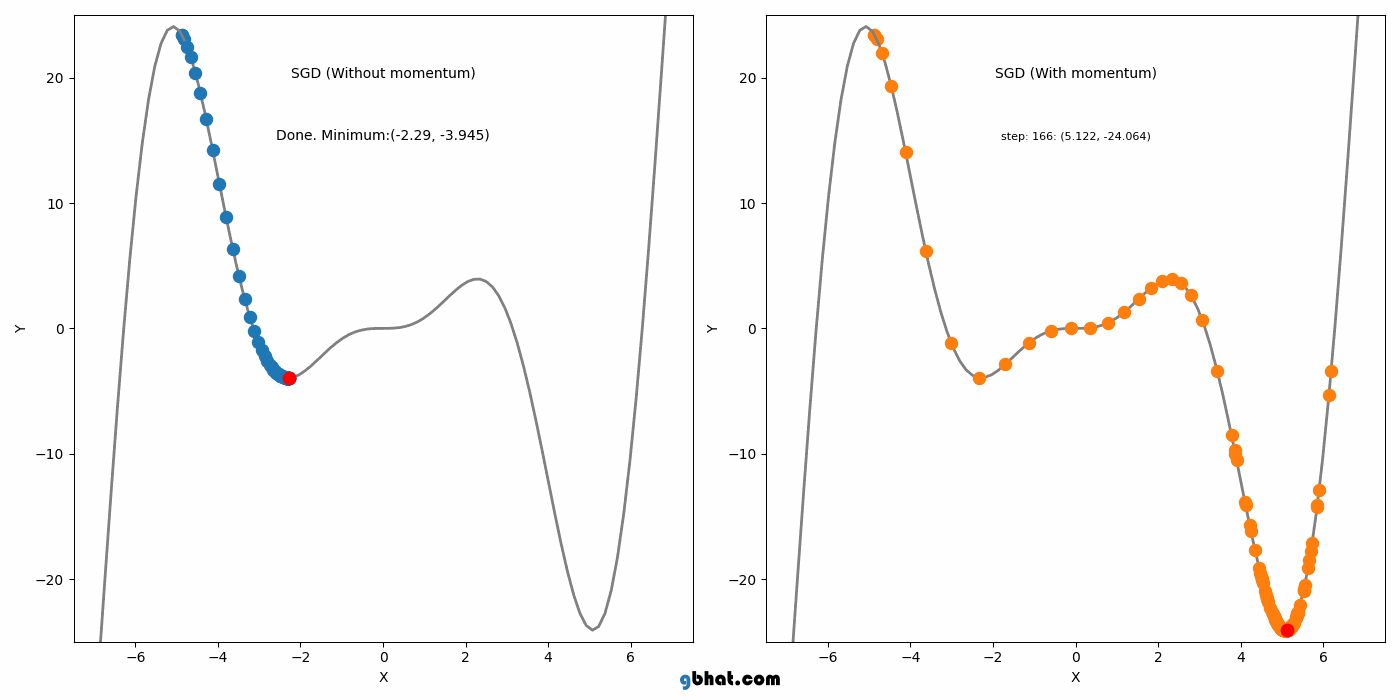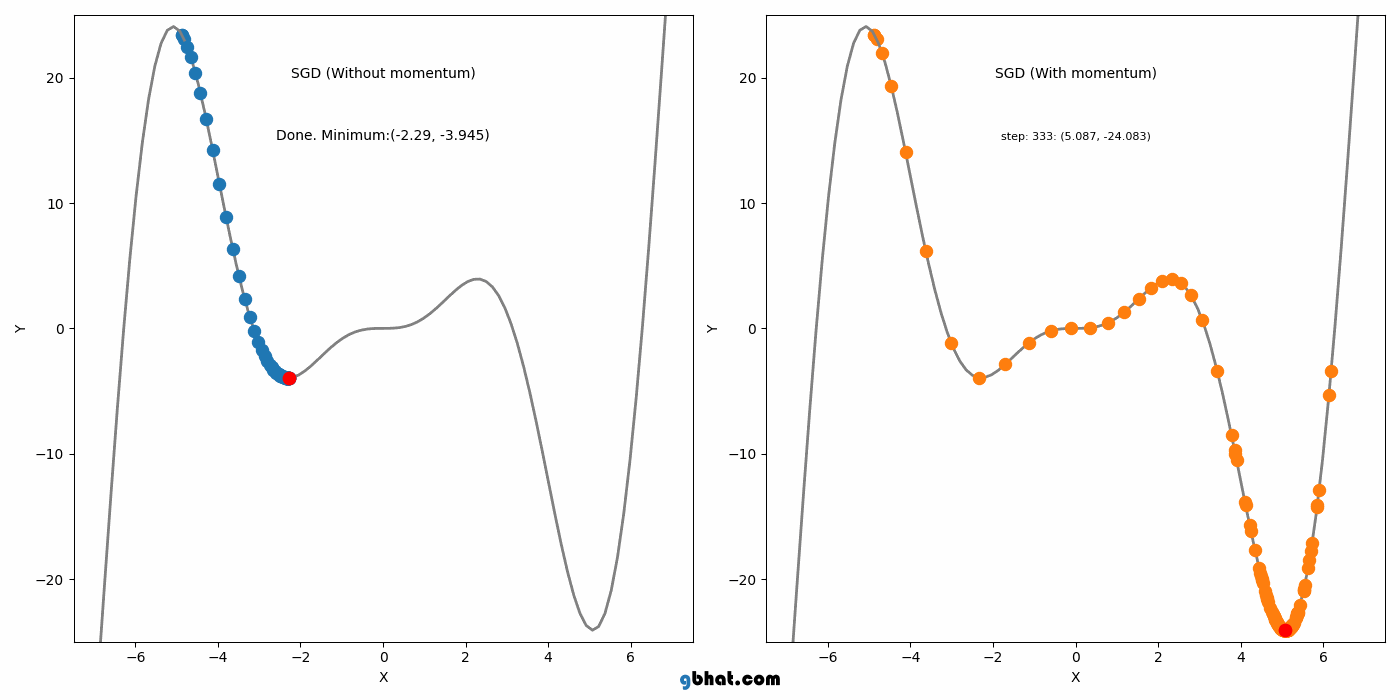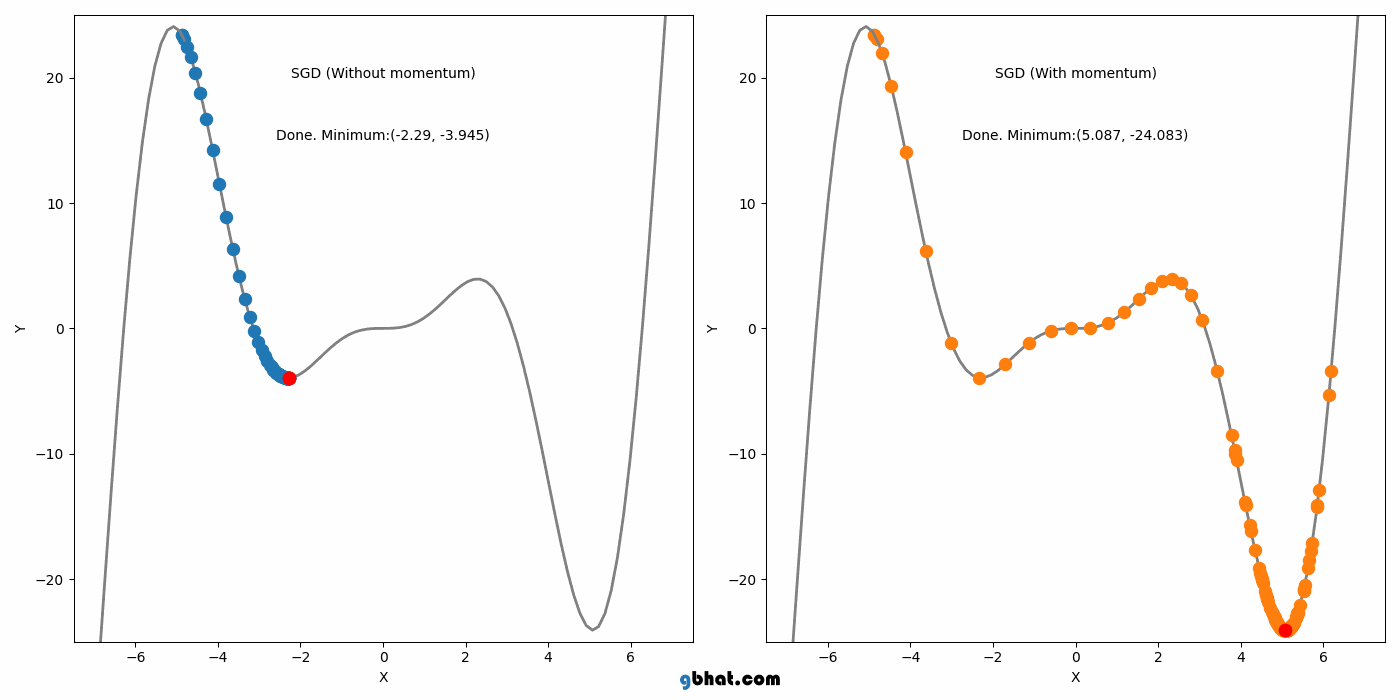
모멘텀은 SGD에 가속도를 추가하여 그라디언트가 일관된 방향으로 움직이는 것을 돕는다. 이 방법은 SGD의 주요 단점 중 local minimum을 벗어나지 못하는 점을 해결했다.

수식

$v_t = \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta)$
$\theta = \theta - v_t$

• $v_t$는 시간 $t$에서의 속도(velocity)로 이전 그래디언트의 가중치 합
• $\gamma$는 모멘텀 계수(momentum coefficient)로, 이전 그래디언트가 현재 그래디언트에 미치는 영향을 조절(일반적으로 0.9 정도의 값을 사용)
• $\eta$는 학습률(learning rate)
• $\nabla_{\theta} J(\theta)$는 비용 함수 $J(\theta)$의 그래디언트
• $\theta$는 업데이트할 매개변수

첫 번째 식은 속도 $v_t$를 업데이트하는 공식으로, 이전 속도와 현재 그래디언트에 대한 가중 평균이다. 두 번째 식은 가중치를 업데이트하는 공식으로, 현재 가중치에서 속도를 빼는 것으로 계산됩니다. 이렇게 하면, 가중치는 그래디언트의 방향으로 이동하는 동시에, 이전의 그래디언트도 고려하게 된다.

하지만 Momentum도 단점이 있는데, Momentum의 단점은 global minimum에서도 이 관성이 작용한다는 점이다. 그래서 global minimum도 벗어날 가능성을 가진다.

05.Nesterov Accelerated Gradient (NAG, 1983)

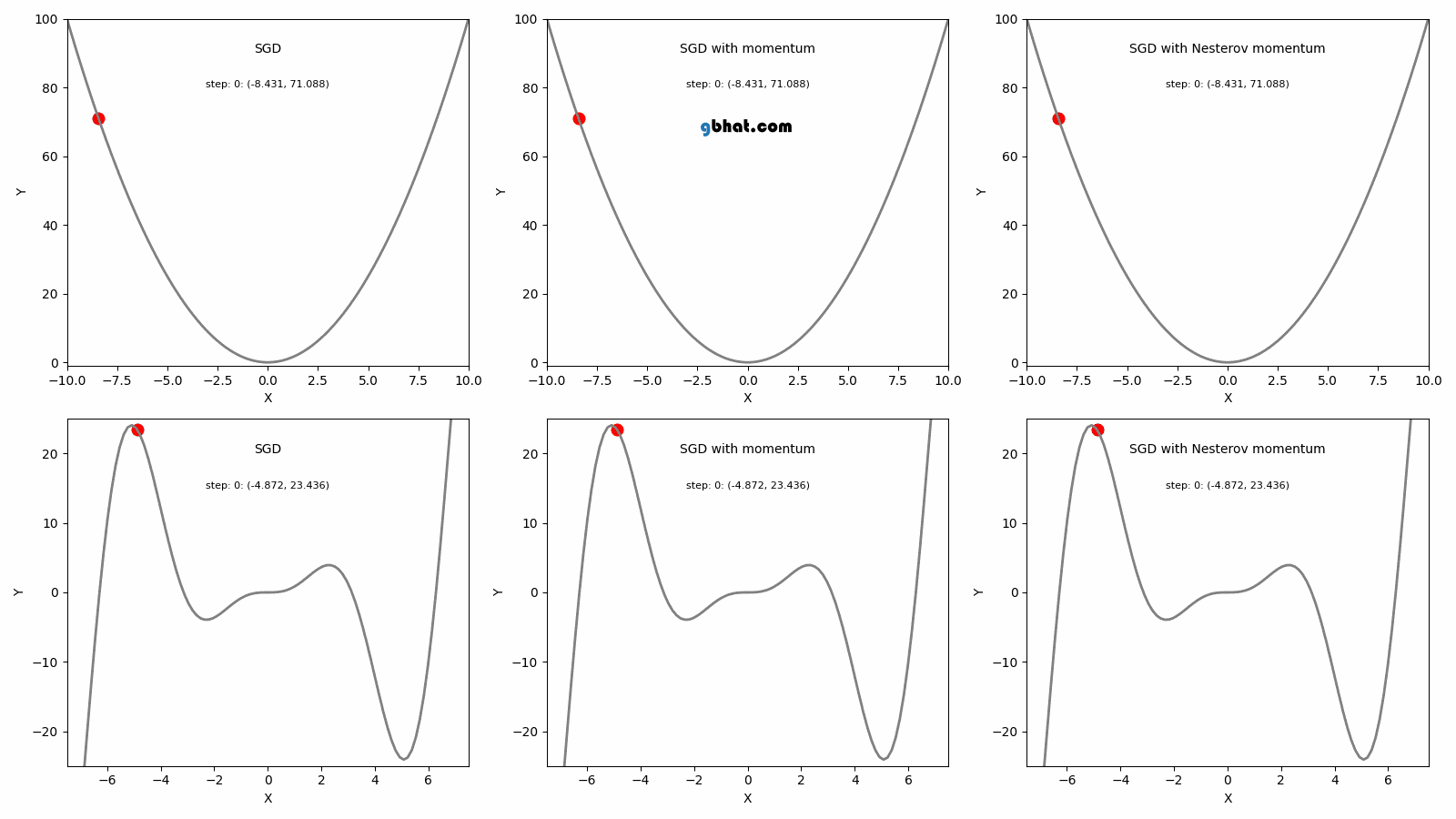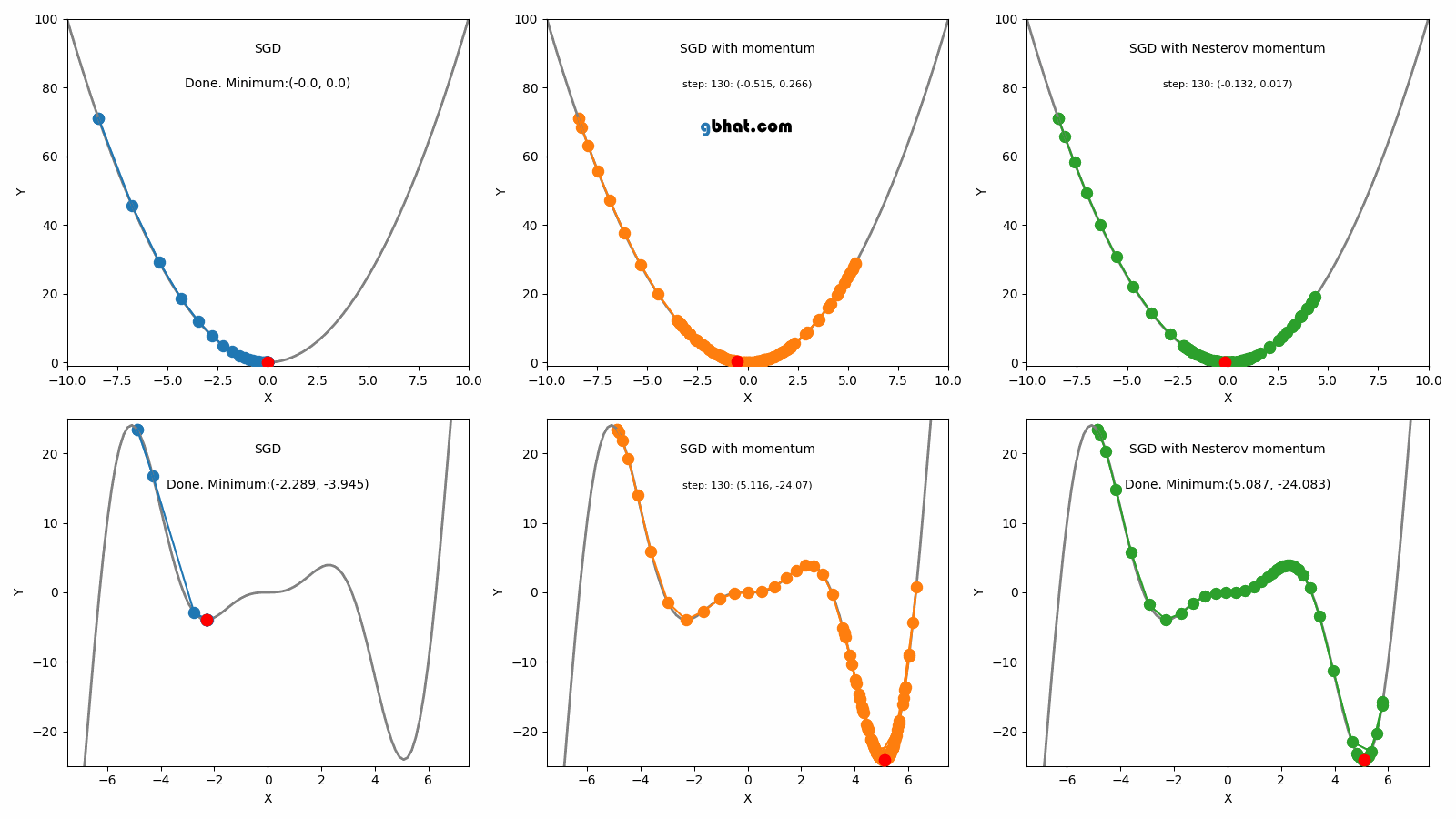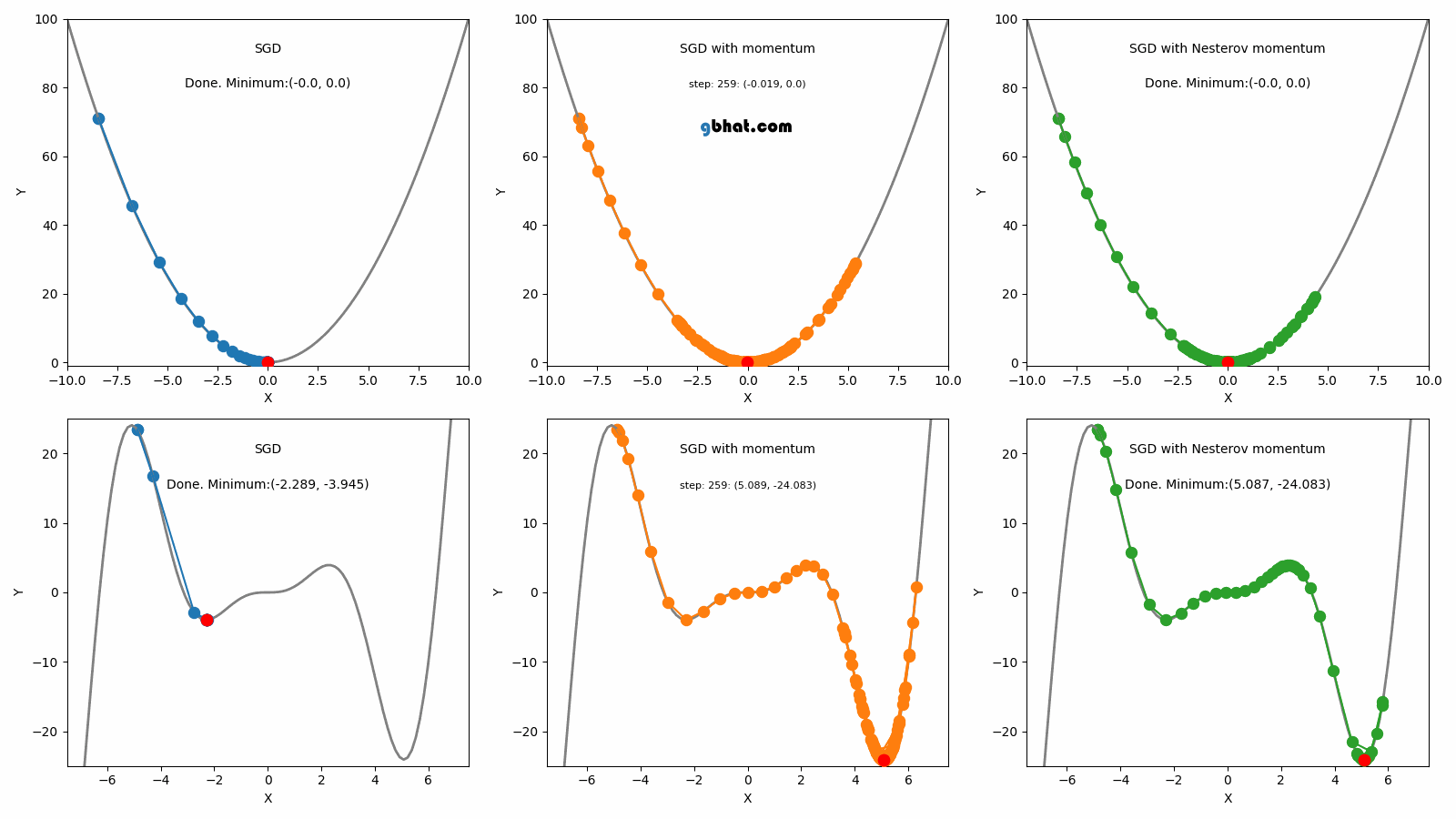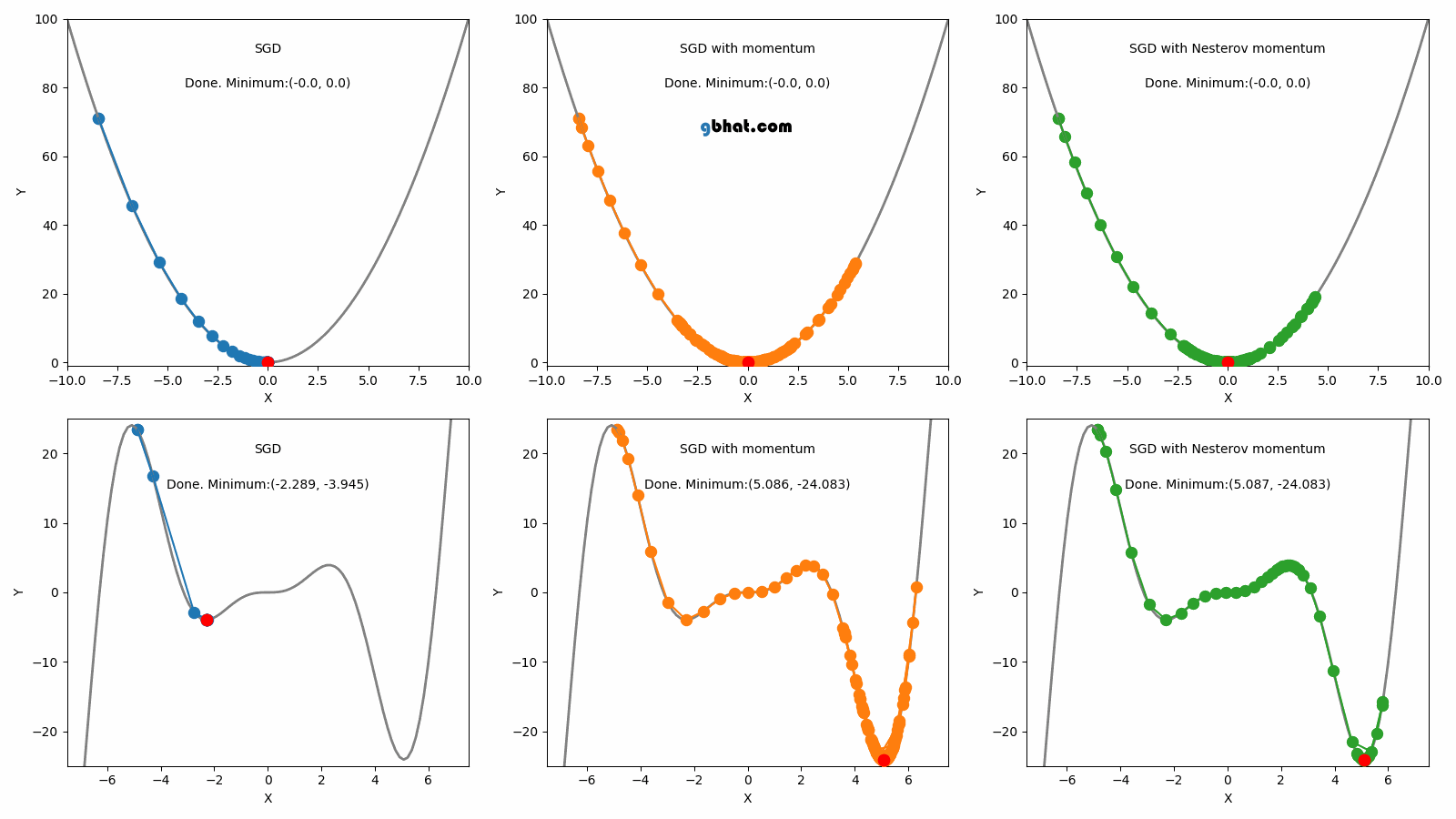
NAG는 모멘텀 방법을 개선한 것으로, 그라디언트를 계산할 위치를 더 정확하게 예측하여 보다 빠른 수렴을 가능하게 한다. 이 방법은 1983년에 Nesterov에 의해 소개되었다.

Nesterov Accelerated Gradient, NAG; 네스테로프 가속 경사법)은 모멘텀 방식의 한계를 극복하기 위해 제안된 방법이다. 모멘텀 방식은 수렴 지점에 도달해야 할 때도 모멘텀에 의해 해당 지점을 지나치는 문제가 있다. NAG는 이 문제를 해결하기 위해 모멘텀을 계산할 때, 모멘텀에 의해 발생하는 변화를 미리 고려하도록 설계되었다.

수식

$v_t = \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta - \gamma v_{t-1})$
$\theta = \theta - v_t$

• $v_t$는 시간 $t$에서의 속도(velocity)로 이전 그래디언트의 가중치 합
• $\gamma$는 모멘텀 계수(momentum coefficient)
• $\eta$는 학습률(learning rate)
• $\nabla_{\theta} J(\theta - \gamma v_{t-1})$는 비용 함수 $J$의 그래디언트를, 이전 단계의 모멘텀으로 조정된 매개변수 위치에서 계산한 것
• $\theta$는 업데이트할 매개변수

각 업데이트 단계에서 그래디언트는 이전 그래디언트($\gamma v_{t-1}$ 항)의 "미리 본" 현재 그래디언트($\eta \nabla_{\theta} J(\theta - \gamma v_{t-1})$ 항)의 조합으로 계산되며, 이를 통해 매개변수 $\theta$가 업데이트된다. 이 방식은 그래디언트의 변동을 완화하고, 경사 하강법의 수렴을 가속화하는 데 도움이 된다.

06.Adagrad(Adaptive Gradient, 2011)

SGD, Momentum, NAG 모두 모든 파라미터 업데이트에 동일한 learning rate 값을 적용
학습률이 너무 작으면 학습시간이 길고, 너무 크면 발산해서 학습이 제대로 이루어지지 않는 문제가 있다.

AdaGrad는 모든 파라미터에 대해 동일한 학습률을 적용하는 대신 경사의 크기에 따라 학습률을 조정하여 개선하고자 하였다.
많이 움직이는 파라미터의 학습률은 작게, 적게 움직이는 파라미터의 학습률은 크게 조정하여 각 파라미터에 맞는 학습률을 동적으로 적용한다.

수식

$E[g^2]_t = E[g^2]_{t-1} + (1-\gamma) g^2_t$
$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_t$

• 여기서 $G_t$는 시간 $t$에서의 누적 제곱 그래디언트, $\nabla J$는 비용 함수의 그래디언트, $\theta_t$는 시간 $t$에서의 파라미터, $\eta$는 학습률, $\epsilon$은 0으로 나누는 것을 방지하기 위한 작은 상수 (예: $10^{-6}$)이다.

하지만, Adagrad는 $t$가 증가함에 따라, $G_t$가 점점 커져서, learning rate가 점점 소실되는 문제가 있다.

07.RMSProp (Root Mean Square Propagation, 2012)

RMSProp은 AdaGrad의 학습률 감소 문제를 해결하기 위해 제안된 방법입니다. RMSProp는 누적 제곱 그래디언트 $G_t$를 계산할 때 모든 과거 그래디언트를 동일하게 고려하는 대신 최근의 그래디언트에 더 큰 가중치를 부여하는 지수 가중 평균 방식을 사용한다.

수식

$E[g^2]_t = \gamma E[g^2]_{t-1} + (1-\gamma) g^2_t$
$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_t$

• $\gamma$는 지수 가중 평균을 계산할 때 사용하는 감쇠 계수 (보통 forgetting factor 또는 decaying factor라고 부른다.)이다. 이 값은 0과 1 사이의 값이며, 값이 클수록 최근의 그래디언트에 더 큰 가중치를 부여한다.

$G_t = \gamma (\gamma G_{t-2} + (1-\gamma) (\nabla J)^2_{t-1}) + (1-\gamma) (\nabla J)^2$
$\gamma$는 0~1사이 이므로 오래된 데이터일수록 영향을 적게 미친다.

-> learning rate 소실문제를 해결

08.AdaDelta (2012)

AdaDelta는 RMSProp의 개선 버전으로, Adagrad의 학습률이 단조롭게 감소하는 것을 완화하기 위해 제안되었다.

수식(아직 이해X)

$E[\Delta\theta^2]_t = \gamma E[\Delta\theta^2]_{t-1} + (1-\gamma) \Delta\theta^2_t$
$RMS[\Delta\theta]_t = \sqrt{E[\Delta\theta^2]_t + \epsilon}$
$\Delta\theta_t = -\frac{RMS[\Delta\theta]_{t-1}}{RMS[g]_t} g_t$
$\theta_{t+1} = \theta_t + \Delta\theta_t$

Adadelta를 사용하면, 기본 학습률을 설정할 필요조차 없게 된다. 왜냐하면 이는 업데이트 규칙에서 제거되었기 때문이다.

09.Adam (2015)

Adam은 모멘텀과 RMSProp의 아이디어를 결합한 느낌
Momentum의 장점인 이전 그라디언트의 경향을 적용하면서, RMSProp의 장점인 learning rate가 점점 소실되는 문제를 해결하여 learning rate를 적절하게 조정한다.

$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$
$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$

$\hat{m}_t = \frac{m_t}{1 - \beta_1^t}$
$\hat{v}_t = \frac{v_t}{1 - \beta_2^t}$

수식

$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t$

 Adam의 최적화 갱신 경로를 살펴 보면, 기존의 모멘텀과 같이 오버슈팅을 하면서도 전역 최솟값을 향해 효율적으로 움직이는 것을 확인할 수 있다. 즉, 이는 앞서 언급한 모멘텀의 특징과 RMSProp의 특징 모두를 적용했다는 것을 말한다.

10.AdaMax

11.Nadam (2016)

Nadam은 Adam과 Nesterov Accelerated Gradient (NAG)의 장점을 결합한 최적화 알고리즘이다. Adam은 모멘텀과 RMSProp의 개념을 결합하여, 각 매개변수에 대해 학습률을 조정한다. 이는 매개변수의 스케일에 따라 학습률을 개별적으로 조정하므로, 최적화 과정이 더 안정적이고 빠르게 수렴한다.

그러나 Adam은 학습 동안 일정한 학습률을 유지하는 경향이 있어, 때때로 전역 최적해를 놓칠 수 있다. 이를 해결하기 위해 NAG의 개념을 도입한 것이 Nadam입니다. NAG는 현재의 기울기가 아닌, 모멘텀의 방향으로 조금 더 나아간 위치에서의 기울기를 사용하여 매개변수를 업데이트한다. 이는 미래의 위치를 예측하여, 최적화 과정을 더 빠르고 정확하게 만든다.

Nadam을 구현하기 위해서는 NAG의 업데이트 공식을 조금 수정해야 한다. 기존의 NAG에서는 이전 단계의 모멘텀을 사용하여 현재 위치에서의 기울기를 계산했다. 그러나 Nadam에서는 현재 단계의 모멘텀을 사용하여 미래의 위치에서의 기울기를 계산한다. 이는 미래의 모멘텀을 예측하는 효과를 가지며, 이를 통해 더 빠르고 정확하게 전역 최솟값을 찾을 수 있다.

이러한 개념을 Adam의 업데이트 공식에 적용하면, 각 매개변수에 대한 학습률을 동적으로 조정하면서도 미래의 위치를 예측하는 효과를 얻을 수 있다. 이로 인해, Nadam은 Adam보다 더 빠르고 정확하게 최적화 문제를 해결할 수 있다.

수식

NAG의 업데이트 공식은 다음과 같다.

1. $g_t = \nabla J(\theta_t - \gamma m_{t-1})$
2. $m_t = \gamma m_{t-1} + \eta g_t$
3. $\theta_{t+1} = \theta_t - m_t$

여기서, $g_t$는 현재 위치에서의 기울기, $m_t$는 모멘텀, $\theta_t$는 현재 위치, $\gamma$는 모멘텀 계수, $\eta$는 학습률을 나타낸다.

Adam의 업데이트 공식은 다음과 같다

1. $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{v_t} + \epsilon} m_t$

여기서, $v_t$는 가중치에 대한 2차 모멘트의 추정치, $\epsilon$은 0으로 나누는 것을 방지하는 작은 상수, $m_t$는 1차 모멘텀의 추정치를 나타낸다.

Nadam에서는 NAG의 업데이트 공식을 조금 수정하여 사용한다. 모멘텀 $m_t$를 이전 모멘텀 $m_{t-1}$ 대신 현재 모멘텀 $m_t$를 사용하여 미래의 모멘텀을 추정하는 효과를 얻는다. 이를 반영한 NAG의 업데이트 공식은 다음과 같다.

1. $g_t = \nabla J(\theta_t)$
2. $\theta_{t+1} = \theta_t - (\gamma m_t + \eta g_t)$

이 효과를 Adam에 적용하려면, Adam의 업데이트 공식을 먼저 풀어서 작성해야 한다.

$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{v_t} + \epsilon} \left(\beta_1 \frac{m_{t-1}}{1 - \beta_1^t} + (1 - \beta_1) \frac{g_t}{1 - \beta_1^t}\right)$

여기서 $\beta_1$는 1차 모멘텀의 지수 평균을 계산할 때 사용되는 감쇠 계수이다.

Nadam에서는 이 공식을 다음과 같이 수정하여 사용한다

$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{v_t} + \epsilon} \left(\beta_1 \frac{m_t}{1 - \beta_1^t} + (1 - \beta_1) \frac{g_t}{1 - \beta_1^t}\right)$

이렇게 수정하면, Adam의 업데이트 공식에서 미래의 모멘텀을 사용하는 효과를 얻을 수 있다.