Loss function
로스 펑션은 라벨값과 예측값의 차이를 로스(Loss)라고 말하고, 이들을 계산하기 위한 함수를 의미한다. 그리고 학습은 로스(Loss)를 최소화 하는 방향으로 가중치를 업데이트하며 진행된다.
학습의 진행이 로스(Loss)를 최소화 하는 방향으로 진행되기 때문에, Loss function을 제대로 정하는 것은 매우 중요하다. 같은 네트워크를 사용한다고 하더라도 로스 펑션을 바꾸면 가중치는 다른 값으로 업데이트가 진행되고 최종적으로 뉴럴넷의 성능이 달라지게 된다.
Classfication Loss
01.CrossEntropy Loss(nn.CrossEntropyLoss)
정의
CrossEntropy Loss는 두 확률 분포 사이의 차이를 측정하는 손실 함수입니다. 주로 분류 문제에서 사용됩니다.
구조
는 실제 분포의 확률, 는 모델이 예측한 확률
02.Connectionist Temporal Classification loss(nn.CTCLoss)
정의
CTC Loss는 시퀀스 학습 문제에서 사용되며, 정렬 없이 시퀀스를 학습할 수 있게 해줍니다. 이 손실 함수는 입력과 출력 시퀀스의 길이가 다를 때 유용하며, 주로 음성 인식이나 핸드라이팅 인식 같은 문제에서 사용됩니다. 수식은 복잡해서 여기에 나열하기 어렵지만, 기본적으로 가능한 모든 정렬을 고려하여 손실을 계산합니다.
03.Negative log likelihood loss(nn.NLLLoss)
정의
NLL Loss는 모델의 예측 확률 분포가 실제 데이터 분포를 얼마나 잘 반영하는지 측정하는 손실 함수입니다.
구조
는 특정 클래스에 대한 예측 로그 확률
04.Poisson Negative log likelihood loss (nn.PoissonNLLLoss)
정의
Poisson NLL Loss는 예측값이 포아송 분포를 따르는 회귀 문제에 사용되는 손실 함수
구조
여기서 는 예측값, 는 실제 값
05.Gaussian Negative log likelihood loss (nn.GaussianNLLLoss)
정의
Gaussian NLL Loss는 예측값이 가우시안 분포를 따르는 회귀 문제에 사용되는 손실 함수입니다.
구조
는 예측값, 는 실제 값, 는 예측 분산. 이 손실 함수는 모델이 예측값뿐만 아니라 예측의 불확실성도 추정할 수 있게 해줍니다.
06.Kullback-Leibler Divergence (KL Divergence) loss (nn.KLDivLoss)
정의
KL Divergence는 두 확률 분포 사이의 차이를 측정하는 손실 함수입니다. 주로 생성 모델에서 사용됩니다.
구조
는 실제 분포의 확률을, 는 모델이 예측한 확률
07.Binary Cross-Entropy Loss(nn.BCELoss)
정의
BCE Loss는 이진 분류 문제에서 사용되며, 각 클래스에 대한 확률을 독립적으로 모델링합니다.
구조
는 예측 확률, 는 실제 레이블(0 또는 1)
08.Binary Cross-entropy loss, on logits (nn.BCEWithLogitsLoss)
정의
BCEWithLogitsLoss는 BCELoss의 변형으로, 입력으로 로짓을 받아서 계산의 안정성을 높입니다. 로짓은 로지스틱 함수의 역함수로, 확률을 [0, 1]에서 [-∞, +∞]로 변환합니다.
구조
는 예측 로짓, 는 실제 레이블(0 또는 1)
09.Margin Ranking Loss(nn.MarginRankingLoss)
정의
Margin Ranking Loss는 두 입력 샘플 간의 상대적인 순위를 학습하는 손실 함수입니다.
구조
과 는 입력 샘플, 는 실제 순위(-1 또는 1), 은 마진
10.Hinge embedding loss (nn.HingeEmbeddingLoss)
정의
Hinge Embedding Loss는 두 입력 사이의 유사도를 학습하는 손실 함수입니다. 주로 이상치 탐지나 비지도 학습에서 사용됩니다.
구조
는 예측 유사도, 는 실제 유사도(1 또는 -1), 은 마진
11.MultiLabelMarginLoss(nn.MultiLabelMarginLoss)
정의
MultiLabelMarginLoss는 다중 레이블 분류 문제에 사용되는 손실 함수입니다. 각 샘플이 여러 레이블을 가질 수 있습니다.
구조
는 타겟 레이블에 대한 예측값, 는 다른 레이블에 대한 예측값
12.Two-class soft margin loss(nn.SoftMarginLoss)
정의
SoftMarginLoss는 이진 분류 문제에 사용되는 손실 함수로, 마진을 부드럽게 만들어 예측 오차에 대한 페널티를 줄입니다.
구조
는 예측값, 는 실제 레이블(-1 또는 1)
13.Multilabel soft margin loss (nn.MultiLabelSoftMarginLoss)
정의
MultiLabelSoftMarginLoss는 다중 레이블 분류 문제에 사용되는 손실 함수로, 각 샘플이 여러 레이블을 가질 수 있습니다.
구조
는 예측 확률, 는 실제 레이블(0 또는 1)
14.CosineEmbeddingLoss(nn.CosineEmbeddingLoss)
정의
CosineEmbeddingLoss는 두 입력 벡터의 코사인 유사도를 기반으로 손실을 계산하는 함수입니다. 주로 비지도 학습이나 이상치 탐지에서 사용됩니다.
구조
는 두 벡터의 코사인 유사도, 는 실제 유사도(1 또는 -1), 은 마진
15.Multi-class margin loss (nn.MultiMarginLoss)
정의
MultiMarginLoss는 다중 클래스 분류 문제에 사용되는 손실 함수입니다. 각 클래스에 대한 마진을 최대화하는 방향으로 학습합니다.
구조
는 타겟 클래스에 대한 예측값, 는 다른 클래스에 대한 예측값
16.TripletMarginLoss(nn.TripletMarginLoss)
정의
TripletMarginLoss는 트리플릿 학습 방법에 사용되는 손실 함수입니다. 트리플릿은 앵커(Anchor), 양성(Positive), 부정(Negative)의 세 가지 샘플로 구성되며, 앵커와 양성 사이의 거리는 가깝게, 앵커와 부정 사이의 거리는 멀게 학습합니다.
구조
는 앵커, 는 양성, 는 부정 샘플
17.TripletMarginWithDistanceLoss(nn.TripletMarginWithDistanceLoss)
정의
TripletMarginWithDistanceLoss는 TripletMarginLoss와 비슷하지만, 거리 함수를 사용자 정의할 수 있는 장점이 있습니다.
구조
는 앵커, 는 양성, 는 부정 샘플을 나타냅니다. 는 사용자 정의 거리 함수
18.Categorical Cross-Entropy Loss
정의
Categorical Cross-Entropy Loss는 다중 클래스 분류 문제에 사용되는 손실 함수입니다. 각 클래스에 대한 확률을 모델링합니다.
구조
는 실제 레이블의 원-핫 인코딩, 는 예측 확률
19.Log Loss
정의
Log Loss는 이진 분류 문제에 사용되는 손실 함수로, Binary Cross-Entropy Loss와 유사합니다.
구조
는 실제 레이블(0 또는 1), 는 예측 확률
Regression Loss
01.L1 Loss : MAE, Mean Absolute Error(nn.L1Loss)
정의
Mean Absolute Error(L1 Loss)는 예측값과 실제 값 사이의 절대적인 차이를 계산하는 손실 함수입니다. 이는 outlier에 대해 상대적으로 robust한 손실 함수이다. , V자 모양으로 미분이 불가능한 지점이 있다.
구조
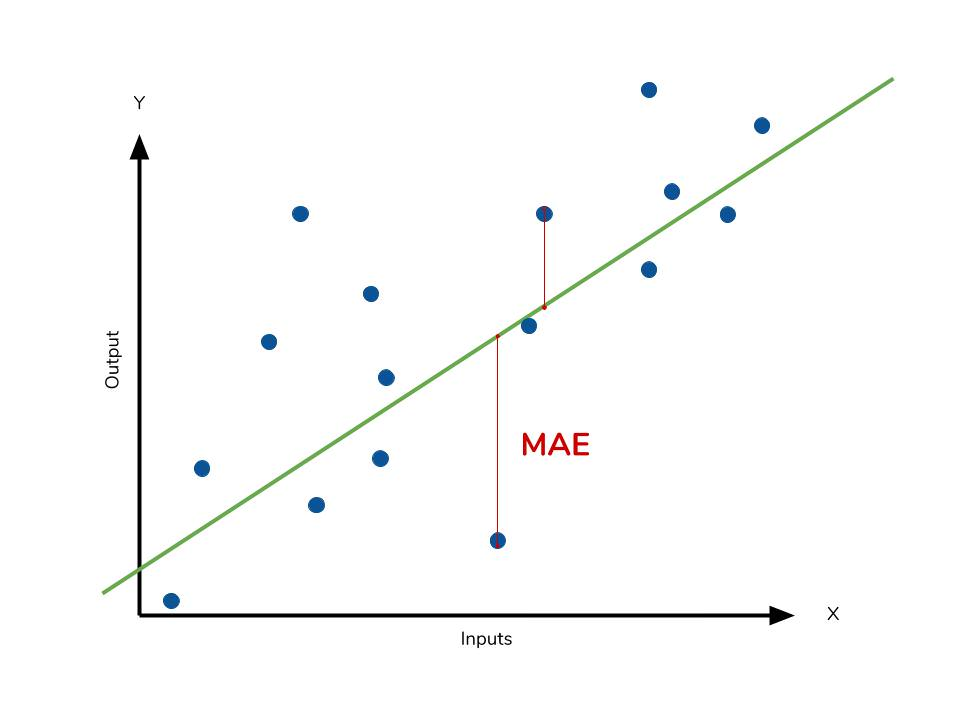
는 실제 값, 는 예측값
02.L2 Loss : MSE, Mean Squared Error(nn.MSELoss)
정의
Mean Squared Error(MSE Loss)는 예측값과 실제 값 사이의 제곱 차이를 계산하는 손실 함수이다. 이는 outlier에 민감한 손실 함수이다.
구조

는 실제 값, 는 예측값
03.Smooth MAE: Smooth L1 (nn.SmoothL1Loss)
정의
Smooth MAE 또는 Smooth L1 Loss는 L1 Loss와 비슷하지만, 예측 오차가 작은 경우에는 제곱 오차를, 큰 경우에는 절대 오차를 계산하여 손실을 부드럽게 만드는 함수이다.
구조
여기서 는 실제 값, 는 예측값
04.Huber loss (nn.HuberLoss)
정의
Huber Loss는 MSE와 MAE를 결합한 손실 함수로, 예측 오차가 작은 경우에는 제곱 오차를, 큰 경우에는 절대 오차를 계산한다. 이는 이상치에 대해 더 강건한 모델을 만드는 데 도움이 된다.
구조
여기서 는 실제 값, 는 예측값, 는 임계값
특징
이 손실 함수는 이상치에 강건한 회귀 모델을 만들기 위해 1964년 "Robust Estimation of a Location Parameter" 논문에서 처음 소개되었다. 최근에는 강화 학습에서도 사용되는데, 특히 "Deep Q-Network" (DQN)이라는 아키텍처에서 사용되었다.
Huber vs. Smooth L1
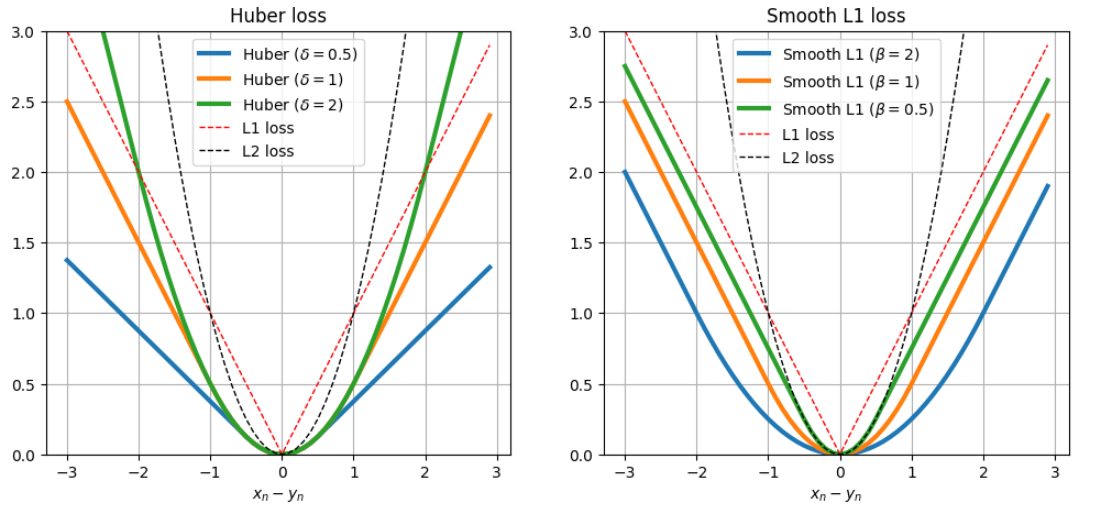
Huber loss는 가 커질수록 이차식에 가까워지며, 가 작아질수록 일차식에 가까워지지만 기울기가 감소하는 형태를 가진다. 반면 Smooth L1 loss는 값과 무관하게 기울기가 1에 가깝다. 가 작아질수록 L1 loss와 동일해지며, 가 커질수록 0 부근에서의 smoothness가 증가한다.
Regression Loss(additional)
01.RMSE(Root Mean Squared Error)
정의
RMSE는 MSE (Mean Squared Error)의 제곱근으로, 예측값과 실제값 간의 차이를 제곱하여 평균을 낸 후, 이 값을 제곱근하여 계산한다. 이는 오차의 제곱을 보정하여 실제 오차와 비슷한 스케일을 가진 값을 얻기 위함이다.
구조
는 실제값, 는 예측값, 은 데이터의 개수
02.MSLE(Mean Squared Log Error)
정의
MSLE는 예측값과 실제값의 로그를 취한 후 그 차이를 제곱하여 평균을 낸 값이다. 이는 비교적 큰 값에 대한 오차보다 작은 값에 대한 오차에 더 큰 가중치를 주는 특성이 있다.
구조
는 실제값, 는 예측값, 은 데이터의 개수
03.MAPE(Mean Absolute Percentage Error)
정의
MAPE는 예측값과 실제값의 차이를 실제값으로 나눈 후, 이를 절대값으로 변환하여 평균을 낸 값이다. 이는 예측 오차를 퍼센트로 표현하여, 상대적인 오차를 측정하는 데 사용된다.
구조
는 실제값, 는 예측값, 은 데이터의 개수
04.MPE(Mean Percentage Error)
정의
MPE는 예측값과 실제값의 차이를 실제값으로 나눈 후, 이를 평균한 값이다. 이는 MAPE와 비슷하지만, 절대값을 취하지 않아 오차의 방향성을 고려할 수 있다.
구조
는 실제값, 는 예측값, 은 데이터의 개수
