Probability and Likelihood

확률(Probability)

사전에 정의된 매개변수의 분포를 가진 시행에서 특정 결과가 발생할 기회를 수량화한다. 예를 들어, 주사위를 굴릴 때 특정 숫자가 나올 확률이나, 동전을 10번 던져서 앞면이 나올 횟수의 확률을 계산할 수 있다.

가능성(Likelihood)

관측된 데이터가 주어졌을 때, 그 데이터가 특정 매개변수의 모델에서 나올 "가능성"을 나타낸다. 가능성은 특정 매개변수 값이 주어진 모델이 관측된 데이터를 얼마나 잘 설명하는지를 측정한다.

• 확률은 사전에 특정 결과가 일어날 가능성을 말하며, 이산 사건 또는 연속 사건에 대한 기대를 정량화한다.
  우도는 주어진 파라미터가 실제 관측된 데이터를 얼마나 잘 설명하는지 나타내며, 주로 모델의 파라미터를 추정한다.

이산사건과 연속사건의 비교

이산 사건에서의 Probability과 Likelihood

이산 사건은 명확하게 구분 가능한 결과를 가지는 사건이다. 예를 들어, 주사위를 던지거나 동전을 던지는 경우가 이에 해당한다.

확률

• 이산 확률은 각 결과가 발생할 확률을 명확히 할당할 수 있다. 예를 들어, 공정한 주사위를 던질 때 특정 숫자가 나올 확률은 정확히 1/6이다. 모든 사건의 확률을 더 하면 1이 된다.

$P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}$

Likelihood

• 이산 사건에서의 Likelihood는 주어진 모델 또는 파라미터가 관측된 데이터를 얼마나 잘 설명하는지를 측정한다. 예를 들어, 여러 번의 주사위 던지기에서 나온 결과가 특정 주사위 모델(예: 주사위가 편향되었을 가능성)을 얼마나 잘 지지하는지를 나타낼 수 있다.

연속 사건에서의 Probability과 Likelihood

연속 사건은 결과가 연속적인 값들의 범위로 표현될 수 있는 사건이다. 예를 들어, 사람의 키를 측정하는 것이나 온도를 측정하는 것이 이에 해당한다.

Probability

• 연속 확률은 확률 밀도 함수(Probability Density Function, PDF)를 사용하여 표현된다. 특정 정확한 값에 대한 확률은 0이지만, 값의 범위에 대한 확률은 PDF를 통해 계산될 수 있다. 예를 들어, 어떤 지역의 평균 기온이 20°C에서 25°C 사이일 확률을 구할 수 있다.

Likelihood

• 연속 사건에서의 Likelihood 역시 특정 파라미터 값이 주어졌을 때 관측된 데이터의 합리성을 측정합니다. 이 경우, 우도는 데이터 포인트가 모델의 PDF에 의해 얼마나 잘 설명되는지를 나타내는 값입니다. 예를 들어, 정규 분포를 가정할 때 특정 평균과 표준편차를 가진 정규 분포 모델이 주어진 데이터를 얼마나 잘 설명하는지를 Likelihood로 계산할 수 있다.

결론

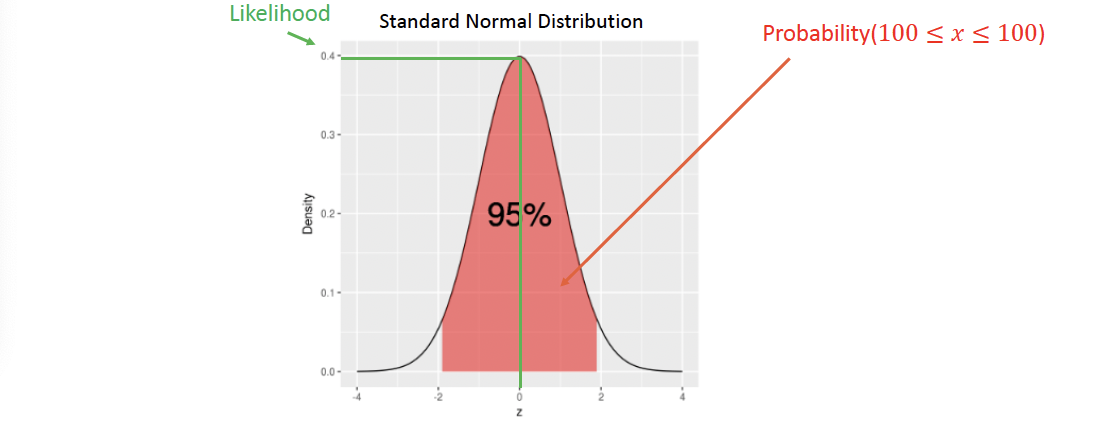
이산 및 연속 사건에서 Probability는 사건의 가능성을 측정하는 반면, Likelihood는 주어진 모델이나 파라미터 세트가 관참된 데이터를 어떻게 설명하는지를 나타내는 척도이다. 확률은 주로 사전 지식을 바탕으로 한 예측에 사용되고, 우도는 주어진 데이터를 가지고 모델을 평가하는 데 사용된다. 이러한 개념은 통계적 추론, 특히 모델 선택과 파라미터 추정에서 중요한 역할을 한다.

갱신

Probability와 Likelihood는 서로 다른 맥락에서 갱신될 수 있다. 이 두 개념을 어떻게 갱신하는지 구체적으로 살펴보자.

Probability 갱신

Probability는 베이즈 통계에서 주로 갱신된다. 베이즈 정리를 사용하면 사전 확률(Prior Probability)과 새로운 증거(새로운 데이터)를 통합하여 사후 확률(Posterior Probability)을 계산할 수 있다. 이 과정에서 새로운 정보가 들어오면 확률 값이 업데이트된다. 예를 들어, 어떤 질병에 걸릴 확률을 알고 있을 때 새로운 검사 결과가 그 확률을 갱신하는 데 사용될 수 있다.

Likelihood 갱신

Likelihood는 특정 모델 또는 파라미터에 대한 데이터의 지지도를 나타내며, 직접적인 확률 값이 아니다. 새로운 데이터가 관찰될 때마다 Likelihood는 계산되어 해당 모델 또는 파라미터 설정이 얼마나 잘 데이터를 설명하는지를 평가한다. 그러나 Likelihood 자체는 "갱신"되지 않는다. 대신, 새로운 데이터가 추가될 때마다 새로운 Likelihood 값이 계산되어 모델의 적합도를 다시 평가할 수 있다.

결론

따라서, Probability는 새로운 정보를 받을 때마다 베이즈적 방식으로 갱신된다. 반면, Likelihood는 새로운 데이터가 주어질 때마다 다시 계산되어 모델 또는 파라미터의 적합도를 평가한다. Likelihood 자체는 이전 값에 대한 업데이트가 아니라 각 데이터 세트에 대해 새로 계산되는 값이다.

PDF:Probability Density Function(확률밀도함수)

• 확률밀도함수는 연속적인 사건의 확률을 설명할 때 사용된다. 예를 들어, 1과 6 사이의 수를 무작위로 선택할 때 특정 숫자를 선택할 확률은 0이지만, 특정 구간에 속하는 숫자를 선택할 확률은 0이 아닐 수 있다. 이때 PDF를 사용하여 특정 구간 내에서 변수가 취할 수 있는 값의 확률을 설명할 수 있다.

MLE(최대 가능도 추정)

• Maximum Likelihood Estimation, MLE: 모수와 파라미터의 정보가 없는 데이터 집합을 가장 잘 설명하는(likelihood가 최대인) 모델 매개변수(예: 정규분포의 평균과 분산)를 찾는 방법이다.
• 이 방법은 특정한 분포(예: 정규분포, 이항분포 등)를 가정하고, 그 분포의 매개변수를 조정하여 관측된 데이터가 나타날 가능도를 최대화하는 매개변수 값을 찾는다.

Likelihood 함수 $L(\theta \mid X)$

우도 함수는 파라미터 ( \theta )가 주어졌을 때 관측된 데이터 ( X )가 나타날 확률을 나타냅니다. 데이터 포인트들이 독립적일 때, 전체 데이터 세트에 대한 우도는 각 데이터 포인트의 확률을 곱한 것과 같다:

$L(\theta \mid X) = P(X \mid \theta) = \prod_{i=1}^n P(x_i \mid \theta)$
여기서 $n$은 데이터 포인트의 수이며, $x_i$는 개별 데이터 포인트이다.

로그 우도 함수

계산을 단순화하기 위해, 우도 함수의 로그를 취하는 것이 일반적이다. 로그는 증가 함수이기 때문에 우도 함수를 최대화하는 것과 로그 우도 함수를 최대화하는 것은 동일한 $\theta$ 값을 결과로 한다. 로그를 취하면 곱셈이 덧셈으로 변환되어 계산이 간단해진다.

$\log L(\theta \mid X) = \sum_{i=1}^n \log P(x_i \mid \theta)$

MLE의 최적화

로그 우도 함수를 $\theta$에 대해 최대화하는 $\theta$ 값을 찾기 위해, 미분을 사용하여 첫 번째 도함수를 0으로 설정하고 이를 $\theta$에 대해 푼다. 이 과정을 통해 최적의 파라미터 $\theta$ 추정값을 얻을 수 있다.

예시

정규 분포의 경우, 평균 $\mu$와 분산 $\sigma^2$를 파라미터로 가지며, MLE를 사용하여 이 파라미터들을 추정할 수 있다. 이 때, 관측된 데이터의 평균을 최적의 $\mu$로, 데이터의 분산을 최적의 $\sigma^2$로 설정하는 것이 일반적인 결과이다.

코드 구현

MLE 계산

정규 분포 아래에서 관측치의 우도(Likelihood)를 계산하는 방법을 알아보자. 정규 분포는 평균 $\mu$와 표준편차 $\sigma$로 정의된다. 이 분포를 사용하여 단일 관측치의 우도를 계산하는 방법은 다음과 같다.

1단계: 지수(exponent) 계산

• 관측값 $x$와 평균 $\mu$ 사이의 차이를 계산한다.
• 이 차이를 제곱한 다음, 2와 $\sigma^2$로 나눈다.
• 이 결과에 음수를 취합니다.

$\text{exponent} = -\frac{(x - \mu)^2}{2\sigma^2}$

2단계: 우도 업데이트

• 계산된 지수를 사용하여 우도를 업데이트한다. 정규 분포의 확률 밀도 함수(PDF) 공식을 사용한다.

$f(x \mid \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{\text{exponent}}$

• 여기서 $\frac{1}{\sqrt{2\pi\sigma^2}}$는 정규화 상수로, 모든 확률의 합이 1이 되도록 보장한다.

따라서, 특정 관측값 $x$의 우도는 평균 $\mu$와 표준편차 $\sigma$가 주어진 정규 분포에서 위의 식을 사용하여 계산된다. 이 우도 값은 그 관측치가 주어진 $\mu$와 $\sigma$를 가진 정규 분포에서 얼마나 일반적인지, 또는 얼마나 이례적인지를 수치적으로 나타낸다.

이 계산법은 최대 우도 추정(MLE)에서 중요한 단계이다. 데이터 집합 전체에 대한 우도를 최대화하는 $\mu$와 $\sigma$ 값을 찾기 위해 사용된다. 각 관측치에 대해 우도를 계산하고, 이들을 곱하여 전체 데이터 세트의 우도를 얻으며, 이를 최대화하는 파라미터를 찾는다.

전체 코드

import math
##### Sample Dataset (10) #####
measurements = [2.1, 2.2, 2.0, 2.3, 2.1, 2.2, 2.1, 2.4, 2.3, 2.2]
##### Function: :Likelihood calculation #####
def calculate_likelihood(data, mu, sigma):
    likelihood = 1.0
    for measurement in data:
        exponent = -(measurement-mu)**2/(2*sigma**2)
        likelihood *= (1/(sigma*math.sqrt(2*math.pi)))*math.exp(exponent)
    return likelihood

### 1. Calculate the likelihood ###
print("### 1. Calculate the likelihood ###")
# 모수의 평균을 2.2라고 가정한 값
mean = 2.2
# 표준편차 역시 가정한 값
std_dev = 0.1
# 계산
likelihood = calculate_likelihood(measurements, mean, std_dev)
# 만일 mean이 2.2이고 std_dev이 0.1일 likelyhood
print("Likelihood:", likelihood)

### 2. Calculate the likelihoods by changing mean values ###
print("### 2. Calculate the likelihoods by changing mean values ###")
# 직관을 위해 가정 값을 여러개 두자
mean_list = [2.0, 2.1, 2.2, 2.3, 2.4]
std_dev = 0.1
# 계산
for mean in mean_list:
    likelihood = calculate_likelihood(measurements, mean, std_dev)
    # 각각의 평균과 편차에 대한 likelyhood 
    print(f"Mean: {mean}, Likelihood: {likelihood}")

### 3. Calculate the likelihoods by changing both mean and std values ###
print("### 3. Calculate the likelihoods by changing both mean and std values ###")
# 두개를 다 돌려보자
mean_list = [2.0, 2.1, 2.2, 2.3, 2.4]
std_dev_list = [0.1, 0.2, 0.3, 0.4, 0.5]
# Calculate the likelihoods by changing both mean and std values
for mean in mean_list:
    for std_dev in std_dev_list:
        likelihood = calculate_likelihood(measurements, mean, std_dev)
        # 각각의 평균과 편차에 대한 likelyhood 
        print(f"Mean: {mean}, std:{std_dev}, Likelihood: {likelihood}")

import numpy as np
### 4. Maximum likelihood estimation ###
print("### 4. Maximum likelihood estimation ###")
max_likelihood = -99
for mean in np.arange(2, 3, 0.001):
    for std in np.arange(0.1, 0.5, 0.001):
        likelihood = calculate_likelihood(measurements, mean, std)
        if max_likelihood < likelihood:
            max_likelihood = likelihood
            best_mean = mean
            best_std_dev = std

print("Maximum Likelihood Estimation:")
print(f"Best Mean: {best_mean}")
print(f"Best Standard Deviation: {best_std_dev}")
print(f"Max Likelihood: {max_likelihood}")