인간 ALU

김민욱·2025년 10월 17일
RISC-Vcomputer architecture

컴퓨터구조 - Computer Architecture(RISC-V)

목록 보기
11/11

1. 151과 241이라는 signed 8-bit decimal이 2의 보수법 포맷으로 저장되어 있다. 151 + 214를 saturating arithmetic으로 계산하여 과정을 보이고 결과를 decimal로 작성하라.

151 = 10010111
two's complement: 10010111 = 1+2+4+16-128 = -105

241 = 11110001
two's complement: 11010110 = 2+4+16+64-128 = -42

2. 다음 곱셈기의 octal unsigned 8-bit integer 62와 12 계산 과정을 표를 사용해 보여라.

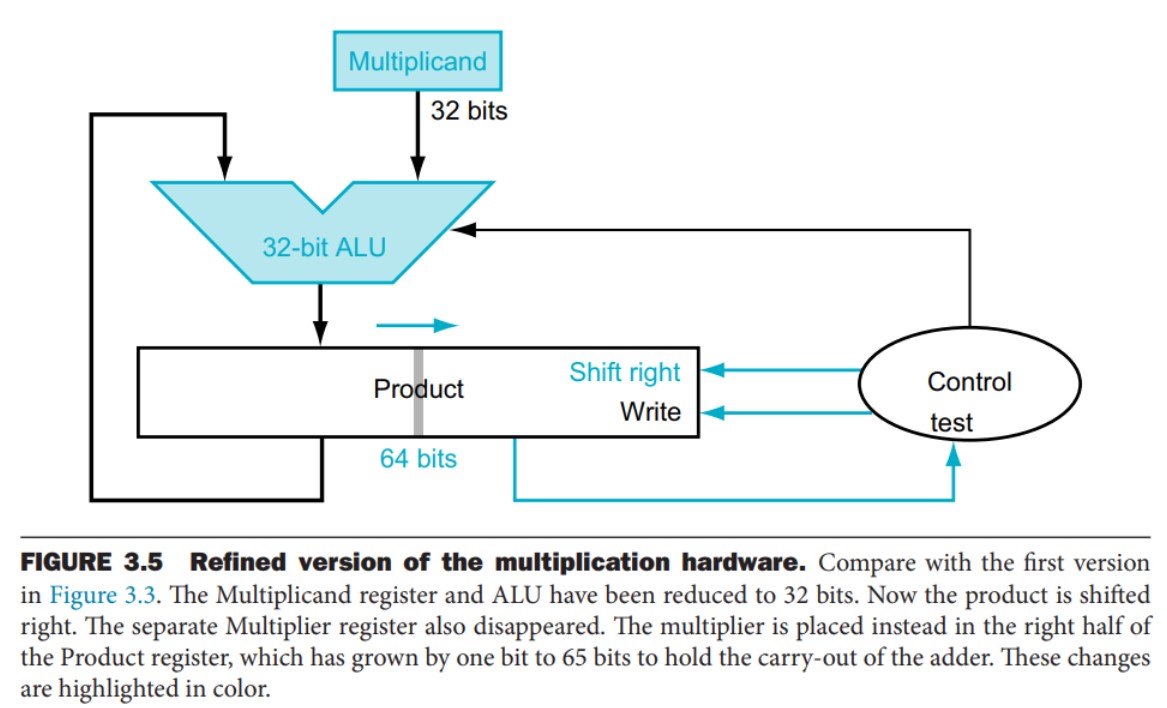
62(o) * 12(o) = 50 * 10 = 00110010(2) * 00001010(2)

IterationStepMultiplicand (8-bit)Product (16-bit)
0Initial values001100100000000000001010
11: 0 => No Operation001100100000000000001010
2: Shift right Product001100100000000000000101
21a: 1 => Prod[15:8] = Prod[15:8] + Mcand001100100011001000000101
2: Shift right Product001100100001100100000010
31: 0 => No Operation001100100001100100000010
2: Shift right Product001100100000110010000001
41a: 1 => Prod[15:8] = Prod[15:8] + Mcand001100100011111010000001
2: Shift right Product001100100001111101000000
51: 0 => No Operation001100100001111101000000
2: Shift right Product001100100000111110100000
61: 0 => No Operation001100100000111110100000
2: Shift right Product001100100000011111010000
71: 0 => No Operation001100100000011111010000
2: Shift right Product001100100000001111101000
81: 0 => No Operation001100100000001111101000
2: Shift right Product001100100000000111110100

result: 0000000111110100(2) = 500

3. IEEE 754-2008은 16-bit 길이의 half precision이 존재했다. 제일 왼쪽 비트는 sign bit, 5-bit Exponent field, bias 15, 10-bit mantissa field, hidden bit 1로 구성되어 있다.
−1.5625×10−1-1.5625\times10^{-1}을 half precision 포맷으로 나타내어라. 이 때 exponent 저장은 excess-16 포맷으로 한다. 그리고 해당 표현의 range와 정밀도를 IEEE 754 std single precision과 비교하여라.

(−1)s×(1+Frac)×2(E−bias)(-1)^s\times(1+Frac)\times2^{(E-bias)}
1.5625×10−1=0.00101→1.01×2−31.5625\times10^{-1}=0.00101 \rarr 1.01\times2^{-3}
E−bias=E−16=−3⇒E=13=01101E-bias=E-16=-3 \Rarr E=13=01101
(because we use excess-16)
s: 1
Fraction: 0100000000
Exponent: 01101

(−1)×(1.01)×2−3⇒1011010100000000(-1)^\times(1.01)\times2^{-3}\Rarr 1011010100000000

Single precision has 8 bits wide Exponent field. And its bias is 127. So single precision has wider exponent range than half precision.
Single precision has 23 bits wide Fraction field.
So It can represent mantissa with more precision.

4. 아래 식을 손으로 계산하라. 각 값은 위 문제에서 설명한 16-bit half precision 포맷으로 저장된다고 가정하고 1 guard, 1 round, 1 sticky bit를 가지고 있으며 nearest even rounding을 사용한다고 가정한다. 모든 과정을 보이고 답을 16-bit floating point 포맷과 decimal로 작성하라.

(3.984375×10−1+3.4375×10−1)+1.771×103(3.984375\times10^{-1}+3.4375\times10^{-1})+1.771\times10^3

First, 3.984375×10−1+3.4375×10−13.984375\times10^{-1}+3.4375\times10^{-1}

step 0) Convert to binary format
3.984375×10−1=0.3984375→0.0110011=1.10011×2−23.984375\times10^{-1} = 0.3984375 \rarr 0.0110011=1.10011\times2^{-2}
3.4375×10−1=0.34375→0.01011=1.01100×2−23.4375\times10^{-1}=0.34375 \rarr 0.01011=1.01100\times2^{-2}
step 1) Align binary point
Both exponent is same. We don't need to align this.
step 2) Add significands
1.10011×2−2+1.01100×2−2=10.11111×2−21.10011\times2^{-2}+1.01100\times2^{-2}=10.11111\times2^{-2}
step 3) Normalize
10.11111×2−2=1.011111×2−110.11111\times2^{-2}=1.011111\times2^{-1}
step 4) Round
We don't need to round up or down.

The result is
1.011111×2−1=(1+14+18+116+132+164)×2−1=0.7421875=7.421875×10−11.011111\times2^{-1} \\= (1+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64})\times2^{-1}\\ =0.7421875=7.421875\times10^{-1}

Next, 7.421875×10−1+1.771×1037.421875\times10^{-1} + 1.771\times10^3

step 0) Convert to binary format
7.421875×10−1→1.011111×2−17.421875\times10^{-1}\rarr 1.011111\times2^{-1}
1.771×103=1771.0→011011101011=1.1011101011×2101.771\times10^3 = 1771.0 \rarr 011011101011=1.1011101011\times2^{10}
step 1) Align binary point
Difference between two exponents is 10−(−1)=1110-(-1)=11.
1.011111×2−1>>11=0.00000000001011111×2101.011111\times2^{-1} >> 11=0.00000000001011111\times2^{10}
The length of Fraction field is 10-bit. We need to round.

guard bit = 1, round bit = 0, sticky bit = 1
So we add 1 to lsb of Fraction field.

0.00000000001011111×210→0.0000000001×2100.00000000001011111\times2^{10} \rarr 0.0000000001\times2^{10}
step 2) Add significands
0.0000000001×210+1.1011101011×210=1.1011101100×2100.0000000001\times2^{10}+1.1011101011\times2^{10}=1.1011101100\times2^{10}
step 3) Normalize and Round
We don't need to normalize and round.

The result is
1.1011101100×210=(1+12+18+116+132+1128+1256)×210=1.772×1031.1011101100\times2^{10}\\=(1+\frac{1}{2}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{128}+\frac{1}{256})\times2^{10}\\=1.772\times10^{3}

In decimal, 1772.
In 16-bit floating point format,
sign bit = 0,
Exponent field = 10 + bias = 10 + 15 = 25 = 11001(2)
Fraction field = 1011101100(2)
So, 0110011011101100

5. 아래 식을 손으로 계산하라. 각 값은 위 문제에서 설명한 16-bit half precision 포맷으로 저장된다고 가정하고 1 guard, 1 round, 1 sticky bit를 가지고 있으며 nearest even rounding을 사용한다고 가정한다. 모든 과정을 보이고 답을 16-bit floating point 포맷과 decimal로 작성하라.

3.984375×10−1+(3.4375×10−1+1.771×103)3.984375\times10^{-1}+(3.4375\times10^{-1}+1.771\times10^3)

First, 3.4375×10−1+1.771×1033.4375\times10^{-1}+1.771\times10^3

step 0) Convert to binary format
3.4375×10−1=0.34375→0.01011=1.01100×2−23.4375\times10^{-1}=0.34375 \rarr 0.01011=1.01100\times2^{-2}
1.771×103=1771.0→011011101011=1.1011101011×2101.771\times10^3 = 1771.0 \rarr 011011101011=1.1011101011\times2^{10}
step 1) Align binary point
Difference between two exponents is 10−(−2)=1210-(-2)=12.
1.01100×2−2>>12=0.00000000000101100×2101.01100\times2^{-2} >> 12 = 0.00000000000101100\times2^{10}

The length of Fraction field is 10-bit. We need to round.

guard bit = 0, round bit = 1, sticky bit = 1

According to the round to the nearest even rule, we don't round up in this case.

0.00000000000101100×210→0.0000000000×210=00.00000000000101100\times2^{10}\rarr0.0000000000\times2^{10}=0
step 2) Add significands
0.0000000000×210+1.1011101011×210=1.1011101011×2100.0000000000\times2^{10}+1.1011101011\times2^{10}=1.1011101011\times2^{10}
step 3) Normalize and Round
We don't need to do.

The result is
1.1011101011×210=1.771×1031.1011101011\times2^{10}\\=1.771\times10^{3}

Next, 3.984375×10−1+1.771×1033.984375\times10^{-1}+1.771\times10^3

step 0) Convert to binary format
3.984375×10−1=0.3984375→0.0110011=1.10011×2−23.984375\times10^{-1} = 0.3984375 \rarr 0.0110011=1.10011\times2^{-2}
1.771×103=1771.0→1.1011101011×2101.771\times10^3 = 1771.0 \rarr 1.1011101011\times2^{10}
step 1) Align binary point
Difference between two exponents is 10−(−2)=1210-(-2)=12.
1.10011×2−2>>12=0.00000000000110011×2101.10011\times2^{-2}>>12=0.00000000000110011\times2^{10}

The length of Fraction field is 10-bit. We need to round.

guard bit = 0, round bit = 1, sticky bit = 1

According to the round to the nearest even rule, we don't round up in this case.

0.00000000000110011×210→0.0000000000×210=00.00000000000110011\times2^{10} \rarr 0.0000000000\times2^{10}=0
step 2) Add significands
0.0000000000×210+1.1011101011×210=1.1011101011×2100.0000000000\times2^{10}+1.1011101011\times2^{10}=1.1011101011\times2^{10}
step 3) Normalize and Round
We don't need to do.

The result is
1.1011101011×210=1.771×1031.1011101011\times2^{10}\\=1.771\times10^{3}

In decimal, 1771.
In 16-bit floating point format,
sign bit = 0,
Exponent field = 10 + bias = 10 + 15 = 25 = 11001(2)
Fraction field = 1011101011(2)
So, 0110011011101011(2).

profile
김민욱
이전 포스트

인간 컴파일러

0개의 댓글