탐색적 자료 분석

1) 일반적으로 시계열에 사용되는 데이터 응용기법
: 히스토그램, 도표 그리기, 그룹화 연산이 시계열 데이터에 어떻게 적용되는 지 살펴봄.
2) 시계열 분석의 근본적인 시간 기법
: 데이터가 서로 시간 관계가 있는 사오항에서만 의미 있음

탐색적 기법을 시계열 데이터셋에 적용하는 방법

데이터를 처음 마주하면,

1) 긴밀한 상관관계를 가지는 열이 있는지 확인
2) 관심 대상 변수의 전체 평균과 분산은 무엇인지 파악

를 파악하는데, 이는 '도표 그리기, 요약 통계 내기, 히스토그램 적용, 산점도 사용' 등으로 해결 가능

• 시간관련 질문
  1) 분석값의 범위가 무엇인지? 다른 논리적 단위나 기간에 따라 값이 달라지는가?
  2) 데이터가 일관성을 갖고 균등하게 측정됐는가? 아니면 시간이 흐르면서 측정이나 동작
  방식에 변화가 있었는가?
  를 파악하기 위해서는 히스토그램, 산점도, 요약 통계 같은 방법에 시간축을 함께 고려해야함.
  -> 히스토그램이나 산점도에 적용된 것 처럼 시간을 통계에 포함해야함.
  이때 시간은 그래프의 한 축 또는 그룹화 연산에 대한 하나의 그룹이 됨.

시계열에 특화된 탐색법

1. 정상성(stationarity)

: 시계열이 정상성이 된다는 의미와 정상성에 대한 통계적 검사
: 안정성의 수준을 의미
: 시계열을 다룰 때 처음으로 ""시계열이 시스템의 '안정성(stable)'을 반영하는가 아니면 지속적
인 변화를 반영하는가"" 의 질문을 던져 안정성의 수준(= 정상성)을 평가해야함. (d/t 시스템이
보여준 과거의 장기적 행동은 미래의 장기적인 행동을 얼마나 반영하는지 알아야하기 때문.)
-> 시계열의 '안정성'을 측정한 후, 내부적인 역학의 존재를 결정해야함.(ex. 계절변화)
= 자체상관을 찾는 과정

2. 자체상관(self correlation)

: 시계열 그 자체로 연관성이 있다는 의미와 이 연관성이 시계열의 내재된 역동성에 대해 보여주고
자 하는 것
: 미래의 데이터 예측에 먼 과거 또는 최근의 데이터가 얼마나 밀접한 연관성을 가지는지와 같은
근본적인 질문에 답을 구할 수 있음
-> 특정 행동역학을 발견했다면, 그 역학이 내가 알고자하는 인과관계에 어떠한 의미도 가지지 않
는다면??
-> 그 역학에 기반한 인과관계를 찾으려고 해서는 안됨. 따라서 상관관계가 곧 인과관계
는 아니라는 "허위상관"을 찾아야함.

3. 허위상관(spurious correlation)

: 상관관계가 허위가 된다는 의미와 허위상관을 마주칠 만한 상황

위 개념을
1. 롤링윈도와 확장 윈도 함수,
2. 자체상관함수(self correlation function),
3. 자기상관함수(autocorrelation function),
4. 편자기상관함수(portial autocorrelation function) 의 기법에 적용한다.

상성

많은 전통적인 시계열 모델은 정상화된 시계열에 의존함.
일반적으로 정상 시계열은 시간이 경과하더라도 꽤 안정적인 통계적 속성을 가지는데, 특히 평균과
분산에서 더욱 그러함.

1. 직관적인 정의

정상 시계열에서 측정된 시계열은 시스템의 안정적인 상태를 반영함.
그렇다면 데이터의 흐름이 정상이 아님을 보여주는 특징은 무엇이 있을까?

1) 평균값이 일정하게 유지되기 보다는 시간에 따라 증가함
2) 연간 최고점과 최저점 사이의 간격이 증가하므로 분산이 시간에 따라 증가함
3) 강한 계절성이 존재함.

2. 정상성의 정의와 증강된 디키-풀러 검정

정상과정 : 모든 시차 k에 대해 $y_t, y_{t+1},\cdot\cdot\cdot,y_{t+k}$의 분포가 t에 의존적이지 않은 것.

정상성의 통계적 검정은 unit root의 존재 유무라는 질문으로 이어짐.
unit root의 결여가 정상성을 증명하는 것은 아니지만, unit root가 있는 선형 시계열은 비정상으로
볼 수 있음.
정상성을 다루기 위한 일반적인 질문은 아직 정해진게 없고, 특정 과정에 unit root가 있음을 결정하는
것은 아직 정해진 바 없음.
"random walk(확률 보행)"의 예로부터 unit root에 대해서 간단한 직관 얻을 수 있음.
$y_t = \phi \times y_{t-1} + e_t$
이 과정에서 특정시간에 대한 실계열값은 직전 시간과 임의의 에러 함수임.

$\phi$값이 1이라면, unit root가 있다는 의미이고 정상보다는 run away(제멋대로)일 것임.
정상이 아닌 시계열이 반드시 추세를 가져야하는 것은 아님.
random walk는 근본적인 추세가 없는 비정상 시계열의 좋은 예임.
augmented Dickey-Fuller(ADF)검정 : 시계열의 정상성 문제를 가장 보편적으로 평가하는 평가
지표. 시계열에 unit root가 존재한다는 귀무가설을 상정함. 해당 유의도에 따라서 unit root의 존
재가 기각 될 수 있다.

(참고 : 실전 시계열 분석 책)

이해가 되지 않아 아래에서 다시 정리.

정상성(Stationarity)

회귀 분석을 할 때 오차의 정규성, 등분산성을 만족해야 회귀 분석 결과를 믿을 수 있는 것
처럼, 시계열 분석을 할 때 필수적으로 고려해야하는 가정임.

1. 정상성의 정의

과거와 현재와 미래의 모두 항상 안정적인, 일정한 분포를 가지는 시계열

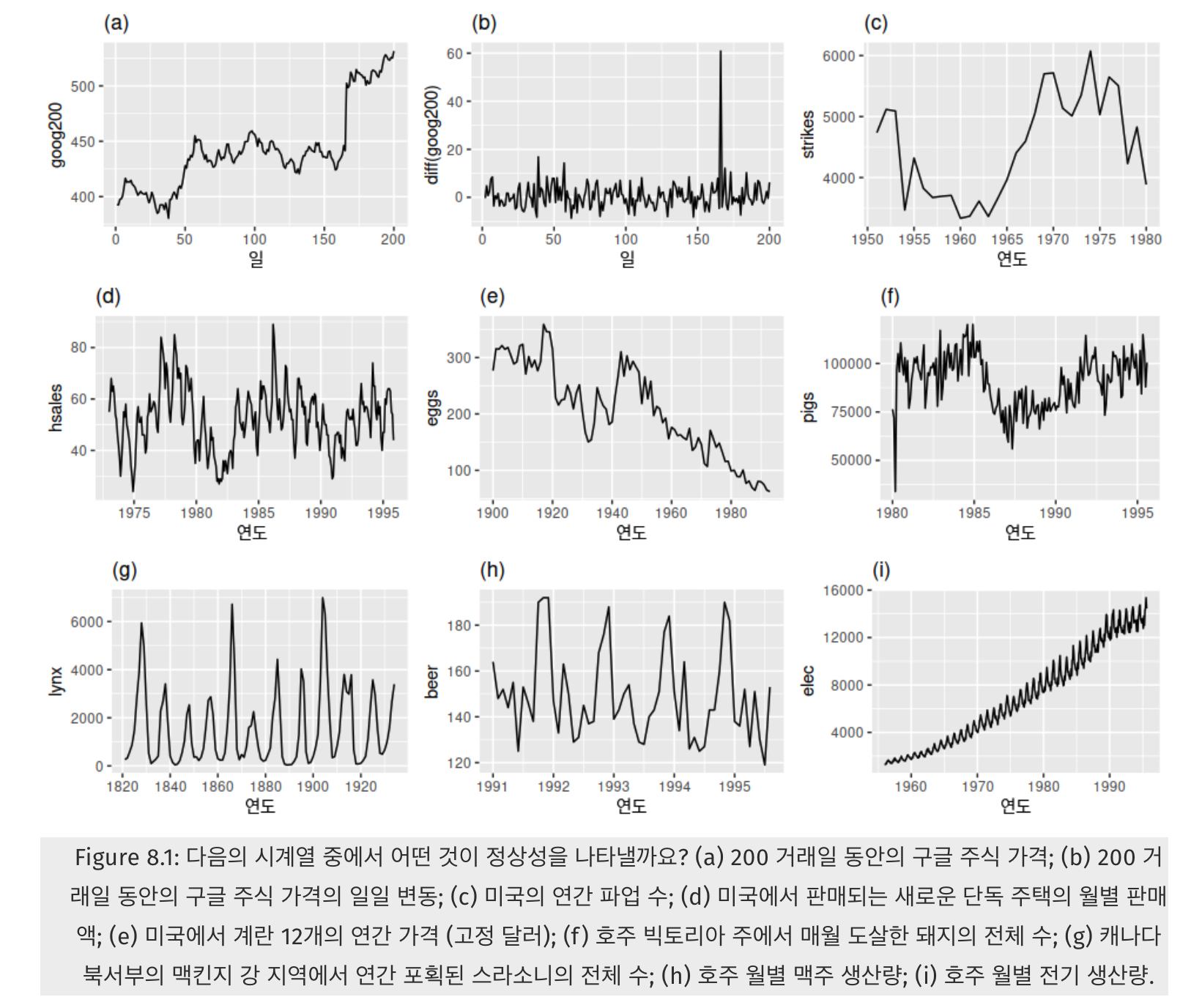
여기서 정상성을 가지는 시계열은 (b)와 (g) 밖에 없음.
정상성은 어떤 특정한 주기로 반복하는 계절성이나 위로 혹은 아래로 가는 트렌드가 없어야 하며,
분산도 커지면 안되는 것임. 즉, 시간에 무관하게 과거, 현재, 미래의 분포가 같아야한다는 의미.

엄밀히 정의하면,
"정상성이란 시계열의 평균과 분산이 일정하고, 특정한 트렌드가 존재하지 않는 성질을 의미함.

정상성에는 강한 정상성(strong stationarity)과 약한 정상성(weak stationarity)이 있음.

일반적으로 약한 정상성만 만족해도, 분석이 타당하다고 판단함.
약한 정상성을 수학적으로 더 엄밀하게 정의하면 다음의 세가지 조건을 만족해야함.

2. 정상성이 중요한 이유

시계열의 평균과 분산이 일정해야 시계열 값을 예측 할 수 있기 때문.
시계열 분석에서는 '우리가 구한 시계열 자료'가 어떤 시간에 따른 확률과정(stochastic process)에서 실현된 값이라고 봄.

여기서 $\bar{X}$는 우리가 얻은 $n$개의 데이터 (= 표본, samples) $X_1,X_2,\ldots,X_n$의 평균, 즉 표본 평균이고, $\mu$는 모 평균, $\sigma^2$은 모 분산에 해당하고, 이는 표본들의 평균이 일정한 평균과 분산을 가지는 정규분포를 따른다는 의미.

여기서 확장되어 확률 과정은 시간별로 표시된 확률 변수의 집합으로 정의가 됨. 즉, 각 시점 $t$에서의 값이 확률 분포 (예컨대, 위 예시처럼 각 시점에서의 값 (주가, 임금 등 우리가 관심있는 값) 이 정규분포를 따르는 것)를 따른다고 보고, 이를 종합적으로 고려했을 때 시간 $t \in [0,\infty]$에서의 값들이 어떤 확률 분포를 따를 때 확률 과정이라 부를 수 있음.

그런데, 우리가 얻은 데이터 (= 표본)에 대응되는 것이 우리가 얻은 시계열 자료이고, 이들은 일정한 평균과 분산을 가진 확률 과정 (stochastic process)을 따른다고 가정해야만 시계열 예측을 할 수 있음. 가령, 오늘의 주가가 3000원인데, 이 주가는 이상적인 천상의 주가 그래프에서 여러 개를 표본 선출하여 만든 수치들 (Ex. 2000원, 2500원, 5000원, .., 3000원)의 평균 값이라고 볼 수 있음.

만약 시간의 흐름에 따라서 이 확률 분포가 크게 변동한다면, 그 실현값들의 평균이나 분산 등 모멘트가 의미가 없기 때문에 적어도 이 평균과 분산이 우리가 다루고자 하는 확률 과정을 설명하기에 문제가 없도록 하기 위해 필요한 조건이 바로 정상성

결과적으로 정상성을 띄는 확률 과정을 그림으로 표현하면 아래와 같음.

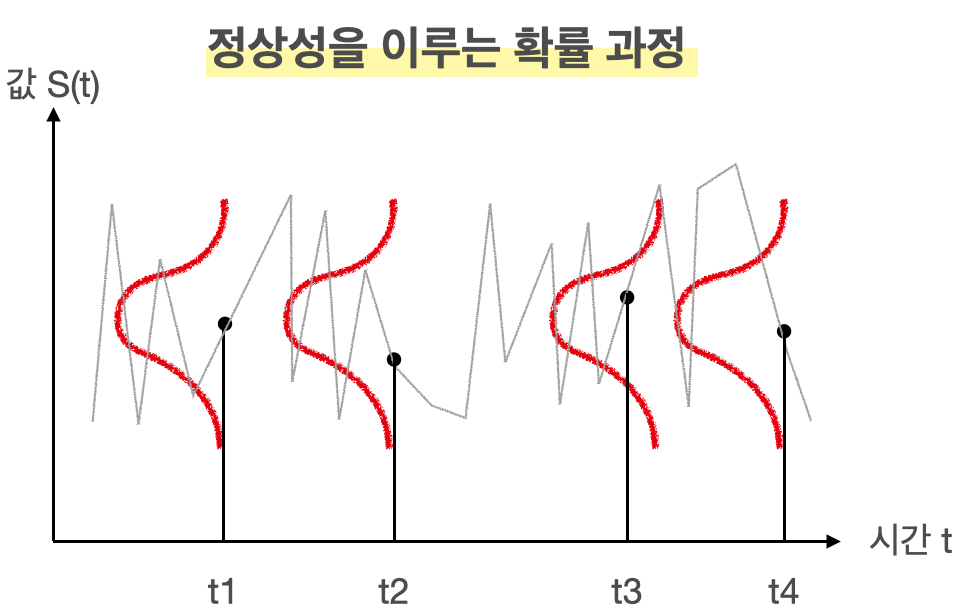
회색선이 시계열 자료라면, 빨간색 선처럼 각 시점에서 확률 분포를 가지고, 이들의 평균과 분사이 동일한 분포이므로 확률 과정이 정상성을 띈다 볼 수 있음.

상성을 만족시키기 위한 두 가지 방법

보통 시계열 자료는 정상성을 띠지 않는 자료가 많음. 생각해보면 주가도 시간에 따라 증가하는 모습을 보이고, 분산도 언제는 작았다가 언제는 크기도 하기 때문에 정상성을 띠지 않는게 대부분

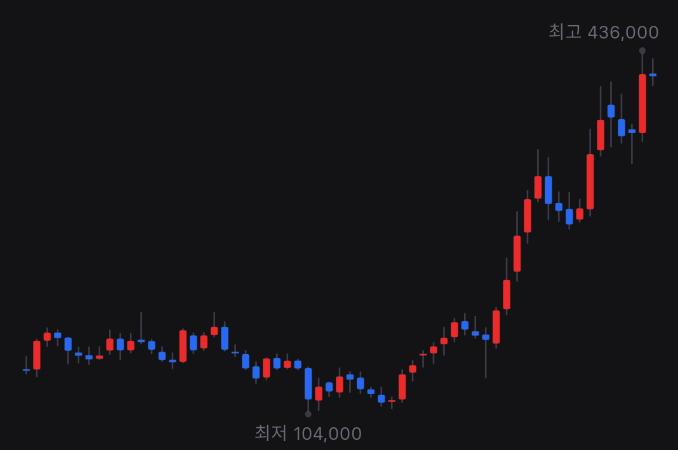
위 그림은 네이버 주가의 월봉 그래프로, 평균이 일정하지 않고 올라가는 추세를 보이고, 월마다 변하는 정도도 제각각인 것을 보아 분산도 다름을 유추할 수 있다. 즉, 정상성을 띠지 않는다.

이렇게 시계열 자료가 정상성을 띠지 않으면, AR, MA, ARIMA 등 전통적인 시계열 분석 방법들을 사용하기 어렵기 때문에 시계열 자료들에 어떤 변환을 취해 정상성을 띠도록 만들어야 합니다. 바로 차분 (Differencing)과 로그 변환입니다

차분(Differencing)

차분은 t시점과 t−1시점의 값의 차이를 구하는 것을 의미합니다.

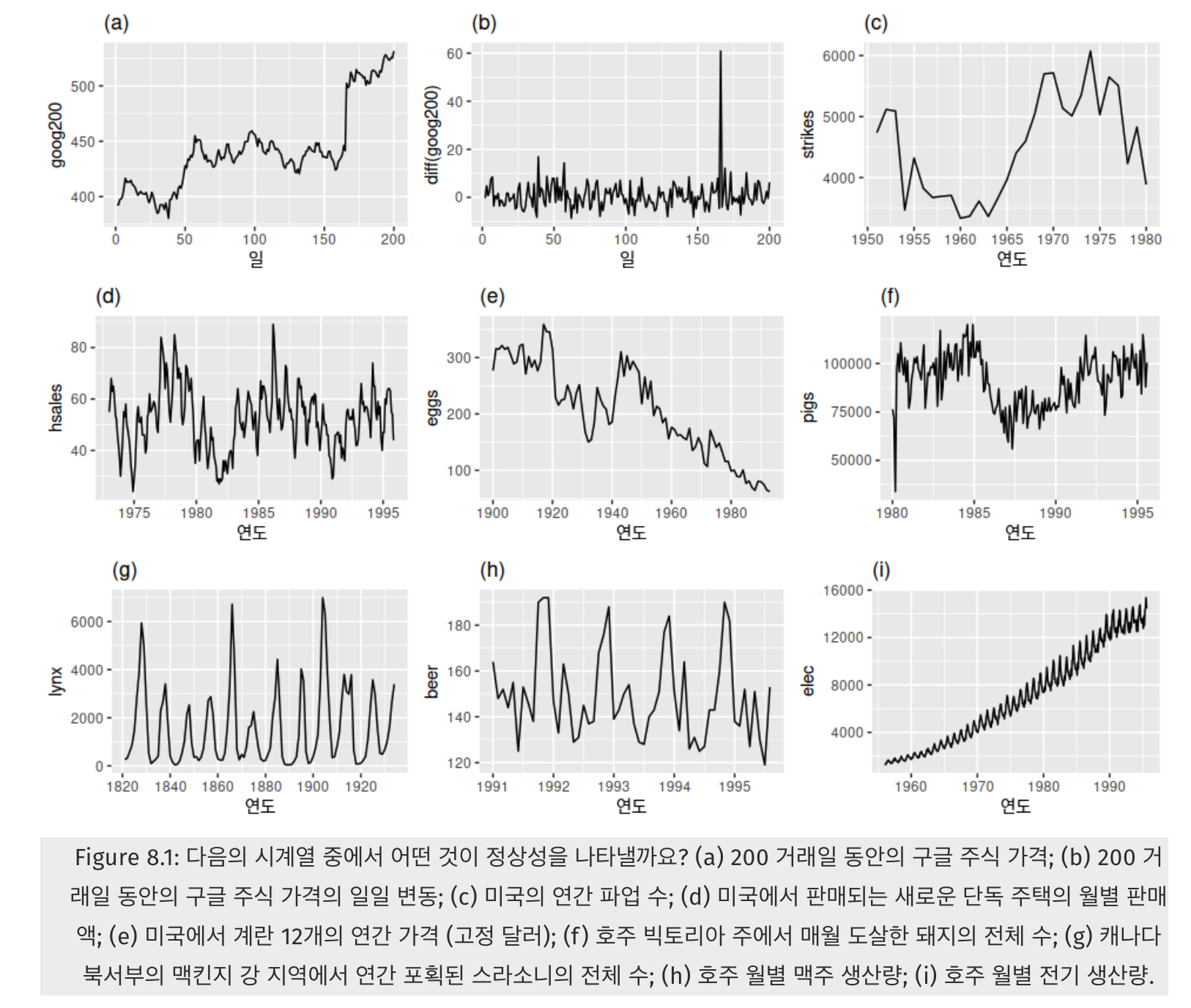
다시 위 그림에서 (a)의 구글의 주식 가격이 정상성을 나타내는 시계열이 아니었지만, (b)는 구글의 주식 가격의 일별 변화는 정상성을 나타냈음. 즉, 연이은 관측값의 차이를 계산하는 차분을 취하면, 그 차이값들의 평균은 일정하기 때문에 정상성을 띈다.

차분을 수식을 통해 정의하면 다음과 같음.

$\triangle y_t=y_t−y_{t−1}$
첫 번째 관측값에 대한 차분 $\triangle y_1$을 구할 수 없기 때문에, 차분값들은 $T−1$개의 값만 가지게 됨.

2차 차분

가끔 차분을 해도 시계열의 정상성이 만족되지 않는 경우도 있음. 그럴 경우, 정상성을 나타내는 시계열을 얻기 위해 다음과 같이 한 번 더 차분을 구하는 작업이 필요할 수도 있음.

$\triangle y_t−\triangle y_{t−1}=(y_t−y_{t−1})−(y_{t−1}−y_{t−2})=y_t−2y_{t−1}+y_{t−2}$
이 경우 2차 차분값은 T−2개의 값을 가지게 됨. 결국, 2차 차분은 원본 시계열 데이터의 “변화에서 나타나는 변화”를 모델링하게 되는 셈. 실제 상황에서는 2차 차분 이상으로 구하는 경우는 거의 일어나지 않음.

계절성 차분

계절성 차분은 관측치와, 같은 계절의 이전 관측값과의 차이를 말한다. 따라서 다음과 같이 정의가 됨.
$y_t−y_{t−m}$
여기서 $m$은 주기에 해당함. 즉 $m=12$이고 월별로 집계된 값이라면, 올해 1월의 값 - 작년 1월의 값, 올해 2월의 값 - 작년 2월의 값, … 이 됨.

로그 변환

로그 변환을 통해 정상성을 띠지 않는 시계열 자료의 분산을 줄일 수 있음.

정상성을 만족시키는 두 번째 방법으로 로그 변환을 고려할 수 있음. 말 그대로 값에 시계열 값에 로그를 취하면 됨.
$y_t→log(y_t)$
로그 변환은 특히 값의 변동 자체가 큰 경우 (= 분산이 큰 경우) 고려할 수 있는 방법이다. 또한, GDP와 같은 많은 경제 시게열 자료가 근사적으로 지수적인 성장을 나타내고 있는 경우가 많기 때문에 이런 시계열 자료에 로그를 취해 선형적인 값으로 바꿔주는 효과도 존재함.

그러나, 로그 변환을 통해 어떤 시계열 자료가 선형적인 추세를 보인다면 시간이 지남에 따라 평균이 일정하지 않고 증가한다는 뜻이기 때문에, 이 또한 정상성을 띠지 않는 문제가 있음. 그럼 뭐야? 라고 생각이 들겠지만 다음 장에서 그 해답을 찾을 수 있습니다.

로그 변환 + 차분(로그차분)

그래서 저희는 PPAP 전법이 필요하다고 한 블로그에서 비유하셨다.

• 로그 변환을 통해서 먼저 분산을 안정화시키고, 지수적인 값을 가지는 시계열을 선형적으로 바꿔준 다음,
• 그 변환된 시계열 값에 차분을 취해 정상성을 만족시키도록 만드는 것

시간에 따라 어떤 시계열이 선형적으로 증가한다는 뜻은 즉, 그 시간에 따른 증가분 (차분)이 일정하다는 것이기 때문에, 로그 변환된 시계열에 차분까지 해주면 정상성을 만족시킬 수 있는 것임.

더 놀라운 것은 로그의 차분값이 증가율의 근사값이라는 것이 알려져 있습니다. 저희가 PPAP 전법을 통해 로그의 차분값을 다음과 같이 정의한다면,
$\triangle \log(y_t)=\log{y_t}−\log{y_{t−1}}$
이 값을 $y_{t−1}$에서 $y_t$로의 증가율로 근사할 수 있습니다.

$Δlog(y_t)=\log{y_t}−\log{y_{t−1}}$ ≃ ${yt−y{t−1}}\over{y_{t−1

왜 놀랍냐면, 해석 상 이점이 있기 때문입니다. 가령 “GDP의 로그의 차분값이 AR (1)과정을 따릅니다”라는 말보다 “GDP의 증가율이 AR(1) 과정을 따릅니다”가 직관적으로 잘 와닿기 때문.

그렇다면 이 PPAP전법(?)ㅋㅋ 이 잘 통하지 않는 경우에는 로그 차분값에 또 차분(즉, 2차 차분)을 시행하면 됨.

정상 검증을 위한 두가지 방법

이렇게 차분 또는 로그 변환을 통해 시계열을 “안정화”시켜줬을 때 실제로 그 변환된 시계열이 정상성을 만족하는지 검증하는 과정이 한데, 크게 1)그래프로 직관적으로 파악하는 방법과 2)통계적인 검정 방법을 이용하여 정상성을 검증가능함.

그래프로 정상성 파악하기

그래프 상 추세가 없이 일정한 폭으로 상승과 하락을 반복한다면 정상성을 띠는 그래프라 추측할 수 있다 또한, ACF가 허용 범위 안에 존재한다면 정상성을 띤다 말할 수 있다.

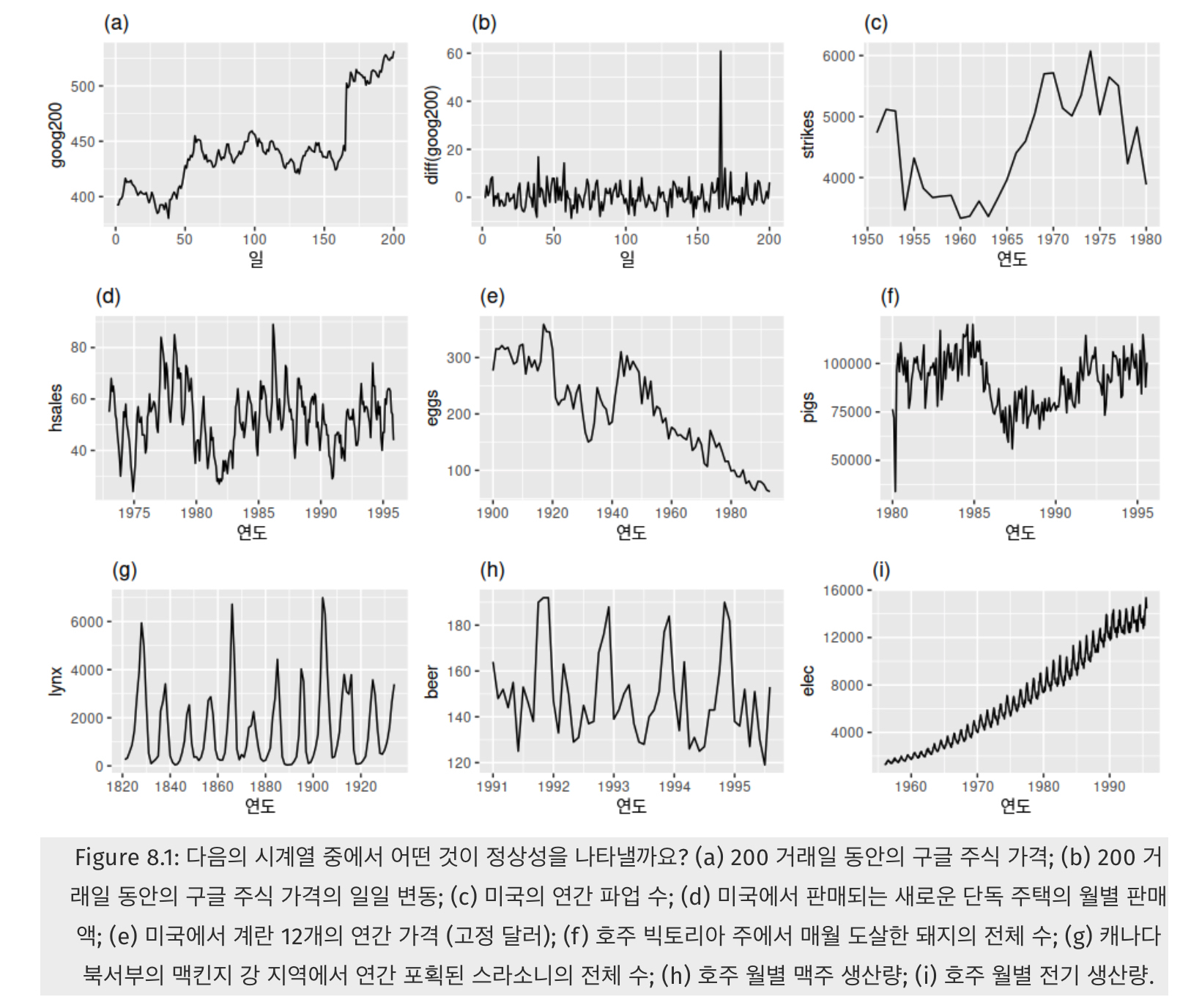
여기서 정상성을 가지는 시계열은 (b)와 (g) 뿐임.

이처럼 시계열의 모습만 보고도 직관적으로 정상성을 띠는지 확인할 수 있다 정상성의 정의에 따라서,

• 그래프에 지속적인 상승 또는 하락 추세가 없어야 하고
• 과거의 변동폭과 현재의 변동폭이 같아야 하며
• 계절성도 없어야 함.

또한, 이런 정상성을 가진 시계열은 평균으로 회귀하려는 특징 (Mean reverting)을 가지고 있음. 즉, 어떤 시점에서 평균을 크게 벗어났는데 조만간 다시 평균으로 돌아가려는 성향을 가지고 있다면, 정상성을 가진다 추측해볼 수 있음.

이보다 더 직관적인 방법은 자기 상관 함수 (ACF; Auto Correlation Function) 을 이용하는 것입니다. 자기 상관 함수는 전혀 새로운 개념은 아니고, 일반적인 상관 계수를 구하는 공식에서 X와 Y간의 상관 관계를 구하는 대신, 시계열 자료인 X 자체의 상관 관계를 구하기 위해 고안된 것임. 즉, 시계열 자료에서 t 시점의 값과 그보다 k시점 앞선 t−k 시점 간의 상관 계수를
$r_k$라 할 때, 다음과 같이 자기 상관 함수가 정의된다.

$r_k$ = $\sum_{t=k+1}^T (y_t - \bar y)(y_{t-k} - \bar y) \over \sum_t^T (y_t - \bar y)^2$
여기서 $T$는 시계열 데이터의 행 수를 의미함.

ACF를 그렸을 때 어떻게 나와야 정상성이 보이는 걸까? 즉, 어떤 ACF가 정상성을 띄는 그래프일지 골라보자.

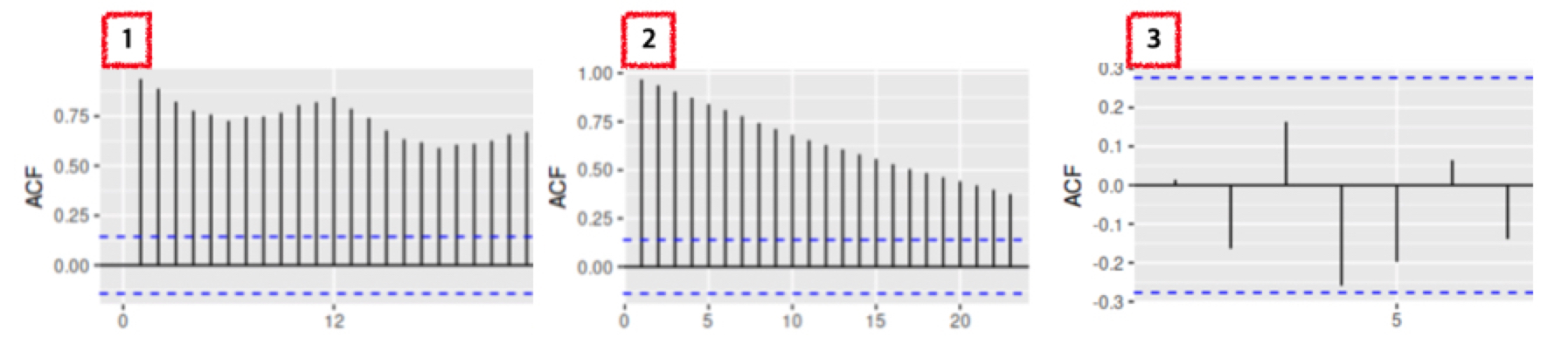
정답은 3번 그래프이다. 3번 그래프와 1, 2번 그래프를 비교했을 때 가장 큰 차이점은 “파란색 점선 안에 값이 들어왔는지“이다.

ACF 그래프에서 가로축은 시차 (lag), 세로축은 ACF의 값이다. 예를 들어, 4에 찍힌 값은 yt와 네 시점 앞인 yt−4 간의 ACF를 의미한. 이 때 1번과 2번은 시차가 뒤로 갈수록 ACF 값이 감소하고 있지만, 확연하게 줄어들지 않는다. 이것은 오늘의 데이터가 어제의 데이터에 가장 크게 의존하고, 시간이 지날수록 오늘과 먼 과거의 데이터 간의 자기 상관은 감소함을 의미한다.

이에 비해 정상성을 띠는 데이터는 파란색 점선, 즉 신뢰 구간 안에 자기 상관이 존재한다. 이럴 경우, 데이터가 정상성을 띤다고 할 수 있다. 즉, 어제의 데이터와 오늘의 데이터 간에 상관 관계는 당연히 있겠지만, 허용 범위 (파란색 점선) 안에 들어온다는 것을 의미한다.

가설 검정으로 정상성 파악하기

귀무 가설을 기각해야(p-value가 작아야) 정상성을 띈다.

정상성을 파악하는 두 번째 방법은 가설 검정입니다. 바로 단위근 검정 (Unit Root Test) 인데, 이 검정에는 여러 학자들이 고안하여 검정 방법이 아래와 같이 존재합니다.

• KPSS 검정
• Dicky-Fuller 검정
• ADF 검정 (Augmented Dicky-Fuller Test)
  설명의 편의성을 위해, AR(1)모형에서의 Dicky-Fuller Test에 대해 알아보겠다.

AR(1) 모형은 아직 설명하지 못했지만 현 시점의 값이 한 시점 앞의 시점 (lag = 1)의 값에 의존하는 모형으로, 다음과 같이 쓸 수 있다.

$y_t=β_0+β_1y_{t−1}+e_t$
여기서의 귀무 가설과 대립 가설은 $H_0=β_1=1$ vs. $H_1:β_1<1$로 정의가 되는데 귀무 가설을 만족한다면 $β_1=1$이고, 이 때의 모형은 $y_t=β_0+y_{t−1}+e_t$가 된다.

이런 모형이 어떻게 생겼는지 아래 두 모형으로 간단하게 시뮬레이션을 해보자.

모형 1: $β_0=3,β_=1 → y_t=3+y_{t−1}+e_t$
모형 2: $β_0=3,β_1=0.1→z_t=3+0.1z_{t−1}+e_t$

import numpy as np
import matplotlib.pyplot as plt
init = np.random.normal(size=1, loc = 3)
e = np.random.normal(size=1000, scale = 3)

y = np.zeros(1000)
z = np.zeros(1000)
y[0] = init
z[0] = init

for t in range(1,1000):
    y[t] = 3 + 1 * y[t-1] + e[t] # beta1 = 1 단위근 모형
    z[t] = 3 + 0.1*z[t-1] + e[t] # beta1 = 0.1

fig,ax = plt.subplots(1,2)
ax[0].plot(y)
ax[0].set_title("Non-Stationary")
ax[1].plot(z)
ax[1].set_title("Stationary")
plt.show()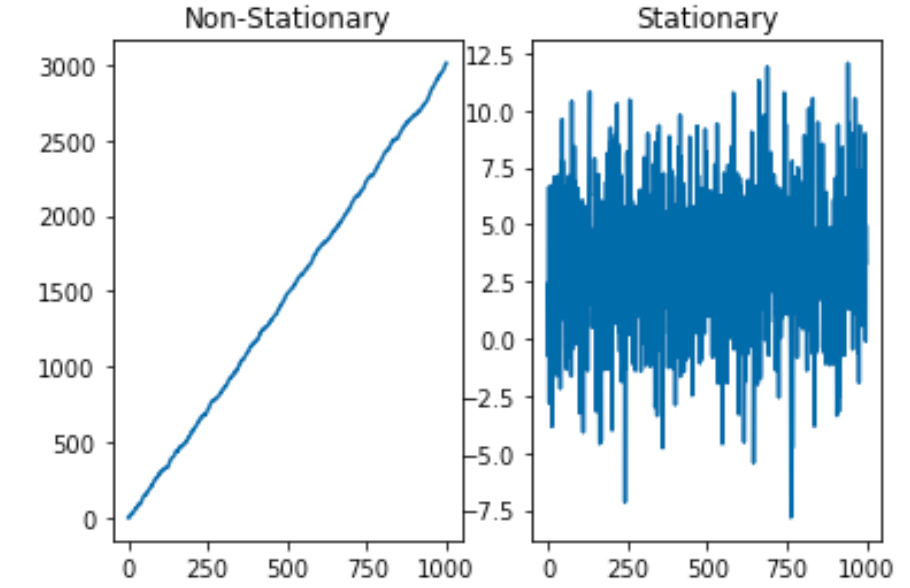    

그래프로 판단해봤을 때, $y_t$는 아주 강력한 상승 추세를 가지기 때문에 정상성을 띠지 않지만, $z_t$는 정상성을 띠는 듯하다.

이처럼 $β_1=1$이면 단위근을 가졌다고 하고, 이 단위근을 가진 AR 모형 $y_t$ 은 정상성을 띠지 않는다. 따라서 귀무 가설 $β_1=1$을 기각해야 정상성을 띤다 말할 수 있다.

위에 책에서도 이해를 못했던 단위근이 또 나왔다. 단위근이란....???

AR(p) 모형 (시차 = p까지 설명이 되는 모형)이 정상성을 띠기 위한 조건은 특성 방정식의 모든 근의 절대값이 1보다 커야 한다는 것. 특성 방정식은 다음과 같이 쓸 수 있음.

$1−β_1B−β_2B^2−⋯−β_pB^p=0$

여기서 B는 후방 이동 (backshift) 연산자로, 시계열의 시차를 다룰 때 쓰는 표기법. 아래와 같음

$By_t = y_{t−1}$
$B^2y_t=y_{t−2}$
⋮

만약 이 특성방정식의 근이 1인 것을 가지고 있다면 이 때 단위근을 가지고 있다고 말한다. $y_t=y_{t−1}+e_t$ 모형으로 특성 방정식과 그 근을 보자. 이 모형은 $β_1=1$인 AR(1)모형으로 확률 보행 모형 (random walk model) 이라 부른다. 이 모형에 후방 이동 연산자를 적용하고, 에러 $e_t$에 대해 식을 정리한다면 특성 방정식의 해를 구할 수 있음.

$y_t=By_t+e_t$
$e_t = y_t−By_t$
$e_t=(1−B)y_t$

여기서의 특성 방정식은 $(1−B)=0$이 되어 해가 B=1로 계산이 된다. 그래서 이 모형은 단위근을 갖게 되고, 정상성을 가지지 않는 대표적인 모형임.