자기 회귀 모델(AR : Autoregressive Model)
과거의 값이 현재의 값에 영향을 줄 때 사용하는 모델
자기 회귀 (AR; Autoregressive) 모델은 과거가 미래를 예측한다는 직관적인 사실에 의존합니다. 차수가 p인 AR(p) 자기 회귀 모형은 다음과 같이 쓸 수 있습니다.
여기서 는 백색잡음 (white noise)자기 상관이 없는 시계열입니다. 백색 잡음은
평균이 0이고
분산은 σ2로 일정해야하고
서로 다른 시점에서의 공분산도 0인 시계열
을 의미합니다. 정의에서 알 수 있듯이 백색잡음은 정상성을 띱니다. AR 식이 의미하는 바는 t시점의 값을 최대 t−p 시점 이전의 값까지 포함하여 회귀식을 완성해야 잔차 ϵt의 값이 과거의 잔차들의 값에 의존하지 않음을 의미합니다.
백색 잡음 / 확률 보행 / 표류가 있는 확률 보행 / 정상성을 만족하는 모형
이를 단순화해서 가 그 직전 시점인 에만 의존하는 즉, 차수가 1인 AR(1) 모형을 살펴봅시다.
여기서 ϕ1과 c의 값에 따라서 AR(1)모형은 다양한 이름으로 불립니다.
백색 잡음 (White noise model)
과거의 값과 현재의 값의 상관관계가 없는, 단순한 Shock 형태
일 때 는 백색잡음입니다. 백색잡음 모형은 위에서 설명했듯이, 과거의 값으로 현재의 값을 예측할 수 없는 랜덤한 상태를 의미합니다
확률 보행 (Random walk model)
, 현재의 값을 예측할 수 있는 가장 좋은 값은 어제의 값
이면 로, 이 모형은 확률보행 (Random walk) 모형입니다. 이 모형은 정상성을 띠지 않습니다. 이 모형의 의미는 오늘 시계열 값 은 어제의 시계열 값 + 예측할 수 없는 변화량 으로 설명된다는 것을 의미합니다. 결과적으로, 현재의 값을 예측할 때 가장 좋은 값은 어제의 값이다라는 뜻이죠.
이 모형은 확률론적 추세 (Stochastic trend)가 존재하는 가장 단순한 모형입니다.
표류가 있는 확률 보행 (Random walk model with a drift)
, 시간이 지남에 따라 평균적으로 값이 증가하거나 감소하는 형태
이면 로, 여기서 상수 c를 표류 (drift)라 합니다. 그래서 이 모형은 표류가 있는 확률 보행 (Random walk with a drift) 모형입니다.
이 모형의 특징은 모형을 아래와 같이 바꿔쓸 수 있다는 것인데요.
을 시계열의 초기값이고, 부터 순차적으로 적용하여 대입한다고 했을 때,
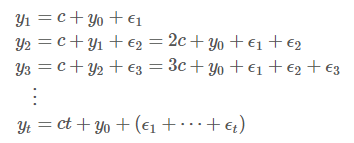
이렇게 전개가 됩니다.
이 모형은 확정적인 추세 (Deterministic trend) 를 가지고 있고, c>0이라면 시간에 따라 평균적으로 증가하는 모습을 보입니다.
−1<ϕ1<1인 정상성을 만족하는 모형
−1<ϕ1<1인 , 정상성 (Stationarity)을 띠는 AR(1) 모형
−1<ϕ1<1이면 정상성 (Stationarity)을 띠는 AR (1)모형입니다.
확률 보행 모델이 정상성을 띠지 않는 이유
확률 보행 모델은 시간이 지남에 따라 분산이 커지기 때문에 정상성을 만족하지 않습니다.
자, 그럼 눈치 상 AR(1) 모형에서 네 가지 경우를 말씀드렸는데, 여기서 정상성을 띠는 모형은 첫 번째 소개드린 백색 잡음 모형 (White noise model)과 계수가 인 모형뿐이고 확률 보행 모델은 정상성을 띄지 않습니다. AR(1)의 모형에서 정상성을 띌 조건은 이고, 확률 보행 모형의 값은 1이기 때문에 그렇습니다.
그런데 왜 정상성을 띠지 않을까요? 이 확률보행 모형은 시간이 지남에 따라 분산이 증가하여 의 분포가 시간에 따라 변하기 때문입니다. 이를 수식을 통해 증명하고자 합니다. 다음과 같은 확률보행 모형을 가정합니다.
초기값 이라 했을 때 다음과 같이 시계열을 풀어쓸 수 있습니다.
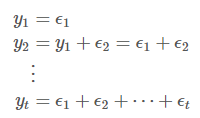
이 때 의 분산을 구하면 잔차들의 분산의 합으로 계산되고 잔차의 분산은 으로 가정했으므로 이 됩니다. 아래와 같이 말이죠!
참고로, 는 백색잡음으로, i.i.d한 성질을 가지기 때문에 로 쓸 수 있습니다. 그리하여 의 분산은 t에 의존하게 되어 t가 증가함에 따라 (시간이 지남에 따라) 분산이 커지게 됩니다. 따라서 정상성의 정의에 따라서 분산이 유한하지 않아 정상성을 띠지 않게 됩니다.
AR (1) 정상성을 만족할 조건 증명하기
이렇게 정상성이 없는 시계열에 그대로 AR 모형을 적용하게 되면 터무니없는 예측치를 내기 때문에 시계열 모형이 정상성을 띠도록 차분 / 로그 변환을 하여 모형을 적용해야 합니다. 정상성을 띠어야 하는 이유는 정상성을 띠어야 시계열의 과거, 현재, 미래의 분포가 같기 때문에 미래의 값을 예측할 수 있기 때문이죠.
그럼 왜 AR(1)에서 정상성을 띨 조건이 일까요?
AR(1)모형이 정상성을 띤다고 가정하고,
계수 에 어떤 제약조건이 필요한지 보겠습니다.
우선 정상성의 정의로부터 임의의 시점인 t에서의 기대값이 모두 같아야 합니다.
그리고 AR모형의 정의에 따르면 의 기대값은 0이여야 합니다. 따라서
가 되고, 를 양변에 대입하면 아래와 같은 결과를 냅니다.
이를 이라는 관계를 이용하여 AR(1) 모형에 대입하면
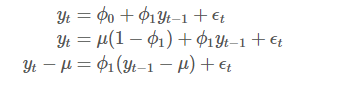
위와 같이 시계열 값에서 평균을 뺀 값에 대한 식으로 나타낼 수 있습니다. 위 식에서 분산을 구하고, 임의의 시점인 t에서 분산이 같아야한다는 정상성의 정의를 이용하면
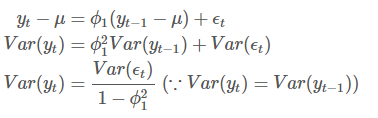
과 같은 결과를 얻습니다. 또한, 분산은 무조건 0보다 크거나 같아야 하므로 이 반드시 1보다 작아야 합니다. 이는 정상과정에서 의 범위가 이 되어야한다는 의미입니다.
이동 평균 모델 (MA; Moving Average Model)
과거의 충격 (Shock)이 현재의 값에 영향을 줄 때 쓸 수 있는 모형
Shock이라는게 무엇일까요?
이동 평균 모델은 과거의 시계열 값을 이용하는 대신에 과거의 오차를 이용해 회귀식을 세웁니다. 차수가 인 MA(q) 모델은 다음과 같이 정의됩니다.
예를들어,
일별 수영장에 입장하는 사람수에 대한 모델링을 한다 가정해봅시다. 사람들은 보통 수영장을 갈 때 어떤 것을 많이 신경쓸까요? 수영장 가는 날 “비가 내리는지” 신경을 많이 쓸 것입니다. 강수 여부를 예측하기 어렵고 i.i.d를 따른다 가정했을 때, 비가 많이 오면 “weather shock”(굳이 한국말로 번역하면 날씨 충격)은 오늘 뿐 아니라 내일, 모레의 수영장에 입장하는 사람 수에 영향을 줄 것입니다. 사람들은 보통 오늘 비가 오면 기상 예보를 보면서 내일과 모레의 날씨를 가늠하곤 하죠. 또한, 비가 온다고 예상이 되면 굳이 그 날에 수영장을 가지 않을 것입니다. 엄청난 놀이기구 마니아면 몰라도 말이죠!
결과적으로, MA 모형은 “과거의 충격이 현재의 결과에 영향을 주는 경우” 사용할 수 있고, 이런 식으로 모델링이 될 것입니다:
여기서 날씨는 오차 내지는 충격 (Shock)에 해당하며, 예측하기 어려운 변수로 가정됩니다.
MA 모형이 항상 정상성을 만족하는 이유
MA 정의 상 평균과 분산이 일정하므로 정상성을 만족합니다.
신기하지 않나요? AR(1) 모형에선 정상성을 띠기 위해 조건이 필요했는데, 정의상 MA 모델은 어떠한 모수에 제약이 없어도 약한 정상성을 띱니다.
자, 그럼 또 모형을 단순화하여 MA(1) 과정에서 왜 정상성을 띠는지 알아봅시다.
약한 정상성을 띨 조건은 평균과 분산이 유한하고, 둘 다 시간에 따라서 바뀌지 않아야 합니다. MA 모델은 정의상 오차 ϵt가 평균을 0으로 하는 독립 항등 분포 (ϵt∼N(0,σ2))이기 때문에 다음과 같이 평균과 분산을 구할 수 있습니다.
-
평균 = c로 상수
-
분산도 상수
그렇기 때문에 MA 모델은 약한 정상성을 띤다고 할 수 있습니다.
ARIMA 모델 (Autoregressive Integrated Moving-Average Model)
주식처럼 충격(Shock)에도 민감하고, 과거의 값에도 영향을 받는 총체적 난국일 때 쓰는 모형
드디어 대망의 ARIMA 모델이 왔습니다!
ARIMA 모델은 AR 모형 부분도 있고, MA 부분도 있는데, 차분까지 한 PPAP(앞의 글에서 언급)의 진화 버전 PPPAP의 형태라 할 수 있습니다. ARIMA (p,d,q) 모델은 다음과 같이 정의됩니다.
여기서 는 차분을 구한 시계열입니다. (한 번 이상 차분을 구한 것일 수 있습니다)
또한 식을 자세히 보면 차까지 AR처럼 과거의 값들이 들어가있고, 차까지 MA처럼 가 전개되어있습니다. 따라서, 모수 는 다음과 같은 의미를 같습니다.
- : AR 부분의 차수
- : 차분의 정도
- : MA 부분의 차수
즉 ARIMA (1,0,0)이면 AR(1)모형과 같고, ARIMA(0,0,1)이면 MA(1) 모형이 됩니다.
이를 일반화하여 ARIMA에 특별한 경우를 정리하면 다음과 같습니다.
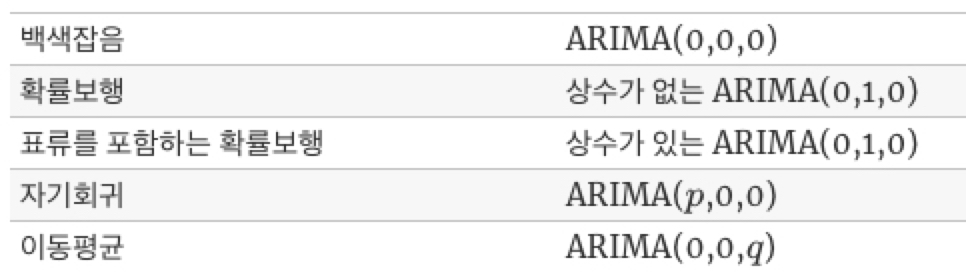
참고로 ARIMA에서 “I”가 빠지면 ARMA(p,q)과정인데 이는 차분만 안했을 뿐 AR 과 MA 과정이 합쳐진 모형입니다.
이 글은
https://assaeunji.github.io/statistics/2021-08-23-arima/ 를 가지고왔습니다. 완전 정리 잘해놓으셨더라구요..!! 강추
