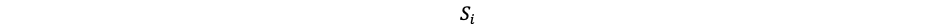[알고리즘] Knapsack Problem

이인석·2021년 12월 27일

12865 C Knapsack ProblemSolving 알고리즘

Algorithm

목록 보기

1/2

정의

Knapsack Problem은 일정 무게를 담을 수 있는 배낭 안에 담을 수 있는 물건의 총량을 최적화 하는 문제이다. 배낭의 크기, 물건의 개수, 각 물건의 무게와 가치가 주어질 때, 배낭에 넣을 수 있는 물건들의 가치가 최대가 되게 하는 조합을 찾는 문제이다.
Knapsack Problem은 크게 0-1 Knapsack Problem과 Fractional Knapsack Problem으로 나뉜다.

Knapsack Problem의 예제는 백준 문제 12865번. 평범한 배낭 문제를 풀었다.

0-1 Knapsack Problem

물건을 쪼개 배낭에 넣을 수 없을 때, 각 물건을 배낭에 넣을 지 말지 결정하는 문제.
Dynamic Programming으로 문제를 해결할 수 있다.

접근 방식

Data Structure

물건의 무게, 가치를 저장할 Structure

물건의 개수 * 가방의 무게만큼의 데이터를 저장할 수 있는 2-D Array

Concept

물건을 최적으로 조합해야 하므로, 각 배낭의 무게에서 가질 수 있는 최고의 가치를 저장해두고, 다음 물건을 탐색할 때 이전 물건까지의 결과값을 참고하는 방식으로 해결할 수 있다.

Case1: 물건의 무게가 남아있는 배낭의 무게보다 큰 경우
-> 물건이 들어갈 수 없기 때문에, 이전 물건의 현재 남은 배낭 무게에서의 가치와, 현재 물건의 가치와 현재 물건이 들어갈 자리를 남긴 상태에서의 이전 물건의 가치 합과 비교한다.

Case2: 물건의 무게가 남아있는 배낭의 무게보다 작은 경우
-> 물건이 들어갈 수 있기 때문에 이전 물건을 탐색할 때 같은 무게에 현재 물건의 가치를 더한다.

일반화

위 컨셉을 일반화 하면 다음과 같다.

Notation

Fomula

위와 같은 일반식으로 생성한 2-D array의 최대값을 구한다.

코드구현(C++)

#include <iostream>
#include <stdlib.h>

using namespace std;

struct thing{
    int weight;
    int value;
};

int n, k;
thing* things;

int main(){
    cin >> n >> k;

    things = new thing[n];
    int ** mat;
    mat = (int **) malloc(sizeof(int *) * (n));    

    for(int i = 0; i < n; i++){
        cin >> things[i].weight >> things[i].value;
        mat[i] = new int[k+1];
    }

    int max_val = 0;

    for(int i = 0; i <= k; i++){
        if(things[0].weight > i) mat[0][i] = 0;
        else mat[0][i] = things[0].value;
    }

    max_val = mat[0][k];

    for(int i = 1; i < n; i++){
        for(int j = 0; j <= k; j++){
            if(j < things[i].weight) mat[i][j] = mat[i-1][j];
            else{
                int val1 = things[i].value + mat[i-1][j-things[i].weight];
                int val2 = mat[i-1][j];

                mat[i][j] = val1 > val2? val1 : val2;

                if(mat[i][j] > max_val) max_val = mat[i][j];
            }
        }
    }

    cout << max_val << endl;
}

Factional Knapsack Problem

물건을 쪼개 배낭에 넣을 수 있을 때, 배낭 안에 들어갈 수 있는 최대 가치를 구하는 문제.
Greedy Algorithm으로 문제를 해결할 수 있다.

접근 방식

물건을 쪼갤 수 있기 때문에, 각 물건의 가치와 무게의 비율을 계산한다.

계산한 물건의 단위 무게당 가치 비율이 높은 순서로 정렬한다.

물건을 차례대로 가방에 넣고, 가방에 전부 넣지 못하는 마지막 물건을 쪼개 넣을 수 있는 만큼만 넣어준다.

코드 구현(C++)

#include <iostream>
#include <algorithm>

using namespace std;

struct thing{
    int weight;
    int value;
    double value_ratio;
};

bool cmp(thing t1, thing t2){
    return t1.value_ratio > t2.value_ratio;
}

int n, k;
thing* things;

int main(){
    cin >> n >> k;

    things = new thing[n];

    for(int i = 0; i < n; i++){
        cin >> things[i].weight >> things[i].value;
        things[i].value_ratio = (double) things[i].value / things[i].weight;
    }

    sort(things, things + n, cmp);

    double max_val = 0;

    int idx = 0;
    while(1){
        if(things[idx].weight > k){
            max_val += things[idx].value_ratio * k;
            break;
        }
        else{
            max_val += things[idx].value;
            k -= things[idx].weight;
        }
        idx++;
        if(k == 0 || idx == n) break;
    }

    cout << max_val << endl;
}