[통계] 선형회귀 - (2) 실습

전도운·2024년 8월 15일

python 통계

seaborn에서 제공하는 diamonds 실습 데이터를 이용해서 선형회귀분석의 기본 가정을 확인하고 실제 회귀식을 적합해본다.

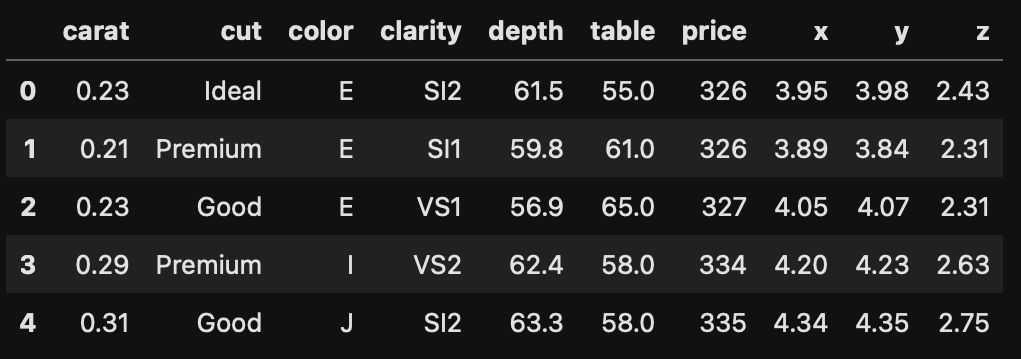
💎 다이아몬드 데이터

Format: A data frame with 53940 rows and 10 variables:
price: price in US dollars ($326--$18,823)
carat: weight of the diamond (0.2--5.01)
cut: quality of the cut (Fair, Good, Very Good, Premium, Ideal)
color: diamond colour, from D (best) to J (worst)
clarity: a measurement of how clear the diamond is (I1 (worst), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (best))
x: length in mm (0--10.74)
y: width in mm (0--58.9)
z: depth in mm (0--31.8)
depth: total depth percentage = z / mean(x, y) = 2 * z / (x + y) (43--79)
table: width of top of diamond relative to widest point (43--95)

1. 분석 목표 설정

다이아몬드의 가격(price)에 영향을 미치는 요인을 살펴본다.
선형회귀분석을 적용하고 회귀계수의 절대값 크기로 영향도를 판단한다.

2. 탐색적 데이터분석(EDA)

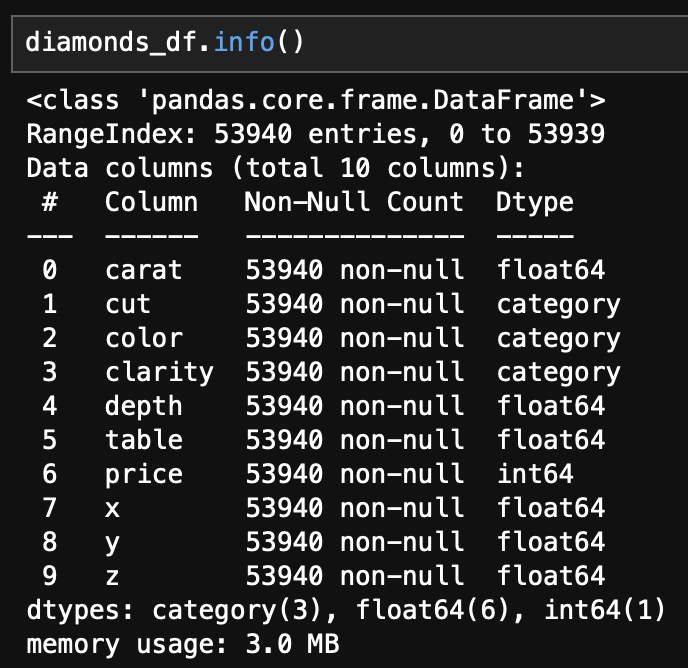
데이터 기본정보
- 행이 53940개에 달하는 꽤 큰 데이터이다.
- 결측치는 확인되지 않는다.
- float형 변수 6개, category형 변수 3개, int형 변수 1개
기초통계
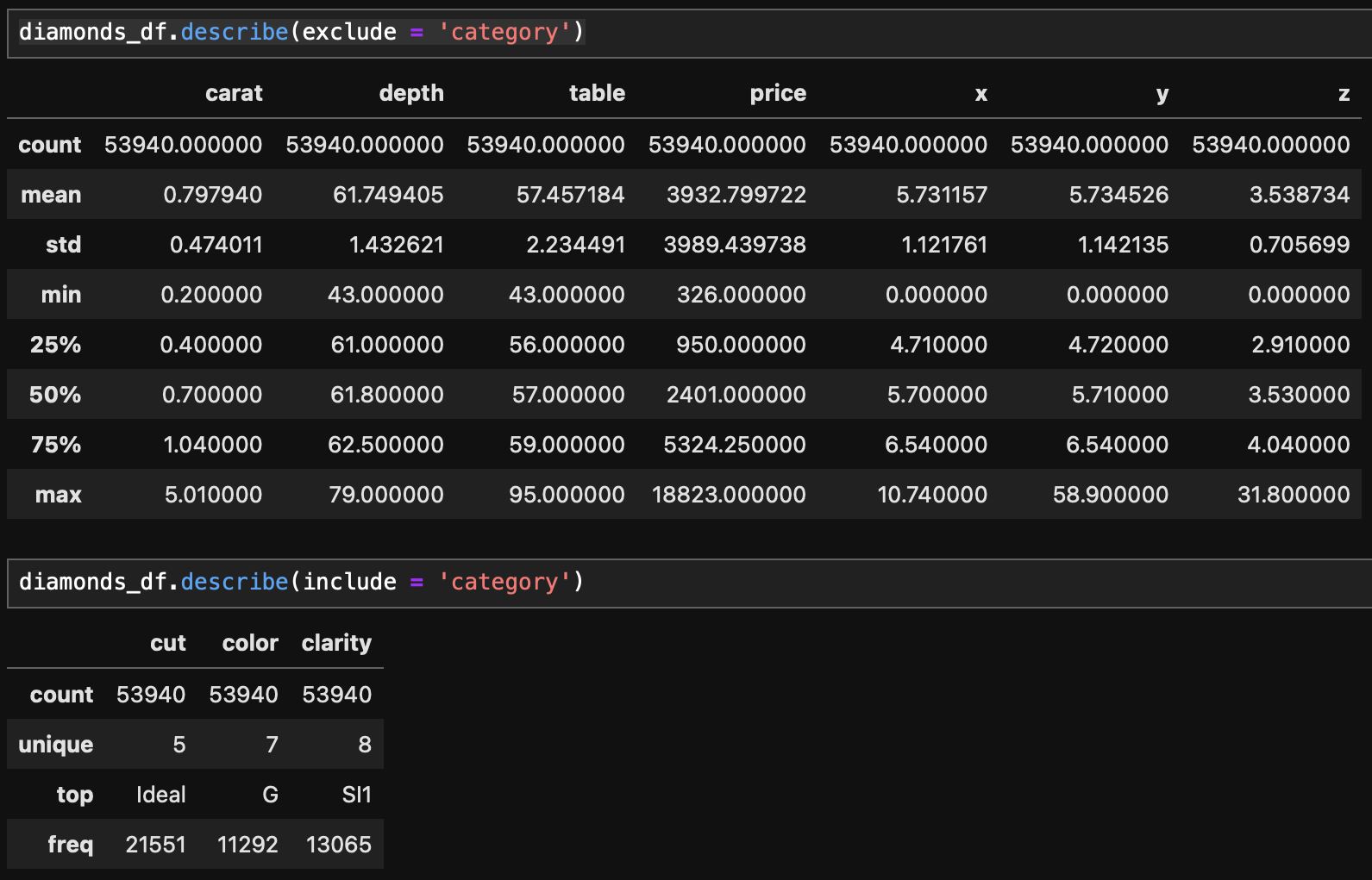
- price, x, y, z변수의 자료 분포가 큰 것이 확인된다.
시각화
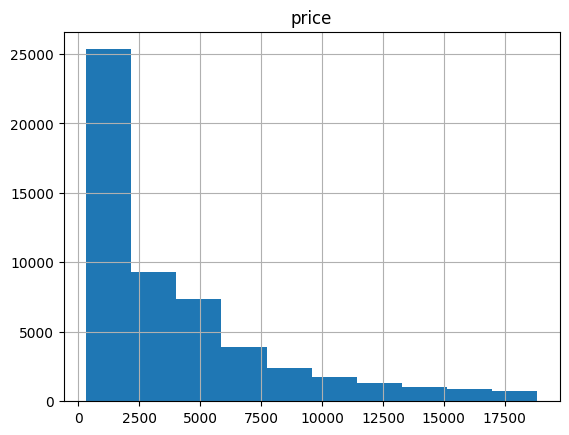
- price 변수의 데이터 분포가 넓으므로 price와 price 외 변수로 나눠서 시각화
- 종속변수로 사용할 price가 오른쪽으로 긴 꼬리 분포를 보이고 있어 평균과 정규성을 이용한 선형회귀에는 적합하지 않을 것으로 예상됨
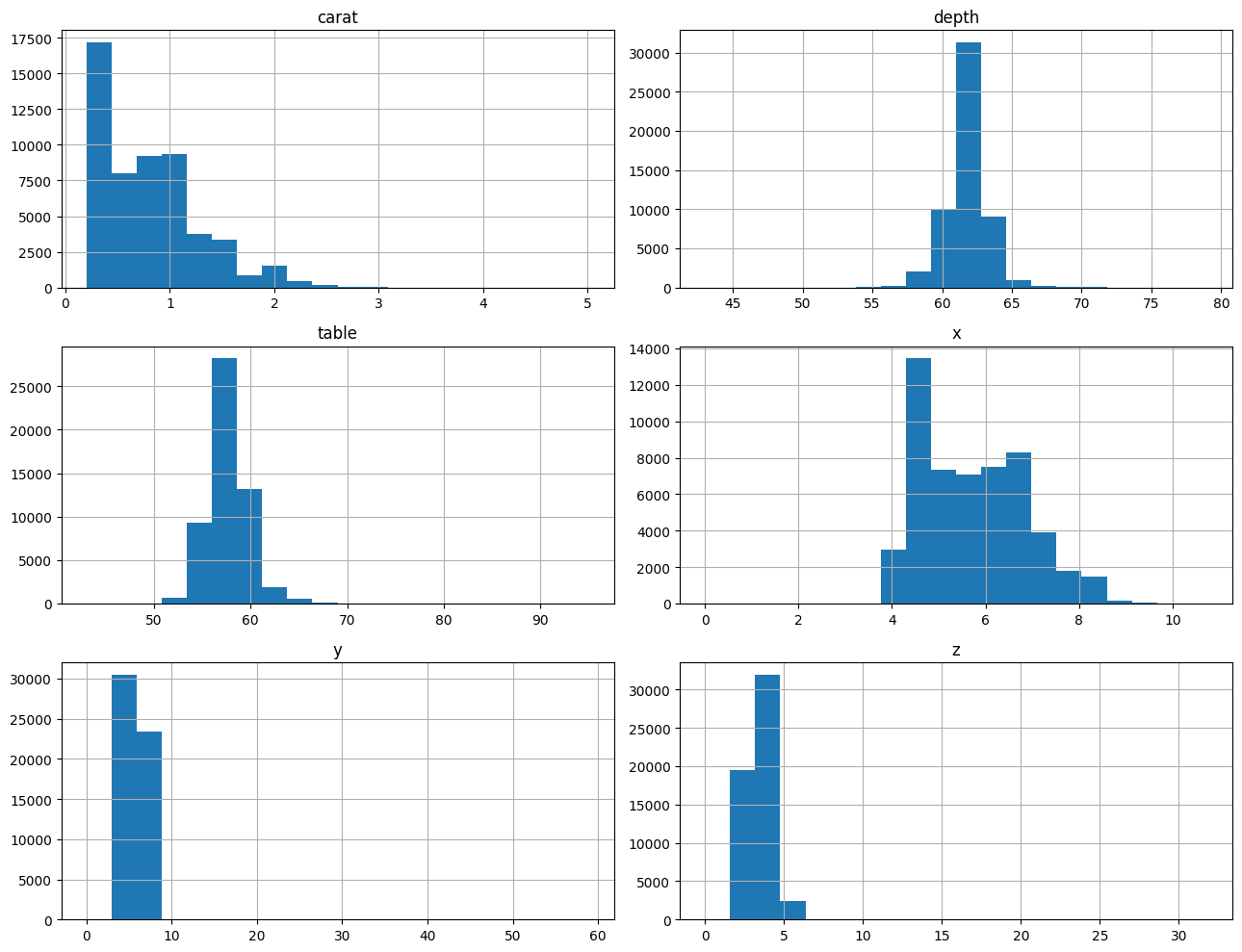
- depth와 table의 경우 중심 대칭 분포를 보이고 있음
- y와 z는 값의 변동이 작은 경향
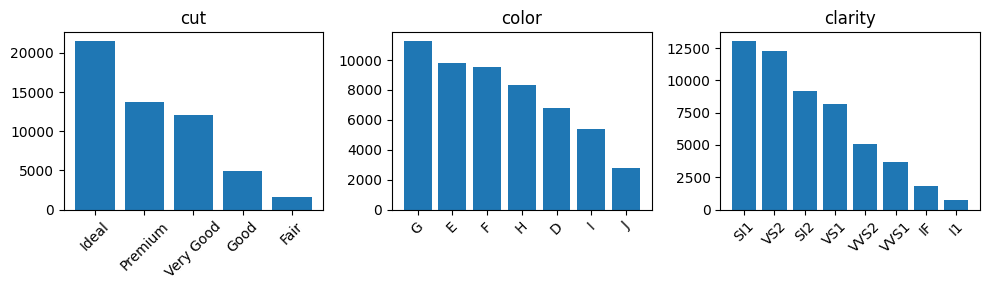
- category형 변수는 서열척도로, 척도별 빈도에 차이를 보임

3. 전처리

결측치는 존재하지 않음
가격 데이터에 극단적인 값이 보이나, 다이아몬드의 경우 품질별 가격 편차가 큰 점을 감안하여 이상치로 보지 않기로 결정
categorical자료는 서열척도로 범주에 위계가 존재하여 LabelEncoding 대신 상위 범주에 높은 값을 매핑해줌
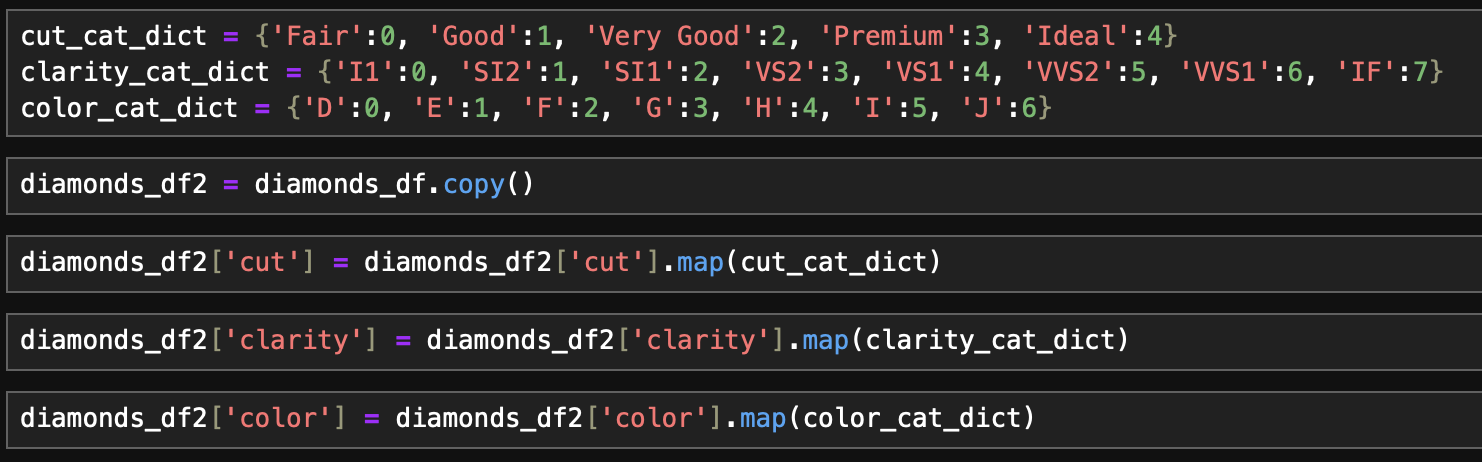
변수별 측정 단위가 다른 점을 감안하여 수치형 변수를 표준편차표준화(StandardScaler) 적용
전처리 결과

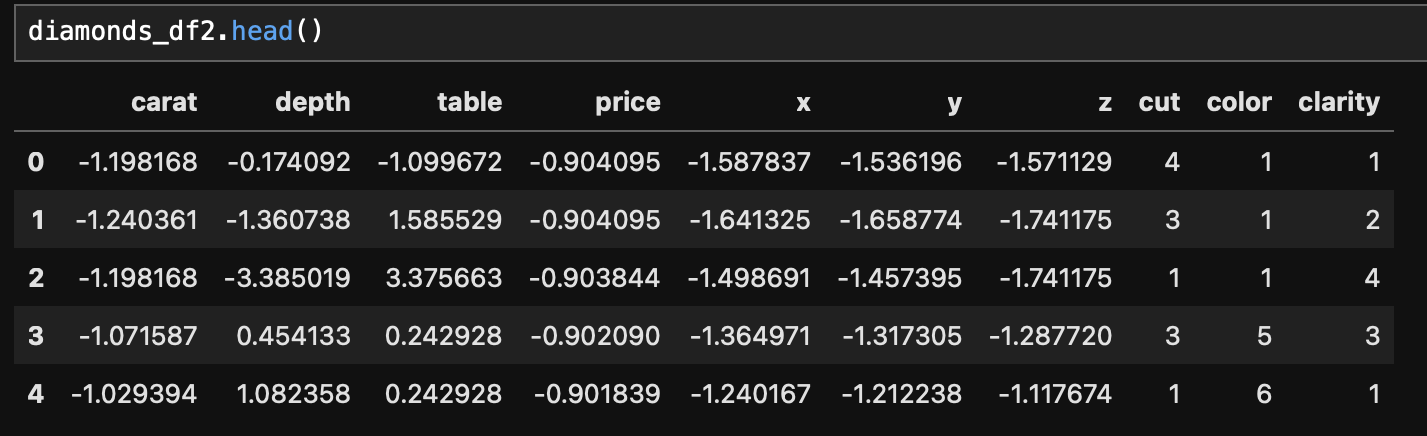
4. 선형회귀 가정 확인

선형성
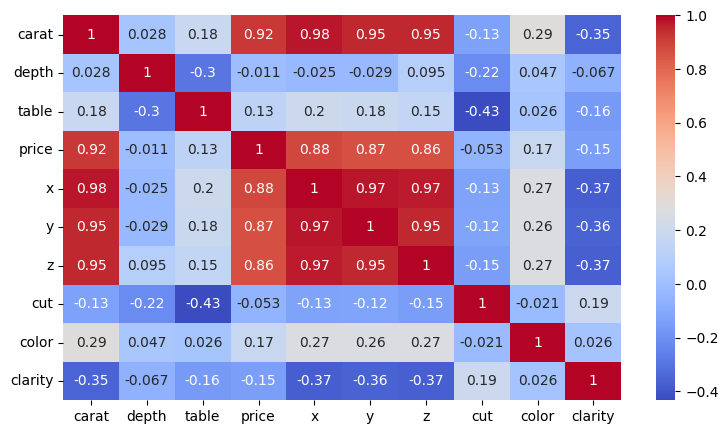
- 종속변수 price와 타 변수의 선형 상관관계를 살펴보면 carat, x, y, z 변수와 강한 선형 상관관계가 확인
- 그런데 carat과 x, y, z 변수도 강한 선형 상관관계를 보임
- table, depth 변수는 수치형 변수임에도 불구하고 종속변수 price와 선형 관계를 보이지 않으므로 변수에서 제거 결정
- carat 변수를 모델에서 제거하여 변수 간 다중공선성 문제를 해소
정규성
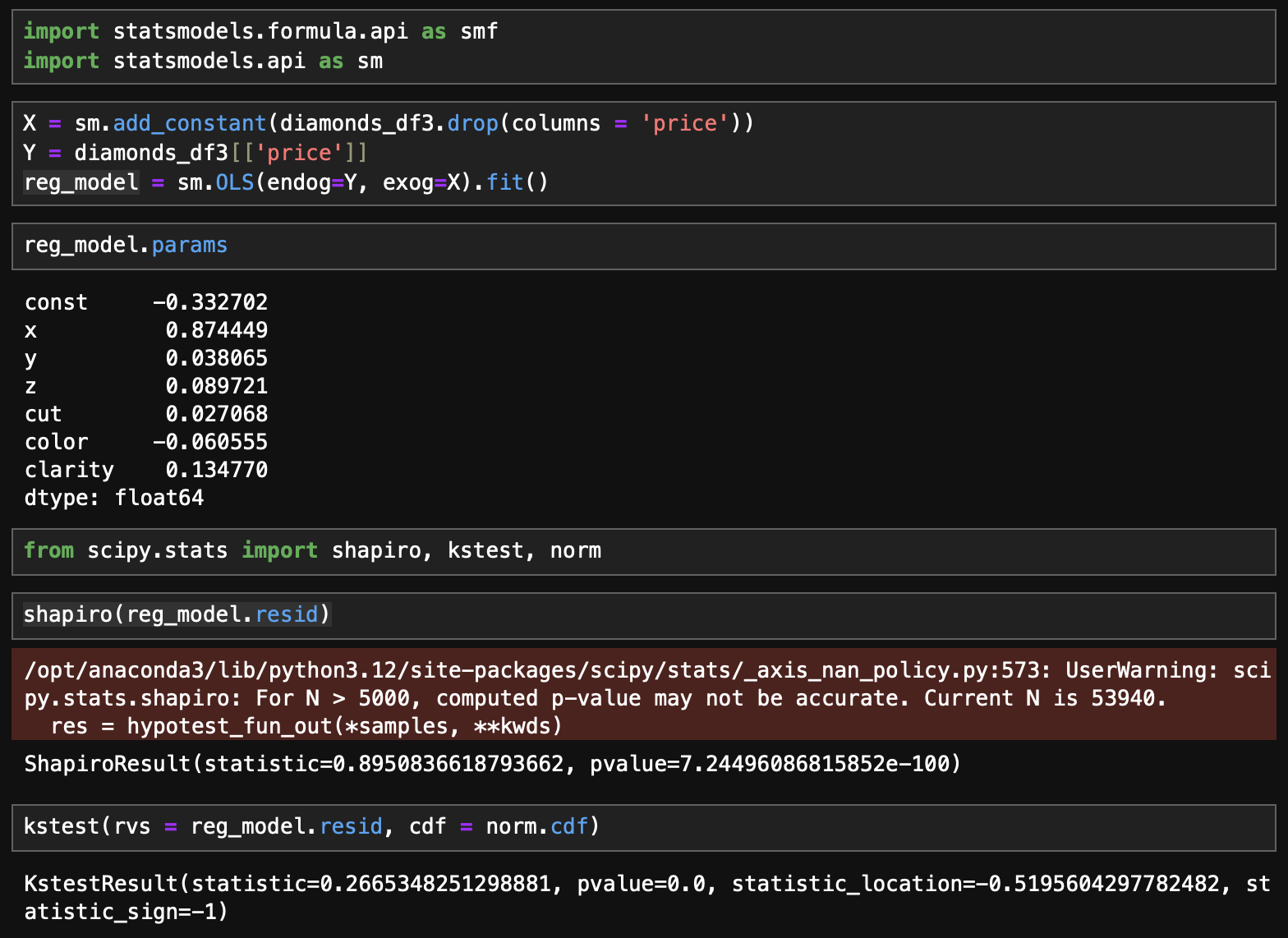
- 단순선형회귀 적합 후 잔차에 대하여 shapiro검정과 kolmonorov-smirnov 검정 수행
- 잔차가 정규성을 따른다는 귀무가설 하에서 두 검정 모두 극도록 낮은 p_value를 반환하며 귀무가설을 기각
  (표본의 크기가 매우 큰 경우에는 검정의 민감도가 높아져 정규성을 조금만 따르지 않아도 귀무가설이 기각될 수 있음)
등분산성
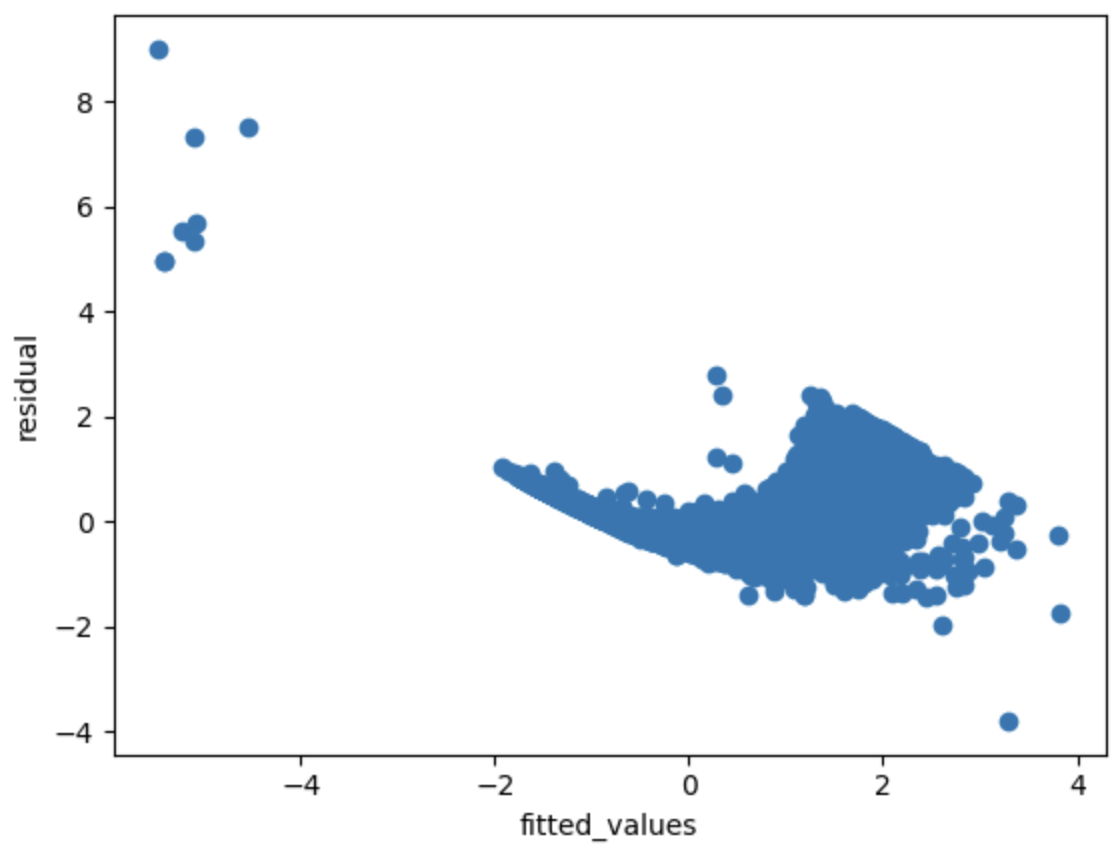
- 추정치(fitted_value)와 잔차(residual)의 산포도를 확인해보면 매우 큰 잔차와 매우 작은 잔차가 일부 확인됨
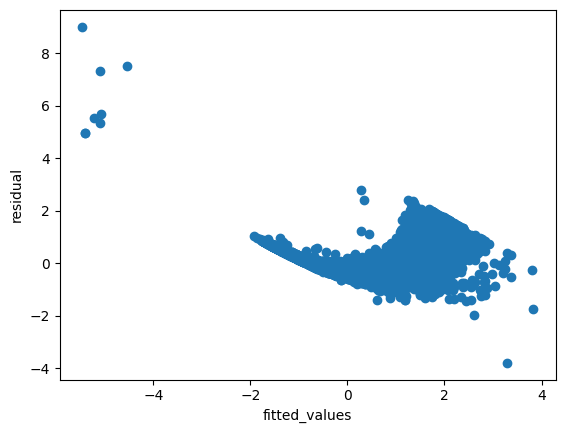
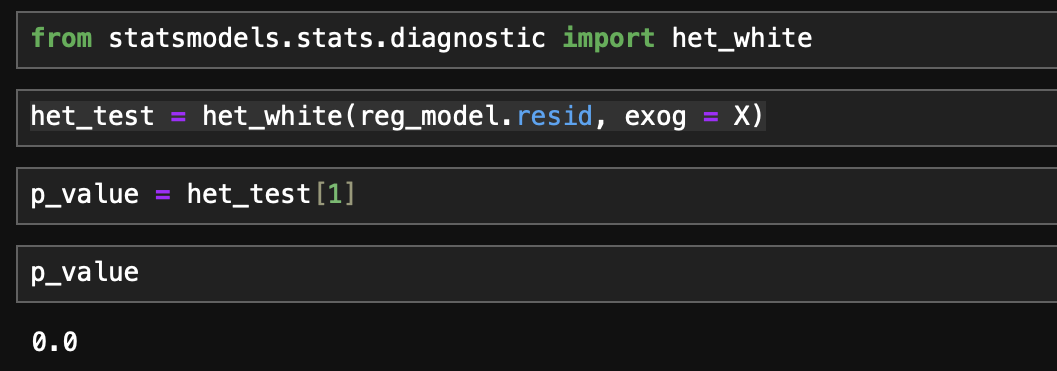
- 잔차가 등분산을 따른다는 귀무가설 하에서 White test를 수행한 결과 p_value가 0으로(극히 낮은 값) 귀무가설을 기각
독립성
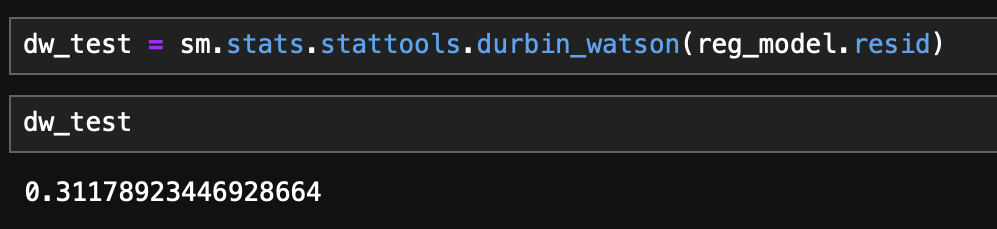
- Durbin-Watson 값은 약 0.3으로 잔차가 양의 상관관계를 갖는 것으로 확인됨
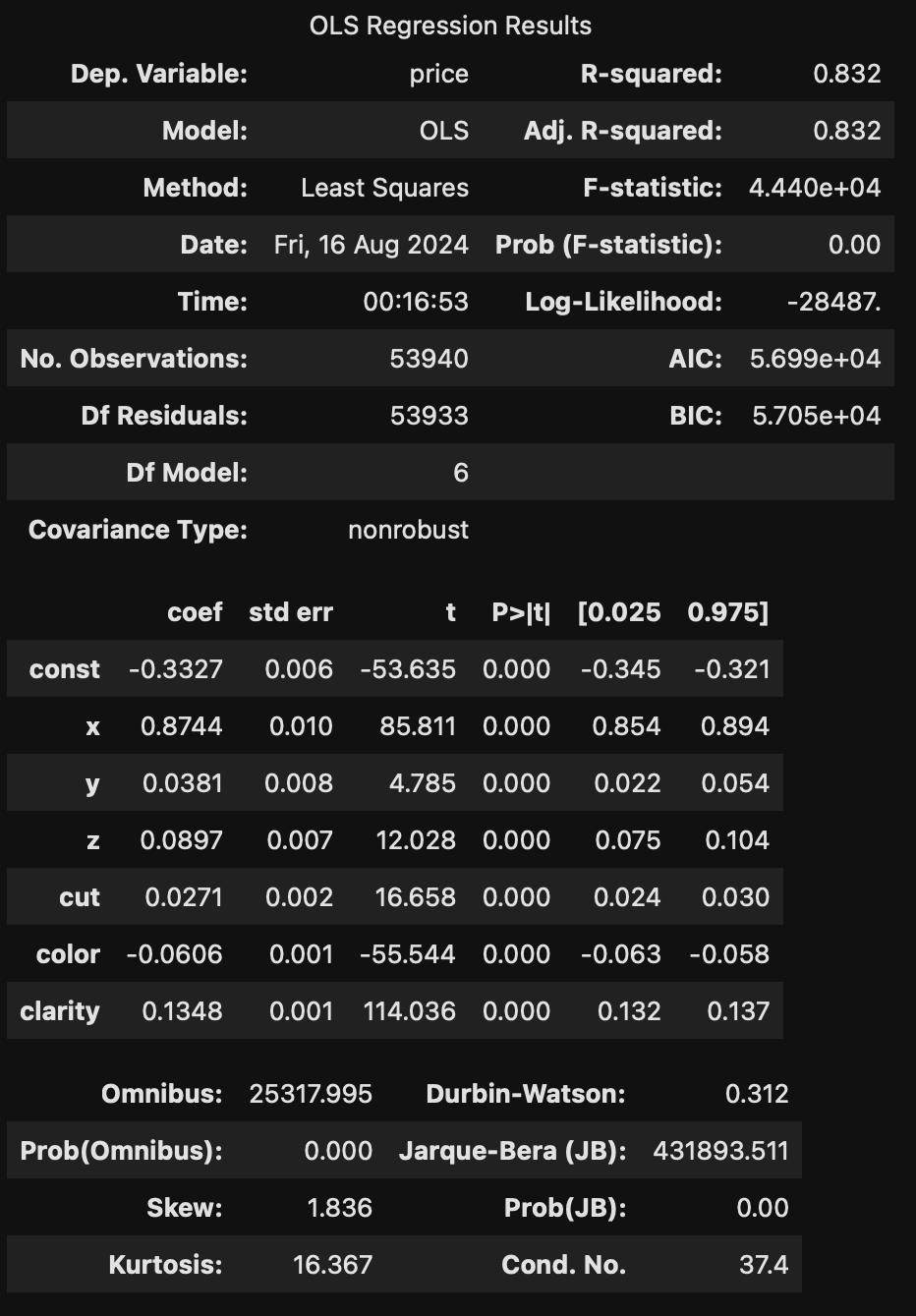
회귀계수 추정 결과
- 놀랍게도 모든 회귀계수의 p-value가 0.05 미만으로 통계적으로 유의미하게 나오는데 그 이유는 std_err에서 확인할 수 있다.
- std_err는 모분산(표본분산)을 표본의 수로 나눈 값으로 표현할 수 있는데, 표본의 크기가 매우 크면 이 std_err가 극히 낮아지는 것이다.
- 즉 정규성, 등분산성, 독립성을 위반한 상태로 회귀직선을 구하였으나 표본의 크기가 워낙 커 선형으로는 현재 추정한 회귀식이 데이터를 잘 설명한다고 말할 수 있는 것이다.
  (선형 회귀모형이 본 데이터를 가장 잘 설명한다는 것은 아니다!)