[통계] 데이터 분석과 통계

1. 모집단과 표본

• 모집단(population): 수집 가능한 모든 관측값들을 모은 집합

• 표본(sample): 실제로 수집되는 모집단의 일부분에 해당하는 관측값들의 집합

• 통계학의 주된 목표: 주로 통계적 추론

  • 표본에 포함되어있는 정보를 분석하여 모집단에 관하여 추론

  • 추론에 수반되는 불확실성도 측정(중요)

• 모집단을 알고 있는 경우 통계적 추론은 의미가 없으며, 모집단을 이용한 패턴(경향) 파악이 적합(통계분석이 아닌 머신러닝의 영역)

2. 기술통계

• 우리가 주로 알고 싶은 것은 관측값 자체가 아닌 관측값들의 분포

  • 관측값들의 분포를 알아야 일반적인 경향성을 파악할 수 있음

• 기술통계는 데이터의 분포를 정량화된 수치로 표현하는 것, 분포의 대푯값

  • 분포가 대칭인 경우와 비대칭인 경우 사용하는 대푯값은 달라질 수 있음

  • 대칭인 경우 주로 평균과 표준편차, 비대칭인 경우 중앙값 등을 활용

3. 추론통계와 정규성

• 통계적 추론은 모집단 분포의 대푯값(즉 모수)을 표본을 통해 추정해내는 과정

• 추론에는 불확실성이 수반되며 이러한 불확실성을 측정하기 위해서는 분포에 대한 전제조건이 필요

  • 특정한 값이 관측될 확률이 90%라고 말하려면 그 특정한 값이 어떠한 분포를 보이며 관측치가 분포 상 어디에 위치하는지 알아야 하는 것

• 그런데 문제점은 분포의 종류가 너무나 많아 어디에 어떤 분포를 가정해야 할지 막연하다는 것

• 일반적으로 대칭분포는 많은 사회 현상에서 나타나고 있으며, 그 중 정규분포는 평균과 표준편차만으로 분포를 설명할 수 있는 커다란 장점이 있어 주로 활용

  정규분포의 확률밀도함수

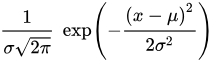
  • 표본의 크기가 충분히 크다면 표본평균의 분포가 정규분포를 따르며(중심극한정리) 이를 통해 표본평균을 이용해 모수에 대한 가설검정이 가능

  • 표본의 크기가 작은 경우 모집단의 정규성을 가정해야 t분포, 카이제곱분포, F분포 등 파생분포를 사용할 수 있으므로 정규성 가정은 매우 중요한 가정이라고 볼 수 있음