Chap3 Linear Regression

3.1.1 Estimating the Coefficients

RSS를 최소화 하는 OLS 방법으로 계수를 추정

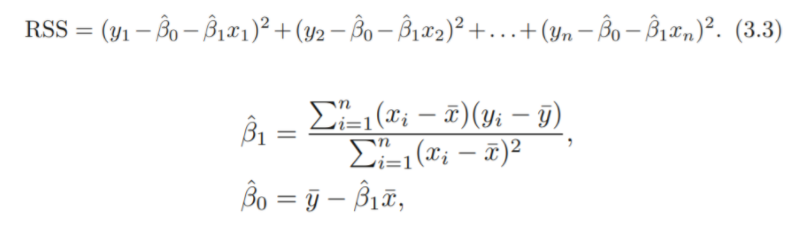
3.1.2 Assessing the Accuracy of the Coefficient Estimates

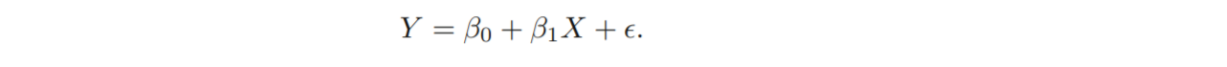
$B_0$ : The expected value of $Y$when $X=0$

$B_1$ : The avearge increase in $Y$ associated with a one-unit increse in X.

$e :$ What We miss with this simple model. ( $X$와 independent 하다고 가정)

→ 위와 같은 true relationship에서 Coefficients를 추정함.

• Unbiased :

  Our estimates 가 정확히 $B_0,B_1$은 X. But, huge number of data sets에서 얻은estimates 들의 평균은 $B_0,B_1$이 될 것.

• Standard error ( 표준오차 : 표본 통계량의 표준 편차)

각 표본 통계량들에 대한 표준 편차를 구할 수 있음

추정치가 실제 값에서 평균적으로 얼마나 떨어져 있는가

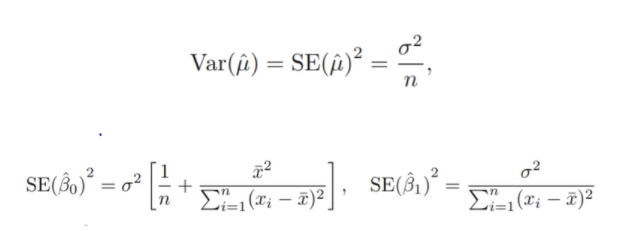
: n이 커질수록 작아짐
: 계수추정치의 표준오차는, x들이 spread out 되어있을수록 작아짐.

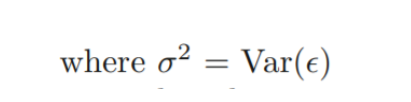
→ errors ($e_i$) for each observations are uncorrelated with common variance (독립, 등분산 가정)

• Residual Standard Error : estimate of sigma

• t-statistics

  Our estimate of $B_1$이 0에서 얼마나 멀리 떨어져 있어야, $B_1$이 0이 아니라고 말 할 수 있겠는가?

  0 (귀무가설에서 설정한 $B_1$의 값) 과 $B_1$의 추정치의 통계적 거리를 계산해 그 값이 충분히 크면 귀무가설 기각

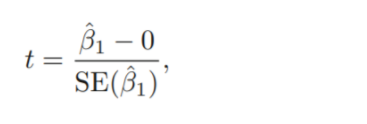
: t-distribution을 따르고, degree of freedom은 n-2
: standard error가 작으면 , t-value가 커짐.

• P-Value

  검정통계량( t-statistics)의 값보다 크거나 같은 경우가 있을 확률

  p-value가 충분히 작으면, t-statistics 즉 0과의 통계적거리가 충분히 크다고 판단하고 귀무가설을 기각함.

  보통 유의수준에 따라 1% , 5%로 그 기준을 설정

3.1.3 Assessing the Accuracy of the Model

Model이 data에 얼마나 잘 fitting 되어있는가

• RSE(Residual Standard Error)

  : regression line과 response가 평균적으로 얼마나 차이가 나는가

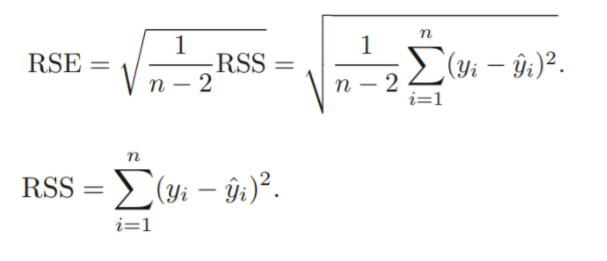
lack of fit(적합성 결여)에 대한 척도로 사용됨

• $R^2$

  : 회귀식에 의해 설명되는 분산의 비율
  : 0-1사이
  : y의 scale에 independent함.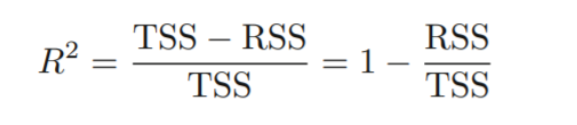

  
  TSS(total sum of squares) : Y의 총변동
  RSS : regression으로도 설명되지 않는 변동
  TSS - RSS : regression으로 설명되는 변동
  → X가 설명해내는 분산의 비율

  1에 가까울수록 → regression에 의해 변동이 많이 설명됨을 의미

  0에 가까울수록 → 잘 설명해내지 못함. (원인 : 모델이 적합하지 않거나, 원래 분산이 크거나, 아니면 둘다)

  : RSE보다 해석에 용의함

  : application 분야에 따라 good $R^2$에 대한 기준이 달라질 수 있어 애매함

  : X와 Y의 linear relationshop에 대한 척도로 사용되기도 함 ( correlation)

  : simple linear regression에서는 $R^2 = r^2$(squared correlation)

  correlation

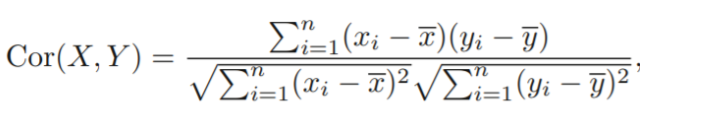
• F-Statistics(3.2.2) (모델평가기준)

3.2 Multiple Linear Regression

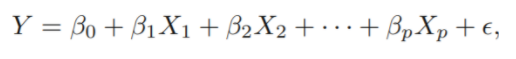
$B_j$ : The avearge effect on $Y$ of a one unit increase in $X_j$, holding all other predictors fixed.

3.2.1 Estimating the Regression Coefficients

: RSS를 최소화하는 OLS방법론 사용

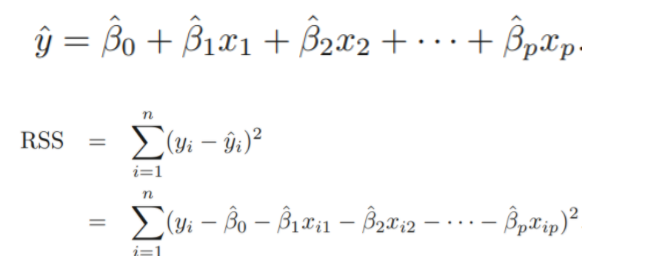
: Simple에서는 다른 predictors를 ingnoring했지만, Multiple linear Regression에서는 다른 변수들의 효과를 fix한 것이므로, 동일 predictor의 동일 reponse에 대한 유의성은 모델에 포함된 변수에 따라 달라질 수 있음.

ex >

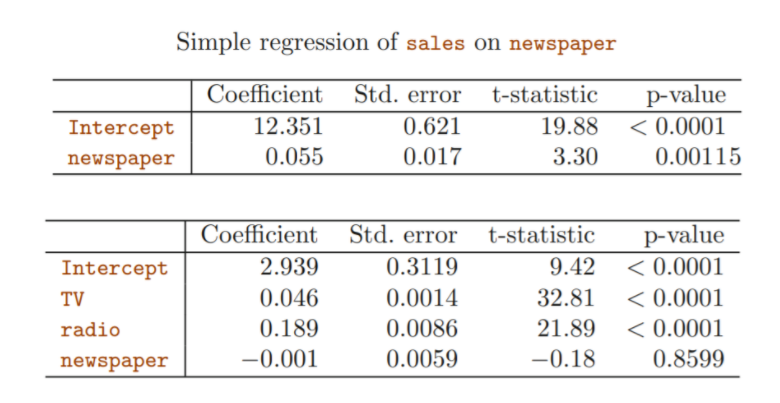
: 다른 변수들이 고려되었을 때, newspaper는 reponse에 대해 더이상 유의한 변수가 아님.

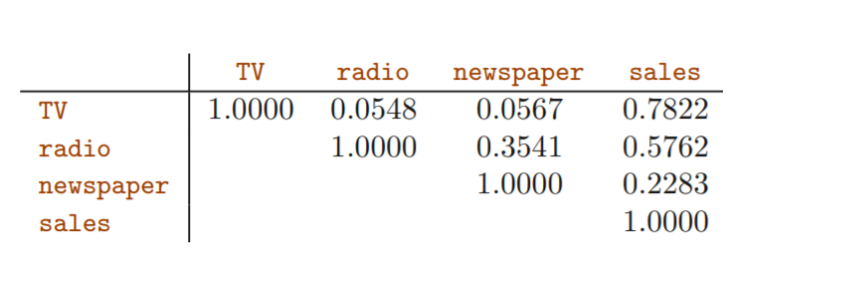
newspaper와 radio의 correlation이 0.35

spending more on radio → spending more on newspaper : 경향성

따라서, newspaper가 sales에 actual impact가 없는데도, 다른 변수들이 ignoring 된 상태에서는 유의하다는 결론이 내려졌음(simple)

그러나 다른 변수의 효과가 fix된 상태(Multiple)에서는 더이상 유의하지 않음

3.2.2 Some Importance Questions

One : Is there a Relationship Between the Response and Predictors?

따라서, F-statistics는 항상 1보다 큰 값을 가지며, $H_0$을 기각하기 위해서는 F-statistics가 충분히 커야함.

partial effect :

변수 한개에 대한 squre of t-statistics = F-statistics (q=1) (다른 변수들이 adjusting 되었을 때 해당 변수가 reponse에 유의한 영향을 주는가)

Two : Deciding on Important Variables

F-statistics를 통해, 적어도 하나의 변수가 유의하다는 결론을 내린 뒤, 쓸모있는 변수와 그렇지 않은 변수를 골라내야함 :
Variable Selection (chap6)

• 어떤 (변수들을 포함하고 있는) model이 가장 best인가? (criteria)

  → 기준 : $Maalow's Cp$ , $AIC,BIC,adjusted-R^2$

• p개의 변수가 있을 때, 고려해야하는 모델의 개수 : $2^p$

: smaller set of models를 고려하기 위한 방법론 필요

Forward Selection :

null model에서 시작해서 lowest RSS을 주는 변수 선택해서 추가

RSS가 더이상 낮아지지 않을 때까지 반봅

Backward Selection :

Full model에서 시작해서 largest p-value를 가지는 변수 제거(the least statistically significant)

remaining variables가 모두 특정값보다 낮은 p-value를 가질 때까지 반봅

Mixed Selection :

Forward selection과 Backward Selection의 combination

Model에 있는 모든 변수가 sufficiently low p-value를 가지고, Model에 포함되지 않은 모든 변수가 large p-value를 가질때까지 forward , backward 방법 반복.

Three : Model FIt

$RSE , R^2$

: $R^2$는 변수의 개수가 많아질수록 그 값이 항상 커짐(evne if those variables are only ewakly associated with the response)

: $RSE$ increase in p 에 비해 RSS 가 적게 감소하면, RSE는 증가할 수 있음 (변수의 개수가 많아진다고 무조건 그 값이 내려가지는 않음. 변수의 개수에 대한 고려가 있기 때문)

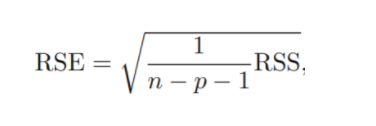
numerical한 Statistics로 담기지 않는 정보는 graphic summeries 를 통해 발견할 수 있음.

Four : Predictors

Prediction과 관련하여 uncertainty가 존재(추정된 값은 정확한 값이 아님)

→ confidence / prediction interval을 사용함

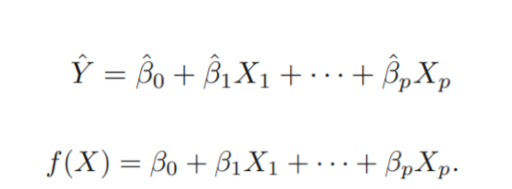
model에서 계수는 추정되기 때문에, 정확한 값이 아님. 이를 해결하기 위해

→ confidence interval 사용

새로운 x에 대한 y를 추정하고자 할 때는 random error 또한 고려되어야 함

→ prediction interval (추정된 값에 대한 분산 + random error에 대한 분산이 둘다 고려됨)

(따라서 confidence interval보다 그 구간이 넓음)

이외에도, model bias가 존재할 수 있음 (ex. linear model이 correct하다는 가정하에 모델링. 하지만 이 가정이 틀릴수도 있음)

3.3 Other Consideration in the Regression Model

3.3.1 Qualititive Predictors (질적 설명변수)

• 레벨(수준)수가 2인 설명변수

두 개의 가능한 값을 가지는 지시변수(indicator variable) 또는 가변수(dummy variable)을 생성

ex) Gender(수준이 2개인 질적 설명변수) Balance(반응변수)인 회귀 모형

< 회귀 계수 해석 >
$β_0$ : 남성들의 평균 Balance
$β_0$ + $β_1$ : 여성들의 평균 Balance
$β_1$ : 여성과 남성의 Balance 평균의 차이

가변수의 p-value = 0.6690 로 매우 크므로 여성과 남성의 평균 Balance의 차이가 존재한다는 통계적 근거가 없음

+) 가변수를 0/1로 코딩하는 대신 -1,1로도 코딩 가능

< 회귀 계수 해석 >
$β_0$ : 성별을 고려하지 않은 전체 평균 Balance
$β_1$ : 여성들이 평균보다 높은 정도, 남성들이 평균보다 낮은 정도

• 레벨 수가 3 이상인 질적 설명변수

레벨 수가 3 이상인 경우 , 하나의 가변수로 모든 값을 나타낼 수 없으므로 가변수를 추가

ex) 레벨 수가 3인 Ethnicitiy 변수에 대해 2개의 가변수 생성

가변수의 개수 : (레벨 수) - 1
가변수가 없는 레벨 : African American (기준)

< 회귀 계수 해석 >
$β_0$ : African American의 평균 Balance
$β_1$: Asian과 African American 간 평균 Balance 차이
$β_2$: Caucasian과 African American 간 평균 Balance 차이

두 가변수의 p-value = 0.7740, 0.8260 으로 매우 크므로 인종별 평균 Balance의 차이가 존재한다는 통계적 근거가 없다.

3.3.2 Extension of the Linear Model

Standard Linear Regression Model은 실제로는 잘 성립하지 않는 두 가정을 사용

1. 가산성(Additivity) : $X_j$의 변화가 반응변수 $Y$에 미치는 영향이 다른 설명변수에 독립적

2. 선형성(Linearity) : $X_j$의 한 유닛의 변화로 인한 $Y$의 변화는 $X_j$의 값에 관계없이 상수

   → 이러한 두 가정을 완화하는 방법

Removing the Additive Assumption

• 상호작용항 추가 모형

표준 선형 회귀 모형

$Y = β_0 + β_1X_1 + β_2X_2 + ϵ.$

X2에 관계없이 X1이 한 유닛 증가하면 Y는 β1만큼 증가

상호작용항을 포함하도록 모델을 확장하면,

$Y = β_0 + β_1X_1 + β_2X_2 + β_3X_1X_2 + ϵ$

$\overset{˜}{β_1} = β_1 + β_3X_2$, $\overset{˜}{β_1}$ 은 X2에 따라 변하므로 $Y$에 대한 $X_1$의 효과는 상수가 아님 ($X_2$에 독립적이지 않음)

→ 따라서 상호작용항을 포함하면 가산성 가정을 완화

ex) Radio와 TV, Radio*TV로 Sales를 예측하는 선형 모델

→ β3 : Radio 한 유닛 증가에 대한 TV의 효과의 증가 (또는 그 반대)로 해석 가능

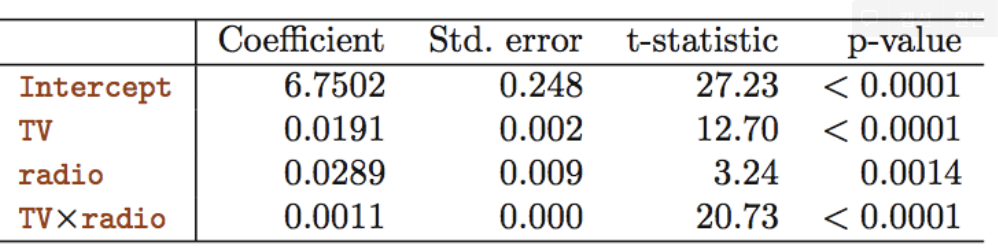
→ TVxRadio 의 P-value < 0.0001 이므로 $H_a : β_3 \neq 0$
주효과만 포함하는 모형보다 상호작용항을 포함하는 모형이 더 낫다.

• Hierarchical Principle에 의해 상호작용항을 포함하면 주효과는 p-value가 유의하지 않더라도 모형에 포함되어야 한다.

• 양적변수(Income) + 질적변수(Student 여부)인 경우

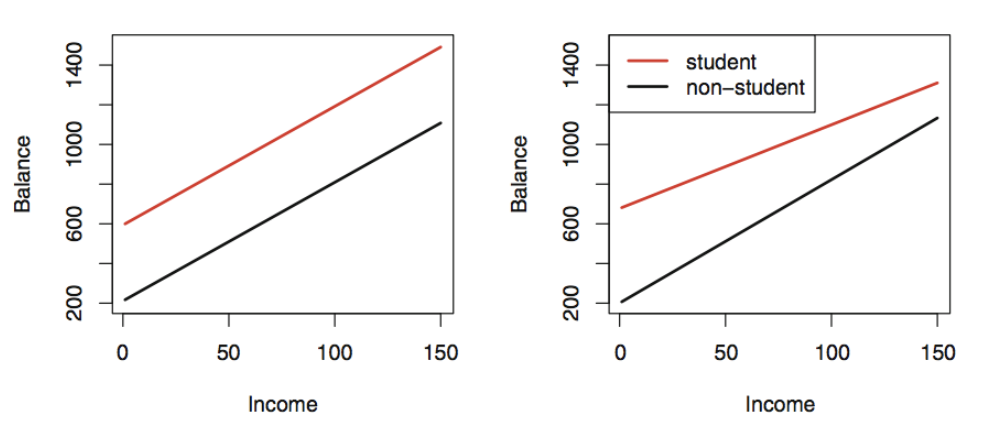
상호작용항이 없는 경우 : 두 개의 평행한 직선 (절편은 다름)
상호작용항이 있는 경우 : 기울기와 절편이 다른 두 직선

Non-linear Relationships

반응변수와 설명변수 사이의 상관관계가 비선형적일 수 있다.
→ 비선형 상관관계를 수용하도록 Polynomial Regression(다항 회귀)를 사용하여 선형모델을 확장

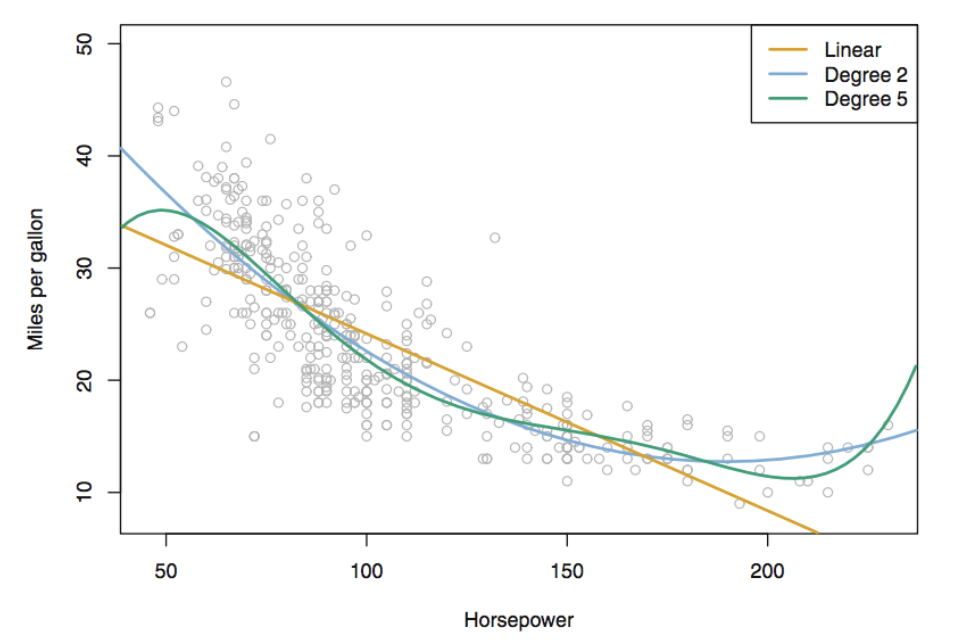
데이터가 이차함수 형태(비선형적 상관관계)를 띠므로

$mpg = β_0 + β_1 × horsepower + β_2 × horsepower^2 + ϵ$

으로 적합하면

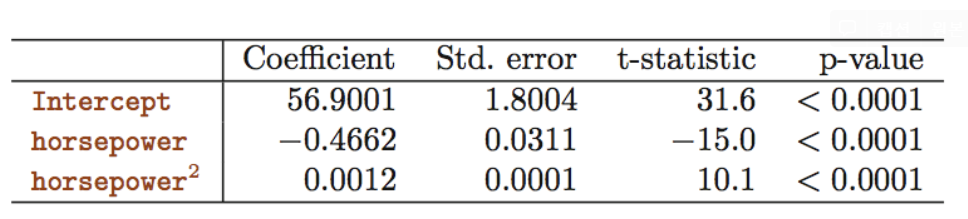
$horsepower^2$ 의 p-value가 < 0.0001로 매우 유의하므로 모형에 포함하는 것이 적절

3.3.3 Potential Problems

선형 회귀 모형을 적합할 때 발생할 수 있는 문제들

1. Non-linearity of the response-predictor relationships (반응변수와 설명변수간의 비선형성)

   선형 회귀 모형은 설명변수과 반응변수 간의 선형성을 가정

   • 잔차 그래프를 그려 비선형성을 식별
   1. 단순선형회귀모형 : 잔차($e_i =y_i − \overset{ˆ}{y_i}$) 대 설명변수($x_i$) 그래프
   2. 다중선형회귀모형 : 잔차($e_i =y_i − \overset{ˆ}{y_i}$) 대 예측치($\overset{ˆ}{y_i}$) 그래프

   → 인지할만한 패턴이 있으면 선형모델에 문제가 있을 수 있음

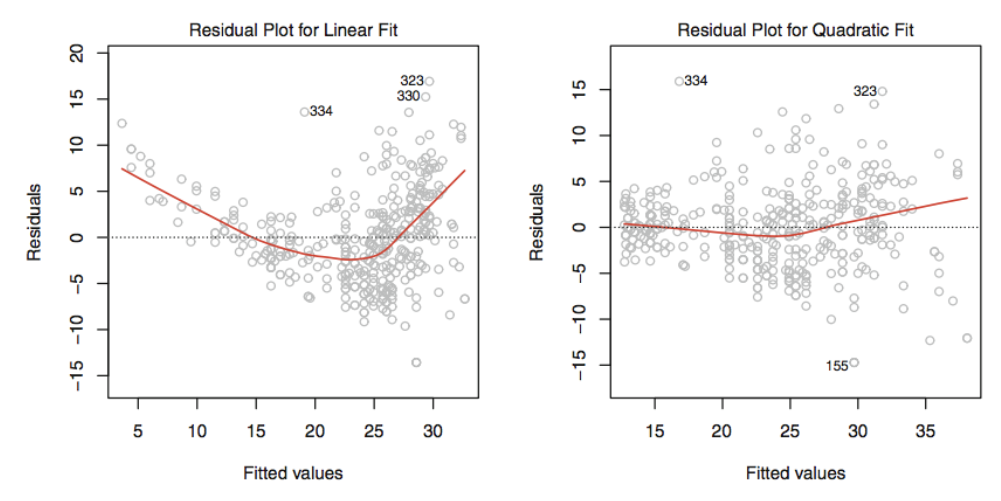
데이터의 비선형성 → 이차항을 포함하는 모델 → 패턴이 거의 보이지 않음 → 이차항이 데이터의 적합을 향상

따라서, 잔차 그래프가 비선형 상관성을 띠면 $log X, √X$, and $X^2$와 같이 설명변수들을 비선형 변환

2. Correlation of error terms (오차항들의 상관성)

   선형 회귀 모형은 오차항들이 서로 상관 되어있지 않음을 가정

   ex) $ϵ_i$가 양수라는 사실이 $ϵ_{i+1}$의 부호에 영향을 주지 않음

   오차항이 상관되어있으면,

• 추정된 표준오차가 실제 표준오차를 과소추정하는 경향 → 신뢰구간과 예측구간은 계산된 수치보다 좁을 것

• 모델과 연관된 P-value가 실제 수치보다 낮게 나와 모수가 통계적으로 유의하다고 잘못 결론 내릴 수 있음

  이러한 상관성은 시계열 데이터에서 자주 발생.

  잔차를 시간에 따라 그렸을때 상관성이 있으면 패턴이 인지됨.

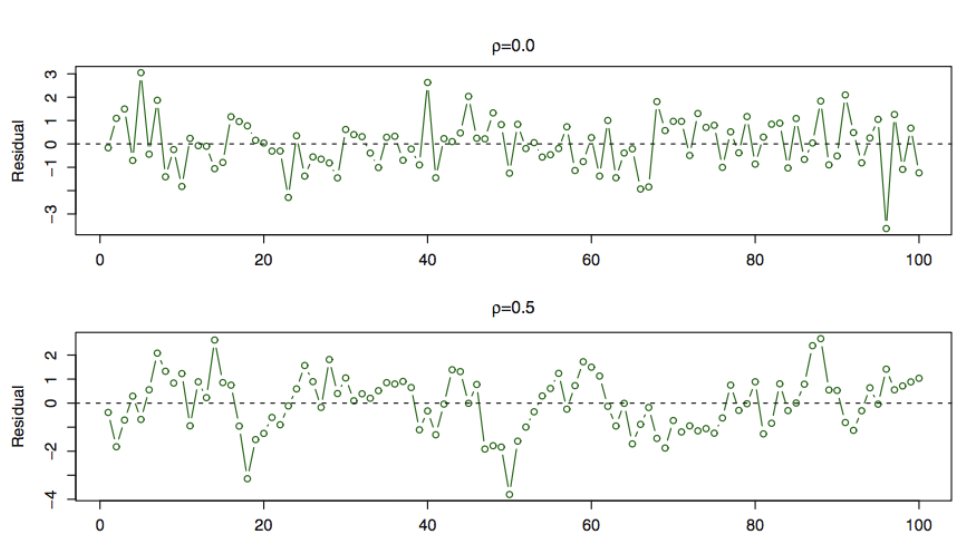
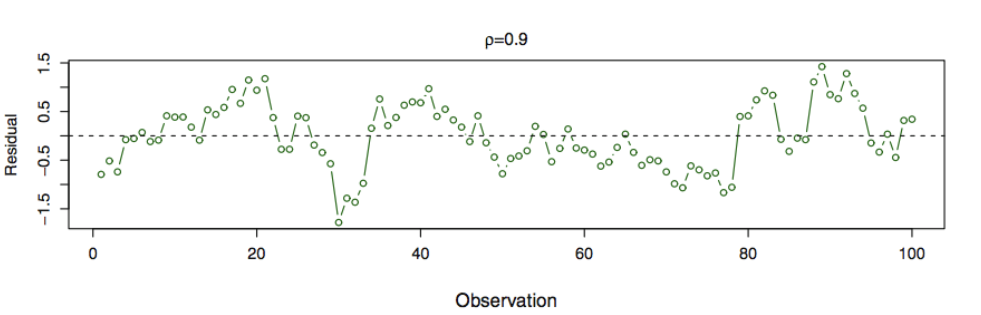
첫번째 그림 - 오차에 상관성 없음
두번째 그림 - 패턴이 명확하지 않음
세번째 그림 - 이웃하는 잔차끼리 유사한 값을 가짐 → 패턴이 존재 → 상관성 가짐

3. Non-constant variance of error terms (오차항의 분산이 상수가 아닌 경우)

   선형 회귀 모형은 $Var(ϵ_i) = σ^2$ 을 가정, 표준오차, 신뢰구간, 가설검정은 이 가정에 의존한다.

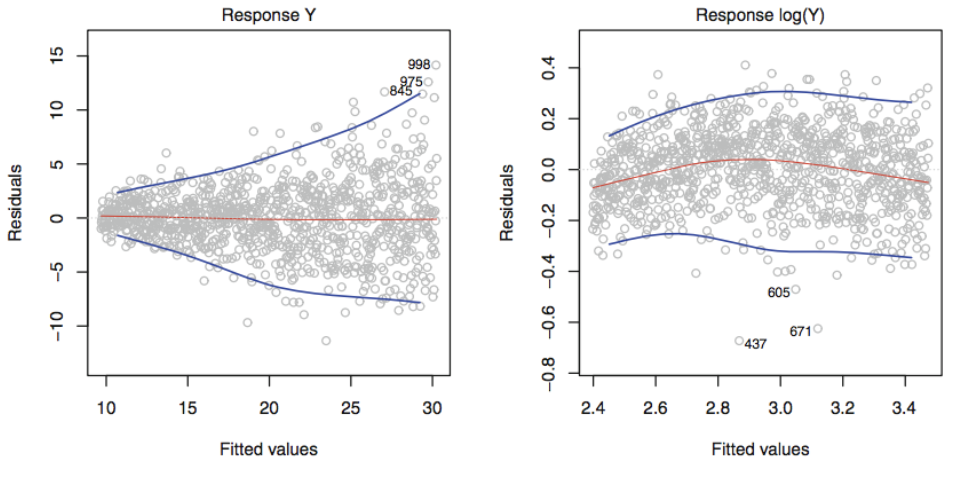
왼쪽 그래프 : 오차항들의 분산이 깔대기 모양의 이분산성을 띤다.
오른쪽 그래프 : Y를 $logY$나 $√Y$ 같은 concave 함수를 사용하여 변환 (그래프는 $logY$로 변환) → 이분산성 완화

반응변수가 원관측치의 평균인 경우 원관측치의 분산이 $σ^2$인 경우
반응변수의 분산은 $σ_i^2= σ^2/n_i$ → 이 경우 Weighted Least Square방법으로 $w_i=n_i$

4. Outliers (이상치)

   이상치는 $Y_i$가 모델이 예측한 값과 크게 다른 점

   이상치는 설명변수의 값이 특이한 점이 아니므로 Least Square 적합에 영향을 주진 않지만
   RSE값에 영향을 주므로 신뢰구간과 p-value, $R^2$ 계산에 영향을 준다.

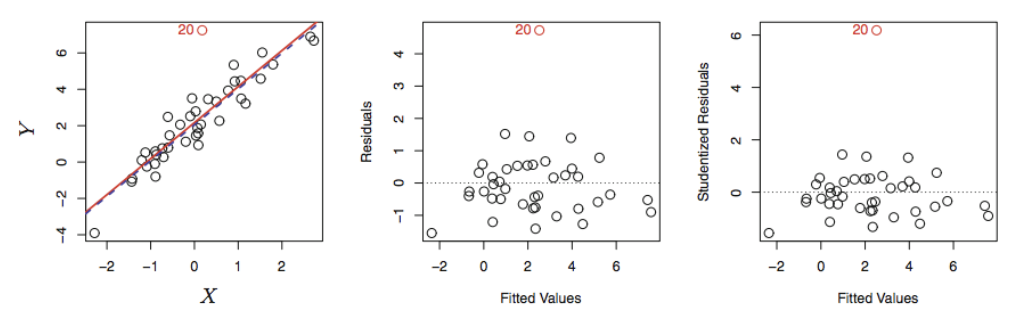
잔차 그래프(가운데 그래프)로 이상치를 식별할 수 있지만 이상치라고 판단하기 위해서는

스튜던트화 잔차(오른쪽 그래프)를 보는 것이 적절하다. (스튜던트화 잔차 = 잔차 / 추정표준오차)

스튜던트화 잔차 절대값이 3 이상이면 이상치

outlier는 missing predictors등과 같은 model deficiency등을 indicate하기도 함. 따라서 주의깊게 살펴볼 필요 있음.

5. High-leverage points (레버리지가 높은 관측치)

   설명변수 $X_i$가 보통 수준과 다른 점

   leverage가 높은 관측지를 제거하면 최소제곱 추정치에 큰 영향 → 추정 회귀선에 영향

   • 레버리지 통계량

$h_i = \frac {1}{n} + \frac{(x_i − \overset{-}{x})^2}{\sum_{i′=1}^{\lfloor n \rfloor}(x_i' − \overset{-}{x})^2 }$

hi는 x¯에서부터 xi까지의 거리에 비례, 1/n과 1 사이의 값을 갖는다.

6. Collinearity (공선성)

두 개 또는 그 이상의 설명변수들이 서로 밀접하게 상관

반응변수에 대한 공선성을 가진 변수들의 개별효과를 분리하기 어려울 수 있음

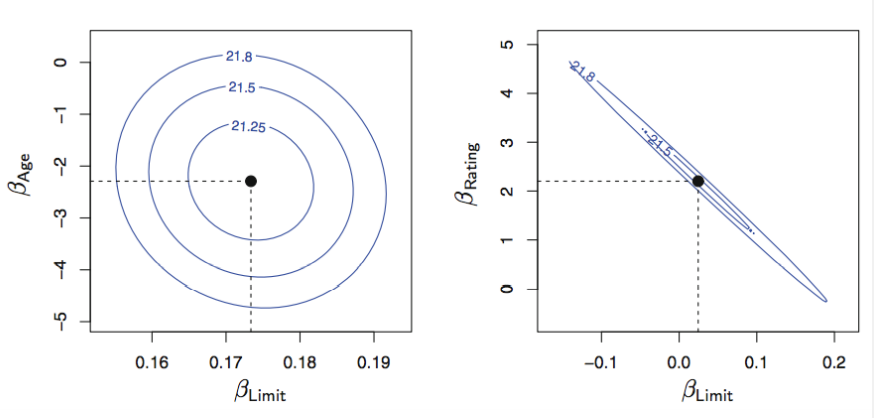
각 타원은 동일한 RSS에 대응하는 계수들의 집합으로 오른쪽 그림을 보면 변수간의 공선성이 존재한다.

공선성은 회귀계수 추정치의 정확성을 낮추므로 에 대한 표준오차가 증가
→ t - 통계량이 작아진다. H0: = 0을 기각하지 못한다. -> the importance of the variable could be msked due to the presence of coliinearity

공선성을 확인하는 방법
1. 상관행렬의 절대값

2. VIF(분산팽창인수) 를 이용하여 다중공선성 (세개 이상의 변수들 사이의 공선성) 확인

VIF(Variance inflation factor): full-model의 의 분산을 자신만의 적합에 대한 의 분산으로 나눈 비

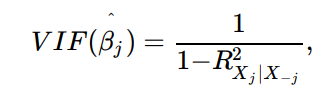
VIF의 최솟값 = 1 (공선성 없음)
VIF가 5 또는 10을 초과하면 문제가 있을 정도의 공선성 존재

공선성을 해결하는 방법
1. 변수들 중 하나 제외
2. 단일 설명변수로 결합

3.4 The Marketing Plan

1. Is there a relationship between advertising sales and budget?

F-statistic=570에 해당하는 p-value가 낮으므로 advertising sales 와 budget에 상관관계가 존재

2. How strong is the relationship?
   이 0.897이므로 설명변수들이 sales의 89.7%를 설명한다.

3. Which media contribute to sales?

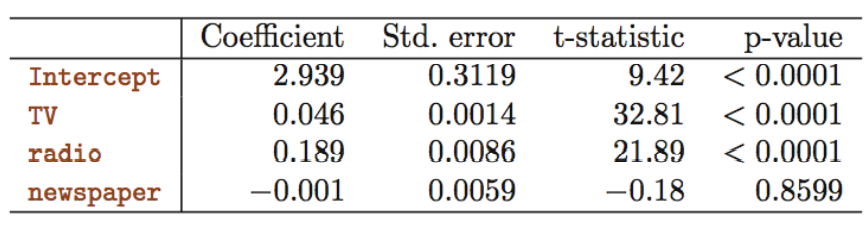
TV와 radio의 p-value는 낮지만 newspaper의 p-value는 높으므로 TV와 radio가 sales와 상관관계가 있다.

4. How large is the effect of each medium on sales?
   TV의 신뢰구간이 (0.043, 0.049) → 0을 포함하지 않으므로 sales 와 상관관계가 있다.
   radio의 신뢰구간이(0.172, 0.206) → 0을 포함하지 않으므로 sales 와 상관관계가 있다.
   newspaper의 신뢰구간이(−0.013, 0.011) → 0을 포함하므로 sales 와 상관관계가 없다.

5. How accurately can we predict future sales?

평균 response를 예측하고자하면 confidence interval을 이용하고, 개별 response를 예측하고자하면 Prediction interval을 이용한다.
Prediction interval 은 irreducible error(ϵ)와 관련된 불확실성을 포함하므로 신뢰구간보다 더 넓다.

6. Is the relationship linear?
   
   잔차 그래프에서 비선형성이 나타난다.

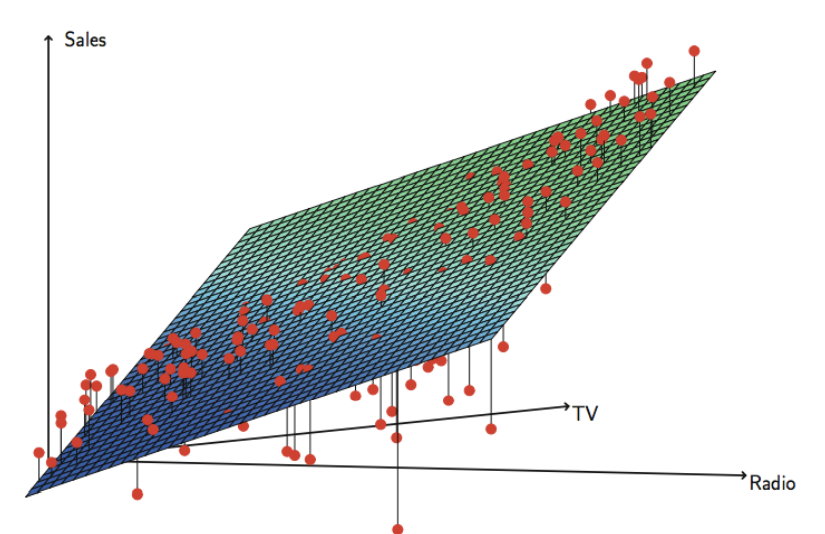
7. Is there synergy among the advertising media?

Yes. 위 그림에서 Advertising 자료가 additive하지 않을 수 있음을 볼 수 있어 상호작용항을 추가하면 값이 90%에서 97%로 증가한다.

3.5 Comparison of linear Regression with K-nearest Neighbors

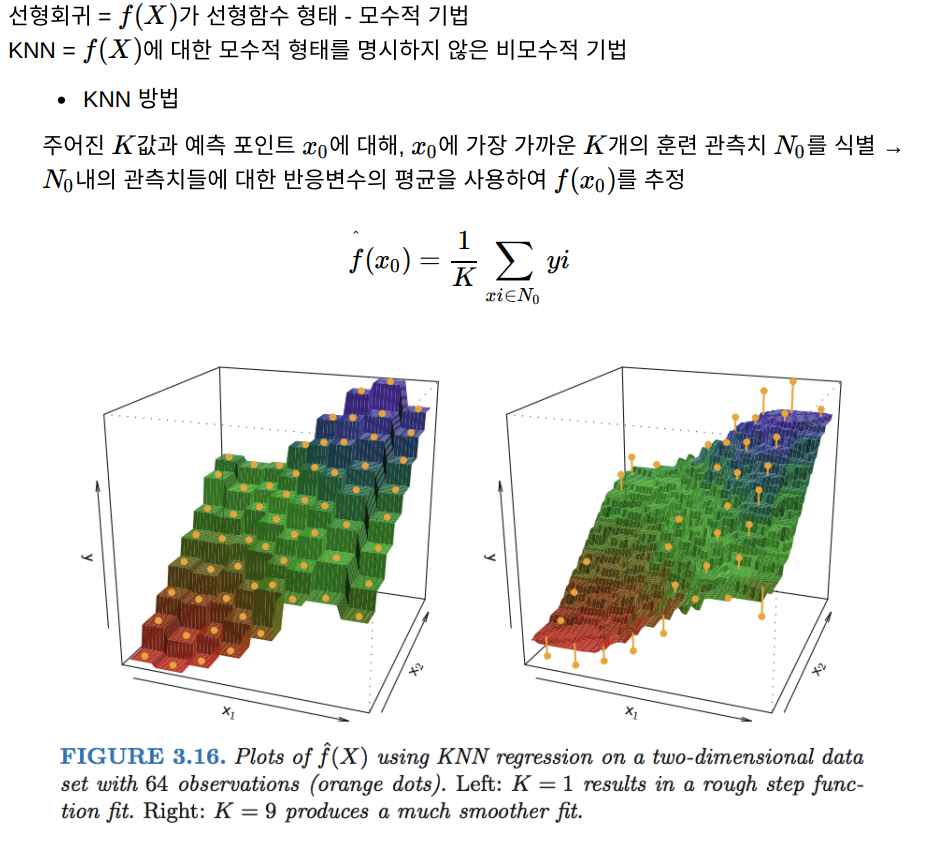
최적의 K는 Bias-Variance tradeoff에 따라 다르다.

K값이 작으면 Bias는 작지만 Variance(가장 가깝다고 판단되는 data set이 바뀌면 그 값도 크게 바뀜)가 크고,
K값이 크면 평활해지면서 Variance가 작아지지만(가장 가깝다고 판단되는 data set이 한개정도 바뀌어도 그 예측값이 크게 달라지지 않음) bias가 커진다.

• 어떤 경우에 선형회귀(모수적 방식)이 KNN(비모수적 방식)보다 더 나은가?

상관관계가 선형 일 때 : 선형회귀
비선형인 경우 : KNN

하지만, 설명변수가 추가됨에 따라 KNN보다 선형회귀가 더 나은 결과를 줄 수 있다.

why ? 차원의 증가는 선형회귀의 MSE를 약간 증가시키지만 KNN의 MSE는 크게 증가
→ 차원이 증가함에 따라 KNN의 성능이 나빠짐

KNN에서 차원의 저주 : 고차원일수록 표본크기가 줄어드는 효과(주어진 관측치에 가까운 이웃이 없어짐)

→ $x_0$에 가장 가까운 $K$개의 관측치들이 p가 클 때 차원의 공간의 으로부터 멀리 떨어져 있을 수 있어 $f(x_0)$의 예측값이 나쁜 KNN적합을 갖게됨.

해석력 관점에서 차원이 낮은 경우에도 MSE차이가 작으면 선형회귀를 KNN보다 선호할 수 있다.