Chap4 Classification

4.1 An Overview of Classification

• Classifier - 분류기

  → 회귀와 마찬가지로 분류기를 구축하는데 사용할 수 있는 train set과 test set이 존재

이 챕터의 예제

주어진 잔고(X1) 및 소득(X2) 값에 대해 부도(Y)를 예측하는 모델을 구축하는 방법

• Y가 부도 금액처럼 정량적인 값이 아니라 범주형이기 때문에 선형회귀 모델을 사용하지 않음 *

• 예제는 정확히 분류되도록 가공된 것으로 실제 사례는 명확한 분류 관계를 보여주지 않을 수 있음*

  4.2 Why Not Linear Regression

Why?

Y가 정량적인 값이 아닌 범주형이면 선형회귀를 사용하지 않을까?

Because

• 선형회귀처럼 least square를 구하면 범주형 변수들 사이에 없던 결과에 대한 순서가 생긴다.
• 자연스러운 변수들 간의 순서를 가질 때, 이를 선형 회귀 분석하면 변수별 다른 선형 모델을 생성하게 된다.

So

Y가 dummy variable 일땐, 분류 분석을 하자!

4.3 Logistic Regression

4.3.1 The Logistic Model

• 선형회귀 방식을 분류에 적용한 알고리즘 => 분류에 사용됨
• 선형인가 비선형인가는 독립변수가 아닌 가중치 변수가 선형인지 아닌지를 따름
• 선형회귀와의 차이 : 시그모이드 함수 최적선을 찾고 이 시그모이드 함수의 반환 값을 확률로 간주해 확률에 따라 분류를 결정

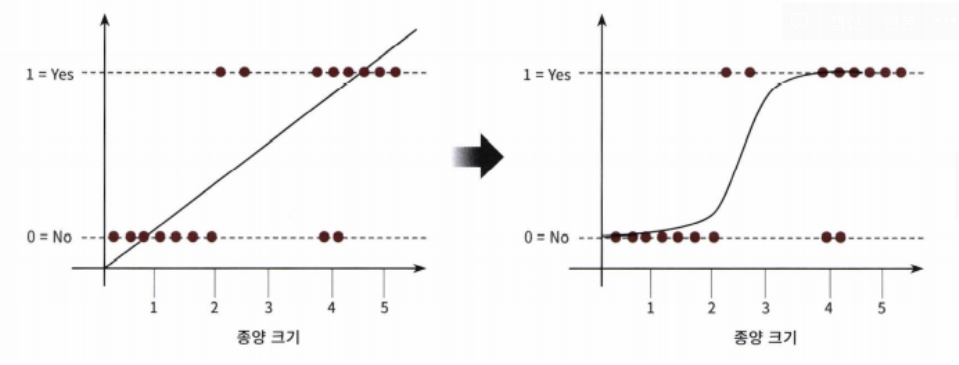
• 자연, 사회현상은 시그모이드 함수와 같이 S자 커브 형태를 가짐
• 그래프 특성상 x값이 아무리 커지거나 작아져도 y값은 항상 0과 1사이 값을 반환
  

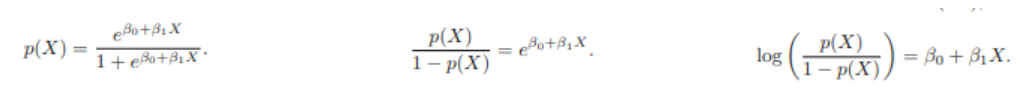
4.3.2 Estimating the Regression Coefficient

4.3.3 Making Predictions

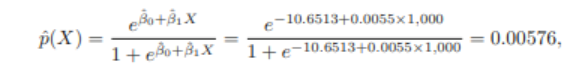
4.3.4 Multiple Logistic Regression

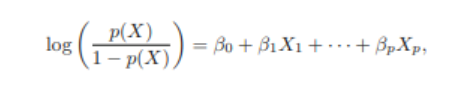
4.3.5 Logistic Regression for >2 Response Classes

두 개 이상의 클래스가 있는 응답 변수를 분류하고 싶을 땐, multiple-class extensions(다중 클래스 확장)보다는 섹션에서 배울 discriminant analysis(판별 분석)을 더 많이 사용

4.4 Linear Discriminant Analysis

• 로지스틱 회귀: 두 개의 반응변수 클래스에 대해 k에 속할 확률 Pr(Y=k|X=x)를 직접 모델링(Y의 조건부 확률 모델링)
• alternative: 반응변수 Y의 각 클래스에서 설명변수 X의 분포를 모델링(Pr(X=x|Y=k))하고, 베이즈 정리를 사용하여 Pr(Y=k|X=x)에 대해 추정
  • 만약 이 분포가 정규분포라면 로지스틱 회귀와 매우 비슷

logistic regression이 아닌 LDA를 사용하는 이유

• 범주가 명확하게 구분되어 있는 경우, 로지스틱 회귀는 불안정한 결과를 보임

• 자료의 개수가 적을 때, 각 클래스에 대한 X의 분포가 정규분포와 유사하다면, 로지스틱 회귀보다 안정적임

• 3개 이상의 범주가 있을 시 성능이 더 뛰어남

4.4.1 Using Bayes' Theorem for classification

Bayes Theorem

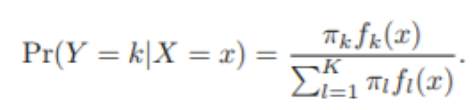
• $Pr(Y=k|X=x)$: 사후 확률
• $π_k$: 클래스 k의 사전 확률
• $fk(x)=Pr(X=x|Y=k)$: 클래스 k에서 X의 밀도함수

Bayes Classifier

: Pk(X)가 가장 큰 클래스에 할당

4.4.2 LDA for p=1

• $f_k(x)$가 정규분포를 따른다고 가정 : $X$~$N(u,sigma)$
  

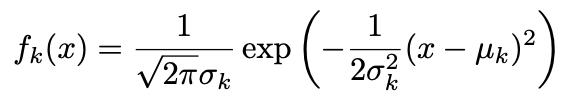
• 각 predictor는 일변량 정규분포를 따른다고 가정 $X_K$~$N(u_k,sigma)$
• k개의 클래스의 분산이 모두 동일하다고 가정

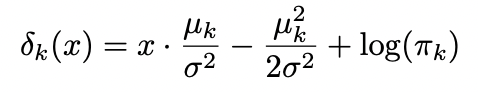
bayes classifier은 위 값이 가장 큰 클래스로 할당

but 일반적으로는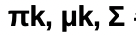
에 대한 추정이 필요함 -> 추정치를 구한 후, 위의 식에 대입함 : LDA

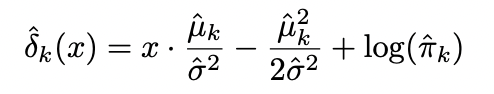
: linear function of x
LDA decision reul depends on x only through a "linear" combination of its elements

4.4.3 Linear Discriminant Analysis for p>1

LDA 방법론은 위와 동일

Traininh error rate
train set을 기반으로 모델을 학습시킴 -> train error rate 보다 test error rate 이 더 작음

Confusion Matrix
: classification 에서 실제값과 예측값을 시각화 하여 표현

ex> card default data

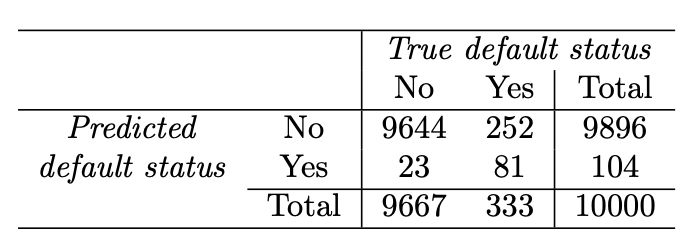
: LDA를 이용하여 분류할 경우 전체 error rate 은 낮지만, 연체자들의 분류는 75.5% 나 잘못 분류됨.

-> 단순 전체 error rate만을 accuracy의 기준으로 사용하는 것에는 무리가 있음

Sensitivity and Specificity

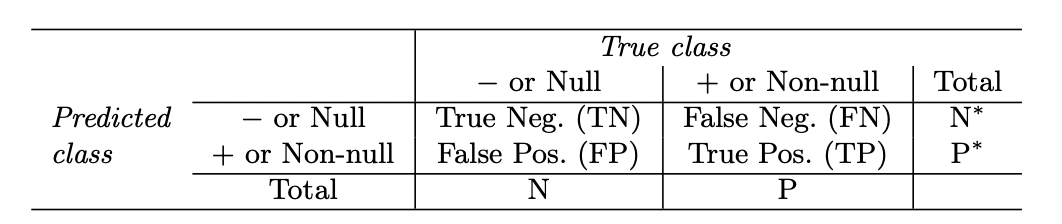
Sensitivity (민감도) : TP / (FN+TP)
실제 값이 positice인 대상 중에 예측과 실제값이 positive로 일치하는 데이터의 비율

Specificity (특이성) : TN / (TN+FP)
실제 값이 negative인 대상 중에 예측과 실제값이 negative로 일치하는 데이터의 비율

Why LDA has such sensitivity in Default data?

Default data 에서 sensitivity : 24.3%
Default data 에서 specificity : 99.8%

sensitivity -> default인 애를 default 로 얼마나 잘 분류 했는가? : card company에서 중요한 issue
but 전체 error rate은 매우 작지만, sensitivity는 좋지 않은 상황

threshold를 변화 시킴으로써 sensitivity or specificity 를 높일 수 있음.

Trade Off

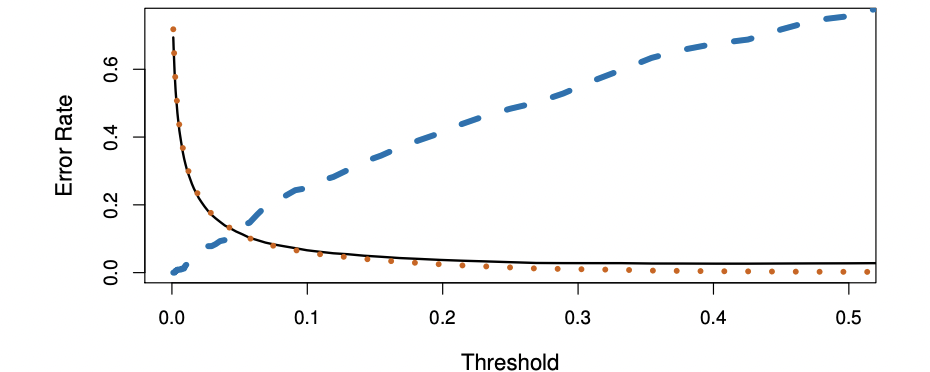
sensitivity 를 증가 시키려고 임계값을 0.2로 조정하면, 전체 error rate이 증가함 ->trade off

default data 에서는 전체 error rate이 높아지더라도, sensitivity를 줄이는 것이 중요하기 때문에 임계값을 낮출 것

threshold 의 값은 domain knowledge 에 따라 결정하면 됨.

ROC curve

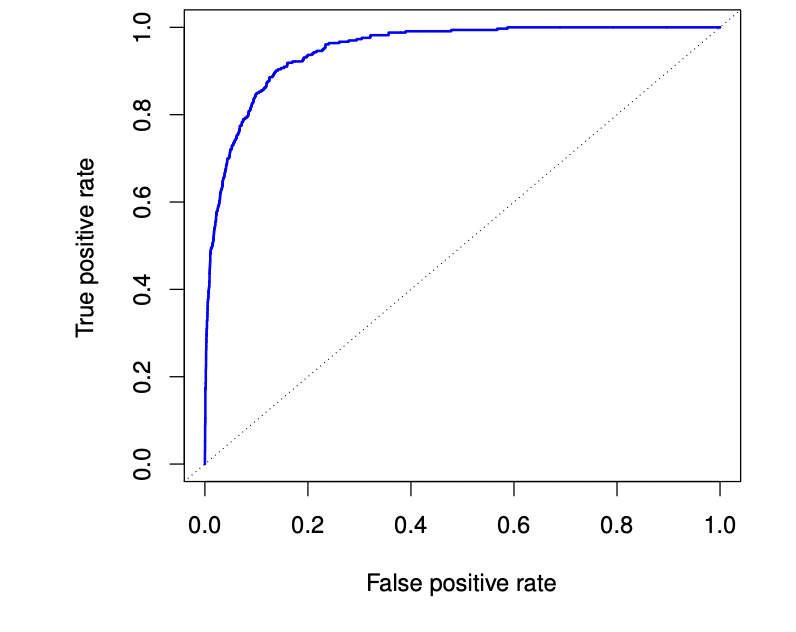
: two types of error for all possible thresholds 를 동시에 시각적으로 보여줌

• x 축 : 1- specificity
• y 축 : sensitivity
• ROC curve 아래 부분 : AUC -> 넣ㅂ을수록 좋은 분류기
• 모든 임계치를 비교하기 때문에 서로 다른 classifier 를 비교하는데 용이

4.4.4 QDA(Quadratic Discriminant Analysis)

• LDA 와 공통점

1. 각 classs 들은 모두 정규분포를 따름
2. 예측을 위해 파라미터의 추정치를 Baye's theorem에 대임

• LDA와 차이점
  각 class 들이 각각의 공분산 행렬을 가짐 (LDA 에서는 등분산가정했음)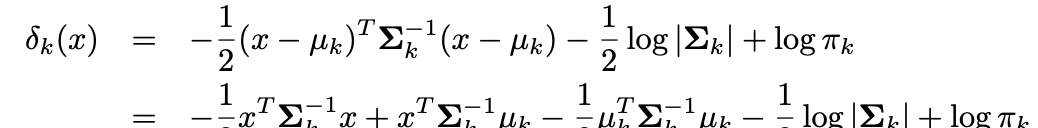

  

  위의 값이 최대가 되는 class로 예측
  위의 식 : x에 대한 quadradic fuction(not linear)

  Wht prefer LDA to QDA, or vice-versa?
  LDA : 등분산 가정해서 추정해야 될 모수의 개수 상대적으로 적음 -> variance 낮아지고 bias 높아짐 (trade off)

  : train set의 개수가 상대적으로 적어 분산을 줄이는 것이 중요한 경우 사용

  QDA : 등분산 가정 하지 않았기 때문에 추정해야할 모수의 개수 상대적으로 많음 -> variance가 높아짐

  : train set의 개수가 커서 분산을 줄이는 것이 중요하게 고려되지 않거나, k class 에 대한 공분산 행렬의 가정이 명백하게 불가능할 경우 사용

4.5 A Comparison of Classification Methods

Logistic Regression vs LDA

Logistic Regression

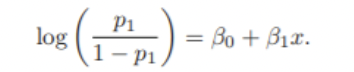
LDA

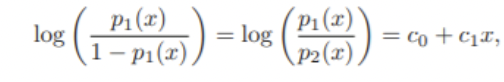
where $c_0,,c_1$ are functions of $m_1 , m_2 sigma^2$

• 공통점

1. linear functions of x
2. have linear decision boundaries

• 차이점

1. logistic regression : mle로 추정됨
2. LDA : 정규분포로부터 평균과 분산의 추정치를 갖고 계산됨

fitting하는 방법 말고는 차이가 없어 비슷한 결과를 줄 수 있지 않는가?

LDA : 데이터가 공통 공분산 행렬을 가진 가우시안 분포를 가진다는 가정이 성립하는 경우 더 선호됨

logistic regression : 정규분포 가정이 성립되지 않는 경우

KNN vs. Logistic Regression and LDA

KNN :(non-parametric) decision boundary에 대한 가정 없음 -> decision boundary가 매우 비선형일 경우 선호됨
but it does not tell us which predictors are not important

QDA vs. KNN, Logistic Regression and LDA

• knn과 Logistic Regression and LDA 사이의 절충안 역할

• Logistic Regression and LDA보다 더 넓은 범위의 문제를 다룰 수 있음

• knn처럼 flexible하지는 않지만, 학습데이터가 제한적인 경우에 decision boundary에 대한 가정이 있기 때문에 성능이 더 좋음