Chap5 Resampling Methods

서지은·2021년 11월 19일

ISLR

목록 보기

3/6

cross-validation :

model assessment : model performance를 측정하는데 사용됨
model selection 에 사용됨

bootstrap :

accuracy of a parameter를 측정하는데 주로 사용됨

5.1 Cross-Validation

test error :

model train에 사용되지 않은 new observation를 이용하여 response를 predict하고 얻은 error

계산하기 쉽지 않음 but train data를 이용하여 error를 계산한다면, 실제 test error와 다를 수 있음.

→ available training data를 이용한다면, test error를 estimate할 수 있음

how? holding out a subset of the training data observations from the fitting process

5.1.1 The validation Set Approach

validation set approach : randomly dividing the available set of observations into two parts(50%)

→ training set : 모델 fitting에 사용됨

→ validation set (hold-out set) : 이 set을 이용하여, response를 predict하고, test error를 얻음

(실제값과 prediction value의 mse를 이용함
—> estimate of the test error rate)

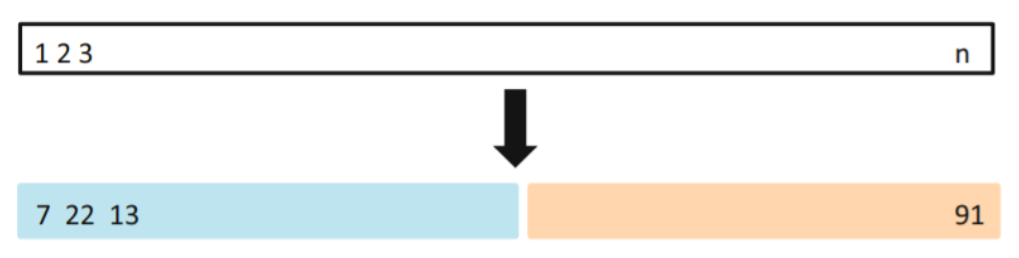
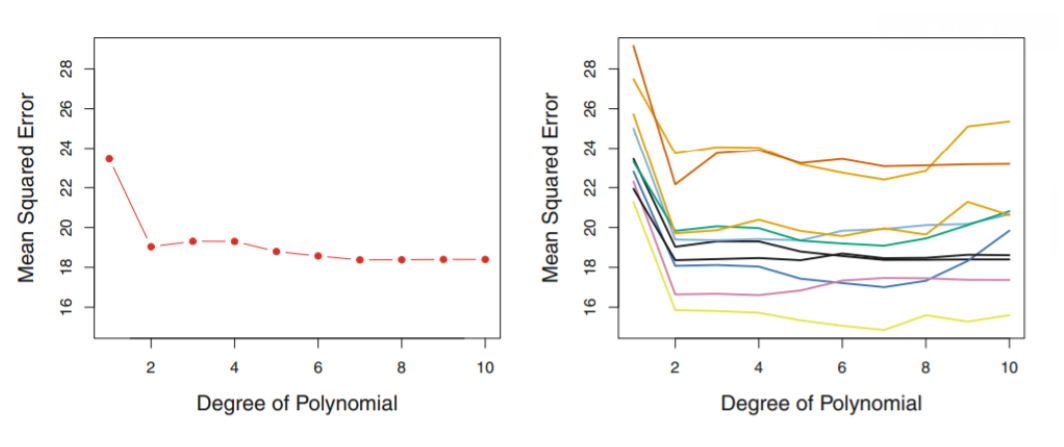
위와 같은 validation set Approach를 이용하여 test error rate을 estimate한 결과

좌측 figure :

linear model일 때보다, 2차일 때 test error가 확실하게 줄고 그 이상으로는 눈에 띄는 효과는 없음

우측 figure :

각 다른 obervation을 이용하여 test error rate을 계산해본 결과, 전반적인 추세는 비슷하지만 각 validation set에 따라 (어떤 observation이 선택되었는가) test error rate의 estimate 값에 차이가 있음

Validation set Approach의 단점 :

어떤 observation이 training set에 포함되었는가에 따라 test error rate이 달라질 수 있음
모델을 fitting 하는데 , 특정 subset만 사용됨

: observations의 수가 적으면 performace의 성능이 떨어짐 → Overestimate test error(bias)

→ 해결방안 : cross-validation

5.1.2 Leave-One-Out Cross-Validation (LOOCV)

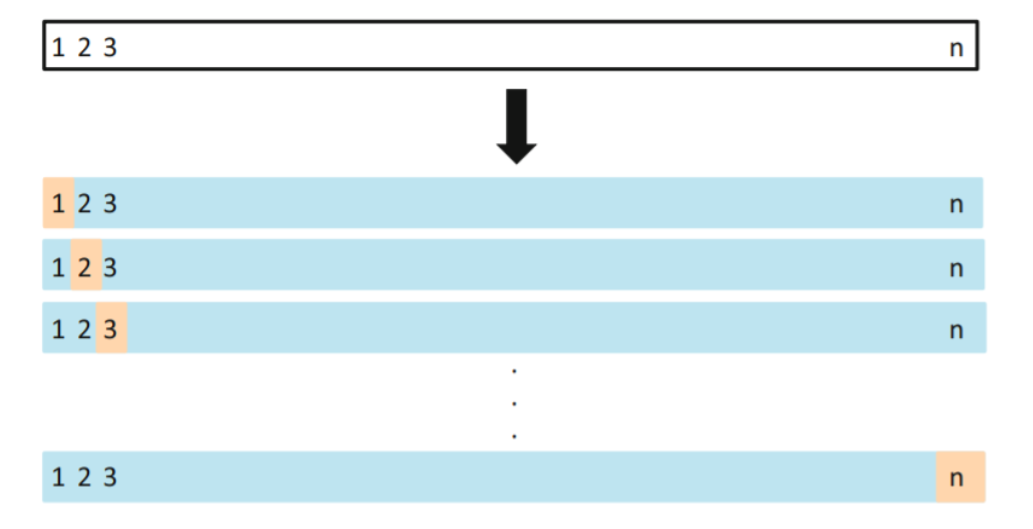
n-1개의 observation은 training data로 사용하고 나머지 하나의 observation에 대해서만 test-error estimate (MSEi)

→ 총 n개의 MSE가 나오고, 이들을 평균 낸 값을 test MSE에 대한 추정값으로 사용

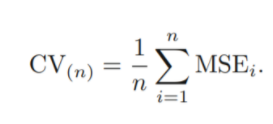
장점 >

data set 분리시 , randomness가 없기 때문에 거의 항상 비슷한 test error를 도출 (우측Figure)
less bias : n-1개의 observation(충분히 많은)을 사용하여 model fitting

→ overestimation of test error 사라짐

단점>

expensive :

n번의 fitting 필요 / 한번 모델 fitting할 때 시간이 많이 걸리는 모델이라면 더욱 많은 시간 소요됨

But 아래의 formula를 사용하면 LOOCV 접근법에 있어 계산 속도가 향상됨

LOOCV은 어떤 모델에도 적용되는 방법이지만, 아래의 formula는 항상 유효하지 는 않음.

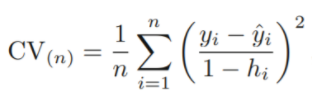
(분모 : influence of an observation이 반영됨)

5.1.3 k-fold Cross-Validation

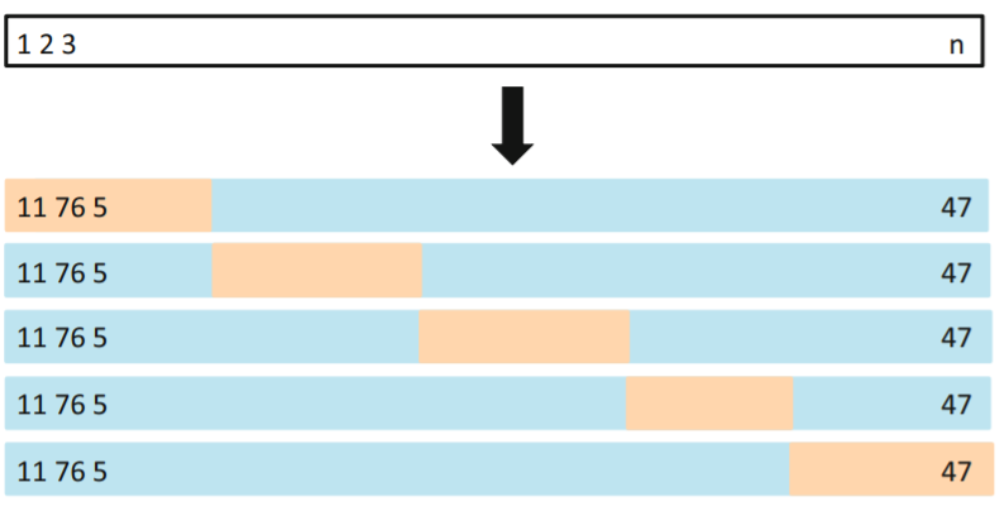
data set을 랜덤하게 k개의 gruop (=fold)으로 나누고 (단, 크기는 동일하게),

첫번째 fold는 validation set으로(hold-out Fold),
나머지는 k-1개의 fold는 train set으로 취급하여 MSE값 구하기

→ 이런 과정을 각 fold마다 k번 반복하여 k개의 MSE를 얻은 뒤, 평균을 구하여 test error estimate

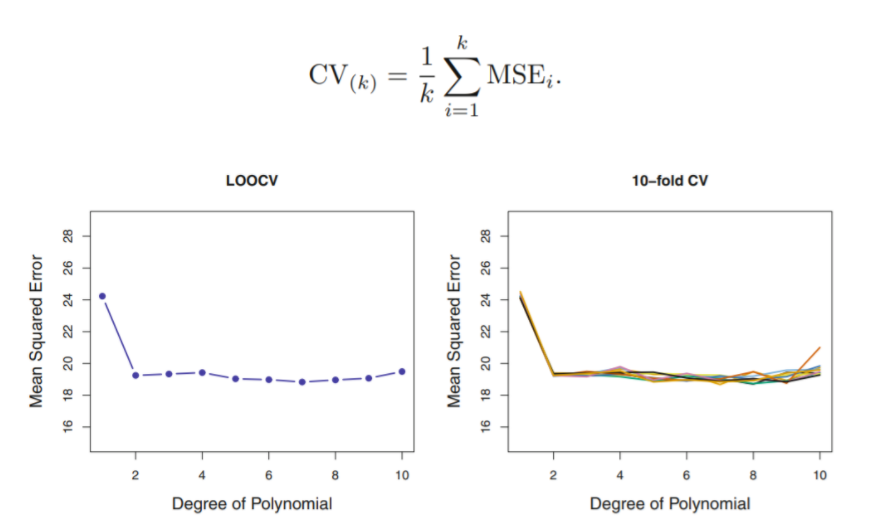
K번 반복 후, 평균을 냈기 때문에 각 추정치의 variability가 크지 않음을 그래프로 확인할 수 있음.

k번의 fitting 및 계산만 하면 되기 때문에, LOOCV보다 경제적이며,

다음장에서 다룰 Bias-Variance Trade-off 측면에서도 장점을 보임

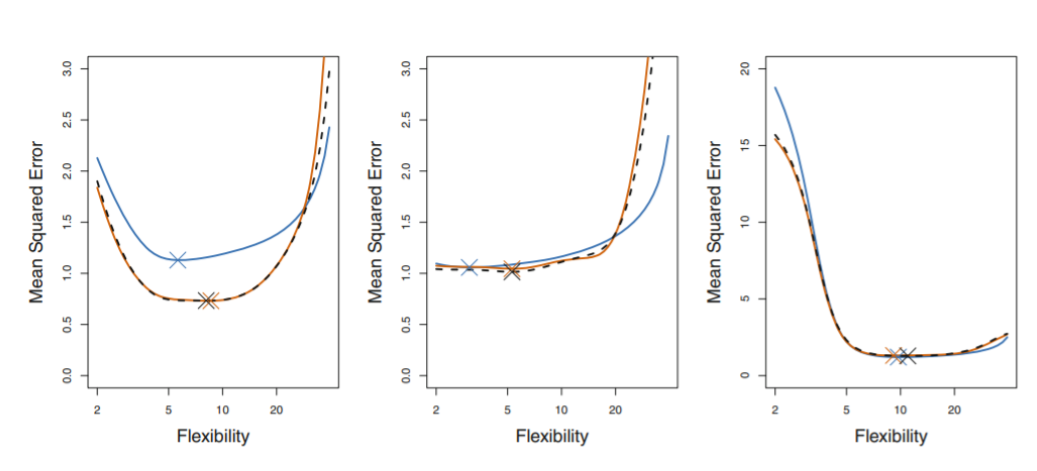
blue line : true test MSE
black line : LOOCV
orange line : 10-fold CV

test error를 정확하게 예측해내는 것도 중요하지만, 언제 test error가 min이 되는지 파악하는 것도 중요함

→ 이러한 관점에서, 맨 왼쪽 LOOCV , 10-fold CV 는 test error을 underestimate했지만 minimum point를 잡아냈다는 점에서는 의미가 있음.

5.1.4 Bias-Variance Trade-Off for k-fold Cross-validation

(LOOCV보다) K-fold 가 가지는 장점

계산 측면에서의 경제성
more accurate (Bias-Variance Trade-Off)

bias reduction 측면에서는 LOOCV가 k-fold보다 더 유리함.

(각 training set이 n-1개의 observation이 있기 때문 : 충분히 많은 observation)

samll variance (추정치의) 또한 무시할 수 없는 지표임

k-fold가 LOOCV보다 lower variance를 가짐 (accurate estimates of the test error)

why? LOOCV에서는 비슷한 데이터를 가지고 n번 fitting 해서 결과를 얻은 후 평균을 냉

→ 이 결과들은 correlation이 높으며, correlation이 높은 quantities들의 평균은 higher variance를 가짐.
→ k-fold에서는 이보다 덜 correlated 되어있고 따라서 lower variance를 가짐.
→ k가 n에 가까워지면 , bias는 작아지지만 variance는 커지고

k 가 1에 가까워지면 variance는 작아지지만 bias는 커짐
: bias - variance Trade Off

bias와 variance가 적절한 균형을 이루는 k의 값이 5 or 10이라는 사실이 경험적으로 알려져있음.

5.1.5 Cross-Validation on Classification Problems

Regression : test error의 quantify로 MSE 사용

Classification : test error의 척도로 the number of misclassified obervations를 사용(Err)

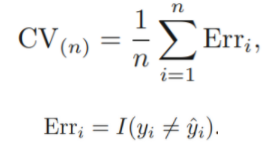
ex> logistic regression

black solid line : estimated decision boundary

test data의 값을 알고 있는 상황에서,
변수의 degree(차수)별 test error는 순서대로 0.201 , 0.197 , 0.160 , 0.162 이다.

(Bayes error rate : 0.133)

cf > Bayes error rate :

Training data를 완벽히 학습하였을 때, 그 Training data에 대해 가장 확률이 높은 Class Label을 선택하는 방법에서 발생하는 이론적 최소 오차. (즉, 달성할 수 있는 가장 낮은 예측 오차)

teste error는 계속 감소하다가 degree3->4로 넘어갈 때 증가하므로, degree3인 모델 선택이 합리적

but, Actual data에서 실제 test error 및 Bayes error rate을 모르는 상황에서는 어떤 결정을 내려야 하는가? → k-fold활용

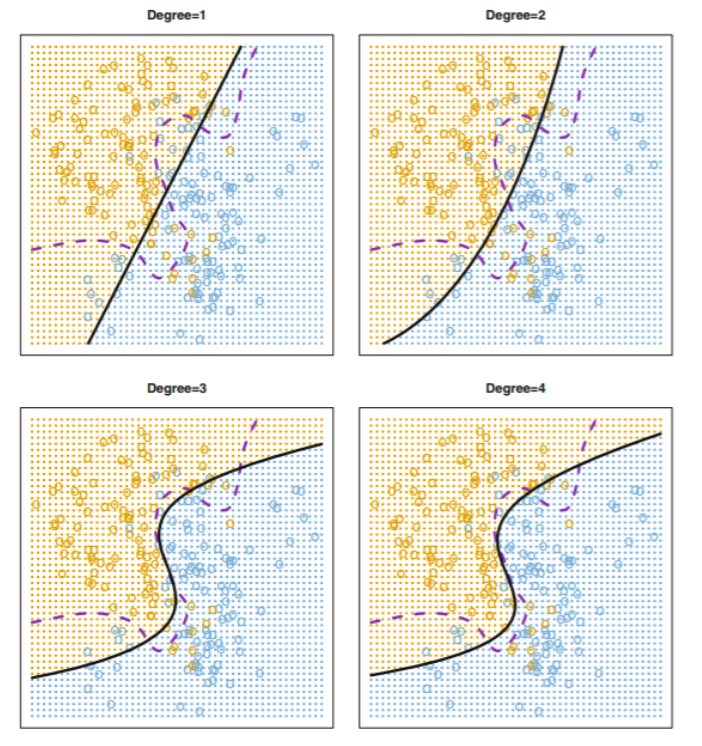
<좌측 figure>

blue line : training errors → 계속 감소함

brown line : true test errors → 감소하다가 증가하는 U-shape을 가짐

black line : k-fold errors → true test error를 underestimate하지만 꽤 잘 예측해냄.

→ minimum point 가 degree=4일 때 임을 꽤 잘 보여줌

따라서, fourth-order polynomials를 이용하면 good test performance를 보여줄 것임.

<우측 figure>

KNN approach for classification

위와 비슷한 결과를 보임

5.2 Bootstrap

given estimator 또는 statistical learning method 의 uncertainty 를 나타낼 때 중요하게 사용됨

ex> estimate the standard errors of the coefficients

장점 > variability를 얻기 어려운, statistical learning method에도 적용할 수 있음

(wide range of statistical learning method에 적용 가능함)

Example> simulation 을 이용한 추정 (from true population)

제한된 자본을 가지고 가장 Risk가 적도록 return이 X인 곳에 a 만큼 ,return이 Y인곳 1-a만큼 투자하고 싶음

이 값들의 추정을 위해 simulation을 사용하자.

아래의 그림은 각 X,Y(return)을 100 pairs씩 simulation한 4개의 그림이고,

alpha의 추정치는 0.532 - 0.657의 범위를 가진다.

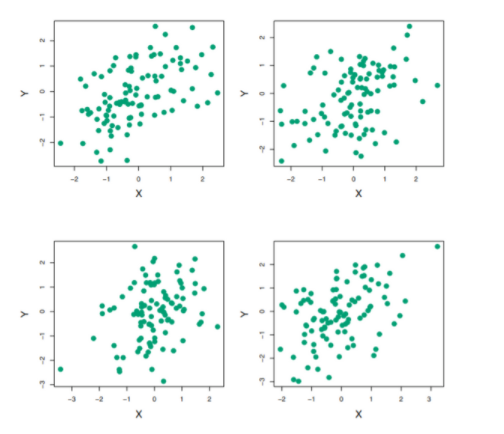
alpha를 더 정확히 추정하기 위해, 1000번 simulation한뒤, 얻은 alpha 추정치의 평균을 구해보자.

→ simulation을 이용하면 위와 같이 거의 정확한 추정치를 얻을 수 있음. 하지만, 매번 new sample을 얻는 것은 true population을 모르면 불가능한 일임.

→ boostrap을 이용하면 additional samples을 generating 하는 대신 , original data set에서 반복적으로 distinct한 sample을 얻을 수 있고 이를 이용해 추정치를 얻을 수 있다.

Boostrap :

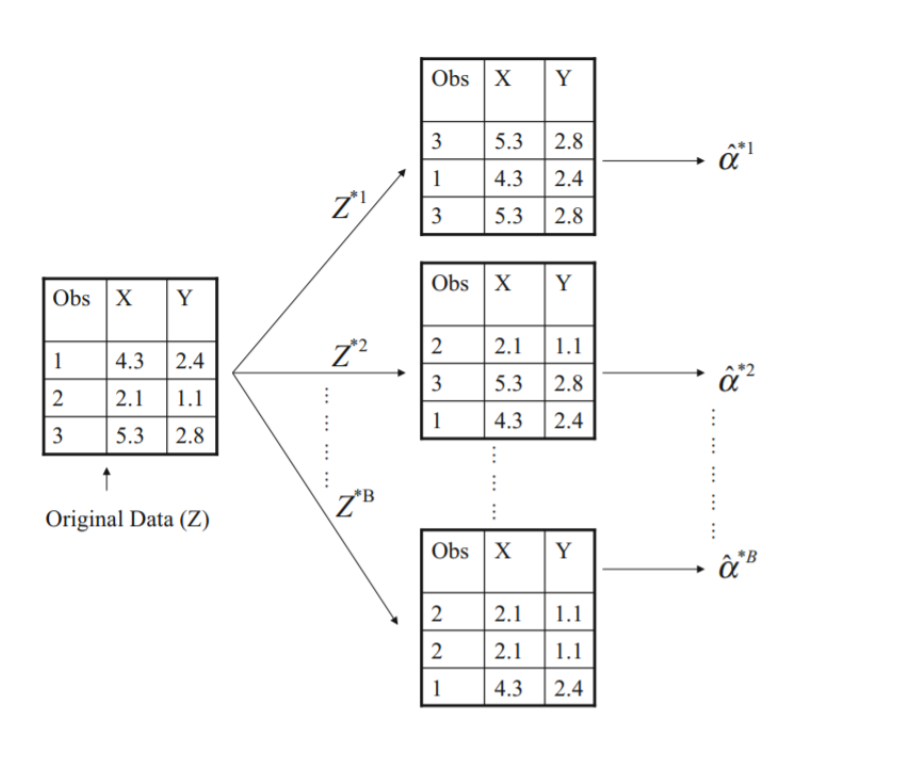
sampling은 with replacement로 얻어짐.

n=3개인 data set에서 with replacement로 sampling하면 single data set에서 총 27개의 distinct한 data set을 얻을 수 있고, 각 data set에서 alpha를 추정하면 이의 Standard Error값을 얻을 수 있다.

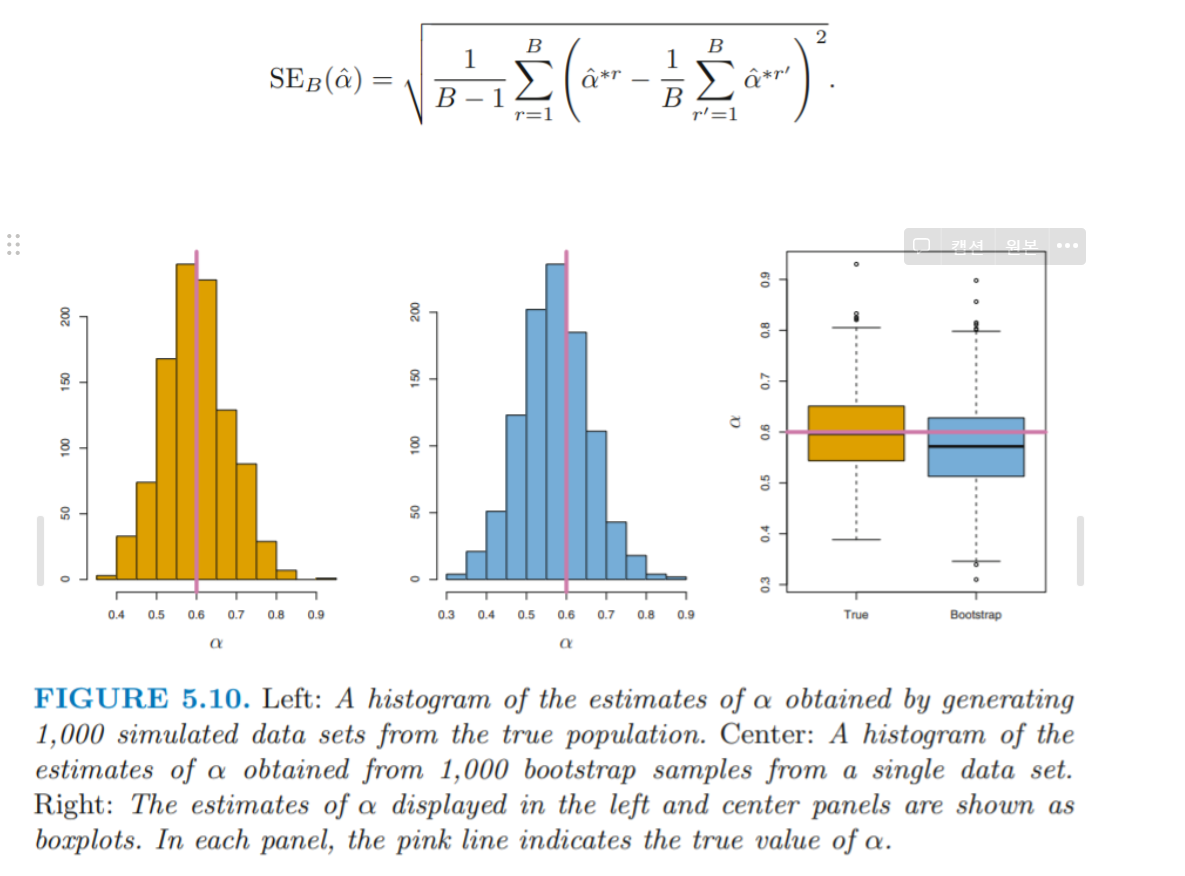
orange: simulation from true population