210824-25 CodeStates 27-28일차
210824-25 CodeStates 27-28일차
이틀간 재귀에 대하여 학습했다.
재귀의 의미에 대해 알아보고 재귀의 개념을 이용해 코플릿문제들을 풀었고 tree UI를 만들어보는 실습을 진행했다.
다른 언어를 배울때도 재귀에 대한 개념은 알고있었지만 잘 사용하지는 못했다. (무한루프 ㅠㅠ....)
개념에 대해 정확히 이해하려고 노력했고 여러번 사용을 해본 결과 전보다는 재귀를 사용하는데에 익숙해진 것 같다.
프로그래머스의 문제들을 풀때에도 응용해보려는 시도를 하며 점점 능숙하게 사용할 수 있어야 할 듯하다.
재귀
재귀란 어떤 문제를 해결할 때, 동일한 구조의 더 작은 문제를 해결함으로써 주어진 문제를 해결하는 방법이다.
자바스크립트에서 함수를 실행할 때, 실행과정 중에 자기자신(함수)를 호출하는 방식을 재귀호출이라 하며 함수가 종료되기전에 자기자신을 재귀호출하는 함수를 재귀함수라고 한다.
재귀를 이용한다는 것은 문제를 더 작은 동일한 문제를 나누어 해결하는 것과 같기 때문에 반복문을 이용해서도 표현할 수도 있다.
하지만 중첩된 반복문이 너무 많거나 혹은 너무 많은 나머지 중첩횟수를 예측하기 어려운 경우에는 재귀함수를 이용하여 문제를 해결하는 방법이 바람직할것이다.
재귀함수를 이용하여 피보나치수 구하기
재귀적으로 사고하여 피보나치수를 구하는 함수를 작성해보자.
피보나치수열이란 0번째항과 1번째항이 1로 시작하며 그 뒤의 모든 항은 바로 앞 두항의 합인 수열을 말한다.
ex) 1 1 2 3 5 8 13 .......
-
재귀함수를 이용하기 위해서는 먼저 재귀함수의 입력값과 출력값을 정의해야한다.
재귀함수를 통해 풀고자 하는 문제, 도달해야하는 목표를 정의한다.
어떤 값을 함수의 인자로 받아야하고, 어떤 값을 리턴해야 할지에 대한 생각을 정리해야 한다.피보나치수를 구하는 함수를 만들기 위해 num이라는 숫자를 인자로 받아 num번째 피보나치 수를 리턴하는 함수를 작성해야 한다.
function fibonacci(num){ ... } //num번째 피보나치수를 반환하는 함수 -
문제를 더 작은 동일한 문제로 쪼개고 경우의 수를 생각한다.
주어진 문제를 어떻게 동일한 더 작은 문제로 쪼갤 것인지를 고민한다.
일반적인 경우 작은 문제로 쪼갤때 입력값을 기준으로 경우의 수를 생각하게 된다.일반적인 경우에는 num번째 피보나치수를 계산하여 반환하기 위해서 num-1번째 피보나치수와 num-2번째 피보나치 수를 계산하여 더해줘야한다.
num이 0또는 1인 특수한 경우에는 미리 정의되어 있는 피보나치수열의 0번째,1번째항의 값인 1을 리턴해야 할 것이다.num이 0또는 1인경우, 더 이상 문제를 쪼갤 수 없을 때 1이라는 답을 리턴하게 된다.
답을 리턴한다는 것은 더 이상 재귀함수를 호출하지 않고 종료할 수 있다는 의미이며 이러한 종료조건을 BaseCase라고 한다.
일반적인 경우에는 복잡한 문제(num번째 피보나치 수를 구하는)를 더 간단한 문제(num-1번째,num-2번째 피보나치수를 구하는)로 나누어 피보나치수를 구하는 함수 자기자신을 호출하게 된다.
이를 Recursion Case라고 한다.
-
Base Case와 Recursion Case를 정리하여 코드로 구현한다.
function fibonacci(num){ if(num===0||num===1){ return 1; } //Base Case return fibonacci(num-1)+fibonacci(num-2); //Recursion Case }
메모제이션을 이용하여 불필요한 계산 줄이기
피보나치 수를 구하는 함수를 조금 더 살펴보자.
5번째 피보나치수를 구하기 위해 fibonacci(5)를 실행하게 되고 해당 함수는 fibonacci(4)와 fibonacci(3)을 호출하게 된다.
연쇄적으로 fibonacci함수를 호출하는 과정을 거치며 num이 0또는 1이 되어 1을 리턴하기까지 15번 fibonacci함수를 호출하게 된다.
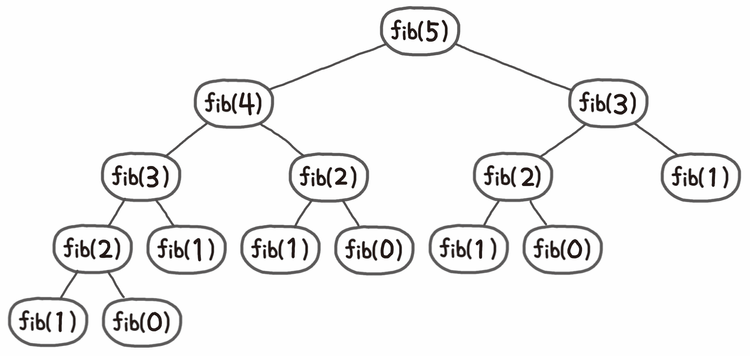
fibonacci(0)을 3번, fibonacci(1)을 5번, fibonacci(2)을 3번, fibonacci(3)을 2번 호출하며 같은 계산을 불필요하게 여러번 처리하게 된다.
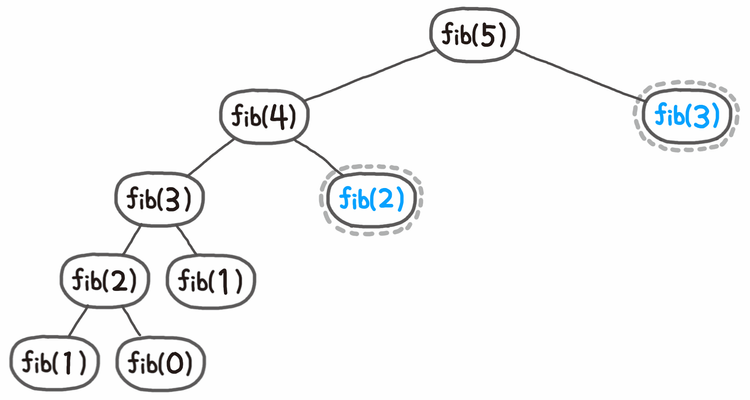
동일한 계산을 반복해야 할 경우, 한번 계산한 결과를 메모리에 저장해 두었다가 꺼내씀으로써 중복된 계산을 방지하는 메모제이션 기법을 이용하여 불필요한 계산을 줄일 수 있다.
function fibonacci(num,list){
if(list[num]===undefined){
list[num]=fibonacci(num-1,list)+fibonacci(num-2,list);
}
return list[num];
}
console.log(fibonacci(5,[1,1]);
// 8매개변수 list의 num번째 인덱스에 num번째 피보나치수를 계산하여 넣어주면 해당 피보나치수를 다시 계산할 필요없이 list의 num번째 요소를 반환하면 된다.
재귀를 이용하여 하노이탑 문제풀어보기
재귀를 이용하여 프로그래머스의 하노이탑문제를 풀어보자.
대학에서 이산수학이라는 과목을 수강할 때 점화식을 배우면서 하노이 탑문제를 접해봤다.
문제에서 말하는대로 1번 기둥에서 3번 기둥으로 n개의 원판을 옮기기 위해서는
- 3개의 기둥중 시작과 끝을 제외한 나머지 기둥(2번 기둥)에 먼저 n-1개의 원판을 옮긴다.
- 제일 큰 n번 원판을 1번 기둥에서 3번 기둥으로 옮긴다.
- 2번 기둥에 옮겨놓았던 n-1대의 원판을 3번 기둥의 n번 원판위에 옮긴다.
의 과정을 거치면 된다.
2번째 과정을 제외한 1,3번째 과정은 상당히 유사하며 해결해야 하는 문제와 동일한 더 작은 문제라는 생각이 든다.
문제를 해결하기 위해 n개의 원판을 시작지점에서 도착지점까지 옮기며 그 과정을 기록할 배열에 기록하는 함수를 만들어야 할것 같다.
function move(n,start,end,list){
...
}만약에 옮겨야하는 원판의 갯수가 1이라면 더 이상 작은 문제로 나눌수 없는 Base Case가 될 것이며, 배열에 하나의 원판을 옮기는 과정을 기록해야 할 것 같다.
그외의 일반적인 경우에는 위의 3단계의 과정을 진행해야 할 것 같다.(Recursion Case)
이렇게 Base Case와 Recursion Case를 정리한 후 코드로 구현해보았다.
function move(n,start,end,list){
if(n===1){
list.push([start,end]);
}
//Base Case
else{
let middle=[1,2,3].filter(el => el!==start && el!==end)[0];
//middle: 시작과 끝을 제외한 나머지 기둥
move(n-1,start,middle,list);
//1단계: n-1개의 원판을 나머지 기둥에 옮긴다.
list.push([start,end]);
//2단계: 가장 큰 n번 원판을 시작지점에서 도착지점으로 옮긴다.
move(n-1,middle,end,list);
//3단계: 나머지 기둥에 옮겼던 n-1개의 원판을 도착지점에 옮긴다.
}
//Recursion Case
}
function solution(n){
let answer=[];
move(n,1,3,answer);
return answer;
}재귀를 익숙하게 사용하기 위해서는 더 많은 문제를 풀어봐야 할 것 같다.