210826-27 CodeStates 29-30일차

공윤배·2021년 9월 5일

210826-27 CodeStates 29-30일차

이틀간 Stack,Queue,Tree,Graph의 자료구조와 트리의 순회, 그래프의 탐색에 대해 개념을 배우고 코플릿의 문제들을 풀었다.
자료구조의 개념은 정보처리기사를 준비하면서 공부했던 적이 있지만 이를 자바스크립트의 코드로 구현해보는 것은 처음이고, 생각보다 쉽지 않았다.
앞으로 문제를 풀때 적극적으로 적합한 자료구조와 탐색기법이 무엇인지 생각해보고 이용해봐야 할 것 같다.

자료구조란?

자료구조란 여러 데이터들의 묶음을 저장하고 사용하는 방법을 정의한 것이다.
데이터를 정해진 규칙없이 저장하거나, 하나의 구조로만 정리하고 활용하는 것보다 체계적으로 정리하여 저장해두는게, 데이터를 활용하는데 훨씬 유리할 것이다.
앞으로 문제를 풀면서 다양한 상황을 마주하게 될 것이고, 데이터를 효율적으로 다룰 수 있는 방법인 자료구조를 상황에 적절하게 사용한다면 문제를 쉽

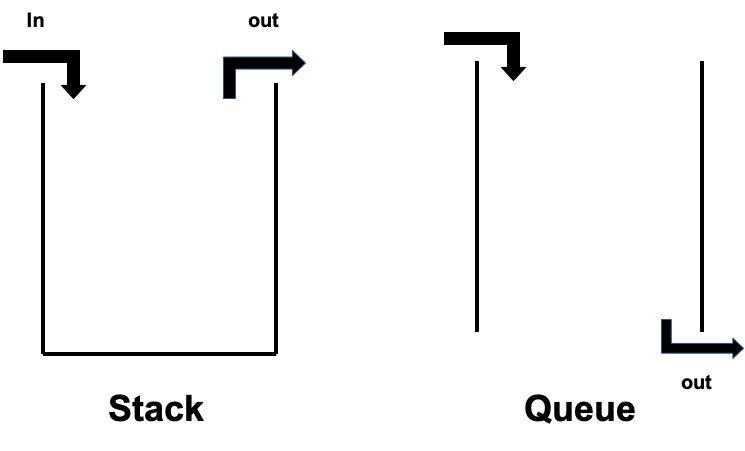
Stack

Stack은 쌓다,쌓이다 라는 의미를 가진 단어이다.
단어의 의미와 비슷하게 데이터를 순서대로 쌓는 자료구조이다.
Stack의 특징은 입력과 출력이 한 방향에서 이루어지며 먼저 들어온 데이터가 나중에 들어온 데이터의 밑에 쌓이기 때문에 처음들어온 데이터가 제일 마지막에 출력된다.(FILO First In Last Out)
브라우저의 앞으로가기, 뒤로가기 기능을 구현할 때 스택의 자료구조가 사용된다.

Queue

Queue는 줄을 서다,대기행렬 이라는 의미를 가진 단어이다.
단어의 의미와 비슷하게 데이터를 순서대로 줄을 세운다.
Queue의 특징은 데이터를 쌓는 Stack과는 다르게 줄을 세우기 때문에 먼저 들어온 데이터가 먼저 출력된다.(FIFO First In First Out)
프린트의 인쇄 대기열에 큐의 자료구조가 사용된다.
(먼저 인쇄명령을 내린 문서가 먼저 출력된다.)
스택과 큐

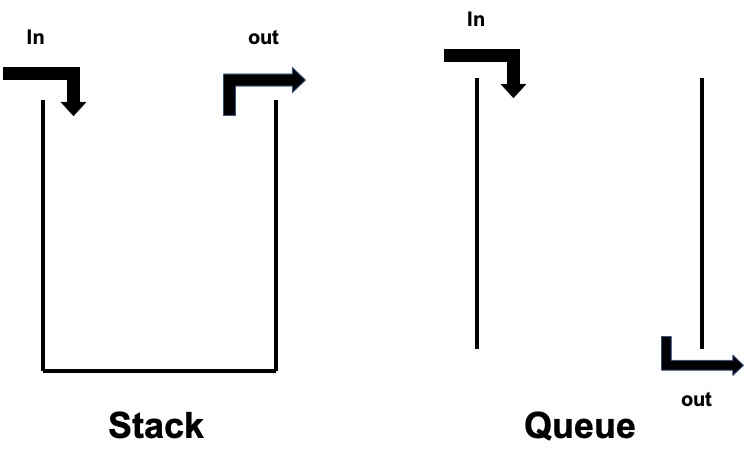
Graph

Graph는 여러개의 점이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조이다.
하나의 점을 정점(vertex)라하고, 정점간을 연결시켜주는 선을 간선(edge)라고 한다.

그래프에 관련된 여러가지 용어

진입차수/진출차수: 한 정점에 대해 다른 정점으로 들어오는 간선의 갯수를 진입차수, 해당 정점에서 다른 정점으로 나가는 간선의 갯수를 진출차수라고 한다.
인접: 두 정점간에 간선으로 연결되어 있다면 두 정점은 '인접'해 있다고 한다.
사이클: 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다.

그래프는 인접행렬과 인접리스트를 이용하여 표현할 수 있다.
인접행렬은 정점들의 인접여부를 2차원 배열의 형태로 나타낸 행렬(matrix)이다.
인접해 있다면 1, 인접하지 않는다면 0으로 표현한다.
인접리스트는 각각의 정점들이 인접한 정점들을 리스트로 나타내어 표현한다.
각 정점마다 하나의 리스트를 가지며, 리스트는 해당 정점과 인접한 다른 정점들을 담고있다.

Data Structure Visualization에서 데이터의 구조를 시각적으로 확인할 수 있다.

Tree

Tree는 단어의 의미 그대로 나무를 거꾸로 뒤집어 놓은 형태를 가지고 있다.
하나의 Root노드(뿌리)로부터 가지가 사방으로 뻗은 형태가 나무와 닮았다고 하여 트리구조라 부른다.
트리구조는 저장된 데이터를 노드라고 하며, 하나의 노드는 여러개의 자식노드를 가질 수 있으며 단방향으로 연결되어 있기에 사이클이 존재하지 않는다.
두개의 노드가 상하계층으로 연결되어 있다면 두 노드는 부모/자식의 관계를 갖는다.

트리에 관련된 여러가지 용어

노드: 트리구조를 이루는 모든 개별 데이터
루트: 트리구조의 시작점이 되는 노드
부모노드: 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에 가까운 노드
자식노드: 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에서 먼 노드
리프노드: 트리구조의 끝지점, 자식노드가 없는 노드

컴퓨터의 디렉토리 구조는 대표적인 트리구조의 예제이다.

Binary Search Tree

Binary Tree는 트리를 이루는 모든 노드들이 가질 수 있는 최대 자식노드의 수가 2인 트리구조이다.
2개의 자식노드는 왼쪽 자식노드와 오른쪽 자식노드로 구분할 수 있다.
Binary Search Tree는 Binary Tree의 자식노드중 왼쪽 자식노드의 값은 부모노드의 값보다 작고 오른쪽 자식노드의 값은 부모노드의 값보다 큰 특징을 가지는 효율적인 탐색을 가능하게 해주는 트리구조이다.

트리의 순회

특정 목적을 위해 트리의 모든 노드를 한번씩 방문하는 것을 트리순회라고 한다.
다음은 트리의 순회방법중 전위순회(preorder),중위순회(inorder),후위순회(postorder)에 대한 설명이다.

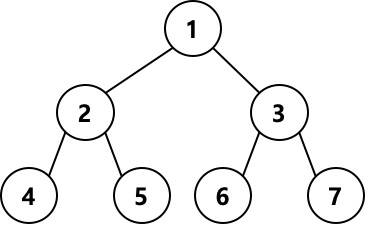
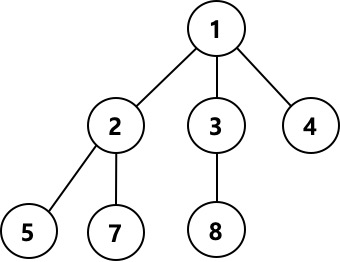
전위순회(preoreder)
이진트리에서 Root-Left-Right순으로 노드를 순회한다.
위와 같은 트리구조에서는 전위순회로 노드를 순회할때 1-2-4-5-3-6-7의 순으로 순회하게 된다.
중위순회(inorder)
이진트리에서 Left-Root-Right의 순으로 노드를 순회한다.
위의 트리구조에서 중위순회로 노드를 순회할때 4-2-5-1-6-3-7의 순으로 순회하게 된다.
후위순회(postorder)
이진트리에서 Left-Right-Root순으로 노드를 순회한다.
위의 트리구조에서는 후위순회로 노드를 순회할때 4-5-2-6-7-3-1의 순으로 순회하게 된다.

그래프 탐색

그래프를 탐색할 때에는 하나의 정점에서 시작하여 모든 정점들을 한번씩 방문하는 것이 목적이다.
특정 도시에서 다른 도시로 이동할 수 있는지의 여부, 전자회로에서 특정 단자와 원하는 다른 단자가 연결되어있는지의 여부등을 알아보기 위해서는 그래프를 생성하고 정점간의 연결된 경로가 있는지 확인해야한다.
그래프는 배열처럼 정렬되어 있는 데이터가 아니기 때문에 모든 정점들을 하나씩 방문하여 원하는 데이터(원하는 목적지)를 찾아야한다.
그래프의 모든 정점을 탐색하는 그래프 탐색의 대표적인 방법 두가지가 BFS와 DFS이다.

BFS(Breadth-First Search)
너비우선탐색이라고도 불린다.
BFS는 시작정점에서 시작하여 인접한 정점을 먼저 탐색하는 방법이다.
시작정점에서 가까운 정점을 먼저 방문하고 단계적으로 멀리 떨어진 정점을 탐색하며 깊게 탐색하기보다는 넓이를 우선적으로 탐색한다.
DFS(Depth-First Search)
깊이우선탐색이라고도 불린다.
DFS는 시작정점에서 시작하여 인접한 정점이 여러개일 경우 한 정점에 대해 연결된 모든 정점을 탐색한후 다음 인접정점을 탐색하는 방법이다.
한방향으로 깊게 탐색하다가 더 이상 탐색할 수 없을때 갈림길로 되돌아와 다음방향으로 탐색하는 방법이다.

BFS와 DFS는 깊이를 우선하는가(DFS), 넓이를 우선하는가(BFS)의 차이가 있다.
두가지 탐색법 모두 사용할 때에는 이전에 탐색했던 정점을 다시 탐색하지 않도록 기록해두어야한다.
그렇지 않다면 사이클이 존재하는 그래프의 경우 무한루프에 빠질수 있다.

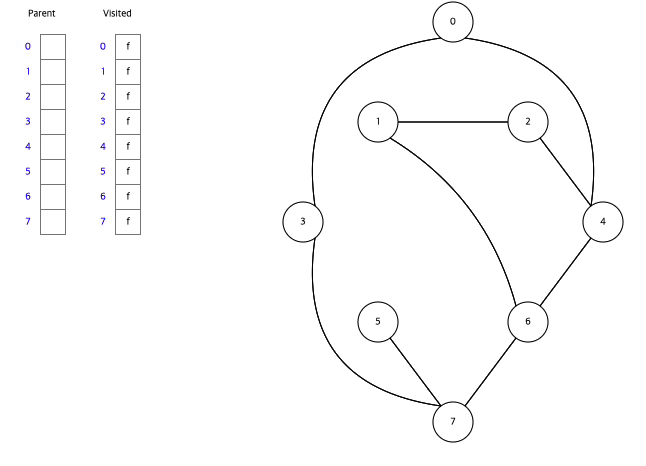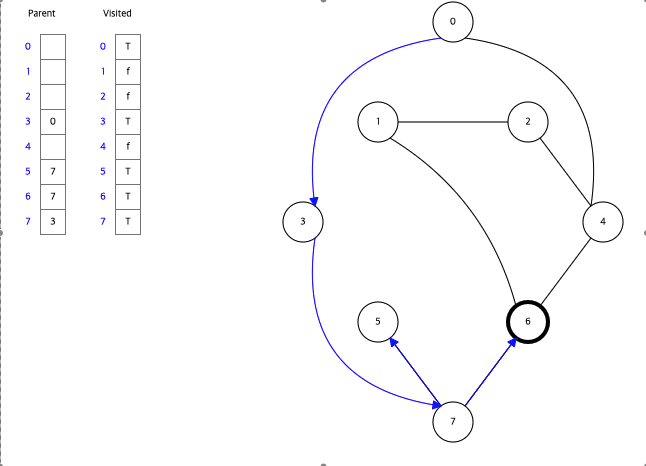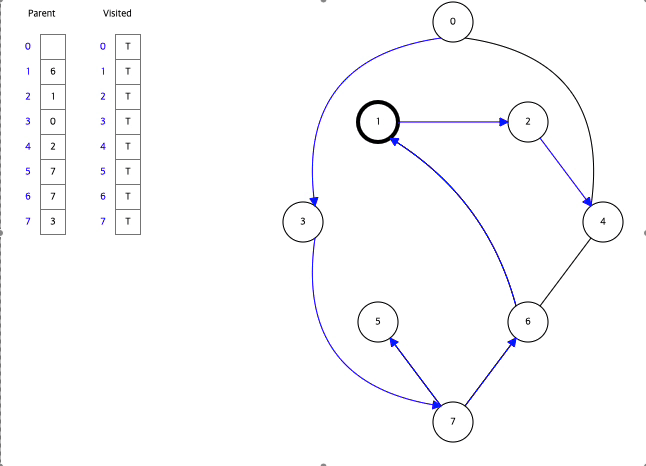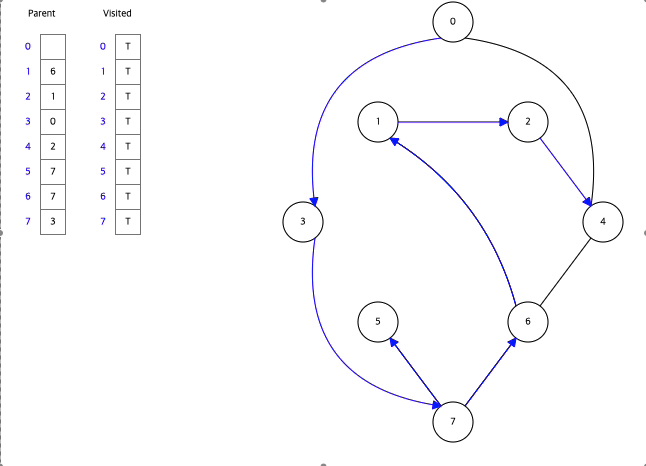
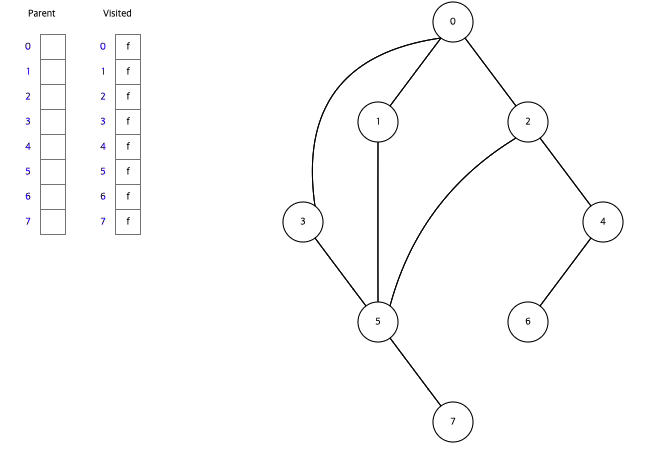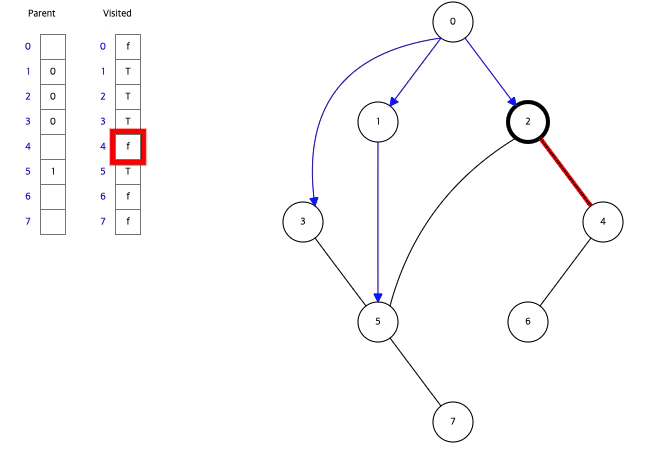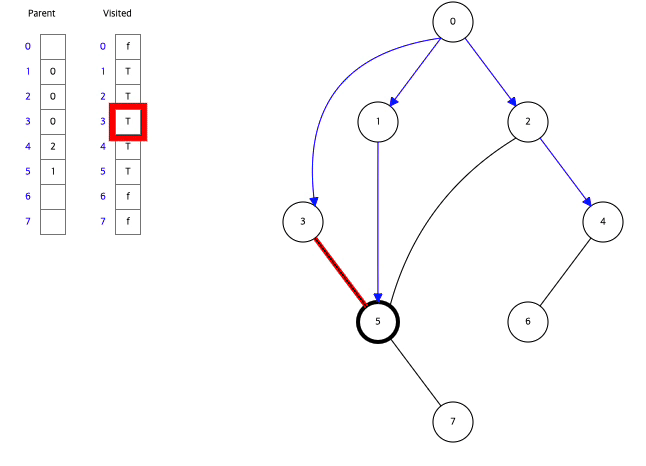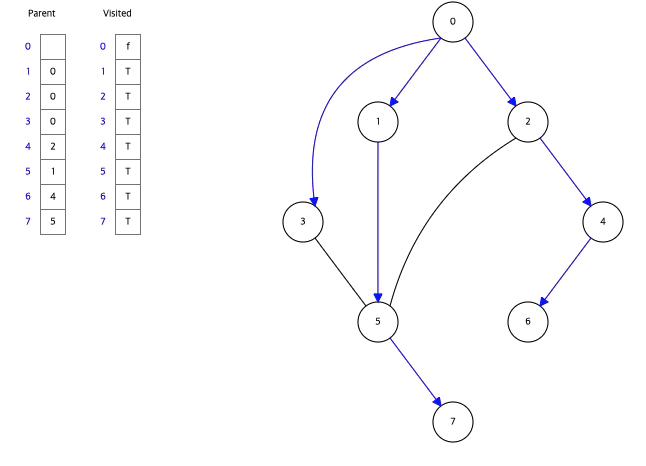
아래는 Data Structure Visualization에서 직접 BFS와 DFS를 실행한 모습이다.
BFS,DFS둘다 Visited라는 배열을 활용하여 한번 탐색한 정점을 다시 탐색하지 않으면서 탐색하고 있음을 알수있다.