CS50_4.알고리즘

본 포스트는 boostcourse의 '모두를 위한 컴퓨터 과학 (CS50 2019)'를 바탕으로 작성되었습니다.

검색 알고리즘

어떤 배열 안에 내가 원하는 값이 있는지 알고 싶을 때 이를 찾기 위한 방법은 다양할 것이다.

예를 들어, 숫자가 들어있는 7개의 사물함이 있다. '9'가 어느 사물함에 들어있는지 찾고싶다면 처음부터 끝까지(9를 찾을 때까지) 사물함을 열어볼 것이다. 이를 선형 검색이라고 한다.

• 선형 검색 (Linear Search)
  : 배열의 인덱스를 처음부터 끝까지 하나씩 증가시키면서 방문하여 원하는 값인지 검사한다. 선형 검색의 의사코드는 아래와 같다.

For i from 0 to n–1

    If i'th element is 9

    Return true

Return false

그런데 이때 만약 사물함 안에 있는 숫자가 작은 수부터 순서대로 들어있다면 처음부터 열어보는 것은 비효율적일 것이다.

가운데 사물함을 열어보고 9보다 작은 수가 있다면 그 전 사물함 중 가운데를, 9보다 큰 수가 있다면 그 후 사물함 중 가운데를 열어보면 된다.

이를 반복하다보면 9를 더 빠르게 찾을 수 있을 것이다. 이를 이진 검색이라고 한다.

• 이진 검색 (Binary Search)
  : 배열이 정렬되어 있다면, 배열 중간 인덱스부터 시작하여 찾고자 하는 값과 비교하며 그보다 작은 값이 저장되어 있는 인덱스 혹은 큰 값이 저장된 인덱스로 이동을 반복한다. 배열을 계속해서 절반으로 나누어 보는 것이다.

If no items

    Return false

If middle item is 9

    Return true

Else if 9 < middle item

    Search left half

Else if 9 > middle item

    Search right half

언뜻 보면 두 방법 중 이진 검색이 무조건 효율적일 것 같지만 이진 검색은 배열이 반드시 정렬되어 있어야 한다.

그렇기 때문에 정렬하는데 시간이 오래 걸리는 배열이라면 선형 검색이 더 좋을 수도 있다. 그런데, 만약 값을 여러 개 찾아야한다면 오래 걸리더라도 한 번 정렬을 먼저 하고 찾는 것이 장기적으로 이득일 것이다.

이렇듯 절대적으로 효율적인 것은 없으니 상황에 따라 맞는 방법을 고민하고 선택해야 한다.

알고리즘 표기법

알고리즘의 효율성을 표현하기 위해 프로그램이나 알고리즘의 실행 시간의 상한과 하한을 표기하는 방법이 있다.

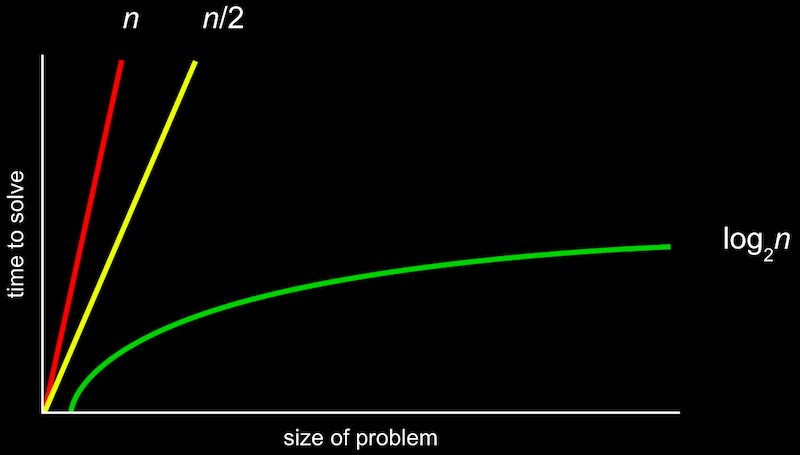
Big O 표기법
알고리즘 실행시간의 상한을 나타낸 것으로, O는 on the order of(~만큼의 정도로 커지는)의 약자이다.

여기서 유의할 점은 수식에서 가장 영향력 있는 항 외 나머지를 제거하여 표기하는 점근적 표기법이라는 것이다.

알고리즘의 실행시간에서 중요한 성장률에만 집중할 수 있도록 불필요한 부분을 제거한 것이기 때문에 정확한 표현이 아닌 대략의 시간을 표현한다고 생각하면 된다.

예를들어, 위 사진에서 O(n/2)에서 n이 매우 커지면(푸는 문제가 계속 커진다면) O(n)과 점점 비슷해 질 것이다. 결국 1/2는 의미가 없어지기 때문에 O(n/2)도 O(n)이라고 보는 것이다.

주로 사용되는 Big O 표기는 다음과 같다.

• O(n^2)
• O(n log n)
• O(n) ->선형 검색
• O(log n) ->이진 검색
• O(1)

(n에서 시작해 1에 이르기까지 반으로 나누는 횟수를 뜻하는 수학 함수는 2를 밑으로 하는 n의 로그이다.)

Big Ω 표기법
알고리즘 실행 시간의 하한으로, 최상의 경우를 나태는 것이다.(Omega of라고 읽으면 된다.) 예를 들어 선형 검색에서 운이 좋아 맨 앞에 원하는 숫자가 있었다면, 한 번에 검색이 끝나기 때문에 하한은 Ω(1)이 된다.

주로 사용되는 Big Ω(omega of) 표기는 다음과 같다.

• Ω(n^2)
• Ω(n log n)
• Ω(n) - 배열 안에 존재하는 값의 개수 세기
• Ω(log n)
• Ω(1) - 선형 검색, 이진 검색

(항상 운이 좋기를 바랄 수는 없다. "운이 좋으면 이정도밖에 안 걸릴 거야!"보다는 "어떤 상황에서든 이 이상은 걸리지 않을 거야"가 중요하지 않는가. 따라서 보통 Big O표기법을 많이 사용한다.)

선형 검색

전화번호부에서 특정 이름을 찾고 그 사람의 전화번호를 출력하는 프로그램을 작성해보자.

#include <cs50.h>
#include <stdio.h>
#include <string.h>

int main(void)
{
    string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"};
    string numbers[] = {"617–555–0100", "617–555–0101", "617–555–0102", "617–555–0103"};

    for (int i = 0; i < 4; i++)
    {
        if (strcmp(names[i], "EMMA") == 0)
        {
            printf("Found %s\n", numbers[i]);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

문자열을 비교하는 strcmp함수가 사용되었다.

(strcmp함수 두 문자열이 같으면 0을 반환한다. 양수를 반환하면 첫 번째 문자열이 알파벳 기준으로 큰 경우이고, 음수면 그 반대의 경우를 의미한다.)

이 코드의 한계는 names의 배열과 numbers의 배열이 서로 같은 인덱스를 가져야한다는 것이다. 만약 누가 실수로 names의 배열을 다른 방식으로 정렬한다면 EMMA를 검색했을 때 다른 사람의 전화번호(인덱스가 같은)가 나올 수 있다는 것이다.

#include <cs50.h>
#include <stdio.h>
#include <string.h>

typedef struct
{
    string name;
    string number;
}
person;

int main(void)
{
    person people[4];

    people[0].name = "EMMA";
    people[0].number = "617–555–0100";
    people[1].name = "RODRIGO";
    people[1].number = "617–555–0101";
    people[2].name = "BRIAN";
    people[2].number = "617–555–0102";
    people[3].name = "DAVID";
    people[3].number = "617–555–0103";

    // EMMA 검색
    for (int i = 0; i < 4; i++)
    {
        if (strcmp(people[i].name, "EMMA") == 0)
        {
            printf("Found %s\n", people[i].number);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

위 한계를 해결하기 위해 새로운 자료형으로 구조체(struct)를 정의해서 이름과 번호를 묶어주었다. 구조체는 여러 자료형을 담을 수 있는 하나의 그릇같은 존재로, 관련된 정보를 하나로 묶기 위해 사용한다.

typedef struct
{
    string name;
    string number;
}
person;

typedef는 자료형에 이름을 붙일 때 쓰는 키워드다. {} 안에는 어떤 정보가 들어갈 것인지를 적고 괄호 밖에 구조체의 이름을 쓴다.

버블 정렬

버블 정렬은 두 개의 인접한 자료 값을 비교하면서 큰 숫자를 오른쪽으로 교환하는 방식의 정렬 방법이다. 아래는 버블 정렬의 의사코드로 간단하고 직관적이지만 효율성은 떨어진다.

Repeat n–1 times

    For i from 0 to n–2

        If i'th and i+1'th elements out of order

            Swap them

n개의 값이 주어진다면 마지막 값은 그 전 값과 비교되어 정렬되므로 최대 n-1번 비교할 수 있다. 한 바퀴씩 비교를 돌 때마다 배열 안에서 가장 큰 값이 맨 뒤로 가기 때문에 비교 대상은 하나씩 줄어든다.

(n-1) + (n-2) + ... + 1 = n(n-1)/2 이고, 지수가 가장 큰 n^2의 영향력이 가장 크기 때문에 버블 정렬 실행 시간의 상한은 O(n^2)이다.

정렬이 되어 있더라도 컴퓨터는 그저 루프를 돌며 비교할 것이기 때문에 하한도 역시 Ω(n^2)이 된다.

선택 정렬

선택정렬은 배열 안에서 가장 작은 수를 찾아 정렬되지 않은 첫 번째 위치의 수와 교환하는 방식의 정렬 알고리즘이다. 이 역시 직관적인 방법이지만, 교환 횟수는 최소화하는 반면 각 자료를 비교하는 횟수는 증가하게 되어 효율성은 떨어진다.

각각 요소마다 n번, n-1번, n-2번, ... , 1번 비교한다. 이를 계산해보면 N^2/2+n/2가 되는데 이때 역시 n^2의 영향력이 가장 크므로, O(n^2)이 된다. 이미 정렬되어 있더라도 똑같이 실행될 것이기 때문에 하한 역시 n^2로 Ω(n^2)이다.

(선택 정렬이 최소/최대값 중 하나만 찾는 반면 **이중 선택 정렬**은 한 번 탐색할 때 최소값, 최대값을 동시에 찾는다. 먼저 최소, 최대값을 찾아 양끝으로 보낸 후, 다음 루프에서는 양끝 값을 제외하고 나머지에서 최대, 최소값을 찾은 후 각각 또 양끝으로 보내는 과정을 반복한다. 이렇게 동시에 한다면 반복 횟수가 줄어들어 더 효율적이다.)

정렬 알고리즘의 실행시간

지금까지 배운 알고리즘의 실행시간 상한과 하한은 다음과 같다.

• O(n^2): 선택 정렬, 버블 정렬
• O(n log n)
• O(n): 선형 검색
• O(log n): 이진 검색
• O(1)

• Ω(n^2): 선택 정렬, 버블 정렬
• Ω(n log n)
• Ω(n)
• Ω(log n)
• Ω(1): 선형 검색, 이진 검색

그런데 사실 버블 정렬은 실행 시간의 하한을 단축시킬 수 있는 방법이 있다.

만약 정렬이 되어있는 배열이 주어진다면, 바깥쪽 루프를 n-1번 반복하는 것이 아니라 '교환이 일어나지 않을때'까지 수생하도록 바꾸는 것이다. 따라서 버블 정렬의 하한은 Ω(n)이 되어 이 경우 선택정렬보다 더 빠른 방법이 된다.

(선택 정렬은 배열의 한 값에서 나머지 모든 값을 살펴보아야 하기 때문에 시간을 단축시키기는 힘들다.)

재귀

재귀(Recursion) 함수란 함수 내에서 자기 자신을 다시 호출하는 함수이다.

어떤 경우에 함수를 재귀적으로 호출하는지 그 예시로 높이를 입력 받아 #피라미드를 출력하는 코드를 말할 수 있다.

#include <cs50.h>
#include <stdio.h>

void draw(int h);

int main(void)
{
    int height = get_int("Height: ");

    draw(height);
}

void draw(int h)
{
    for (int i = 1; i <= h; i++)
    {
        for (int j = 1; j <= i; j++)
        {
            printf("#");
        }
        printf("\n");
    }
}

높이를 입력 받아 중첩 루프를 통해 피라미드를 출력해주는 draw함수를 정의했다.

여기서 중첩 루프를 사용하였는데 바깥 루프는 안쪽 루프를 반복하는 역할을 한다. 따라서 바깥 루프를 없앤 draw함수를 만들고, 이를 재귀적으로 호출해서 똑같은 작업을 수행할 수 있다.

#include <cs50.h>
#include <stdio.h>

void draw(int h);

int main(void)
{
    int height = get_int("Height: ");

    draw(height);
}

void draw(int h)
{
    if (h == 0)
    {
        return;
    }

    draw(h - 1);

    for (int i = 0; i < h; i++)
    {
        printf("#");
    }
    printf("\n");
}

h라는 높이를 받았을 때, h-1 높이로 draw함수를 먼저 호출하고, 그 후에 h만큼의 #을 출력한다. 내부적으로 호출된 draw 함수를 따라가다보면 h = 0인 상황이 오기 때문에 그 때는 아무것도 출력하지 않는다는 조건문을 추가해야 한다.

    if (h == 0)
    {
        return;
    }

h가 0이라면 멈추라는 말이다. 끝없이 함수가 반복되는 것을 막아준다.

    draw(h - 1);

높이 4의 피라미드를 만들고 싶다면 먼저 높이 3의 피라미드를 그린다.

    for (int i = 0; i < h; i++)
    {
        printf("#");
    }
    printf("\n");

높이 3의 피라미드 밑에 4개의 #을 한 줄 더한다.


재귀함수를 사용하면 복잡한 문제를 간단하게 작성할 수 있으나 호출될 때마다 저장 공간을 차지하므로 적절한 사용이 필요하다.

병합정렬(merge sort)

병합정렬은 재귀를 활용한 정렬 알고리즘으로 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 부분 배열을 정렬하고 다시 합쳐나가는 방식이다.

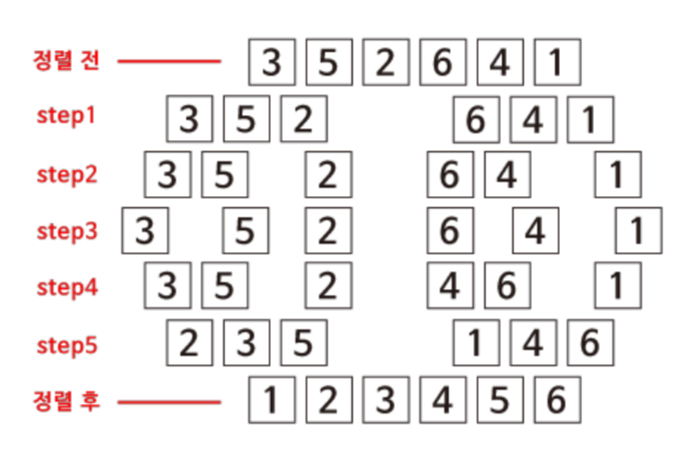
병합 정렬 실행 시간의 상한은 O(n log n)이다. 숫자를 반으로 나누는 데 O(log n)의 시간이 들고, 각 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)의 시각이 걸리기 때문이다.

숫자들이 이미 정렬되었는지 여부에 관계없이 나누고 병합하는 과정이 필요하기 때문에 하한 역시 Ω(n log n)이다. 버블 정렬처럼 더이상 교환이 일어나지 않을 때 멈추는 최적화 기법이 없다.

지금까지 배운 다른 정렬에 비해 효율적이지만 배열을 나누기 때문에 추가적 메모리 할당이 필요하다는 단점이 있다. 또,
이미 정렬되어있는 지 여부에 관계 없이 계속 반복하므로 상황에 따라서 매우 비효율적이다.