이 글은 앞 글과 이어지는 글입니다. 삽입과 조회 및 성능 비교에 관한 내용은 앞 글에 있습니다.

전체 코드는 Github 에서 확인 수 있습니다.

삭제

이전 글에서 삽입, 검색을 구현하였다. 삽입, 검색의 구현도 복잡했지만 삭제는 이들 보다 훨씬 복잡하다. 경우의 수가 많아 복잡하기 때문이다. 때문에 삭제 과정의 경우의 수를 잘 이해하고 코드를 확인하기 바란다.

삽입은 노드에 key를 추가하기에 key 의 개수가 최대 개수를 넘어가면 분리하였다면, 삭제는 노드에 key를 감소하기 때문에 부족한 키의 개수를 채우는 과정이 필요하다. 여러가지 경우에 따라 작업이 달라진다.

삭제 과정

1. 삭제할 key가 leaf 노드에 있고, 삭제후 최소 key 값이 유지되는 경우

1. 노드의 key 값을 단순 삭제한다. key 의 개수가 부족하지 않기에 채울 필요 없다.

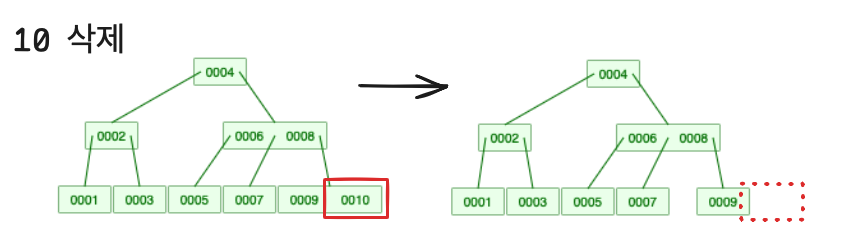
2. 삭제할 key가 leaf 노드에 있고, 삭제후 최소 key 값이 유지되지 않는 경우

• 주변 노드들을 사용해 부족한 key 의 개수를 채운다. 아래 조건을 차순서대로 확인하여 작업을 실행한다.

1. 왼쪽 또는 오른쪽 형제 노드의 key 의 개수가 최소 key 의 개수보다 많은 경우
   1. key 값을 삭제한다.
   2. 부모의 key 값을 가져와 채운다.
   3. 형제 노드의 key 값을 가져와 부모 노드에서 가져온 key 자리로 옮긴다. (왼쪽 형제의 경우 가장 큰 key 값, 오른쪽 형제의 경우 가장 작은 key 값)

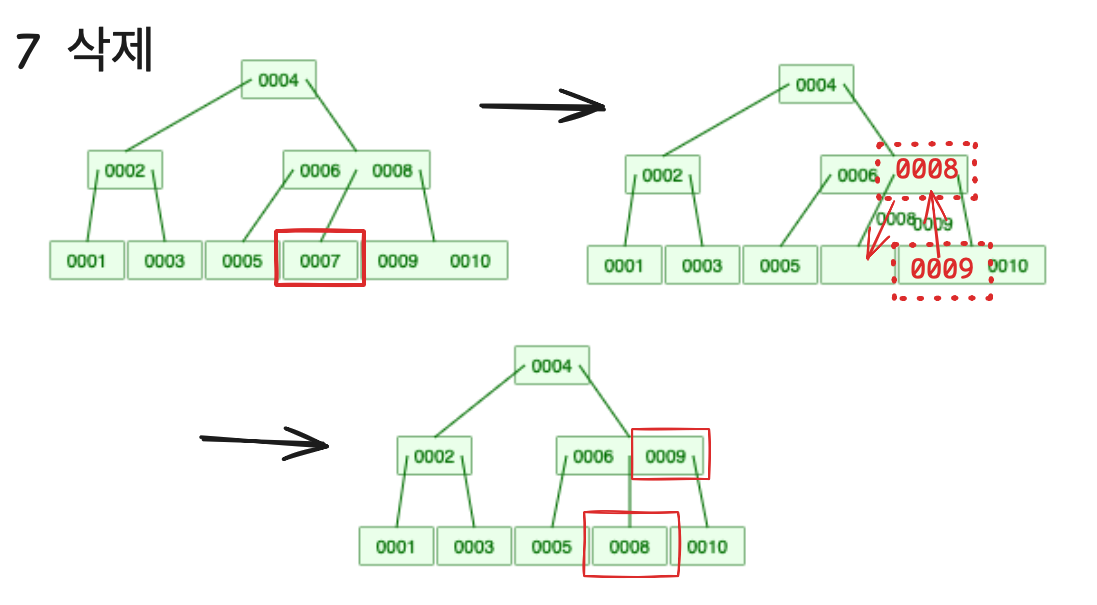
2. 양쪽 형제 노드들의 key 의 개수가 모두 최소 key 의 개수인 경우
   1. key 값을 삭제한다.
   2. 왼쪽 혹은 오른쪽 노드의 key 값들과 부모 노드의 key 값을 합친다.

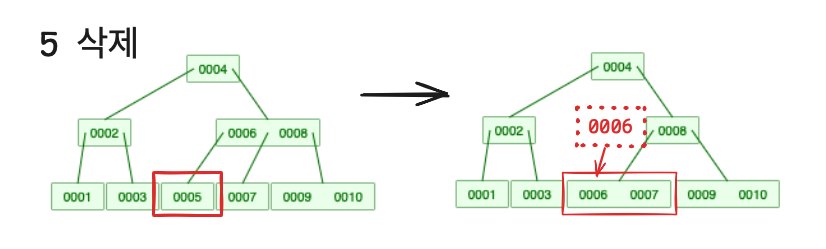
> 이렇게 한후 부모 노드가 최소 key 의 개수를 만족하지 않는 경우 2-1, 2-2 과정을 반복한다.
> 

3. 삭제할 key 가 leaf 노드가 아닌 노드에 있는 경우

1. 선임자나 후임자를 찾는다.
2. 선임자나 후임자와 key 의 위치를 바꾼다.
3. 바꾼 위치의 key 값을 삭제한다.
4. 삭제 후 최소 key 의 개수를 만족하지 않는다면 2-1, 2-2 과정을 반복한다.

선임자 : 나보다 작은 key 값 중 가장 큰 key 값
후임자 : 나보다 큰 key 값중 가장 작은 key 값

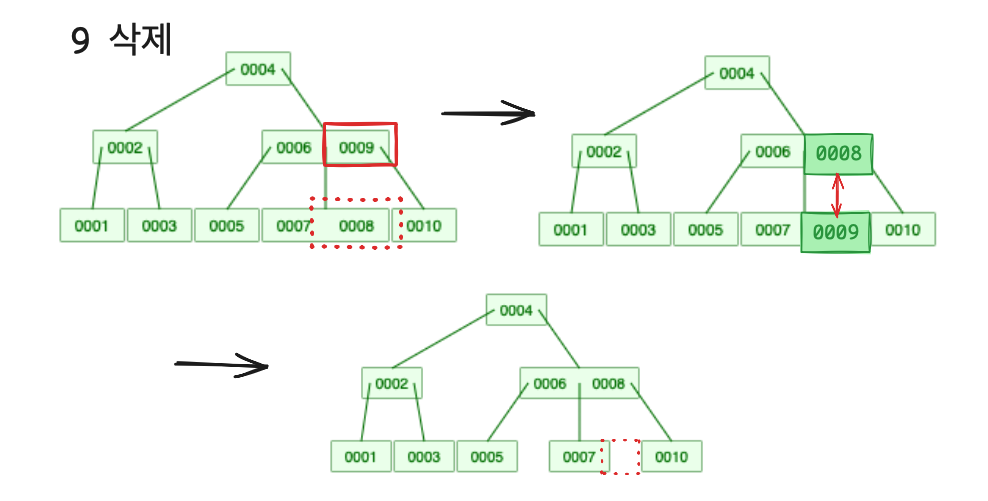
이제 모든 경우의 수를 알아보았으니 코드를 짜보자!

코드

public void delete(int key) {
	delete(root, key);

	// 루트 노드가 키를 잃었을 때, 자식이 있으면 그 자식으로 루트 갱신
	if (root.keys.isEmpty()) {
		if (!root.isLeaf()) {
			root = root.children.get(0);
		}
	}
}

private void delete(BTreeNode node, int key) {
	int idx = node.findKey(key);

	// 1. 키가 현재 노드에 있는 경우
	if (idx != -1) {
		if (node.isLeaf()) {
			// 리프 노드에서 직접 삭제
			node.keys.remove(idx);
		} else {
			// 내부 노드에서 삭제 처리 3.
			deleteInternalNode(node, idx);
		}
	} else {
		// 키가 리프 노드에 없는 경우
		if (node.isLeaf()) {
			return;  // 찾으려는 key 가 없음
		}

		// 키가 없으면 적절한 자식 노드로 이동
		idx = node.getNextNodeIndex(key);
		BTreeNode nextChild = node.children.get(idx);

		//자식 노드에서 삭제
		delete(nextChild, key);
		// 삭제 후 자식 노드의 최소 키 값이 어긋나면
		if (nextChild.keys.size() < minimumKeyCount) {
			// 채워주기
			fill(node, idx);
		}
	}
}

• 삭제도 재귀적으로 삭제 할 key 값을 찾는다.
• key 를 찾은 경우 leaf 노드에서 찾은 경우와 내부 노드에서 찾은 경우로 나뉜다.
  • leaf 노드 라면 key 값을 삭제한다.
  • 내부 노드라면 전임자나 후임자와 위치를 바꾸기 위해 deleteInternalNode() 를 호출한다.
• leaf 노드인데도 key 가 없는 경우 찾으려는 키가 없는 것으로 간주한다.
• 삭제 후 자식 노드의 최소 키 값이 어긋나면 fill() 을 호출해 채워준다.

fill

private void fill(BTreeNode node, int deletedNodeIndex) {
	// 왼쪽 형제에게 빌리는 경우 2-1
	if (deletedNodeIndex != 0 && node.children.get(deletedNodeIndex - 1).keys.size() > minimumKeyCount) {
		borrowFromPrev(node, deletedNodeIndex);
	}
	// 오른쪽 형제에게 빌리는 경우 2-1
	else if (deletedNodeIndex != node.children.size() - 1 && node.children.get(deletedNodeIndex + 1).keys.size() > minimumKeyCount) {
		borrowFromNext(node, deletedNodeIndex);
	}
	else {
		// 왼쪽 형제와 부모노드를 합치는 경우 2-2
		if (deletedNodeIndex != 0) {
			leftMerge(node, deletedNodeIndex);
		}
		// 오른쪽 형제와 부모노드를 합치는 경우 2-2
		else {
			rightMerge(node, deletedNodeIndex);
		}
	}
}

부족한 key 의 개수를 채우는 메서드이다. deletedNodeIndex 는 node 의 자식 중 삭제된 노드의 인덱스를 나타낸다.

• 삭제 된 노드의 형제 노드들을 검사해보고 key 값을 가져올 수 있다면 가져온다. - borrowFromPrev , borrowFromNext
• 가져올 수 없다면 형제와 부모노드를 합치는 작업을 한다. - leftMerge , rightMerge

borrowFrom , merge

private void borrowFromPrev(BTreeNode node, int deletedNodeIndex) {
	BTreeNode deletedChild = node.children.get(deletedNodeIndex);
	BTreeNode sibling = node.children.get(deletedNodeIndex - 1);

	// 부모의 키를 삭제된 자식에 옮김
	deletedChild.addKey(node.keys.get(deletedNodeIndex - 1));
	if (!deletedChild.isLeaf()) {
		deletedChild.children.add(0, sibling.children.remove(sibling.children.size() - 1));
	}
	// 형제 노드의 키를 부모로 옮김
	node.keys.set(deletedNodeIndex - 1, sibling.keys.remove(sibling.keys.size() - 1));
}

private void leftMerge(BTreeNode node, int deletedNodeIndex) {
	BTreeNode deletedChild = node.children.get(deletedNodeIndex);
	BTreeNode sibling = node.children.get(deletedNodeIndex - 1);
	
	// 형제 노드의 키를 삭제된 자식에 옮김
	for (int i = 0; i < sibling.keys.size(); i++) {
		deletedChild.keys.add(i, sibling.keys.get(i));
	}
	if (!deletedChild.isLeaf()) {
		for (int i = 0; i < sibling.children.size(); i++) {
			deletedChild.children.add(i, sibling.children.get(i));
		}
	}
	// 부모 노드의 키를 삭제된 자식에 옮김
	deletedChild.addKey(node.keys.remove(deletedNodeIndex - 1));

	// 합쳐진 형제 노드 삭제
	node.children.remove(sibling);
}

• 형제 노드에서 가져오는 경우 - borrowFromPrev , borrowFromNext → 2-1
  • 삭제된 자식과 가져올 자식을 찾는다.
  • 먼저 부모의 키를 삭제된 자식 노드에 옮긴다.
    • leaf 노드가 아니라면 부모 노드의 key 에 해당하는 자식도 같이 옮긴다.
  • 그 후 가져올 형제 노드로 부터 key 하나를 부모로 옮긴다.
• 형제 노드와 부모의 key 를 합치는 경우 - leftMerge , rightMerge → 2-2
  • 삭제된 자식과 합칠 형제을 찾는다.
  • 합 칠 형제의 key 를 삭제된 자식 노드에 옮긴다.
    • leaf 노드가 아니라면 자식 노드들도 옮긴다.
  • 부모의 키를 옮긴다.
  • 합쳐진 형제 노드를 삭제한다.

deleteInternalNode

private void deleteInternalNode(BTreeNode node, int deletedKeyIndex) {
	BTreeNode nextChild;
	// 선임자와 바꾸는 경우
	if (node.children.get(deletedKeyIndex).keys.size() >= minimumKeyCount) {
		int pred = getPredecessor(node, deletedKeyIndex);
		node.keys.set(deletedKeyIndex, pred);
		nextChild = node.children.get(deletedKeyIndex);
		delete(nextChild, pred);
	} 
	// 후임자와 바꾸는 경우 
	else {
		int succ = getSuccessor(node, deletedKeyIndex);
		node.keys.set(deletedKeyIndex, succ);
		nextChild = node.children.get(deletedKeyIndex + 1);
		delete(nextChild, succ);
	}
	// 선임자 혹은 후임자와 바꾸고 삭제 한 후 최소 key 개수를 만족하지 않는다면
	if (nextChild.keys.size() < minimumKeyCount) {
		// 부족한 값을 채운다.
		fill(node, deletedKeyIndex);
	}
}

// 선임자 혹은 후임자의 key 값을 반환
private int getPredecessor(BTreeNode node, int idx) {
	BTreeNode current = node.children.get(idx);
	while (!current.isLeaf()) {
		current = current.children.get(current.keys.size());
	}
	return current.keys.get(current.keys.size() - 1);
}

삭제 조건 3. 에 해당하는 경우를 처리하는 메서드이다.

• 선임자와 바꿀지 후임자와 바꿀지 찾는다. (삭제할 자식의 키의 개수를 기반으로 찾는다.)
• 선임자 혹은 후임자 key 값을 찾는다.
• 삭제할 노드의 아래 노드중 선임자 혹은 후임자의 key 값을 삭제한다.
• 최소 개수를 만족하지 않는다면 채운다.

borrowFromPrev , borrowFromNext , leftMerge , rightMerge, getPredecessor , getSuccessor 들은 두가지 경우 모두 비슷한 코드라서 하나의 코드만 설명했다.

이렇게 삭제 코드 까지 알아보았다.