알고리즘(reet_code)정리
1.트리 순회 (전위, 후위, 중위)
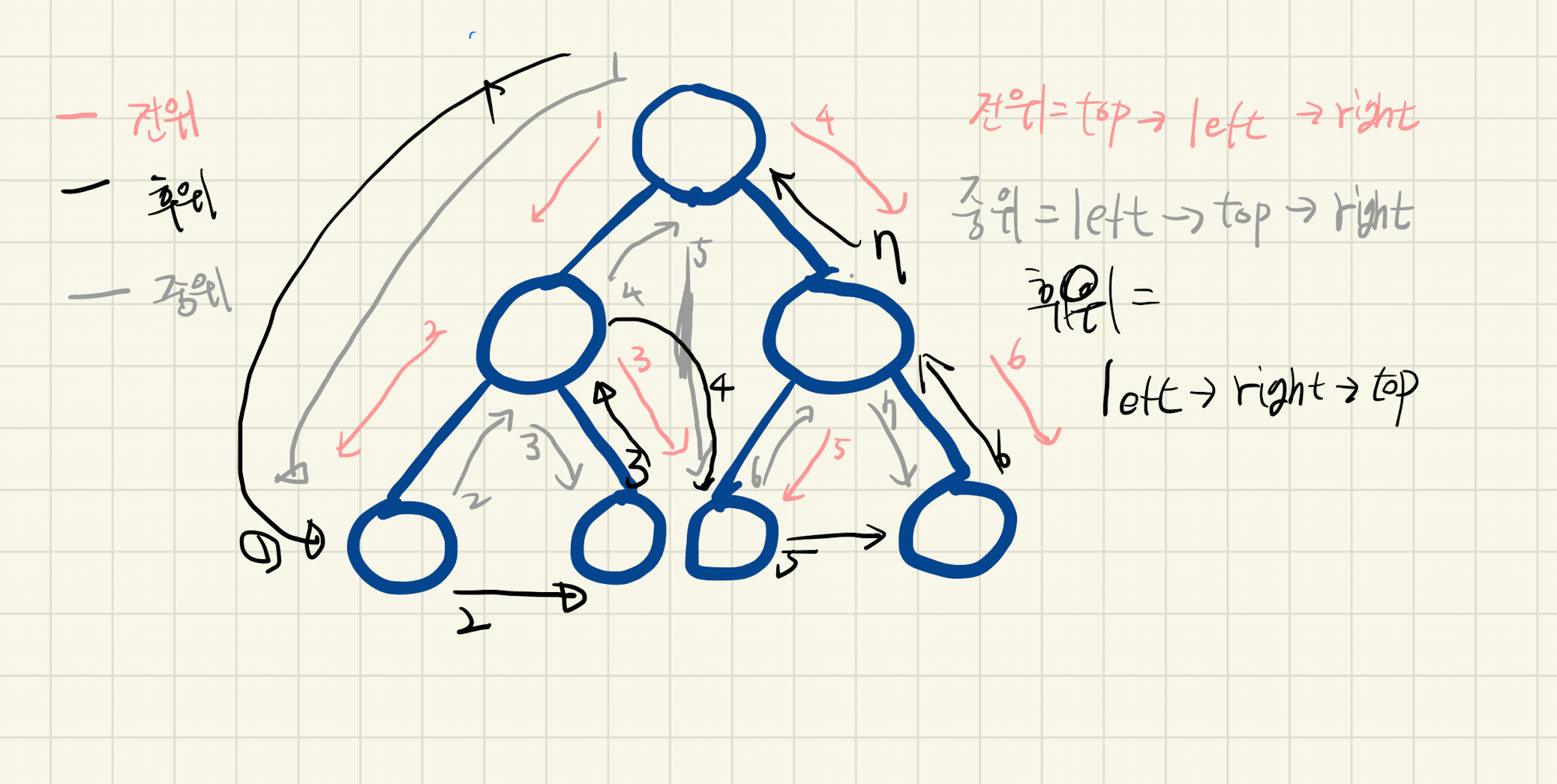
전위:전위 순회는 우선순위가 적혀 져있는대로 top -> left -> right 이다. 매 노드에서 left를 먼저간 후 right를 간다.스택을 이용한 반복문으로 쉽게 구현할 수 있다. 시간 복잡도는 O(N).후위:후위 순회는 우선순위가 left -> right -
2.이진탐색트리 (BST)
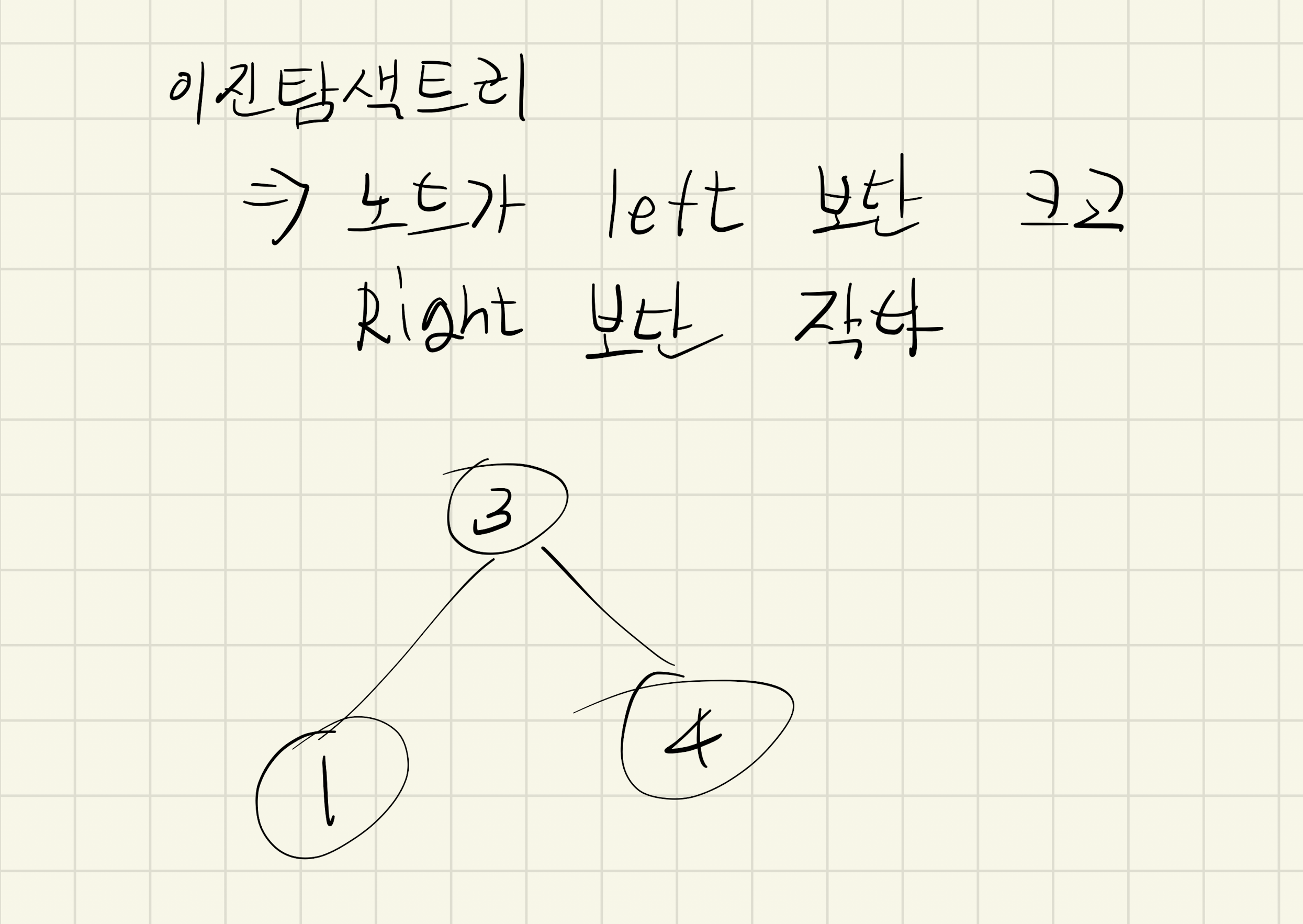
이와 같이 부모노드가 왼쪽 자신노드보다 크가 오른쪽 자식 노드보다 작은 이진 트리를 이진 탐색 트리라고 한다.val 와 root 노드를 입력받아 자식 노드중 val와 값이 일치하는 노드가 있다면 그 노드를 root로 삼는 서브 트리를 반환하는 문제이다.현재 탐색중인 노
3.Sliding Window
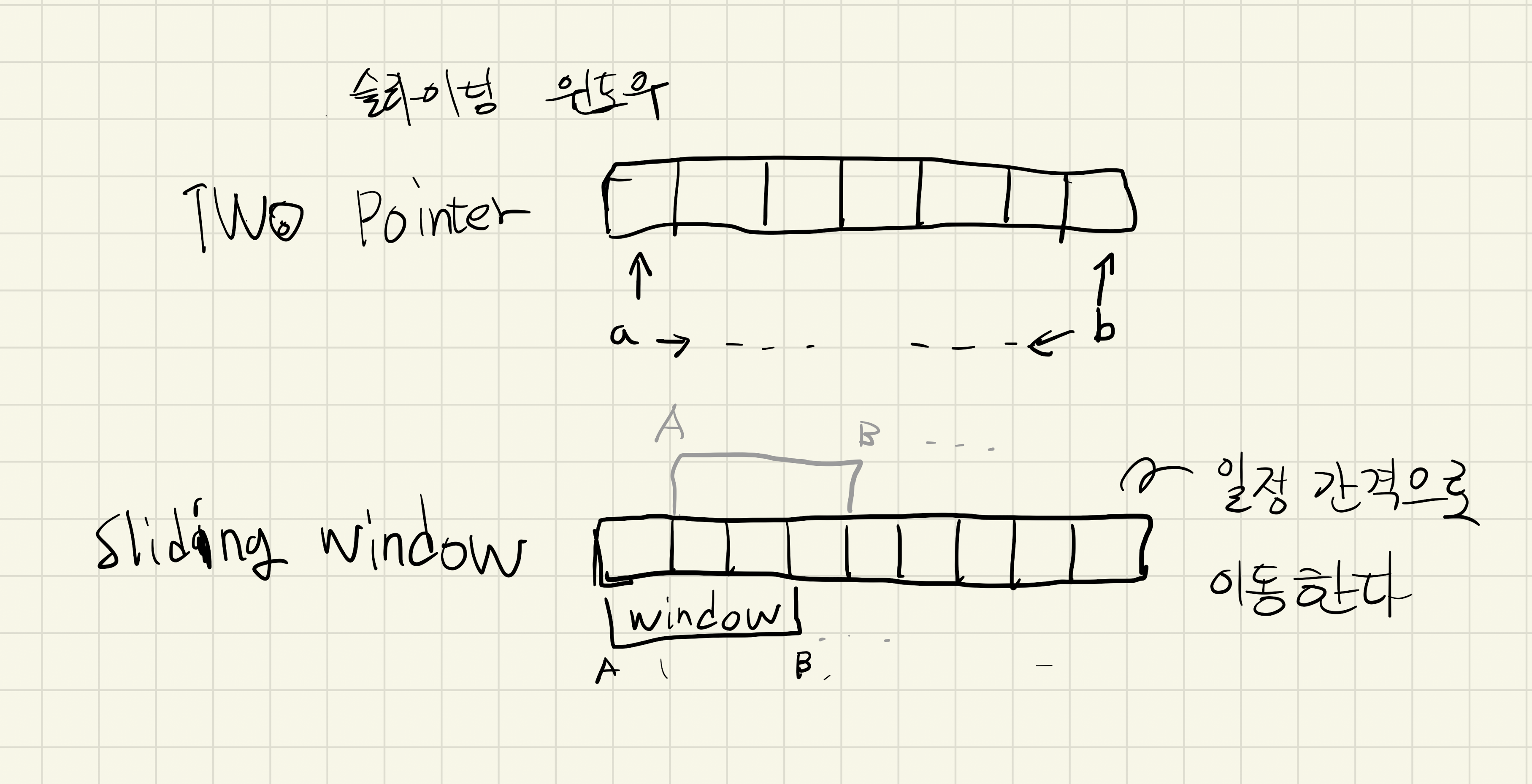
투포인터 알고리즘과 비슷하지만 일정 간격을 두고 두 포인터가 끝을향해 나아간다는 점에서 다르다윈도우 슬라이딩 이라는 알고리즘을 처음 접해본 문제이다.....접근법과 해결책은 비슷하게 생각해 냈는데 그걸 구현하는데 문제가 많아 결국 솔루션을 보고 말았다.가만 보니 기본적
4.BFS 와 동적 프로그래밍

너비우선 탐색과 동적프로그래밍을 적용시켜 문제를 해결했다. 중급 문제이므로 너비우선탐색과 동적 프로그래밍을 안다 생각하고 설명하겠습니다.확실히 푸는것보다 말로, 글로 설명하는게 훨씬 어려운것 같다. 풀고나서 되돌아보면 아주 기본적인 문제인것 같은데 막상 풀때는 정말 힘
5.77.Combinations(재귀호출)

재귀호출을 통해 해결했다.중급 문제였는데 왜 중급 문제인지는 모르겠다. 좀 쉬운 편이 아닌가 생각된다. 백준은 문제 등급이 섬세하게 나뉘어 있어 좋은데 reet코드는 같은 중급 문제여도 난이도가 천차만별인 것 같다. 그래도 reet코드는 solution을 찾기가 쉽고
6.2. Add Two Numbers

처음 문제를 풀려했을때는 리스트에 값을 저장한뒤 reverse()메소드를 통해 뒤집고 join('')하여 parseInt()를 통해 정수로 만들고 더한 뒤 다시 이를 배열로 만들어 링크드 리스트에 저장하는 방식으로 접근했다.하지만 수의 크기가 너무 커졌을때 문제가 해결
7.5. Longest Palindromic Substring

거꾸로 해도 똑같은 즉 회문의 서브 스트링을 찾는 문제이다.중간 난이도였으며, 투포인터를 통해 접근했다.쉬웠던 문제라고 생각한다. 문자열의 i인덱스부터 시작해서 i이후에 같은 문자가 등장하는지 확인한 후 이 i부터j까지의 부분문자열이 회문인지 확인한다. 이후 회문이라면
8.11. Container With Most Water

해결법이 생각이 나지 않아 솔루션을 보고서야 이해했다.투포인터 접근이다.water container의 너비는 가로 \* 세로의 사각형이다.i = 0, j = height - 1로 두게되고 투포인터를 서서히 좁힐때, 사각형의 너비가 첫 경우보다 커지는 경우는 가로길이는
9.1655 가운데를 말해요 <백준>
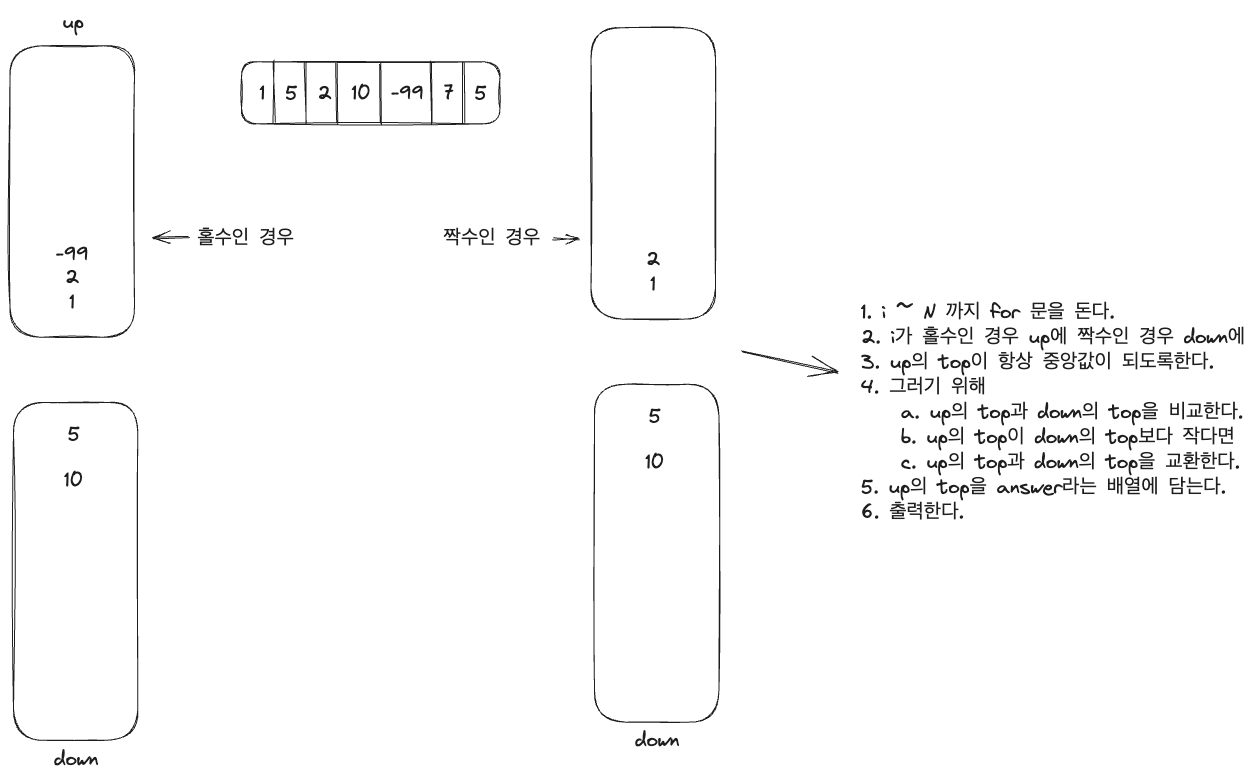
백준이는 동생에게 "가운데를 말해요" 게임을 가르쳐주고 있다. 백준이가 정수를 하나씩 외칠때마다 동생은 지금까지 백준이가 말한 수 중에서 중간값을 말해야 한다. 만약, 그동안 백준이가 외친 수의 개수가 짝수개라면 중간에 있는 두 수 중에서 작은 수를 말해야 한다.예를
10.백준 6549 히스토그램에서 가장 큰 직 사각형
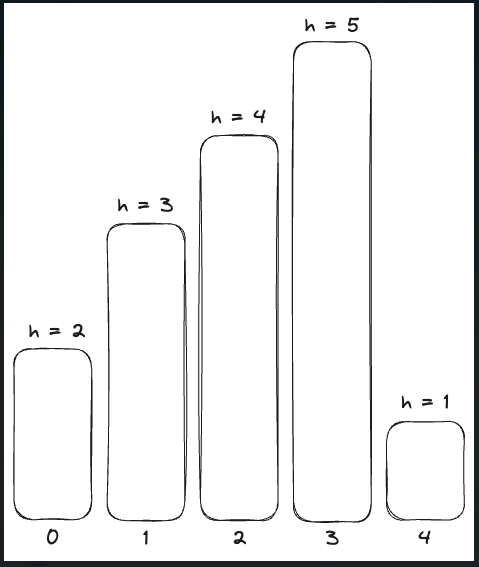
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.히스토그
11.동적 프로그래밍 (프로그래머스 정수 삼각형)

동적 프로그래밍(Dynamic Programming, DP)은 복잡한 문제를 여러 개의 간단한 하위 문제로 나누어 풀고, 그 결과를 저장하여 중복 계산을 피하는 방법을 말합니다.동적 프로그래밍에서 하위 문제를 통해 해결해 나가는 방식은 다음 두 가지의 방식이 있습니다.