문제
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.

히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
정답
#include <iostream>
#include <stack>
using namespace std;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
while (true) {
int N;
cin >> N;
if (N == 0) {
break;
}
stack<pair<int, int>> stk;
long long maxValue = 0;
for (int i = 0; i < N; i++) {
int value;
cin >> value;
int idx = i;
while (!stk.empty() && stk.top().second >= value) {
maxValue = max(1LL * (i - stk.top().first) * stk.top().second, maxValue);
idx = stk.top().first;
stk.pop();
}
stk.push(make_pair(idx, value));
}
while (!stk.empty()) {
maxValue = max(1LL * (N - stk.top().first) * stk.top().second, maxValue);
stk.pop();
}
cout << maxValue << "\n";
}
}해설
우선 이 문제는 스택으로 해결 할 수 있다.
중요한것은 스택에 삽입되는 모든 n번 째 히스토그램은 이후에 만나는 자신보다 낮은 높이의 히스토그램인 i번 째 히스토그램까지 자신의 높이를 h로 가지는 직사각형인 i - n x h를 그릴 수 있다는 점이다. 이때 i - n은 그렇게 되면 이 사각형의 높이로 만들어 낼 수 있는 최대 너비의 사각형이 된다. 다음을 살펴보자.
다음과 같은 히스토그램이 있다.
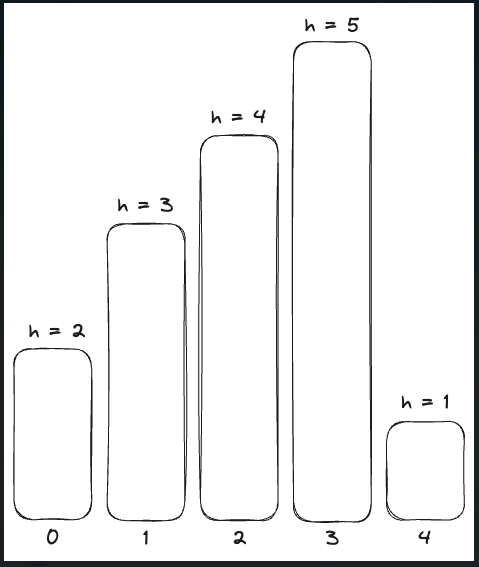
이 히스토그램에서 0번 째 직 사각형은 자신보다 높이가 낮은 인덱스인 4까지 자신의 높이를 h로 가지는 직 사각형을 가질 수 있다. 다음과 같이
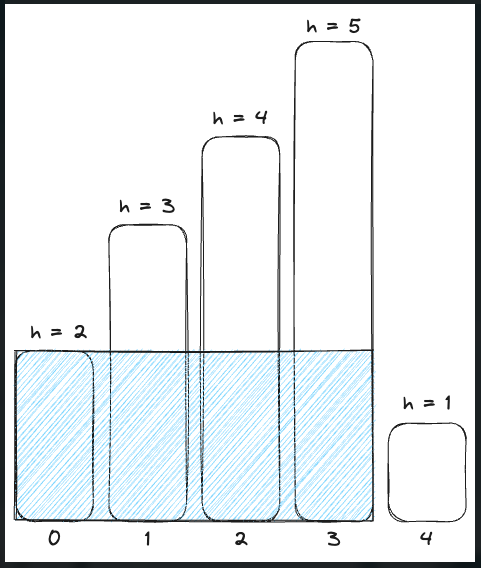
1번 째 사각형 또한 마찬 가지다.
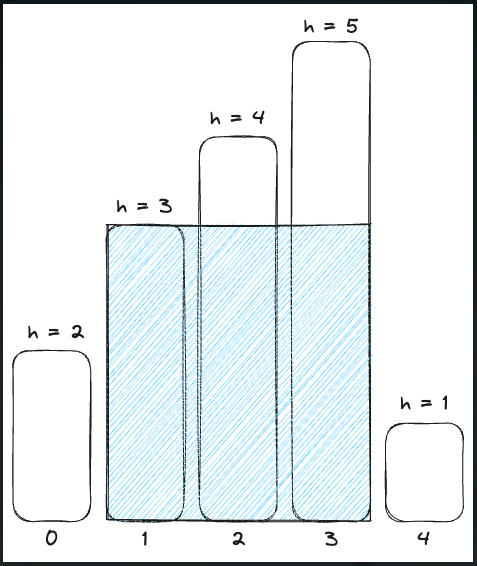
즉 사각형이 오름차순으로 입력될 때 각 사각형은 자신의 높이인 h와 w(히스토그램의 현재 너비) - i(각 사각형의 인덱스)를 가지는 직 사각형을 만들 수 있다.
그렇다면 이걸 스택에 담아보자.
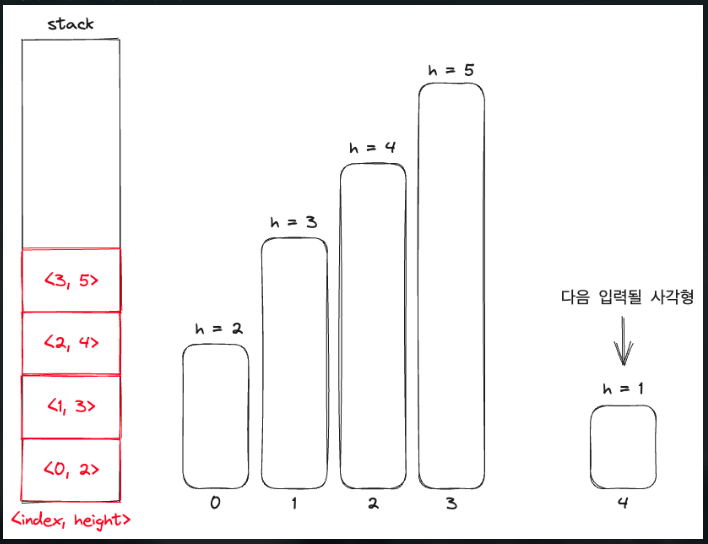
계속해서 큰 값이 들어오지 않는다. 작은 값이 들어왔을 때 어떻게 대응할지 알아보자. 계속 말했다시피 각 사각형은 자신의 높이보다 작은 사각형 a의 전까지의 너비를 너비로 가지는 즉, ia - i * h를 너비 높이로 가지는 직 사각형을 만들어낼 수 있다.
자신의 높이보다 작은 높이의 사각형을 만나면 더 이상 자신의 높이를 높이로 가지는 사각형을 넓혀갈 수 없다. 스택에 담겨 있는 사각형들은 오름차순으로 담겨야 의미가 있다.
그렇다면 다음 입력될 사각형이 들어온다면 어떻게 해야할까?
다음을 보자
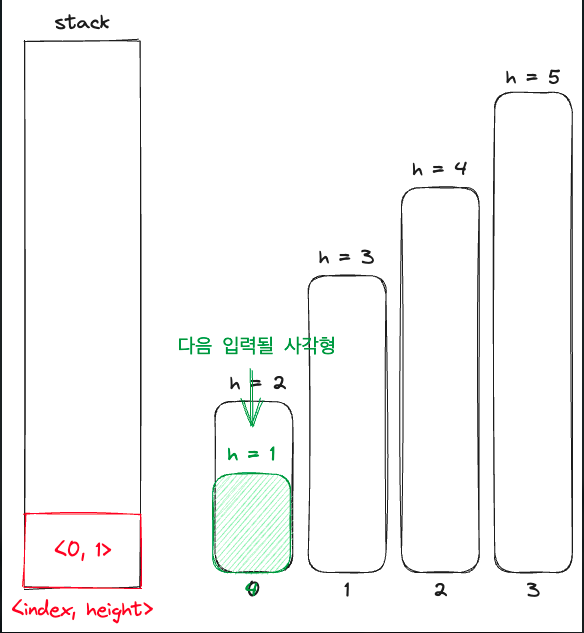
이런식으로 입력될 사각형의 높이보다 높은 사각형들을 모두 스택에서 비워준다. 이후 위 그림처럼 입력될 사각형보다 높이가 낮은 사각형의 바로 앞 위치에 입력될 사각형을 두고 마치 자리를 바꾼것 처럼 동작하도록 한다.
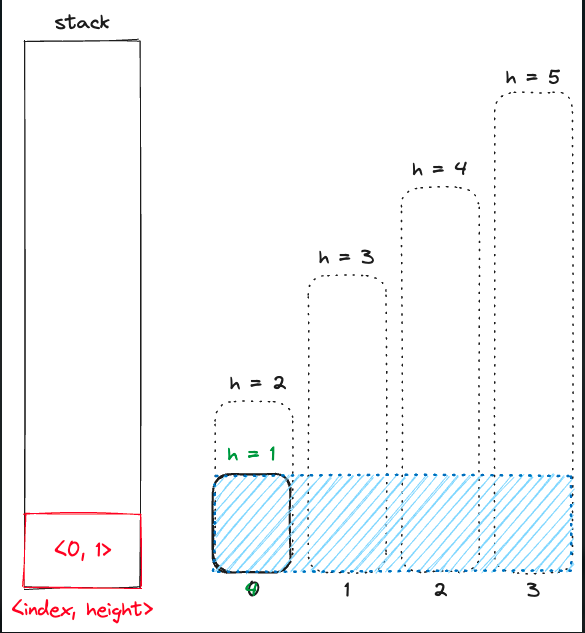
위 그림처럼 다시 스택의 사각형들을 갱신하는 것이다. 이 스택을 비우는 과정에서 비워지는 사각형들의 높이로 만들 수 있는 직 사각형의 너비를 구한다. 아래 그림처럼.
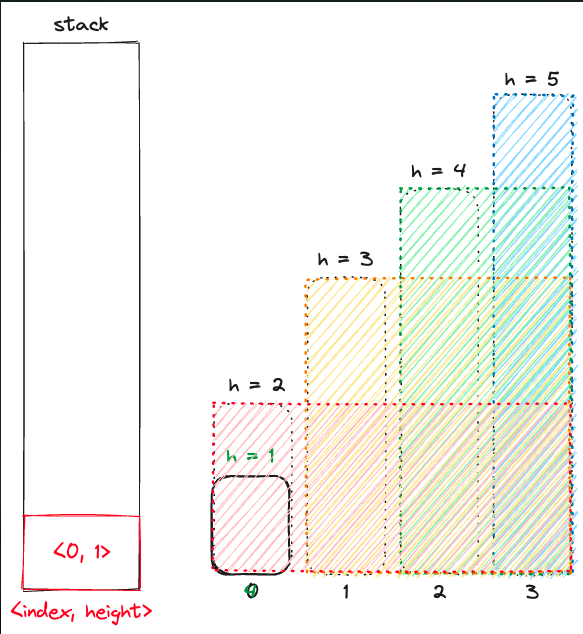
이후는 다시 사각형들을 갱신해간다.
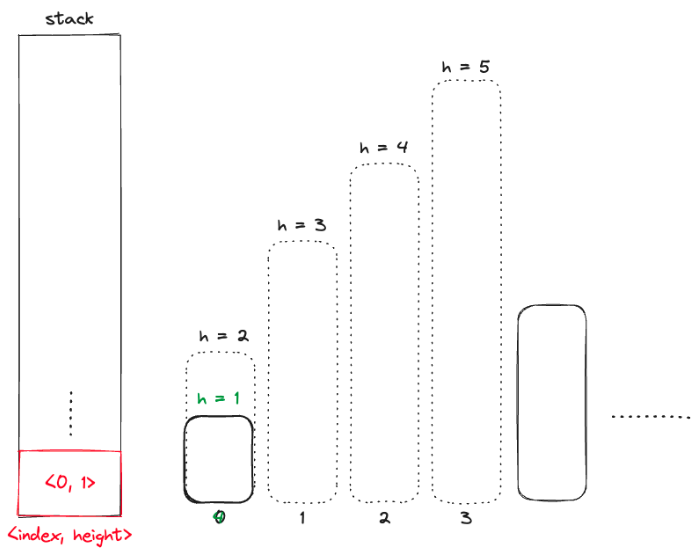
진행하다 스택의 가장 위 사각형보다 작은 사각형이 등장하면 스택을 정리해주는 과정을 거치며 너비를 구해준다. 마지막에는 만약 스택이 비지 않았다면 거기서 사각형들의 너비를 구해주면 된다.
