Optimizer

Optimizer란?

• 딥러닝에서 Network가 빠르고 정확하게 학습하는 것을 목표로 해서 Gradient Descent algorithm을 기반으로한 SGD에서 변형된 여러 종류의 Optimizer가 사용된다.

SGD

• $w_{t+1} = w_t - \eta \nabla_w J(w_t)$

Momentum

• SGD의 경우 기울기가 이전과 동일하다면 step의 길이도 동일하게 update된다. 또한, 기울기 = 0인 지점에서 update가 되지 않기 때문에 local minima에 수렴할 수 있다..
  
• 이러한 문제를 해결하고자 SGD에 관성의 개념을 적용시킨 방법이다.
  $V_t = m \times V_{t-1} - \eta \nabla_wJ(w_t)$
  $w_{t+1} = w_t + V_t$
  • 이전 이동거리와 관성계수(m)에 따라 parameter를 update하도록 하였다. (일반적으로 m = 0.9)
    
  • 관성 개념에 의해 최적 parameter에 더욱 빠르게 학습할 수 있으며, gradient 값이 0인 곳에서도 관성에 의해 local minima를 빠져나갈 수 있다.

Nesterov Accelerated Gradient(NAG)

• Momentum은 update 과정에서 기울기 값을 기반으로 미래값을 도출하도록 되어있으므로, 최적의 parameter를 관성에 의해 지나치게 되는 문제가 생길 수 있다.

• 그래서 NAG는 이동된 지점의 기울기를 활용하여 update를 하는 방법으로 이러한 문제를 해결한다.

  

  $V_t = m \times V_{t-1} - \eta \nabla_wJ(w_t - m \times V_{t-1})$
  $w_{t+1} = w_t + V_t$

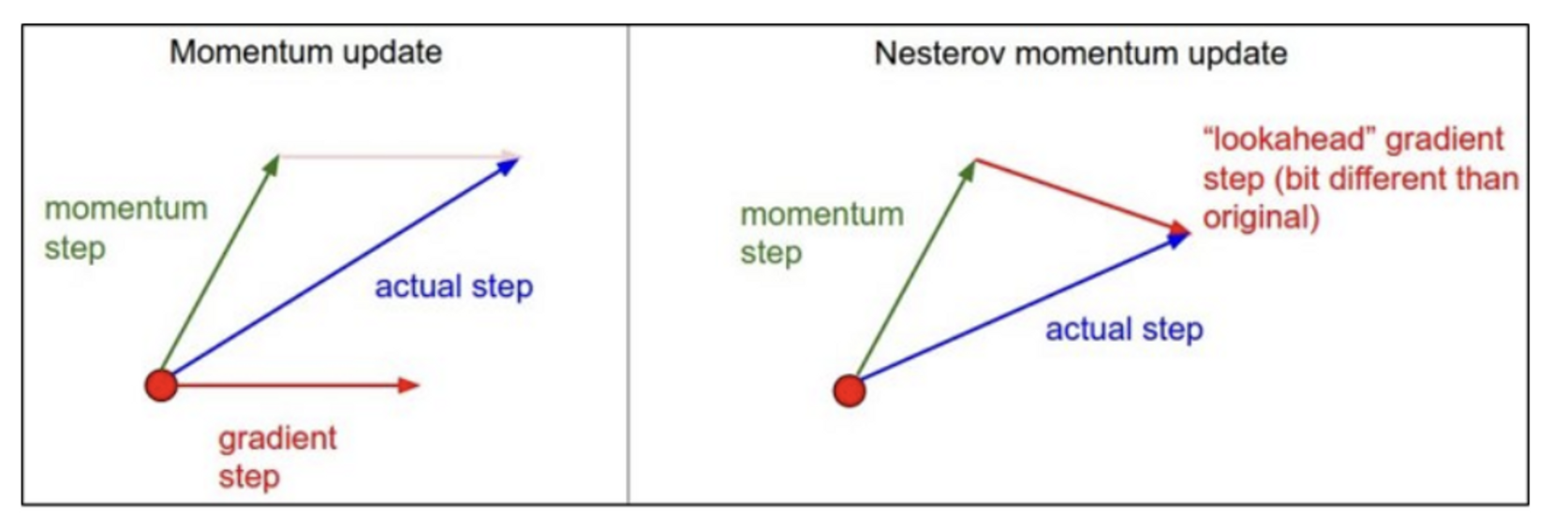
  ⇒ 이동된 곳의 기울기를 적용하므로, 최적의 parameter에서 멈출 수 있다.
  

Adaptive Gradient(Adagrad)

• 동일 기준으로 update되던 각각의 parameter에 개별 기준을 적용하였다. ⇒ 지속적으로 변화하던 parameter보다 한 번도 변하지 않는 parameter에 더 큰 변화를 줘야한다는 개념이다.
  $G_t = G_{t-1} + (\nabla_wJ(w_t))^2 = \sum^k_{i=1}\nabla_{w_i}J(w_i)$
  $w_{t+1} = w_t - {\eta \over \sqrt{G_t + \epsilon}}* \nabla_w J(w_t)$
  ⇒ 학습이 진행됨에 따라 변화 폭이 줄어들어 결국 update되지 않는다.
  

RMSProp

• Adagrad의 문제점을 개선하기 위해 $G_t$ 계산식에 지수이동평균을 적용하였다. ⇒ 학습의 최소 step은 유지
  $G_t = \gamma G_{t-1} + (1 - \gamma)(\nabla_wJ(w_t))^2$
  $w_{t+1} = w_t - {\eta \over \sqrt{G_t + \epsilon}}* \nabla_w J(w_t)$

Adam

• RMSProp + Momentum
  $m_t = \beta_1m_{t-1} + (1-\beta_1)\nabla_w J(w_t)$

Reference

[1] https://onevision.tistory.com/entry/Optimizer-의-종류와-특성-Momentum-RMSProp-Adam