1. 행렬(Matrix)

우리가 다루고자 하는 센서인 카메라, 라이다 등은 센서 주변의 환경에 대한 정보를 수집할 수 있다. 다만, 이때 취득되는 센서값은 하나의 수로 표현되지 않고, 더욱 다양한 정보를 포함하기 위하여 몇 개의 수를 묶어서 표현된다. 예를 들어, 카메라 센서의 경우 주변 환경에 대한 색상 정보를 표현하기 위해 RGB값(0~255, 0~255, 0~255)으로 센서값이 구성되어 있으며, 라이다 센서값의 경우 (x, y, z, intensity) 등으로 구성된다.

이러한 형태의 센서값에서 쓸만한 정보를 추출하기 위하여 우리들은 여러가지 연산을 센서값에 적용하게 될 텐데, 이를 위해 $x = 7R+8G+9B$(카메라 센서의 경우)와 같은 식으로 표현하는 것은 매우 비효율적이며, 해당 연산의 특성을 파악하기에도 불편하다. 앞의 예시는 비교적 간단하지만, 3차원의 RGB 데이터에서 추출해내야할 정보의 차원은 매우 클 수도 있으며, 특히 deep neural network를 사용할 경우 network 내부에서 데이터의 차원이 수백, 수천으로 늘어나는 일은 매우 흔하다. 따라서 다변수 데이터를 처리함에 있어 발생하는 표현의 문제를 해결하기 위해 행렬(matrix)를 도입하여 다변수 데이터에 대한 연산을 표현한다.

이때 $\bm{A}$처럼 row(행, 가로, $A_{11},A_{12},A_{13}$은 같은 row), column(열, 세로, $A_{11},A_{21},A_{31}$은 같은 column)에 걸쳐 여러개의 수를 포함하고 있는 것을 행렬이라고 하며, $\mathbf{x}$와 같이 column 하나로(혹은 row 하나로)이루어진 것을 벡터(vector)로 구분한다. 위의 예시는 벡터 $\mathbf{x}$가 행렬 $\bm{A}$에 의해 $\mathbf{x'}$로 변환된 것으로 이해할 수 있다. 따라서 행렬이 가지고 있는 특성을 학습하면, 행렬에 의해 주어지는 변환에 대한 분석이 가능하다.

또한 행렬을 여러 벡터의 조합으로 생각할 수도 있는데, 같은 row에 있는 원소들($A_{11},A_{12},A_{13}$ 등)을 하나의 벡터로 보고 row vector들의 조합으로 볼 수도 있으며, 같은 column에 있는 원소들($A_{11},A_{21},A_{31}$ 등)을 하나의 벡터로 보고 column vector들의 조합을 볼 수도 있다.

이러한 표현 방식은 행렬-벡터 간 곱에서 다양한 관점을 제공할 수 있으며, 앞으로의 글에서 다양하게 활용될 것이다.

2. 선형 변환(Linear transform)

어떠한 데이터를 변환하는 방법은 매우 여러가지가 있다. 예를 들어 $x \rightarrow 1, y \rightarrow 2$와 같은 규칙을 정하는 것도 하나의 변환이라고 할 수 있다. 하지만 SLAM(Simultaneous Localization and Mapping)을 학습함에 있어 주목해야하는 변환은 선형 변환(linear transform)이며, 선형 변환은 다음의 조건을 만족하는 변환이다.

이때, $x, y$는 벡터, $L$은 변환 함수, $\alpha$는 상수 값(스칼라 값)이다. 이러한 선형변환은 아래와 같이 행렬을 통해 표현될 수 있다.

SLAM이란 로봇 주변 환경에 대한 지도를 작성함과 동시에 로봇의 위치 및 자세를 동시에 추정하는 문제이다. 이 문제에서 로봇은 주어진 환경에서 지속적으로 이동하며, 이에 따라 로봇에 부착된 센서 또한 함께 움직인다. 우리는 계속 위치가 변화하는 센서로부터 수집된 데이터를 분석하여 하나의 지도를 그려야하며(센서 데이터에 대한 변환), 센서(로봇)의 위치 및 자세를 지도가 그려지는 좌표계에서 표현할 수 있어야 한다(로봇 위치 및 자세에 대한 변환). 여기서 행렬(선형변환)이 사용되는데, 회전과 같이 일반적으로 생각할 수 있는 로봇의 움직임을 행렬(선형변환)을 통해 나타낼 수 있기 때문이다.

만약 행렬로 나타낸 변환을 여러 개 적용하고 싶다면 $\mathbf{x'}=\bm{B}\bm{A}\mathbf{x}$와 같이 행렬을 곱하여 나타낼 수 있다. 행렬의 곱에서는 교환법칙이 성립되지 않는 것 또한 두 변환을 적용하는 순서가 달라지면 결과가 달라지는 것으로 생각하면 자연스럽다.

2-1. 선형 변환의 예시: 회전변환

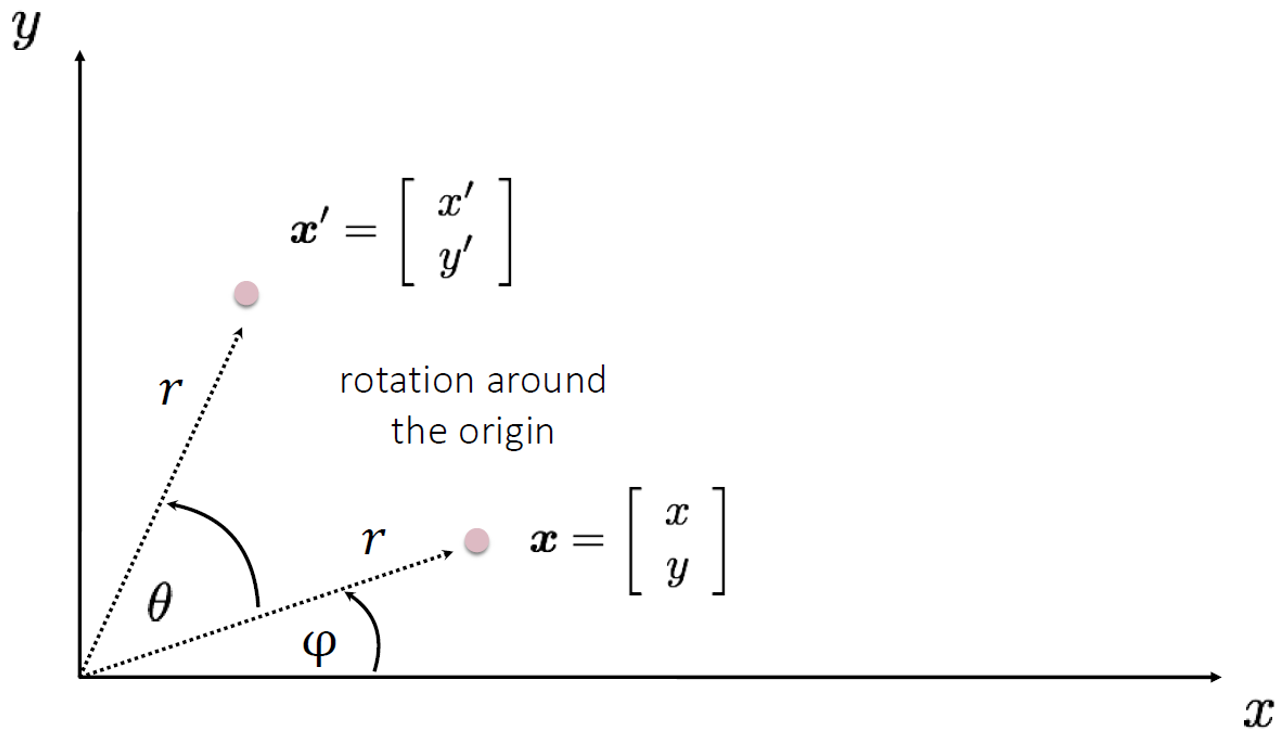
Figure 1. 점의 회전변환

위 그림에서 각 점의 좌표는 다음과 같이 나타낼 수 있다.

• $x=r\cos\Phi, y=r\sin\Phi$
• $x'=r\cos(\Phi+\theta), y'=r\sin(\Phi+\theta)$

두번째 식에서 삼각함수 공식을 적용하면 다음과 같다.

• $x'=r\cos\Phi\cos\theta-r\sin\Phi\sin\theta$
• $y'=r\cos\Phi\sin\theta+r\sin\Phi\cos\theta$

이 두식을 정리하면 다음과 같다.

• $x'=x\cos\theta-y\sin\theta$
• $y'=x\sin\theta+y\cos\theta$

또한 위의 결과는 다음과 같이 행렬로 표현할 수 있다.

즉 원래의 좌표에 회전 변환을 나타내는 행렬을 곱하여 회전된 위치의 좌표를 얻을 수 있고, 다른 변환 역시 각 변환에 해당하는 행렬을 원래의 좌표에 곱하여 변환된 위치의 좌표를 얻을 수 있다.

2-2. 좌표계 변환

위의 예시는 카메라 영상이나 LiDAR의 point cloud 데이터를 변환하기 위해 응용될 수 있다. 그렇다면 로봇의 포즈를 변환하기 위해서는 어떻게 해야할까? 방법 자체는 거의 비슷하나 관점의 차이가 있다. 좌표계 변환을 살펴보기 전에 좌표계가 무엇인지 이해해보자.

2-2-1. Vector Space

일반적으로 좌표라는 말을 들으면 x-y좌표계와 같은 형태를 떠올릴 것이다. 이러한 x-y좌표계는 x값과 y값을 사용하여 공간 상의 어떤 위치를 표현하게 된다. 먼저, 여기서 공간이란 space이며 수학에서 space는 여러 종류가 있지만, 이 글에서 우리는 이미지 픽셀이나 LiDAR 포인트 등 여러가지 벡터 형태의 데이터를 다루게 될 것이므로 vector space에 주목해야 한다.

어떤 집합 V가 다음과 같은 벡터합(vector summation)과 스칼라곱(scalar multiplication)에 대해 닫혀있을 때, 집합 V를 linear space 또는 vector space (over the field R)이라고 한다.

이를 통해 0과 음의 원소의 존재(+연산을 이용) 및 $\alpha(\beta u) = (\alpha\beta)u$ 와 같은 결합법칙(scalar multiplication을 이용) 등을 유추할 수 있으며, $(\alpha + \beta)v = \alpha v + \beta v, \alpha(v + u) = \alpha v + \alpha u$ 와 같은 분배법칙 또한 두 연산의 조합으로 유추할 수 있다.

이러한 vector space V의 subset인 S가 V와 마찬가지로 vector summation과 scalar multiplication에 대해 닫혀있으며 0을 포함하고 있을때 S를 subspace라고 한다.

2-2-2. Basis

위에서 vector space는 벡터합과 스칼라곱에 닫혀있음을 보았고, 이는 vector space에 속해있는 어떤 vector는 다른 vector들의 벡터합과 스칼라곱으로 표현될 수 있음을 의미한다.

이러한 벡터합과 스칼라 곱을 선형 결합(linear combination) 이라고 하는데 다음과 같이 정리할 수 있다.

여기서 $v_i$는 vector space $V$에 속해있는 임의의 벡터이며, $\alpha_i$는 각각에 대응하는 스칼라 값이다. 즉, 위 식의 오른쪽 항에서 vector space $V$의 $v_i$들을 선형 결합하여 새로운 subspace $S$를 생성하고 있으며, $S \sube V$이다. 또한 이와 같이 어떤 벡터들 $v_i$의 선형 결합을 이용하여 어떤 space $S$의 원소들을 모두 표현할 수 있을 경우, $v_i$들이 space $S$를 span한다고 한다.

어떤 space $S$를 span하는 벡터들의 종류는 무수히 많을 수 있다. 예를 들어 좌표 (2, 2)를 표현하는 식은 $2 \cdot (0,1)+2 \cdot (1,0)$, $1 \cdot (2,1) + 1 \cdot (0,1)$ 등 여러가지가 될 수 있다. 하지만 space $S$를 span하는 벡터들 중 다음을 만족하는 특이한 벡터들이 있다.

즉, $v_i$들의 선형결합이 0이 되는 경우가 모든 상수항 $\alpha_i$가 0이 되어야 하는 경우 밖에 없을 때 $v_i$들을 서로 선형 독립(linear independent) 이라고 한다. 또한 $v_i$ 중 하나의 벡터를 다른 벡터들의 선형 결합으로 나타낼 수 없을 때 $v_i$들을 선형 독립이라고 하기도 하며, 위 식을 만족할 경우 이러한 성질을 갖는다. 만약 위에서 $\alpha_i$ 중 하나($\alpha_l$)가 0이 아니라고 가정하면, $v_l = \frac{1}{\alpha_l}\sum_{i=1}^{k}{\alpha_i v_i}$와 같이 $v_l$을 다른 벡터들의 선형 결합으로 나타낼 수 있게되어 선형 독립이 아니게 된다.

어떤 space $S$에서 basis란 space $S$를 span하는 벡터들의 조합 중 서로 선형 독립인 벡터들을 의미한다. 이러한 basis들이 중요한 이유는 일반적으로 어떤 좌표계의 축을 basis를 이용하여 나타내기 때문이다. 예를 들어, 가장 일반적인 x-y좌표의 경우 2가지 축이 있으며, 이는 x축((1,0))과 y축((0,1))이다. 이 둘은 서로 선형 독립이며(x축의 선형 결합으로 y을 나타낼 수 없다), x-y좌표 내의 모든 위치를 span할 수 있다. 일반적으로 x-y좌표에서 사용되는 벡터 $(a, b)$는 해당 백터가 $a \cdot (1,0)_{x축} + b \cdot (0,1)_{y축}$으로 각 basis가 선형 결합되었음을 의미한다.

따라서 어떠한 좌표계에서 어떤 벡터를 나타내는 것은 해당 좌표계에서 정의된 축(basis)를 선형 결합하여 해당 벡터를 나타낼 수 있는 상수항들을 찾는 것이다. 또한 공간 상에는 여러 basis가 존재할 수 있으므로 다른 basis를 사용하여 같은 벡터를 표현할 수도 있으며(물론 선형 결합에 사용되는 상수항이 달라지므로 같은 벡터를 표현하더라도 수치는 달라진다), 이렇게 basis를 변환하는 것을 좌표계 변환으로 볼 수 있다.

2-2-3. Basis 변환

이제 어떻게 basis를 변환하여 좌표계를 변환할 수 있는 지 알아보자.

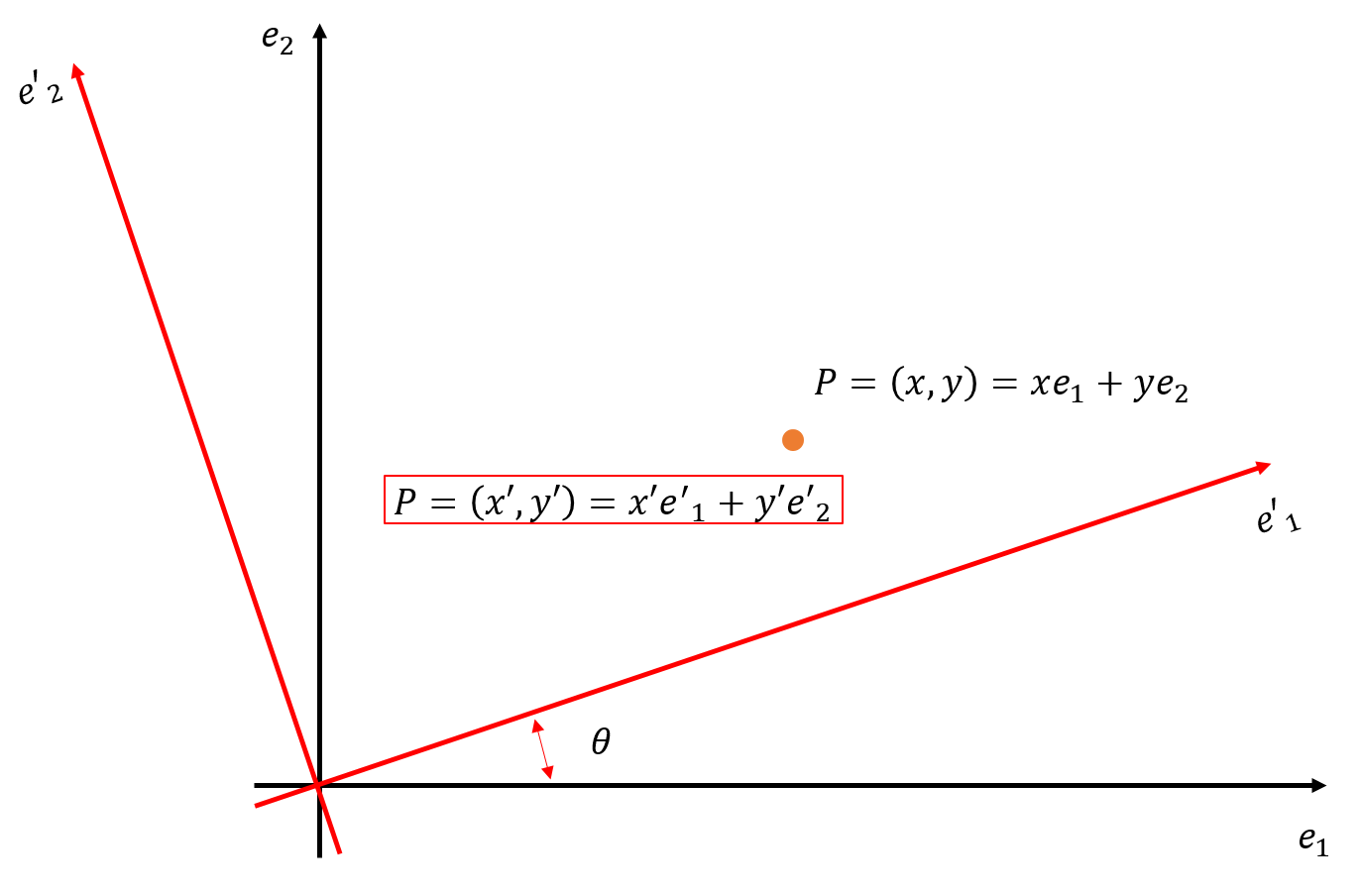
Figure 2. 좌표계의 회전변환

위의 그림에서 우리는 basis가 $e_1, e_2$인 좌표계에서 $(x,y)$로 나타나는 점 $P$를 basis가 $e_1' , e_2'$인 좌표계에 $(x',y')$으로 나타내고자 한다.

회전된 좌표계에서 점 $P$를 보면 다음과 같다.

• $P = (x',y') = x'e_1'+y'e_2' = \begin{pmatrix} \uparrow&\uparrow\\ e_1'&e_2'\\ \downarrow&\downarrow \end{pmatrix}\begin{pmatrix} x'\\ y' \end{pmatrix}$

이때 basis $e_1' , e_2'$는 $e_1, e_2$가 $\theta$만큼 회전변환 된 것으로 다음과 같다.

• $\begin{pmatrix} \uparrow&\uparrow\\ e_1'&e_2'\\ \downarrow&\downarrow \end{pmatrix}=\begin{pmatrix} \cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{pmatrix} \begin{pmatrix} \uparrow&\uparrow\\ e_1 & e_2\\ \downarrow&\downarrow \end{pmatrix}$

이는 위의 회전변환의 예시에서 쉽게 도출이 가능하며, 예를들어 $e=(1,0)\rightarrow(\cos\theta, \sin\theta)$이다.

이러한 결과들을 정리하면 다음과 같다.

즉 회전 행렬 $\mathbf{R}$을 곱하여 $e_1' , e_2'$ 좌표에서 $e_1 , e_2$ 좌표로, $\mathbf{R^{-1}}$을 곱하여 $e_1 , e_2$ 좌표에서 $e_1' , e_2'$ 좌표로 변환 할 수 있다.

선형 변환과 관련된 분야인 선형 대수학은 사실 매우 공부할 거리가 많지만, 지금은 이 정도로 정리하고 이후 필요한 내용은 그때마다 소개하려고 한다.