SLAM: 기초 컴퓨터 비전부터 visual&LiDAR SLAM까지

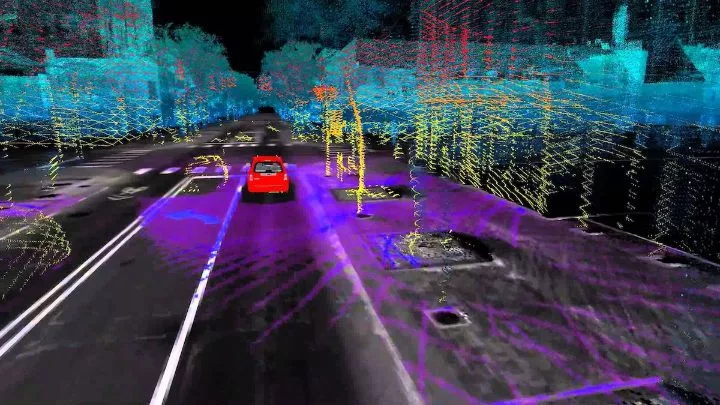
SLAM 시리즈 소개

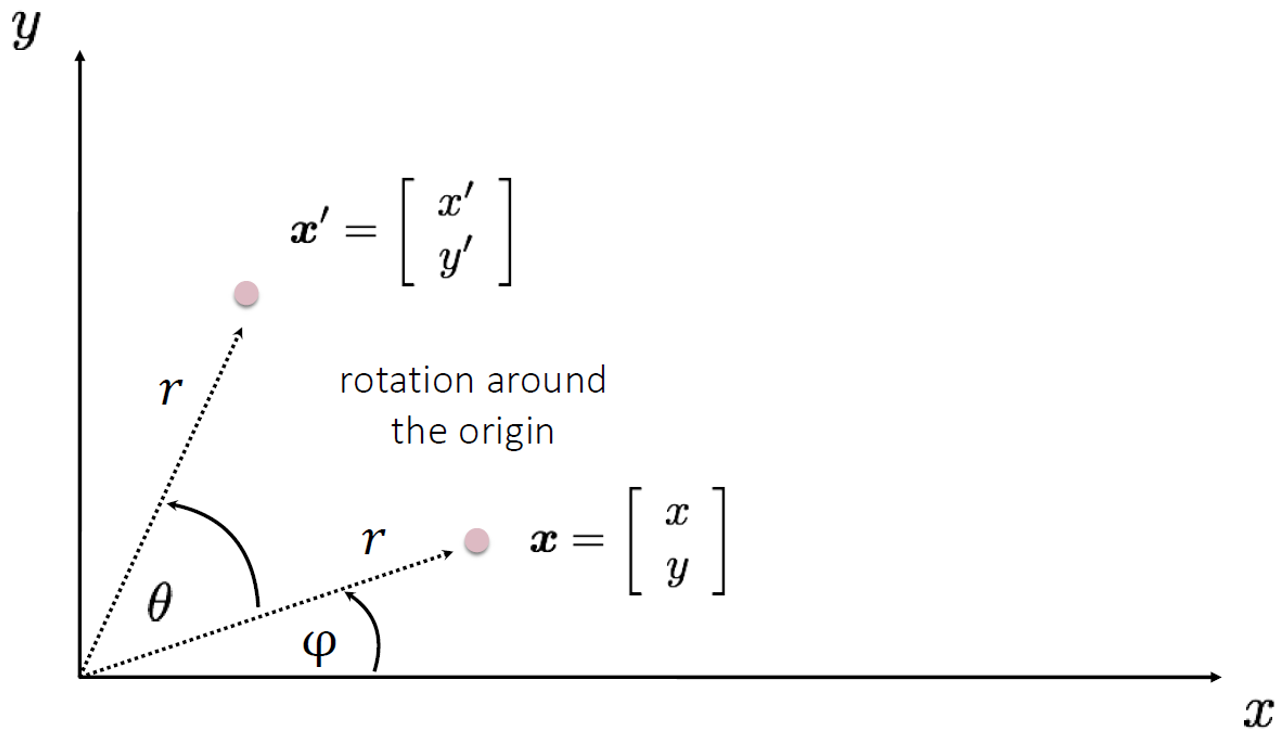
컴퓨터 비전 이해를 위한 기본 선형 변환 개념

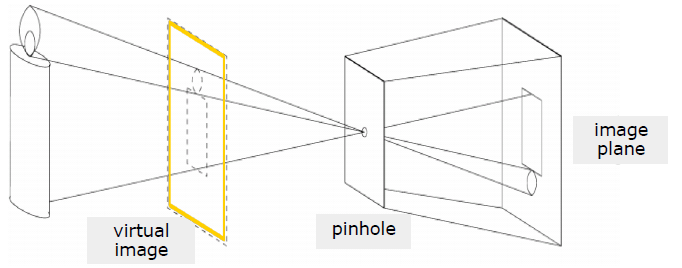
카메라 모델 및 homogeneous 좌표계 개념 설명

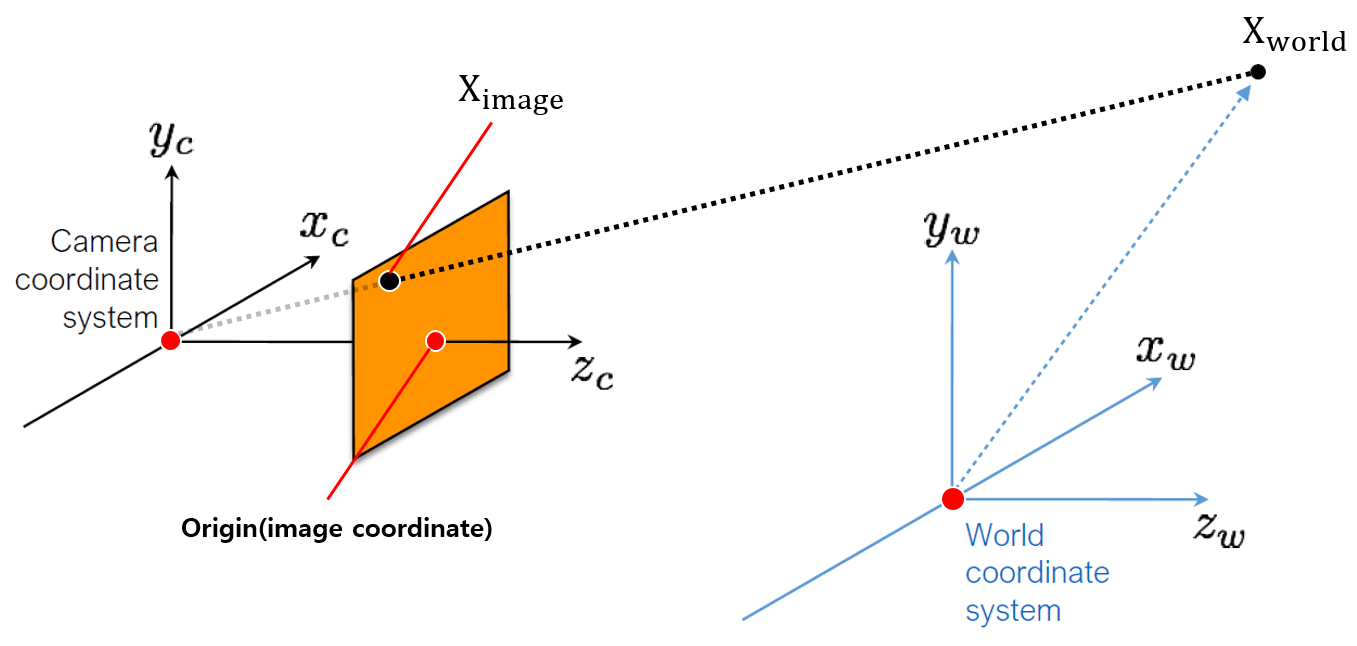
Image projection 과정과 이를 식으로 표현하기 위한 카메라 파라미터 개념

기초 선형대수

행렬 분해 1: LU 분해

행렬 분해 2: QR 분해

행렬 분해 3: SVD

행렬 분해 4: Cholesky 분해

켈리브레이션의 원리 등

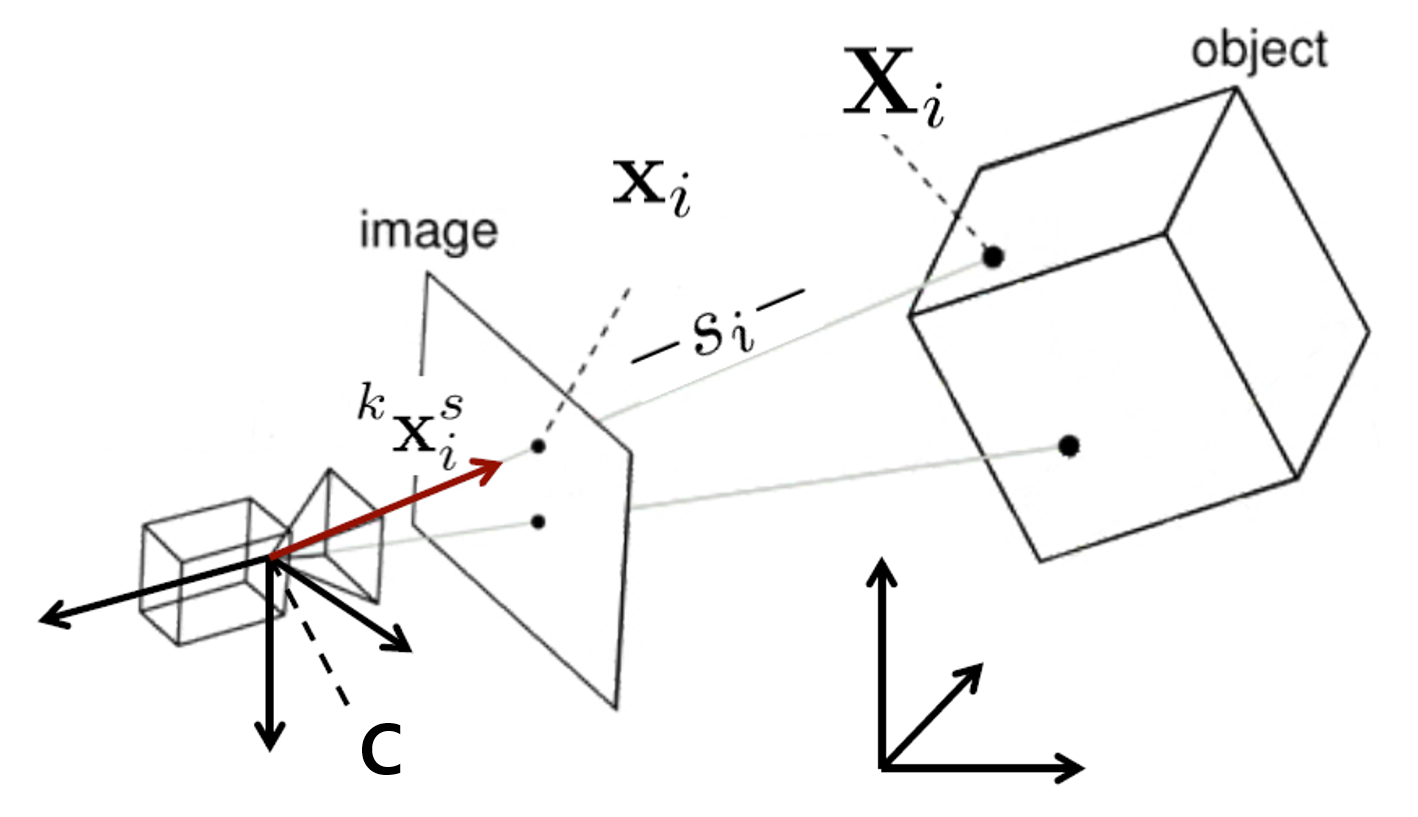
P3P 개념 및 원리

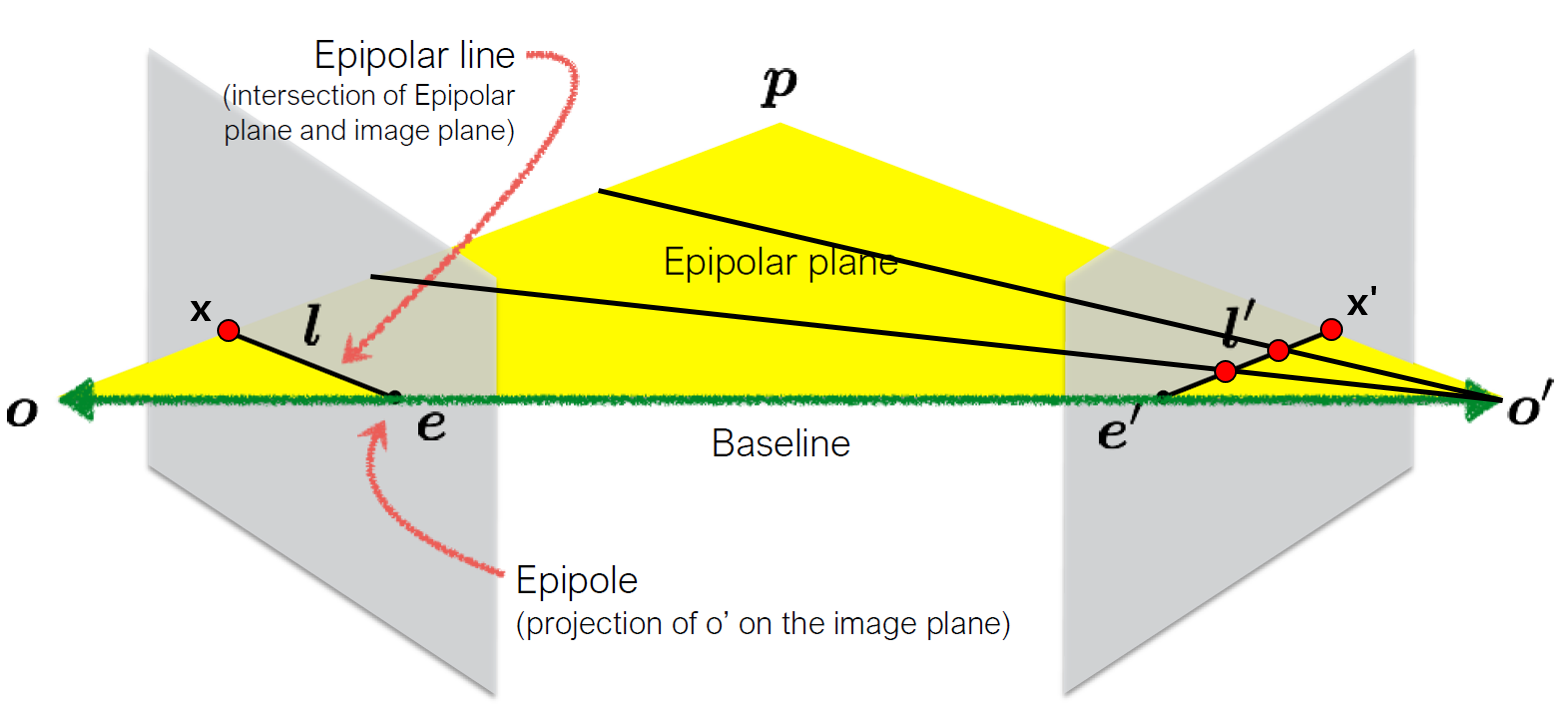
Epipolar 기하 개념 및 원리

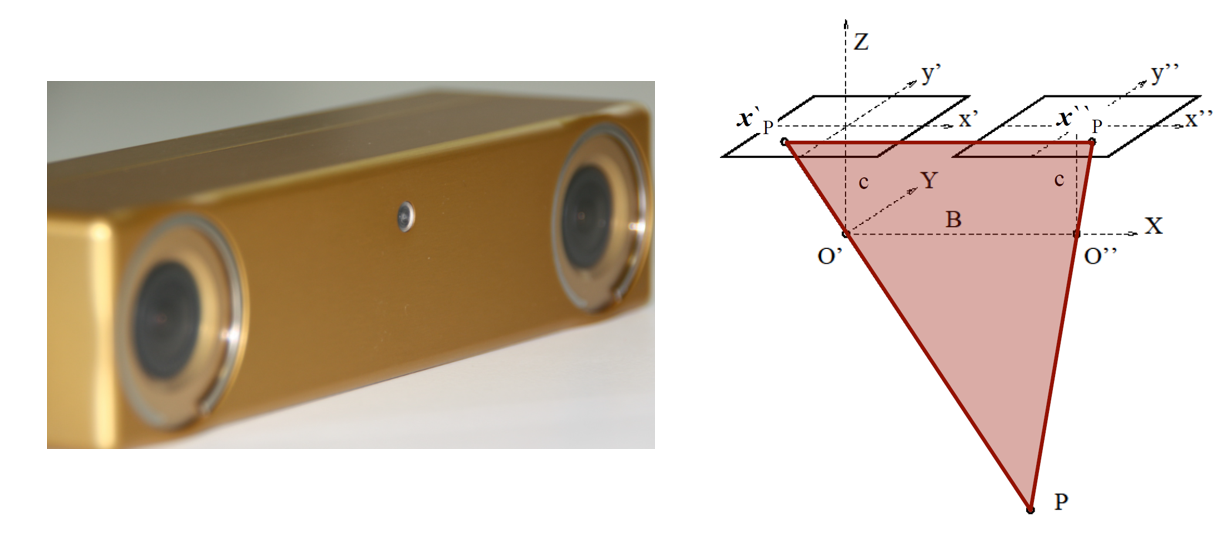
스테레오 비전 개념 및 원리

이미지 특징점, 매칭, 추적 방법 등

앞에서 우리는 회전 및 변환 행렬을 곱하여 어떤 점이나 좌표계를 transform하였다. 하지만 회전 행렬을 보면, $\mathbf{R} \sub SO(3)$이므로 직교행렬($\mathbf{R}^T\mathbf{R}=\mathbf{I}$) 및 $det(\mathbf{R

1. Group 군(group)이란 어떤 집합과 연산자로 이루어져 있으며, $G=(\cdot, A)$등과 같이 쓸 수 있고, 다음의 성질을 갖는다. 닫힘성(Closure): $\forall a, b \in A, a \cdot b \in A$ 결합성(Associativ

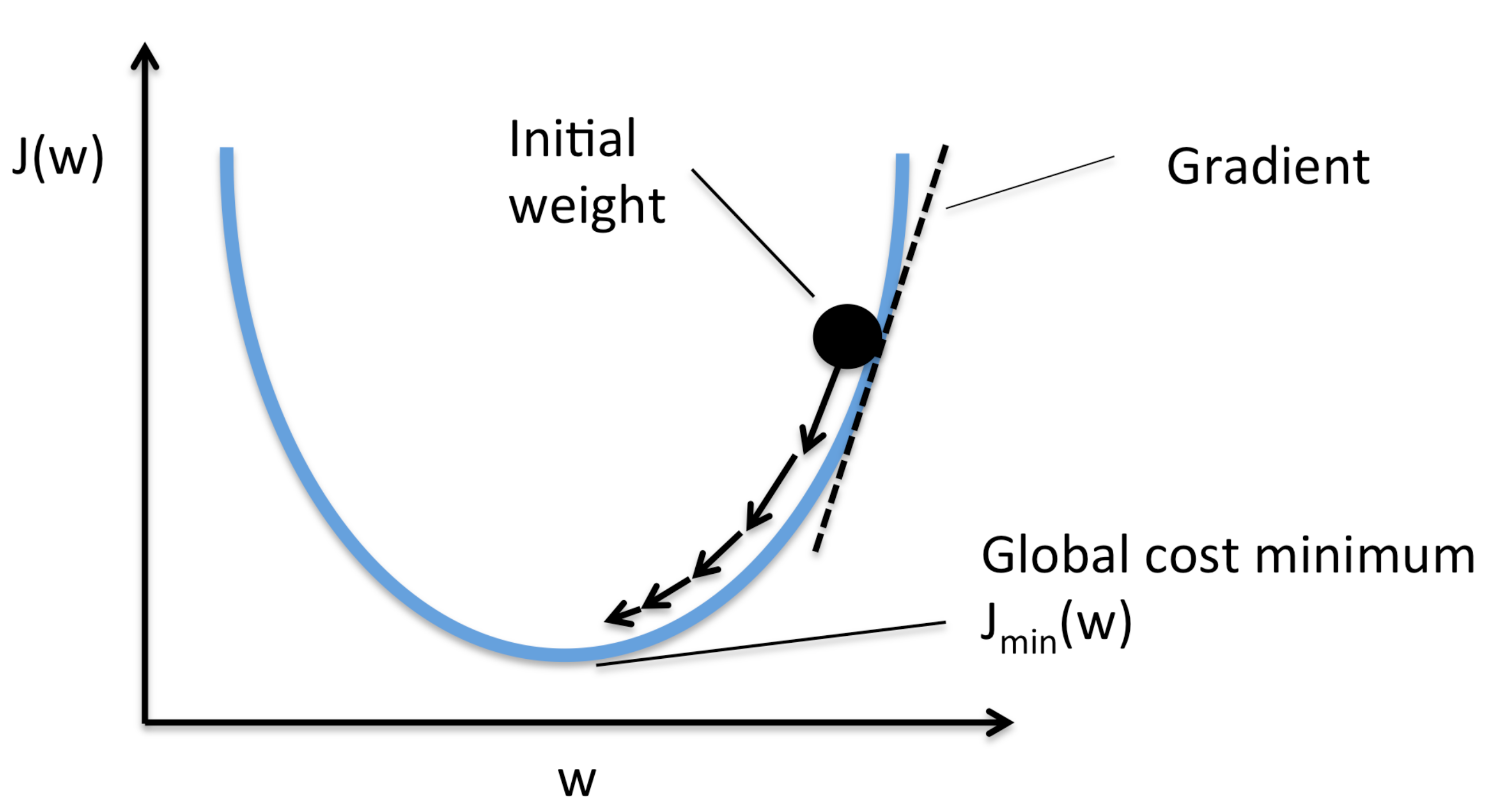
수치최적화 방법 소개(Gauss-Newton, LM 등)