Tracking 개요

고영민·2022년 12월 8일
Computer VisionMOT
0

다중 객체 추적

목록 보기
1/3

해당 포스트는 https://www.youtube.com/@multipleobjecttracking1226중 "Part 1: Introduction to Multiple Object Tracking (MOT)"의 내용을 기반으로 작성됨.

1. 개요


Figure 1. 다중 객체 추적(Multiple Object Tracking) 예시

객체 추적(Object Tracking)이란 말 그대로 움직이는 객체의 위치를 추적하는 것이다. 예를 들어, 컴퓨터 비전 분야에서 객체 검출기들이 RGB(0~255) 값으로 이루어진 이미지 하나를 입력받아 특정 객체의 위치를 알아내는 것과 달리 객체 추적기는 연속된 데이터를 입력 받아 그로부터 객체의 위치 등의 상태를 추정하게 된다. 이때 주어지는 데이터에는 어느정도의 noise가 섞여 있을 수 있으며, 여러가지 fliter 등을 통해 오차를 줄여가게 된다. 카메라, LiDAR, Radar 등 다양한 센서를 사용할 수 있다.

일반적으로 하나의 객체를 추적하게 되면 single object tracking 이라고 하고, 여러 객체를 동시에 추적하게 되면 multiple object tracking (MOT) 이라고 한다. 일반적으로 tracking을 어렵게하는 요소는 몇 가지가 있다.

  • 객체의 상태를 모름
  • 객체가 field of view(FOV) 밖으로 나가 센서 범위에서 사라질 수 있음
  • 새로운 객체가 FOV 안으로 들어올 수 있음
  • 한 객체가 다른 객체를 가릴 수 있음
  • 검출기가 잘못된 검출 결과를 줄 수도 있음 (일반적으로 객체 추적은 검출기 결과를 기반으로 동작하는 경우가 많음, 아래 내용 참고)
  • FOV 안에 존재하는 객체의 수를 모름

또한 MOT는 single object tracking 보다 계산량이 증가하여 실시간 시스템을 구축하고자 하는 경우 많은 최적화가 요구될 수 있다.

따라서 MOT 관련 분야에서는 위의 문제를 해결하여 성능을 높이고자 하는 연구가 많으며, 추가적으로 다수의 카메라에서 다수의 객체를 동시에 추적하는 훨씬 어려운 환경에 도전하는 연구 또한 활발히 이루어지고 있다.

2. Tracking 구조


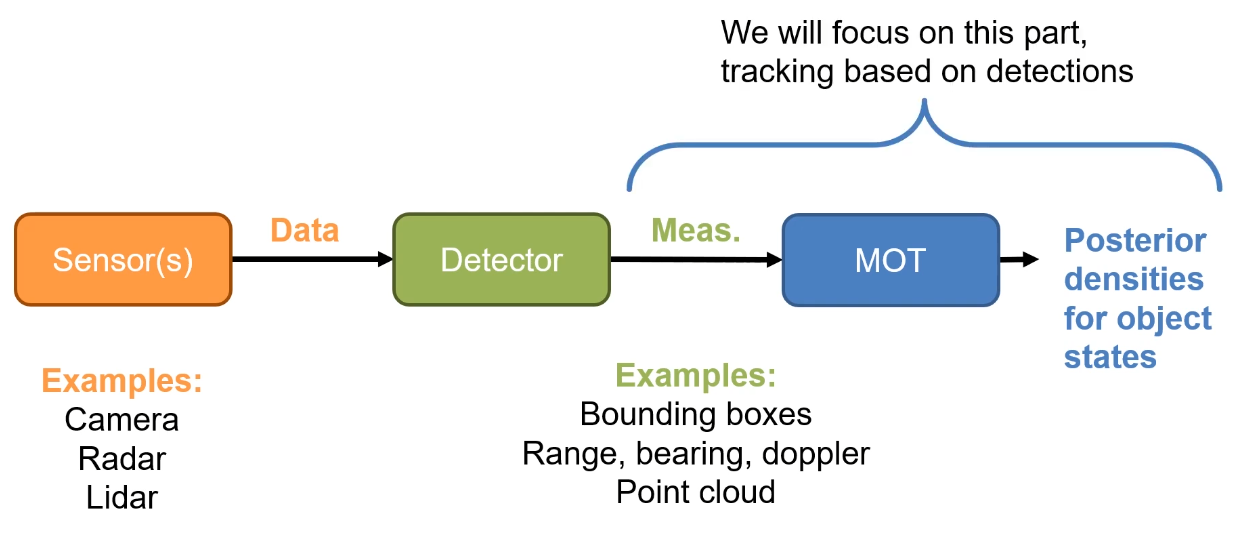
Figure 2. tracking by detection 구조

위의 tracking by detection 구조는 센서 데이터를 입력받아 검출기를 먼저 적용하고, 그 검출기 결과를 이용하여 object tracking을 수행하는 방법으로, 가장 많이 사용되는 tracking 방법이다. (물론 다른 구조도 있음)

카메라 영상을 이용하는 경우 검출기를 통해 객체의 bounding box(객체의 위치와 크기)를 찾아 추적기로 넘기며, 추적기에서는 과거의 경로를 바탕으로 위치를 보정하게 된다.

당연하게도 이러한 구조의 tracking 방법은 검출기 결과가 완벽하다는 가정을 하고 있기 때문에 검출기 성능에 많은 의존을 하게 된다. 따라서 검출기가 오작동하여 잘못된 위치를 결과로 주거나, 객체를 못 찾는 경우 tracking 결과 또한 잘못될 수 있으며, 이러한 문제를 해결하는 방향으로도 연구가 많이 진행된다. 또한 반대로 tracking 모듈은 과거의 경로를 바탕으로 검출기가 오작동 결과를 보정할 수 있는 능력이 있기 때문에 서로 상호보완 적인 모습을 보이기도 한다.

추가적으로 MOT 문제에서는 여러 개의 객체를 동시에 추적해야하기 때문에 한 장의 사진에 여러 객체가 동시에 등장하고, bounding box 결과 또한 여러 개가 나온다. 하지만 각 bounding box에는 보통 각 객체를 구분하는 ID 정보가 포함되어 있지 않으며, MOT에서는 각 객체별로 움직인 위치를 개별적으로 추적해야하기 때문에 bounding box 결과를 그대로 사용하지 못한다. 예를 들어 <figure 1>에서 보행자를 검출한 결과가 점으로 표시되는데, 일반적인 검출기에서는 해당 점들이 모두 "사람"이라는 class로 분류가 될 뿐이지 보행자 1, 보행자 2, ..., 보행자 n을 구분하지 못한다.

따라서 이전 프레임과 현재 프레임의 검출 결과를 보고 같은 instance 끼리 연관시켜주는 작업이 필요하며, 이를 data association 이라고 한다. 추가적으로 새로 나타난 객체나 잘못된 검출 결과를 지우는 작업 또한 함께 이루어지며, data association 또한 tracking 분야의 큰 연구 과제 중 하나이다.

3. Filter

필터는 보통 무엇인가를 순차적으로 걸러내는 것을 의미한다. 예를 들어 정수기를 보아도 물이 공급되면 여러 겹의 정수 필터를 지나며 점점 깨끗한 물이 된다.

수학적으로도 필터를 정의할 수 있다. 가장 간단한 평균 필터를 살펴보면, 보통 평균을 구한다고 하면 입력된 모든 수를 더하고 합계를 전체 입력 개수로 나누게 된다.

average=x1+x1+⋯+xNNaverage = \frac{x_1 + x_1 + \cdots + x_N}{N}

다만 이렇게 구할 경우 평균을 구하기 위해서 많은 수의 데이터를 저장하고 있어야 하는 등의 문제가 발생한다. 하지만 평균 필터를 사용하면 다음과 같이 재귀적으로 평균을 구할 수 있다.

ak=k−1kak−1+1kxka_k = \frac{k-1}{k}a_{k-1} + \frac{1}{k}x_k

위의 식에서 알 수 있듯이 단지 이전 step의 결과만 저장하고 있으면 평균을 구할 수 있고, k가 커질 수록 점점 실제 평균값에 가까워지게 된다.

객체 추적에서도 마찬가지이다. 순차적으로 들어오는 데이터(영상 및 bounding box)을 통해 실제 객체의 위치를 순차적으로 추론해야하며, 대표적으로 Baysian filter, Kalman filter 등이 있다 (링크). 이러한 필터들은 보통 prediction과 update 단계를 반복적으로 진행한다.

Prediction 단계에서는 아래와 같은 Chapman-Kolmogorov prediction 방법 등을 통해 이전 step까지의 추론 결과 및 관측치를 통해 현재 step의 상태를 추론한다. 이때 예시로 든 Chapman-Kolmogorov prediction 방법은 Markov 과정을 전제로 하며, step 1에서 k 까지의 과정을 1~(k-1)과 (k-1)~k 의 과정으로 쪼개어 생각한다.

p(xk∣z1:k−1)=∫p(xk∣xk−1)p(xk−1∣z1:k−1)dxk−1p(x_k | z_{1:k-1})= \int{p(x_k|x_{k-1})p(x_{k-1}|z_{1:k-1})}dx_{k-1}

이때 사용되는 p(xk∣xk−1)p(x_k|x_{k-1})가 운동 모델이며, 객체의 움직임을 모델링한 것이다. 예를 들어 차량을 추적하는 경우 가장 간단한 차량 모델인 bicycle model을 생각할 수 있다.

Update 단계에서는 관측치를 통해 prediction 단계의 추론 결과를 보정하며 다음과 같은 Bayes update를 예시로 들 수 있다.

p(xk∣z1:k)=p(zk∣xk)p(xk∣z1:k−1)p(zk∣zk−1)p(x_k | z_{1:k})= \frac{p(z_k|x_{k})p(x_{k}|z_{1:k-1})}{p(z_k|z_{k-1})}

또한 위의 내용을 조합해서 아래와 같이 likelihood를 계산할 수 있으며, 이를 최대화하는 등의 방법으로 data association 등을 수행할 수 있다.

p(zk∣z1:k−1)=∫p(zk∣xk)p(xk∣z1:k−1)dxkp(z_k | z_{1:k-1})= \int{ p(z_k|x_{k})p(x_{k}|z_{1:k-1}) dx_k }

Filter의 자세한 과정은 이후 내용에서 소개된다.

profile
고영민
다음 포스트

Single Object Tracking

0개의 댓글