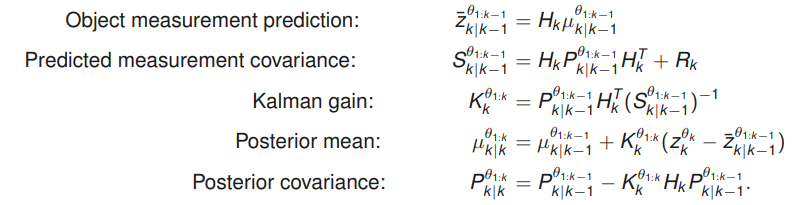해당 포스트는 https://www.youtube.com/@multipleobjecttracking1226중 "Part 2: Single Object Tracking in clutter"의 내용을 기반으로 작성됨.

1. 개요

여기서는 clutter가 발생하는 상황에서의 single object tracking(SOT)에 대한 내용을 소개한다. SOT는 MOT와는 달리 오직 하나의 객체만 등장하는 상황에서의 tracking 방법이며, 이로 인해 MOT 보다는 문제 설정을 간단하게 할 수 있다. 예를 들어, 객체의 숫자를 추정하거나 객체가 FOV를 들락날락하는 문제를 신경쓰지 않아도 되며, data association 또한 비교적 간단해진다. SOT에서 주로 신경써야하는 부분은 다음과 같다.

• 시간에 따른 state의 변화
• Noisy한 측정치
• Detection의 실패
• clutter의 검출
• Data association

여기서 clutter란 불필요한 에코 같은 것으로 예를 들어 레이더에서 관심 객체가 아닌 지면, 바다, 임의의 물체 등에 의해 마치 객체처럼 검출되는 부분을 의미한다. 따라서 실제 관심 객체에 의한 detection 결과와 clutter들이 섞여있을 경우(둘은 겉보기로 구분이 되지 않음) 어떻게 object의 위치를 추정하고 추적할 수 있을 지에 대한 내용이 소개된다.

2. 확률분포(Bernoulli, Binomial, Poisson)

뒤에서 이어질 내용에서 Bernoulli Binomial, Poisson 분포를 사용하여 센서의 측정 모델 등을 표현한다. 먼저 베르누이(Bernoulli) 분포의 경우 동전 던지기와 같이 binary로 확률변수 $X$가 $X=0$ 또는 $X=1$의 결과만 특정 확률($\mu$)에 따라 나오는 분포이다. 따라서 다음과 같이 $\mu$라는 모수(parameter)로 정의된다.

이항(Binomial) 분포의 경우 위와 같은 베르누이 시행을 N번 수행했을 때, 성공한 횟수를 확률 변수 $X$로 두어 몇 번 성공할 지에 대한 확률 값을 얻을 수 있는 분포이다. 따라서 다음과 같이 N과 $\mu$를 모수로 두어 정의할 수 있다.

푸아송(Poisson)분포는 발생 확률이 매우 적은 이항 분포 시행을 매우 많이 수행했을 때의 분포이다. 정해진 시간(또는 공간)에서 어떤 사건이 일어날 횟수에 대한 기댓값을 $\lambda$로 두었을 때 해당 사건이 $n$회 일어날 확률을 얻을 수 있으며, 다음과 같이 $\lambda$를 사용하여 정의할 수 있다.

3. SOT with known associations

우선 clutter가 없고 object만 존재하는 간단한 환경에서의 SOT를 수행한다. SOT의 목표는 시간에 따라 연속적으로 취득되는 센서 데이터를 통해 관심 객체의 위치를 예측 및 추정하는 것으로, 이를 위하여 앞선 글에서 설명했던 filter를 사용한다. 간단한 Bayes filter는 다음과 같다.

먼저 prediction 과정을 살펴보면, 오른쪽 항에서 $p(x_{k-1}|Z_{1:k-1})$는 이전 step의 결과이므로 이미 가지고 있고, $p(x_k|x_{k-1})$만 구하면 된다. $p(x_k|x_{k-1})$는 객체의 motion model이라고 하여 객체가 $k-1$의 시점에서 $x_{k-1}$에 있었을 때, 다음 번 k번째 시점에서 어디에 있을 지에 대한 것을 모델링 한 것이다. 이러한 motion model은 보통 $\pi(x_k|x_{k-1})$로 표현하며, linear 모델에서는 다음과 같이 Gaussian 분포로 모델링하는 경우가 많다.

따라서 prediction 과정을 motion 모델을 대입하는 것으로 수행되며, 자세한 계산은 motion model에서 사용되는 식과 확률 분포에 따라 달라지지만 위와 같이 Gaussian 분포를 사용한 linear 모델을 사용할 경우에는 Kalman 필터의 계산을 참고 할 수 있다(링크).

다음으로 update 과정을 살펴보면, 분모의 $p(Z_k|Z_{k-1})$는 우리가 관심있어하는 변수인 $x$와 관련이 없는 식이므로 normalize term으로 둘 수 있다. 또한 $p(x_{k}|Z_{1:k-1})$는 prediction 단계의 결과이고, 따라서 $p(Z_k|x_{k})$만 구하면 된다. 이는 객체의 위치가 주어졌을 때 객체에 측정되는 measurement matrix를 모델링한 것이다. 예를 들어 객체가 FOV 안에 있어도 센서의 해상도 등의 문제로 검출이 안될 수도 있으며, 객체가 없더라도 잘못된 검출이 발생할 수도 있고, 노이즈로 인해 정확한 위치보다 약간 다른 곳을 출력할 수도 있다. 지금은 clutter가 없는 환경을 가정하므로 $Z$대신 $O$를 써서 표현한다.

만약 객체가 검출되지 않았다면 measurement matrix $O_k$에는 아무 값도 없을 것이고, 검출되었다면 $O_k$는 센서가 측정한 객체의 위치 $o_k$가 들어있을 것이다. 단일 객체 추적을 가정하고 있으므로 $\mid O_k \mid$는 0 또는 1이며, 따라서 $\mid O_k \mid$를 다음과 같이 검출될 확률 $P^D(x_k)$를 사용하여 베르누이 분포로 표현할 수 있다.

이를 이용하면 다음과 같이 쓸 수 있다.

여기서 $g_k(o_k|x_{k})$는 센서의 특성을 나타내는 식으로 센서의 measurement model이라고 하며, 객체가 $x_{k}$에 있을 때, 센서가 반환하는 객체의 위치(측정값) $o_k$에 대한 확률이다. 위에서 대문자 $O$를 사용하는 이유는 $O_k$가 측정값 $o_k$들의 집합이기 때문이며, MOT를 하거나 clutter가 존재하는 경우에는 1개가 아닌 여러 개의 값이 들어가게 된다.

Prediction 단계와 마찬가지로 measurement model은 Gaussian을 이용한 linear 식으로 표현될 수 있으며, 이 경우 또한 Kalman fliter와 같이 계산된다.

4. Clutter Model

이제 clutter가 존재한다고 가정하여 SOT를 수행하기 위해 clutter에 대한 측정값 모델링을 수행한다. clutter를 포함한 measurement matrix는 다음과 같이 쓸 수 있다.

여기서 $C_k$는 clutter에 대한 측정값 $c_k$들이 들어있는 matrix이며, $\Pi$는 column vector를 무작위로 섞었다는 뜻이고, 즉, $O_k, C_k$가 섞여서 어떤 것이 관심 객체에 대한 측정값인지 알 수 없다는 의미이다.

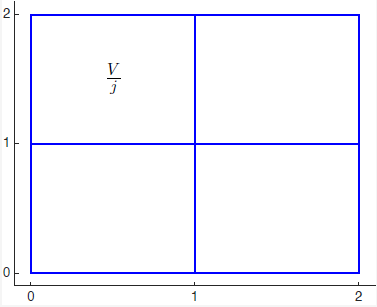
Figure 1. 간단한 센서 grid

보통의 센서는 특정한 FOV와 해상도를 가지고 있으며, 해상도에 따라 최대로 검출할 수 있는 객체의 수나 정확도가 달라진다. 예를 들어 Fig 1에서는 2x2 ($=V$)의 FOV를 가지고 있고, 4개($=j$)의 cell을 통해 측정하여 최대 4개의 값만이 출력된다.

따라서 clutter $C_k = \Pi (C^{(1)}_k, \cdots, C^{(j)}_k)$로 쓸 수 있고, $C^{(i)}_k$는 $i$번째 cell에서 관측된 clutter이다. 각 $C^{(1)}_k, \cdots, C^{(j)}_k$는 독립적이라고 가정하고, 단위 면적 당 검출되는 clutter의 숫자에 대한 기대값을 $\lambda$라고 할 때, $\mid C^{(i)}_k \mid$는 확률 $\lambda V/j$를 가지는 베르누이 분포를 따른다. 그리고 하나의 셀에서 객체가 검출되었을 때, 그 위치에 대한 측정값은 uniform distribution을 따른다.

하지만 여기서는 센서 해상도에 제한을 두지 않으며, 이는 $j$가 매우 크다는 의미이다. 따라서 $\mid C_k \mid$는 $E[\mid C_k \mid] = V\lambda$로 정의되는 푸아송 분포를 따르며, $C_k$는 Poisson point process(PPP)를 통해 결정된다.

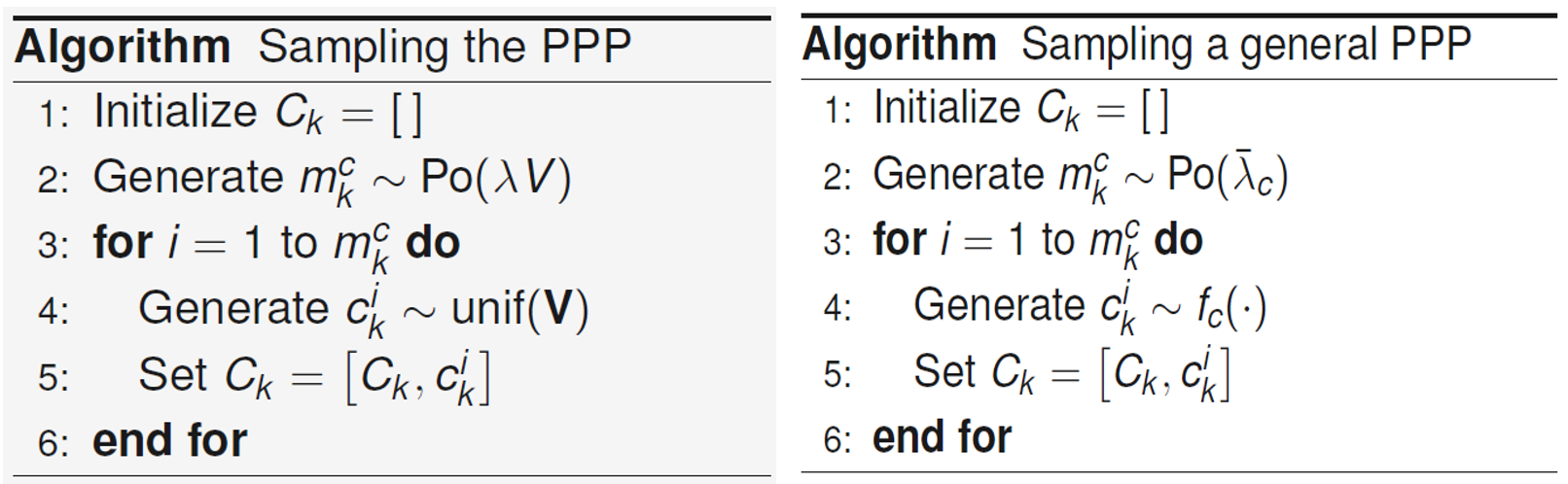
Figure 2. Poisson point process(PPP)를 통한 측정값 샘플링

이때 $C_k$ 특성은 다음과 같다. Clutter의 갯수는 $m^c_k \sim Po(\lambda V)$와 같이 푸아송 분포를 따르고, $C_k$에 들어있는 관측값들 $c^1_k, \cdots, c^{m^c_k}_k$들은 i.i.d.이고 $c^i_k \sim unif(V)$이다.

보통 PPP는 intensity function $\lambda_c(c) \ge 0$ 또는 $\bar{\lambda}_c = \int \lambda_c(c) dc$로 표현되는 rate와 $f_c(c) = \frac{\lambda_c(c)}{\bar{\lambda}_c}$로 표현되는 spatial pdf로 parameterize된다. 여기서 두 parameterize 방식 사이에 $\lambda_c(c) = \bar{\lambda}_c f_c(c)$의 관계가 있음을 알 수 있다. 각 파라미터의 의미는 fig 2에서 알 수 있다.

이제 이러한 clutter 모델을 사용하여 $p(Z_k|x_{k})$를 찾고 clutter가 있는 환경에서의 update 과정을 수행할 수 있다. 이때 문제가 되는 점은 $Z_k$의 길이가 무작위하고, 어느 값이 관심 객체에 의한 검출값인지 모른다는 것이다. 이를 해결하기 위하여 data association 과정이 추가되며, 이는 다음과 같이 표현되어 어떤 측정값이 관심 객체에 대한 것인지 표시한다.

그리고 $p(Z|x)$를 계산하기 위하여 다음과 같이 추가적인 변수 $m, \theta$를 이용하여 식을 변형한다.

여기서 첫번째 줄에서는 관측치의 갯수 $m$이 추가되었는데 이는 이미 $Z$에 포함된 정보이므로 확률값에 변화를 주지 않는다. 그리고 두번째 줄에서는 data association $\theta$가 추가되었고 전체 확률 정리가 사용되었으며, 세번째 줄에서는 결합확률과 조건부확률의 성질이 사용되었다. 위와 같이 주어진 식을 $p(Z|m, \theta, x)$와 $p(\theta, m|x)$로 표현하는 이유는 두 식이 closed form으로 표현될 수 있기 때문이다.

해당 closed form을 구하기 위하여 먼저 두가지 경우를 각각 생각한다. 먼저 $\theta=0$인 경우이며, 이는 object가 검출되지 않고 m개의 clutter만 검출된 경우이다. Fig 2를 보면 각 clutter, $z^i$의 측정값은 $f_c$에 따라 sampling 됨을 알 수 있으며, 따라서 $Z$에 대한 확률을 다음과 같이 각 $z^i$에 대한 확률의 곱을 표현할 수 있다.

그리고 $p(\theta, m|x)$는 object가 검출되지 않고, $m$은 푸아송 분포를 따른다는 점에서 다음과 같이 쓸 수 있다.

이 두 식을 합치면 다음과 같다.

다음으로 $\theta \ne 0$인 경우이며, $z^i$중에서 $i=\theta$만 관심객체에 의한 것이고 나머지는 clutter이므로 다음과 같이 쓸 수 있다.

이때, $p(\theta, m|x)$에서 $m$으로 나누어주는 이유는 $\theta$가 가질수 있는 수가 $m$가지이기 때문이다.

위의 두 식을 합치면 다음과 같다.

두 결과를 사용하여 다음과 같이 쓸 수 있다.

이제 이를 이용하여 update를 수행할 수 있고, 만약 $Z$가 비어있다면(측정치가 하나도 없을 때) update 과정은 생략한다.

5. Data Association Hypotheses

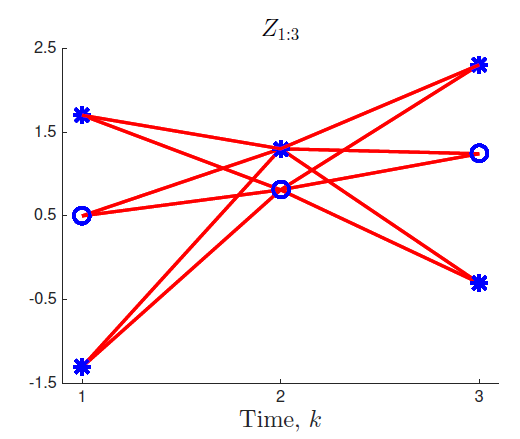
Figure 3. Data association에 따른 tracking hypotheses, 원이 관심 객체이며, 별은 clutter이지만, 컴퓨터는 어떤 것이 객체인지 모르기 때문에 모든 경우의 수를 계산해보아야 한다.

이제까지 내용을 바탕으로 SOT를 수행해보자. 위 그림처럼 컴퓨터는 어떤 것이 객체인지 모르기 때문에 모든 경우의 수를 계산해보아야 하고, 따라서 data association에 의한 hypotheses가 posterior $p(x_k|Z_{1:k})$를 계산하기 위해 고려되어야 한다. 전체 확률의 정리를 이용하면 다음과 같다.

즉, posterior $p(x_k|Z_{1:k})$는 여러 hypotheses에 의해 정의되는 분포가 중첩되어 있는 것으로, 우선 이를 일반화하여 계산해본다. 어떤 확률분포 $p(x)$는 여러 $\theta$에 의해 정의되는 $m_\theta(x)$의 중첩으로 다음과 같이 표현할 수 있다.

이때, 각 $m_i(x)$는 $0 \lt \int{m_i(x)dx} \lt \infin$를 만족한다. 이때 어떤 상수 $c$를 도입하면 $p(x) \propto m(x) \rightarrow p(x) = cm(x)$로 쓸 수 있고, $p(x)$는 확률분포이므로 다음과 같이 쓸 수 있다.

여기서 주목해야하는 점은 어떤 함수 $m(x)$를 $\int m(x') dx'$로 나누었더니 확률 분포 $p(x)$가 되도록 normalize 되었다는 점이다. 이러한 성질을 사용하여, $\tilde{w}_\theta = \int m_\theta(x) dx$를 사용하면 다음과 같이 각 $m_\theta$를 확률분포로 표현할 수 있다.

이를 이용하여 다음과 같이 쓸 수 있다.

이때, $\int m(x) dx = \sum^{m}_{\theta=0} \int m_\theta(x) dx = \sum^{m}_{\theta=0} \tilde{w}_\theta$ 임을 사용하면 다음과 같이 쓸 수 있고, 이는 어떤 확률 분포를 다른 여러 확률 분포의 weighted sum으로 표현할 수 있다는 것을 의미한다.

이제 posterior $p(x|Z)$를 위와 같이 여러 확률 분포의 합으로 표현해보자.

$\tilde{w}_\theta = \int m_\theta(x) dx = p(Z,m,\theta) = p(Z,\theta)$이고 $w_\theta = \tilde{w}_\theta /\sum^{m}_{i=0} \tilde{w}_i = p(Z,\theta)/p(Z) = p(\theta|Z)$이다. 비슷한 방법으로 $p_\theta(x)$를 구하면 $p_\theta(x)=p(x|\theta, Z)$가 된다.

이제 앞에서 구했던 $p(Z|x)$ 모델을 적용해 update를 수행해보면 다음과 같다. 이때, 우리는 $m_\theta(x)$를 정의하는 것이 목표이므로 $x$가 포함되지 않은 term은 상수로 생각할 수 있다. 그리고 앞에서

$\theta = 0$일 경우, $\tilde{w}_0$와 $p_0(x)$는 다음과 같이 정의된다.

$\theta \ne 0$일 경우, $\tilde{w}_\theta$와 $p_\theta(x)$는 다음과 같이 정의된다.

그리고 $w_\theta \propto \tilde{w}_\theta$에서 $w_\theta$를 구할 수 있다.

6. Conceptual Solution

앞에서는 여러 개의 hypotheses들을 계산하여 posterior를 update하는 방법을 살펴보았다. 여기서는 time step $k$까지 추가하여 완전한 형태의 prediction, update step을 계산해본다. 이때, 계산을 간소화하기 위하여 몇가지 가정을 한다. Prior density $p(x)$와 motion, measurement model는 linear Gassian으로 주어지고, 검출 확률 $P^D$는 특정 상수로 주어진다. 우리는 이전 step의 update 결과를 다음과 같이 쓸 수 있다.

여기서 $\theta_{1:k} = (\theta_{1}, \cdots, \theta_{k})$는 data association hypotheses의 나열이며, summation 기호는 다음을 의미한다.

이제 prediction step을 살펴보자.

위에서 3번째 줄에서는 $p^{\theta_{1:k-1}}_{k-1|k-1}(x_{k-1})$의 정의식을 대입해보면 알 수 있으며, prediction 단계가 지나더라도 weight가 변화하지 않았고, 각 hypothesis마다 prediction이 수행된 형태라는 것을 알 수 있다. 여기서 각 모델들이 linear Gassian이라면 Kalman filter를 사용하여 실제 계산을 수행할 수 있다.

$x_k = F_{k-1}x_{k-1} + q_{k-1}, \;\; q_{k-1} \sim N(0,Q_{k-1})$로 주어지면 motion model은 $\pi(x_k|x_{k-1})=N(x_k;F_{k-1}x_{k-1}, Q_{k-1})$이고, 이전 stpe의 식 $p^{\theta_{1:k-1}}_{k-1|k-1}(x_{k-1})$ 또한 Gaussian으로 $p^{\theta_{1:k-1}}_{k-1|k-1}(x_{k-1}) = N(x_{k-1};\hat{x}^{\theta_{1:k-1}}_{k-1|k-1}, P^{\theta_{1:k-1}}_{k-1|k-1})$와 같이 주어진다면, 위의 2번째 줄에서 행해지는 적분식은 Kalman filter의 과정과 같이 구할 수 있으며, 결과는 다음과 같다.

이제 update step을 살펴보자.

위의 식은 앞에서("5. Data Association Hypotheses") 수행했던 posterior update와 비슷한 과정으로 구할 수 있다(measurement model 도입 및 $\theta=0$과 $\theta\ne0$의 경우 구분). 여기서 $p(x_{k}|Z_{1:k}) = \sum_{\theta_{1:k}} w^{\theta_{1:k}} p^{\theta_{1:k}}_{k|k}(x_{k})$의 형식을 맞추기 위하여 각각을 구해보면 다음과 같다.

여기서 각 모델들이 linear Gassian이라면 Kalman filter를 사용하여 다음과 같이 실제 계산을 수행할 수 있다. $p^{\theta_{1:k-1}}_{k|k-1}(x_{k-1}) = N(x_{k};\mu^{\theta_{1:k-1}}_{k|k-1}, P^{\theta_{1:k-1}}_{k|k-1})$, $g_k(o_k|x_k) = N(o_k;H_kx_k,R_k)$로 주어진다면 다음과 같다(이때, 일반적인 관측치 $z$에 대한 measurement model이 아닌 관심 객체 검출에 대한 식 $g_k(o_k|x_k)$가 주어지는 이유는 각 data association hypothesis가 주어지고 해당 hypothesis 객체라고 생각한 후 계산하여 모든 경우를 합하기 때문이다).

위의 식을 구하는 Kalman filter update 과정은 다음 그림에서 찾을 수 있다.

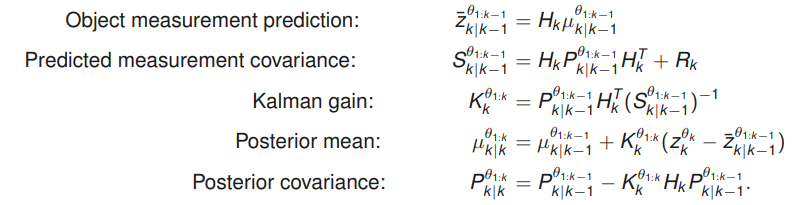
Figure 4. Kalman filter update 과정

7. 다른 SOT 알고리즘

위에서 SOT를 위한 prediction과 update 과정을 계산해보았지만, 한가지 문제점이 존재한다. 이는 연산량에 관련된 것으로 $k$가 커짐에 따라 hypotheses가 다음과 같이 급격히 증가하고, 모든 hypotheses에 대해 계산을 수행하는 위 알고리즘은 작동하기 어려워진다.

문제를 해결하기 위하여 pruning 또는 merging을 수행하는 다양한 SOT 알고리즘이 개발되어 왔다. 여기서 pruning이란 작은 weight를 갖는 hypotheses를 제거하는 것이고, merging은 여러 개의 density를 하나의 density로 근사하여 결합하는 것을 의미한다.

이러한 방법을 사용하는 알고리즘에는 다음과 같은 예를 들 수 있다.

• Nearest neighbour (NN) filter (pruning): 가장 높은 확률의 hypothesis를 제외하고 나머지는 제거함
• Probabilistic data association (PDA) filter (merging): 여러 분포가 중첩된 posterior를 같은 mean과 covariance를 갖는 하나의 Gaussian 분포로 근사
• Gaussian sum filter (GSF) (pruning/merging): 여러 분포가 중첩된 posterior를 높은 확률을 갖는 소수의 hypothesis에 해당하는 Gaussian 분포를 합하여 근사
• Gating: 높은 $P^D$, 작은 $\lambda_c$, 매우 큰 FOV를 갖는 이상적인 센서를 사용할 경우 weight에 특정 threshold를 두어 이 보다 작은 weight를 갖는 detection 결과를 모두 무시