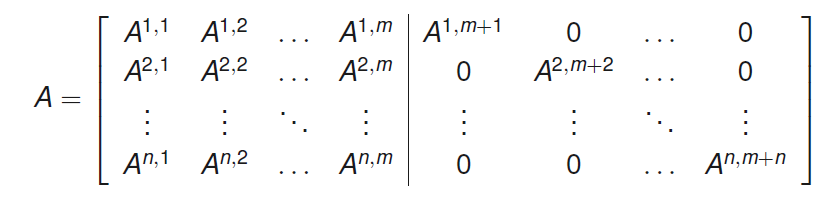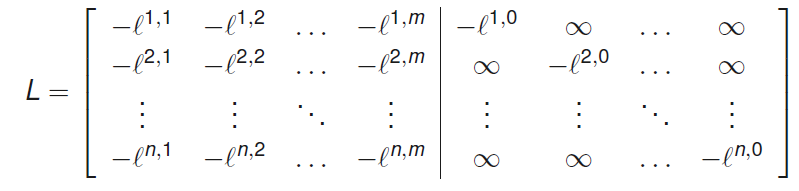Tracking a Known Number of Objects in Clutter

고영민·2023년 3월 27일

다중 객체 추적

목록 보기

3/3

해당 포스트는 https://www.youtube.com/@multipleobjecttracking1226중 "Part 3: Tracking a known number of objects in clutter"의 내용을 기반으로 작성되었으며, 해당 영상은 본 글에서 생략된 다양한 visualization 자료가 포함되어 있음.

1. 개요

이전 글에서는 관심 객체가 하나만 등장하는 SOT를 수행했지만, 이번 글에서는 관심 객체가 n개 등장하는 상황에서 다수의 객체를 동시에 추적하는 방법을 살펴본다. 일반적인 MOT와는 달리 n의 값을 알고있다고 가정한다. 관심 객체가 여러 개 존재하기 때문에 SOT보다 data association 등이 좀 더 복잡해진다.

Figure 1. 이번 글에서 다루는 환경의 예시

n개의 객체가 있다고 가정하기 때문에 state에 대한 prior는 $p(X_0) = p(x_0^1, \cdots, x_0^n )$ 과 같이 쓸 수 있고, 여기서는 n개의 객체가 모두 독립적이라고 가정하여, 다음과 같이 쓸 수 있다.

\begin{aligned} p(X) & = p(x^1, \cdots, x^n ) \\ & = \prod^n_{i=1}{p^i(x^i)} \end{aligned}

그리고 만약 확률 분포가 여러 분포의 합으로 이루어진 mixture density라면 다음과 같이 쓸 수 있다.

\begin{aligned} p(X) & = \sum_h w^h \prod^n_{i=1}{p^{i, h}(x^i)} \end{aligned}

2. Modeling the Mearsurements

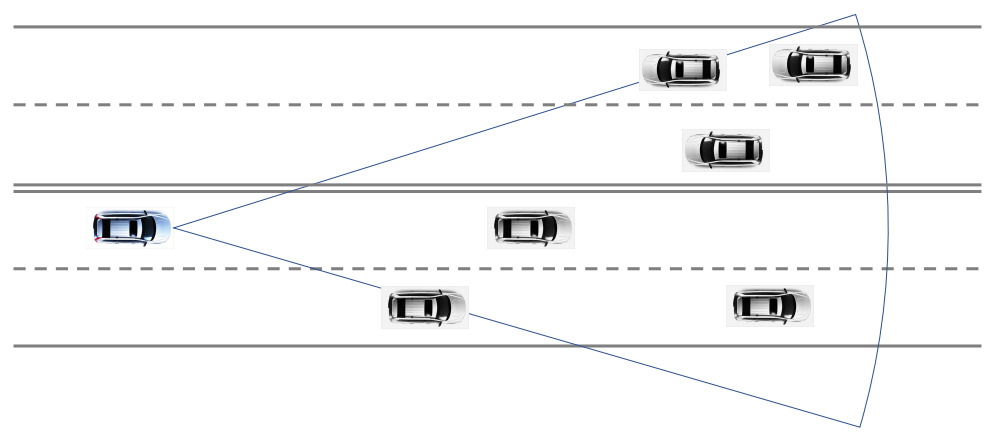
우선 여러 객체가 있을 때의 data association 표현을 알아보자. SOT 때과 비슷하지만, 몇 가지 추가되는 조건이 생긴다. 먼저 기본적으로 data association $\Theta_k$ 는 시점 $k$ 에서의 valid association $\theta_k$ 의 집합이며, association $\theta_k$ 는 다음과 같이 n개의 객체 각각에 associate 되는 측정값의 index로 표현된다.

\theta^i_k = \begin{cases} j \;\;\;\;\;\; if \; object \; i \; associated \; to \; measurement \; j\\ 0 \;\;\;\;\;\; if \; object \; i \; is \; undetected \end{cases}

\theta_k = [ \theta^1_k , \cdots , \theta ^n_k ]

예를 들어 객체가 2개 $X=[x^1, x^2]$ , 측정값이 2개 $Z=[z^1, z^2]$ 일 때, $\theta =[\theta^1. \theta^2] = [2,0]$ 이라면, 1번 객체는 $z^2$ 에 연관되고, 2번 객체는 관측되지 않았다는 의미이다.

객체를 측정값 $z$ 에 연관시키는 것이기 때문에, $\theta^i_k \in \{0, \cdots, m_k \}$ 이며( $m_k$ 는 측정값의 개수), 서로 다른 객체에 대한 association 값은 0일 때를 제외하고 같은 값을 갖지 않는다(즉, 두 객체가 동일한 측정값과 연관되지 않는다, the point object assumption). 또한 $m_k^c = m_k - m_k^o$ 이다.

이를 이용하여 우리는 필터의 업데이트 단계를 위한 measurement likelihood, $p_{Z|X}(Z|X)$ 를 구해야 한다.

p_{Z|X}(Z|X) = \sum_{\theta \in \Theta}p_{Z, \theta|X}(Z,\theta|X) = \sum_{\theta \in \Theta}p_{Z|X, \theta, m}(Z|X, \theta, m)p_{\theta, m|X}(\theta, m|X)

여기서 나타나는 각 term을 풀어쓰면 다음과 같다.

\begin{aligned} p_{\theta, m|X}(\theta, m|X) & = \underbrace{\prod_{i:\theta^i_k=0}{(1-P^D(x_k^i))}\prod_{i:\theta^i_k\ne0}{P^D(x_k^i)}}_{(1)} \underbrace{Po(m^c|\bar{\lambda_c})}_{(2)} \underbrace{\frac{1}{ \begin{pmatrix} m\\ m^o \end{pmatrix}m^o! }}_{(3)} \\ & = \frac{m^c!}{m!}Po(m^c|\bar{\lambda_c})\prod_{i:\theta^i_k=0}{(1-P^D(x_k^i))}\prod_{i:\theta^i_k\ne0}{P^D(x_k^i)} \end{aligned}

(1)은 $m^o$ 개의 객체에 대해서 association을 통해 주어지는 특정 집합의 검출 확률이며, (2)는 $m^c = m - m^o$ 개의 clutter 검출 확률, (3)은 특정 association set이 선택될 확률(여기서는 $m$ 개의 측정치 중 $m^o$ 를 선택하는 가짓수로 나눔)이다.

그리고 각 측정치가 독립적이라고 가정하면, 나머지 term은 다음과 같이 쓸 수 있다. 첫번째 term은 PPP에서의 spatial pdf, g는 measurement model이다.

p_{Z|X, \theta, m}(Z|X, \theta, m) = \prod_{j: \nexists \theta^i=j}{f_c(z^j)}\prod_{i: \theta^i\ne0}{g(z^{\theta^i}|x^i)}

이 두 식을 결합하여 정리하면 다음과 같다.

\begin{aligned} p_{Z|X}(Z|X) & = \sum_{\theta \in \Theta}p_{Z, \theta|X}(Z,\theta|X) = \sum_{\theta \in \Theta}p_{Z|X, \theta, m}(Z|X, \theta, m)p_{\theta, m|X}(\theta, m|X) \\ & = \sum_{\theta \in \Theta}\left[ \prod_{j: \nexists \theta^i=j}{f_c(z^j)}\prod_{i: \theta^i\ne0}{g(z^{\theta^i}|x^i)} \frac{m^c!}{m!}Po(m^c|\bar{\lambda_c})\prod_{i:\theta^i=0}{(1-P^D(x^i))}\prod_{i:\theta^i\ne0}{P^D(x^i)} \right] \\ & = \sum_{\theta \in \Theta} \left[ \frac{e^{-\bar{\lambda_c}}}{m!} \prod_{j: \nexists \theta^i=j} \lambda_c(z^j) \prod_{i:\theta^i=0}{(1-P^D(x^i))} \prod_{i: \theta^i\ne0}{P^D(x^i)g(z^{\theta^i}|x^i)} \right] \\ & = \sum_{\theta \in \Theta} \left[ \frac{e^{-\bar{\lambda_c}}}{m!} \prod_{j=1}^m \lambda_c(z^j) \prod_{i:\theta^i=0}{(1-P^D(x^i))} \prod_{i: \theta^i\ne0}{\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}} \right] \\ & \propto \sum_{\theta \in \Theta} \left[ \underbrace{\prod_{i:\theta^i=0}{(1-P^D(x^i))}}_{missed\;detections} \underbrace{\prod_{i: \theta^i\ne0}{\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}}}_{detections} \right] \end{aligned}

여기서 3번째 줄에서 4번째 줄로 넘어갈 때, 다음의 식이 곱해졌다.

1 = \frac{\prod_{j:\exist\theta^i=j}\lambda_c(z^j)}{\prod_{j:\exist\theta^i=j}\lambda_c(z^j)} = \frac{\prod_{i:\theta^i \ne 0}\lambda_c(z^{\theta^i})}{\prod_{i:\theta^i \ne 0}\lambda_c(z^{\theta^i})}

이때, 다수의 객체를 추적하므로 SOT보다 hypotheses가 굉장히 많아짐에 유의해야 하며, 다음과 같이 쓸 수 있다.

\begin{aligned} N_A(m,n) & = \sum^{min(m,n)}_{m^o=0} \begin{pmatrix} n\\ m^o \end{pmatrix} \begin{pmatrix} m\\ m^o \end{pmatrix} m^o! \\ & = \sum^{min(m,n)}_{m^o=0} \frac{m!n!}{m^o!(m-m^o)!(n-m^o)!} \end{aligned}

또한 posterior가 여러 분포의 혼합 분포라면, $N_0\prod_{t=1}^k N_A(m,n)$ 으로 쓸 수 있다.

3. Update and Prediction for n Objects

이제 다수의 객체에 대한 posterior density를 계산해보자.

\begin{aligned} p(X|Z) & \propto p(Z|X)p(X) \\ & \propto \sum_{\theta \in \Theta} \left[ \prod_{i':\theta^{i'}=0}{(1-P^D(x^{i'}))} \prod_{i: \theta^i\ne0}{\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}} \prod_{i''=1}^n p^{i''}(x^{i''}) \right] \\ & = \sum_{\theta \in \Theta} \left[ \prod_{i':\theta^{i'}=0}{(1-P^D(x^{i'}))p^{i'}(x^{i'})} \prod_{i: \theta^i\ne0}{\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}p^{i}(x^{i})} \right] \end{aligned}

앞 글에서 $p(x) \propto g(x)$ 일 때, $p(x) = \frac{g(x)}{\int g(x')dx'}$ 임을 살펴보았으며, 이를 적용해서 다음과 같이 쓸 수 있다.

\begin{aligned} In \; case & \; of \; \theta^i = 0, \\ &g(x^i) = (1-P^D(x^i))p^i(x^i) \;\; \rightarrow \;\; p ^{i,\theta^i}(x^i) = \frac{g(x^i)}{\tilde{w}^{\theta^i}}, \tilde{w}^{\theta^i} = \int g(x^i)dx^i \end{aligned}

\begin{aligned} In \; case & \; of \; \theta^i \ne 0, \\ &g(x^i) = \frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}p^i(x^i) \;\; \rightarrow \;\; p ^{i,\theta^i}(x^i) = \frac{g(x^i)}{\tilde{w}^{\theta^i}}, \tilde{w}^{\theta^i} = \int g(x^i)dx^i \end{aligned}

위 식을 사용하여 다음과 같이 posterior density를 표현할 수 있다.

\begin{aligned} p(X|Z) & \propto \sum_{\theta \in \Theta} \left[ \prod_{i':\theta^{i'}=0}{(1-P^D(x^{i'}))p^{i'}(x^{i'})} \prod_{i: \theta^i\ne0}{\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}p^{i}(x^{i})} \right] \\ & = \sum_{\theta \in \Theta} \prod_{i=1}^n \tilde{w}^{\theta^i} p^{i,\theta^i}(x^i) \end{aligned}

\tilde{w}^{\theta^i} = \begin{cases} \int (1-P^D(x^i))p^i(x^i) dx^i \;\;\;\;\;\; if \; \theta^i = 0 \\ \int{\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}p^i(x^i)} dx^i \;\;\;\;\;\;\; if \; \theta^i \ne 0 \end{cases}

p^{i,\theta^i}(x^i) = \begin{cases} \frac{1}{\tilde{w}^{\theta^i}}(1-P^D(x^i))p^i(x^i) \;\;\;\;\;\; if \; \theta^i = 0 \\ \frac{1}{\tilde{w}^{\theta^i}}\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}p^i(x^i) \;\;\;\;\;\;\; if \; \theta^i \ne 0 \end{cases}

이를 이용하여 posterior density를 normalize하면 다음과 같다.

\begin{aligned} p(X|Z) & \propto \sum_{\theta \in \Theta} \prod_{i=1}^n \tilde{w}^{\theta^i} p^{i,\theta^i}(x^i) = \sum_{\theta \in \Theta} \prod_{i'=1}^n \tilde{w}^{\theta^{i'}} \prod_{i=1}^n p^{i,\theta^i}(x^i) \\ & = \sum_{\theta \in \Theta} \tilde{w}^{\theta} \prod_{i=1}^n p^{i,\theta^i}(x^i) = \sum_{\theta \in \Theta} \tilde{w}^{\theta} p^{\theta}(X) \\ \; \end{aligned}

p(X|Z) = \sum_{\theta \in \Theta} w^\theta p^\theta(X)

w^\theta = \frac{\tilde{w}^{\theta}}{\sum_{\theta'} \tilde{w}^{\theta'}} = \frac{\prod_{i}\tilde{w}^{\theta^i}}{\sum_{\theta'}\prod_{i'}\tilde{w}^{\theta'^{i'}}}

다음의 figure 2에서 Gaussian prior를 사용하는 예시를 볼 수 있다.

Figure 2. Gaussian prior를 사용하는 예시

이제 다음과 같은 mixture prior를 가정하여 더 일반화된 식을 작성해보자.

p(X) = \sum_h Pr(h)p(X|h)w^h p^h(X) = \sum_h Pr(h)p(X|h)

위의 식을 사용하더라도 다음과 같이 posterior를 어떤 함수의 weigted sum으로 쓸 수 있다.

\begin{aligned} p(X|Z) & \propto p(Z|X)p(X) = \left[ \sum_{\theta \in \Theta } p(Z,\theta|X) \right]\left[ \sum_{h} w^h p^h(X) \right] \\ & = \sum_{h} \sum_{\theta \in \Theta} w^h p(Z,\theta|X) p^h(X) = \sum_{h} \sum_{\theta \in \Theta} w^h \tilde{w}^{\theta|h}\frac{p(Z,\theta|X) p^h(X)}{\tilde{w}^{\theta|h}} \\ & = \sum_{h} \sum_{\theta \in \Theta} \tilde{w}^{h,\theta}p^{h,\theta}(X) \end{aligned}

이때, $\tilde{w}^{\theta|h} = \int{p(Z,\theta|X)p^h(X)dX}=p(Z,\theta|h)$ 이다. 위 식을 normalize하여 다음과 같이 확률분포를 나타낼 수 있다.

p(X|Z) = \sum_{h} \sum_{\theta \in \Theta} w^{h,\theta}p^{h,\theta}(X) = \sum_{h} \sum_{\theta \in \Theta} Pr(h,\theta)p(X|h,\theta)

w^{h,\theta} = \frac{ \tilde{w}^{\theta|h} w^h }{\sum_{h} \sum_{\theta \in \Theta} \tilde{w}^{\theta|h} w^h}

여기에 time step k까지 추가하면 다음과 같이 쓸 수 있으며, 이러한 posterior를 통해 객체의 state에 대한 update를 수행할 수 있다.

p_{k|k}(X_k)=p_{X_k | Z_{1:k}}(X_k | Z_{1:k}) \propto \sum_{\theta_{1:k}} \tilde{w}^{\theta_{1:k}}_{k|k} p^{\theta_{1:k}}_{k|k} (X_k)

\tilde{w}^{\theta_{1:k}}_{k|k} = \prod_{i=1}^n \prod_{t=1}^n \tilde{w}^{\theta_{t}^i|\theta_{1:t-1}}

p^{\theta_{1:k}}_{k|k} (X_k) = \prod_{i=1}^n p^{i,\theta^i_{1:k}}_{k|k} (x^i_k)

이제 n개의 객체에 대한 prediction 과정을 살펴보자. Prediction을 위한 transition density는 다음과 같이 쓸 수 있다.

p_k(X_k|X_{k-1}) = p_k(x^1_k,x^2_k, \cdots, x^i_k, \cdots, x^n_k)

이때, 각 객체가 독립적으로 운동한다고 가정하면 다음과 같이 하나의 motion model을 사용하여 다음과 같이 간단하게 표현할 수 있다.

p_k(X_k|X_{k-1}) = \prod_{i=1}^n \pi_k(x^i_k|x^i_{k-1})

n개의 객체에 대한 Chapman-Kolmogorov prediction 식은 다음과 같다(위에서 사용된 notation처럼 $p_{k|k-1} (X_k)$ 가 $p_{X_k | Z_{1:k-1}}(X_k | Z_{1:k-1})$ 를 나타내는 notation임에 주의).

p_{k|k-1} (X_k) = \int p_k(X_k|X_{k-1})p_{k-1|k-1}(X_{k-1}) d X_{k-1}

Posterior $p_{k-1|k-1}(X_{k-1})$ 또한 각 객체에 대해 독립이라고 가정하면 다음과 같이 쓸 수 있다.

p_{k-1|k-1}(X_{k-1}) = \prod_{i=1}^n p^i_{k-1|k-1}(x^i_{k-1})

\begin{aligned} p_{k|k-1} (X_k) & = \int p_k(X_k|X_{k-1}) p_{k-1|k-1}(X_{k-1}) d X_{k-1} \\ & = \int \int \cdots \int \left[ \prod_{i=1}^n \pi_k(x^i_k|x^i_{k-1}) \right] \left[ \prod_{i'=1}^n p^{i'}_{k-1|k-1}(x^{i'}_{k-1}) \right] d x^1_{k-1} \cdots x^n_{k-1} \\ & = \prod_{i=1}^n \int \pi_k(x^i_k|x^i_{k-1}) p^{i}_{k-1|k-1}(x^{i}_{k-1}) d x^i_{k-1} = \prod_{i=1}^n p^i_{k|k-1} (x^i_k) \end{aligned}

Posterior $p_{k-1|k-1}(X_{k-1})$ 가 mixture density라면 다음과 같으며, weight가 유지됨을 알 수 있다.

p_{k-1|k-1}(X_{k-1}) = \sum_{h} w^h_{k-1|k-1} p_{k-1|k-1}(X_{k-1})

\begin{aligned} p_{k|k-1} (X_k) & = \int p_k(X_k|X_{k-1}) p_{k-1|k-1}(X_{k-1}) d X_{k-1} \\ & = \int p_k(X_k|X_{k-1}) \left[ \sum_{h} w^h_{k-1|k-1} p_{k-1|k-1}(X_{k-1}) \right] dX \\ & = \sum_{h} w^h_{k-1|k-1} \int p_k(X_k|X_{k-1}) p_{k-1|k-1}(X_{k-1}) dX = \sum_{h} w^h_{k-1|k-1} p^h_{k|k-1} (X_k) \end{aligned}

다만, 각 객체가 독립적으로 운동한다는 가정은 상황에 따라 틀린 가정이 될 수 있음에 유의하여야 한다.

Figure 3. Gaussian prior를 사용하는 예시 (동영상도 참고)

4. Data Association as an Optimization Problem

Mixture posterior의 업데이트 식 등에서 모든 data association에 대한 summation이 요구되는데 한정된 컴퓨팅 자원 상에서 이렇게 모든 data association에 대해 연산을 하는 것은 매우 힘들다. 따라서 우리는 근사를 통해 불필요한 연산을 줄이는 작업이 필요하며, 이를 해결하기 위한 대표적인 아이디어는 큰 weight $\tilde{w}^{\theta_k|h}$ 를 갖는 $\theta_k \in \tilde{\Theta}_k$ 를 원소로 하고, 전체 data association set보다 크기가 작은( $|\tilde{\Theta}_k| \ll |\Theta_k|$ ) subset $\tilde{\Theta}_k$ 을 찾는 것이다. 다만 이 과정에서 weight의 크기를 비교하기 위해 모든 $\theta_k$ 를 비교해서는 안된다.

이를 수행하기 위하여 data asscoation 문제를 최적화(optimization) 문제로 생각하여 풀게 된다. 비슷한 문제로 작업할당 문제가 있는데, 여러 면의 worker에게 각각의 작업을 할당하며, 이때 발생하는 비용이 최소화되는 할당 방법을 찾는 문제이다. 이 문제를 matrix로 표현하면 다음과 같이 cost matrix와 assignment matrix로 표현할 수 있다.

\begin{aligned} Cost \; & Matrix : \\ & L = \begin{pmatrix} 5 & 8 & 7\\ 8 & 12 & 7 \\ 4 & 8& 5 \end{pmatrix} \end{aligned}

\begin{aligned} Assignment \; & Matrix : \\ & A = \begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} \end{aligned}

여기서 cost matrix는 각 worker가 해당 작업을 수행했을 때 발생하는 비용을 포함하는 matrix이며, assignment matrix는 어떤 worker가 어떤 작업을 맡고 있는 지를 표현한다(worker $w^i$ 가 작업 $t^j$ 을 맡았을 때, $A^{i, j}=1$ , 아니라면, $A^{i, j}=0$ 이다).

위와 같이 matrix가 주어졌을 때, 발생하는 총 비용은 다음과 같이 구할 수 있다.

Cost = \sum_i \sum_j A^{i, j}L^{i, j} = tr(A^TL)

이제 data association을 위와 같은 형태로 적용해보자. 주어진 $h$ 에 대해서 optimal data association $\theta^* \in \Theta$ 는 다음과 같이 weight를 최대화 한다.

\tilde{w}^{\theta^* | h} \ge \tilde{w}^{\theta | h}, \forall \theta \in \Theta

따라서 optimal data association을 찾기 위한 optimization 문제는 다음과 같이 쓸 수 있다.

\theta^* = \underset{\theta \in \Theta}{argmax} \; \tilde{w}^{\theta | h} = \underset{\theta \in \Theta}{argmax} \; \prod_{i=1}^n \tilde{w}^{\theta^i | h}

여기에 단조 증가 함수인 log를 적용하여도 마찬가지로 maximization 문제로 유지된다.

\theta^* = \underset{\theta \in \Theta}{argmax} \; \log{\left( \prod_{i=1}^n \tilde{w}^{\theta^i | h} \right)} = \underset{\theta \in \Theta}{argmax} \; \sum_{i=1}^n \log (\tilde{w}^{\theta^i | h})

여기에 -1을 곱하여 minimization 문제로 치환한다.

\theta^* = \underset{\theta \in \Theta}{argmin} \; \sum_{i=1}^n -\log (\tilde{w}^{\theta^i | h})

이렇게 치환된 문제는 다음과 같이 비용을 최소화하는 opimization 문제와 같으며, 해당 최적화 문제의 해법을 적용할 수 있다.

A^* = \underset{A}{argmin} \; tr(A^TL)

Data association 문제의 assignment matrix는 $n \times (m+n)$ matrix로 표현할 수 있으며, 이는 환경에 존재하는 n개의 객체와 측정값이 포함하는 m개의 검출결과 및 n개의 미검출값 간의 할당을 표현한다. 예를 들어 $\theta^i = j$ 와 같이 i번째 객체가 j번째 측정값에 연관되어 있다면 $A^{i,j}=1$ 과 같이 표현하고, $\theta^i = 0$ 와 같이 i번째 객체가 미검출되었다면, $A^{i,m+i}=1$ 와 같이 표현한다(다른 element는 0). 전체적인 형태는 다음 그림과 같으며, 검출결과에 따른 $n \times m$ sub matrix와 미검출에 따른 $n \times n$ 대각 행렬로 이루어져 있다.

Figure 4. Data association 문제의 assignment matrix 예시

이제 cost matrix를 살펴보자. 위에서 전개한 식에 따르면 주어진 hypothesis h에 대해서 un-normalized association weight는 다음과 같다.

\tilde{w}^{\theta^i|h} = \begin{cases} \int (1-P^D(x^i))p^{i,h}(x^i) dx^i \;\;\;\;\;\; if \; \theta^i = 0 \\ \int{\frac{P^D(x^i)g(z^{\theta^i}|x^i)}{\lambda_c(z^{\theta^i})}p^{i,h}(x^i)} dx^i \;\;\;\;\;\;\; if \; \theta^i \ne 0 \end{cases}

이 식에 log를 적용하여 log-likelihood를 다음과 같이 구할 수 있다.
미검출일 때는

l^{i,0,h}=\log \left( \int (1-p^D(x^i))p^{i,h}(x^i)dx^i \right)

검출되었을 때, 즉 $x^i$ 가 $z^i$ 에 연관되었을 때는 다음과 같다.

l^{i,j,h}=\log \left( \int{\frac{P^D(x^i)g(z^{j}|x^i)}{\lambda_c(z^{j})}p^{i,h}(x^i)} dx^i \right)

Figure 5. Linear Gaussian일 때, log-likelihood 예시

이제 위와 같이 계산된 negative log-weight의 합을 최소화 해야하는데, 전체 cost는 다음과 같이 assignment matrix를 통해 표현될 수 있다.

\sum_{i=1}^n -\log (\tilde{w}^{\theta^i | h}) = \sum_{i=1}^n \sum_{j=1}^m A^{i,j} (-l^{i,j,h}) + \sum_{i'=1}^n A^{i',m+i'} (-l^{i,0,h})

이제 적당한 형태의 cost matrix $L$ 을 정의하면 다음과 같이 최적화 문제의 형태로 적을 수 있으며, 그 $L$ 의 형태는 다음 그림과 같은 예시를 들 수 있다. Assignment matrix와 마찬가지로 검출결과에 따른 $n \times m$ sub matrix와 미검출에 따른 $n \times n$ 대각 행렬로 이루어져 있고, $tr(A^TL^h)$ 가 negative log를 나타내는 식이므로 $\tilde{w}^{\theta | h} = exp(-tr(A^TL^h))$ 로 계산할 수 있다(주어진 data association $\theta$ 에 대한 weigth).

\sum_{i=1}^n -\log (\tilde{w}^{\theta^i | h}) = \sum_{i=1}^n \sum_{j=1}^{m+n} A^{i,j} L^{i,j,h} = tr(A^TL^h)

Figure 5. Cost matrix 예시

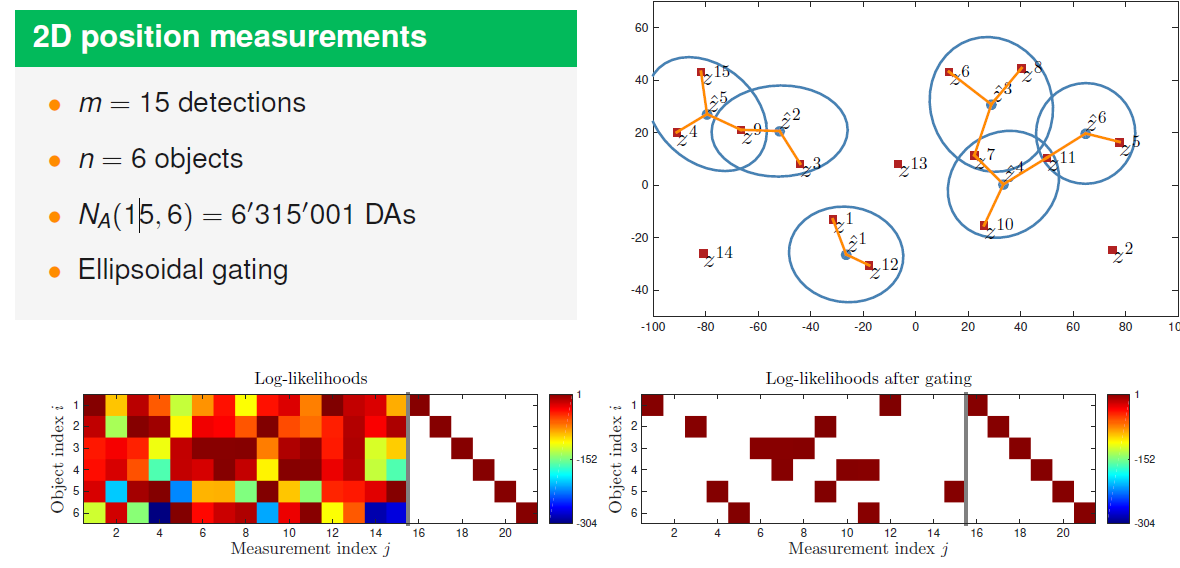
해결해야하는 전체적 최적화 문제는 다음과 같이 요약할 수 있고, 이러한 문제를 풀기위한 방법으로 best solution $A^*$ 를 찾는 Hungarian, Auction, Jonker-Volgenant-Castanon(JVC), M개의 best assignment를 찾고 cost가 증가하는 방향으로 rank를 매기는 Murty's, sub-opitimal solution을 찾지만 효율적인 연산이 가능한 Gibbs sampling 등의 방법이 있다.

\begin{aligned} & minimize \;\;\;\;\; tr(A^tL) \\ & subject \; to \;\;\;\;\; A^{i,j} \in \{0, 1\}, \;\;\;\;\;\;\;\;\;\;\;\;\; i,j \in \{1, \cdots, n\} \times \{1, \cdots, n+m\} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sum^{n+m}_{j=1} A^{i,j} = 1, \;\;\;\;\;\;\;\;\;\;\;\;\; i \in \{1, \cdots, n\} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sum^{n}_{j=1} A^{i,j} \in \{0,1\}, \;\;\;\;\;\;\; j \in \{1, \cdots, n+m\} \end{aligned}

또한 SOT gating을 통해 연산량을 줄일 수 있는 데 gating에서는 특정 distance 함수를 정의하고, 해당 distance가 일정 threshold 이상으로 증가하면 해당 association을 무시한다. 예를 들어 distance 함수는 다음과 같이 ellipsoidal gating distance를 정의할 수 있으며, 이는 figure 5의 log-likelihood에도 나타난다.

d_{i,j,h}^2 = (z^{j}_k - \hat{z}^{i,h}_{k|k-1})^T (S^{i,h}_{k})^{-1}(z^{j}_k - \hat{z}^{i,h}_{k|k-1})

해당 distance가 커지면 log-likelihood는 감소하고, threshold G 이상으로 증가하면 해당 association $l^{i,j,h}=-\infin$ 로 설정하여 무시한다.

Figure 6. Gating의 효과, 6,315,001개의 DA를 매우 많이 줄일 수 있다.

또한 뒤에서는 연산량을 줄이기 위한 여러 tracking algorithm을 소개한다.

고영민

이전 포스트