1. 문제

---

출처: 백준 2751번 수 정렬하기 2

2. 풀이

---

시간 복잡도가 $O(nlogn)$ 정렬 알고리즘을 활용해 보라고 문제에 설명이 되어있다.

예시로 나와 있는 병합 정렬과 힙 정렬 중 병합 정렬을 활용해 보았다.

병합 정렬 (Merge Sort)

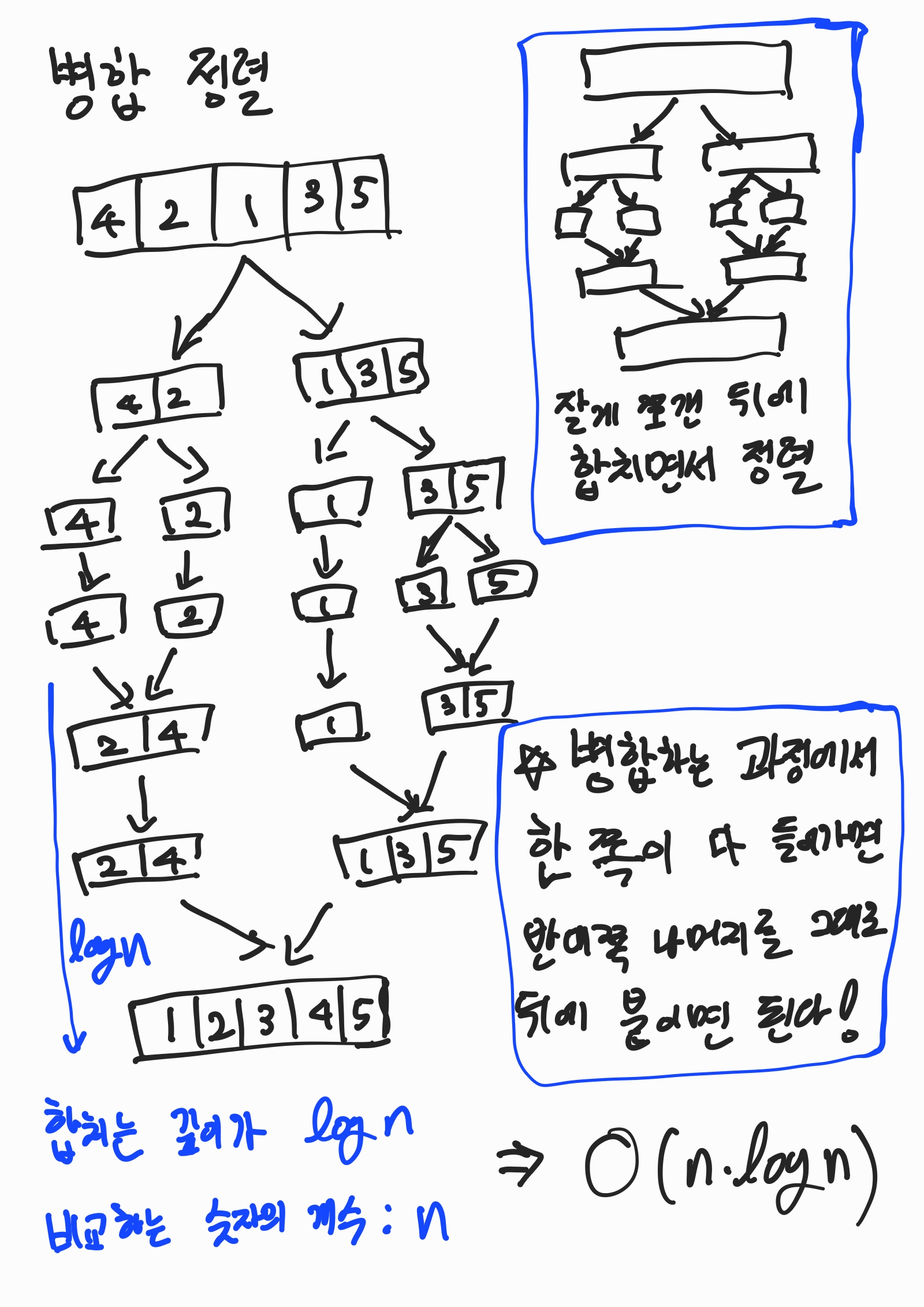
병합 정렬은 주어진 숫자 리스트를 1개 또는 0개로 쭉 쪼갠 이후에, 다시 합치는 과정에서 정렬을 하는 알고리즘이다.

앞뒤로 절반씩 쭉 리스트를 쪼개고, 합칠 때에는 작은 숫자를 새로운 리스트에 먼저 넣어주는 방식이다.
합쳐 가는 과정에서 비교를 하는 두 개의 리스트 중 한 쪽을 모두 새로운 새로운 리스트에 넣게 되면, 남은 것들은 이미 정렬이 되어 있으므로 새로운 리스트의 뒤에 그대로 붙여주기만 하면 된다.

합쳐 가는 과정의 깊이가 $log(n)$이고, 비교하는 숫자의 개수가 $n$이므로 시간 복잡도는 $O(nlogn)$이 된다.

시간 복잡도는 작은 편이지만, 새로운 리스트에 값을 집어넣는 형태로 합쳐나가기 때문에 메모리는 2배로 들게 된다는 단점이 있다.

3. 소스코드

---

import sys
input = sys.stdin.readline

N = int(input())
numbers = [int(input()) for _ in range(N)]

def merge_sort(arr):
    if len(arr) < 2:
        return arr
    mid = len(arr)//2
    low = merge_sort(arr[:mid])
    high = merge_sort(arr[mid:])

    # 비교해서 합치는 과정
    l,h = 0,0
    merge = []
    while l < len(low) and h < len(high):
        if low[l] < high[h]:
            merge.append(low[l])
            l += 1
        else:
            merge.append(high[h])
            h += 1
    
    # 남은 부분은 이미 정렬 되어 있으므로 단순하게 뒤에 붙여준다.
    merge += low[l:]
    merge += high[h:]
    return merge

result = merge_sort(numbers)
print(*result, sep="\n")

4. 그 외

---

대학교 수업에서 처음 해당 알고리즘을 들었을 때, 무슨 소리인가 했었다.
그래도 나이가 먹고 나니, 예전보다는 금방 이해하게 되는 듯하다.