백준 문제 풀이
1.[백준] 문제 풀이 기록을 시작하며
실질적 능력 향상을 위해 문제 풀이 기록을 시작하고자 한다.
2.[백준 1000번][Python/파이썬] A+B
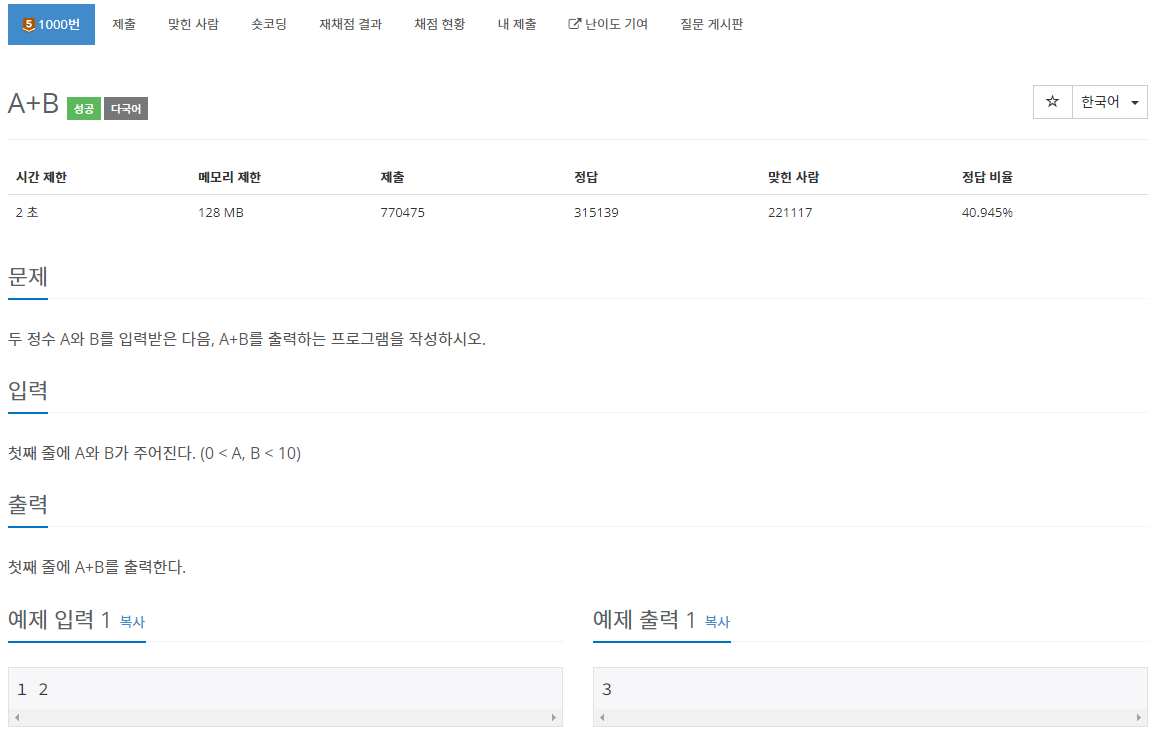
아주 단순한 문제임에도 풀이를 올리는 이유는, 앞으로 계속 활용하게 될 input 방법에 관해 정리해두고 싶었기 때문이다.
3.[백준 15552번][Python/파이썬] 빠른 A+B
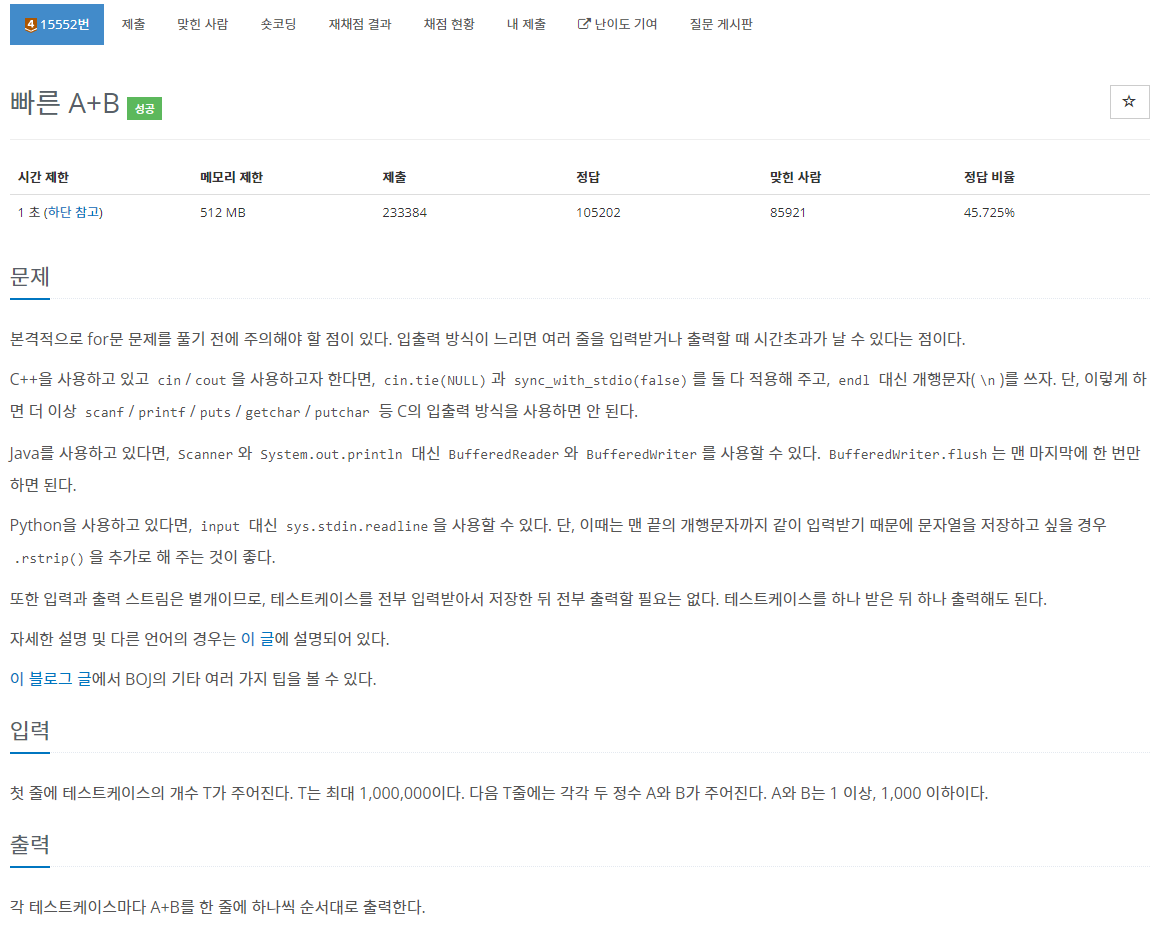
이번 문제는 앞으로 자주 사용하게 될 입력방법을 익힐 수 있는 문제였다.
4.[백준 10951번][Python/파이썬] A+B - 4
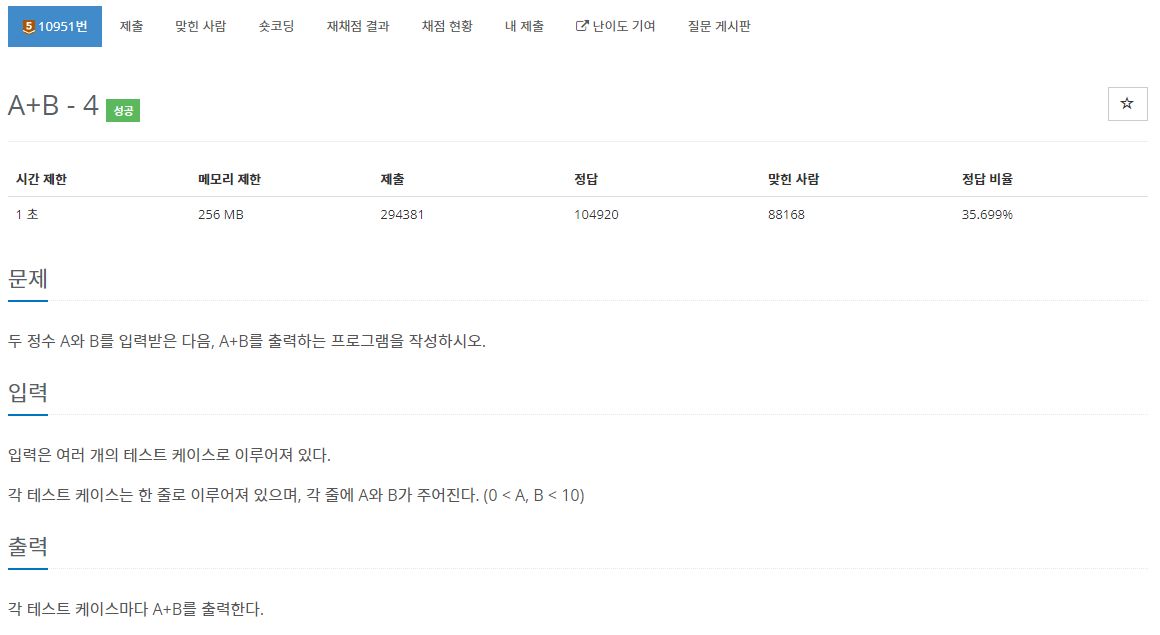
앞선 A+B 문제들과 다른 게 있는지 처음엔 알아채기 어려웠다. 따로 입력이 끝나는 순간을 알려주지 않기 때문에, 이 순간을 try, except를 활용해서 처리해 주는 것을 연습하는 문제이다.
5.[백준 5597번][Python/파이썬] 과제 안 내신 분...?
list의 pop과 index 기능을 활용하면 해당 문제를 굉장히 쉽게 풀 수 있다. 또는, list의 remove를 활용해도 가능하다.
6.[백준 3052번][Python/파이썬] 나머지
Python에서 중복된 요소를 다루는 데 굉장히 유용하게 사용할 수 있는 set을 다뤄볼 수 있는 문제이다.
7.[백준 4344번][Python/파이썬] 평균은 넘겠지
결과값을 출력할 때에, 소수점 세 자릿수까지 표현하는 법을 기록해두기 위하여 풀이를 적어둔다.
8.[백준 4673번][Python/파이썬] 셀프 넘버
어떤 방식으로 각 자릿수를 더해주는 것이 좋은지가 이 문제의 핵심이다. map과 문자열 성질을 적극 활용하면 된다.
9.[백준 1316번][Python/파이썬] 그룹 단어 체커
단어의 문자를 하나씩 체크해나가면서 다른 문자열에 저장해 나간다. 앞선 문자와 같은 문자를 체크할 때에는 그대로 저장하면 되지만, 다를 때 문제가 된다. 만약에 다르다고 판별된 문자가 이전에 나왔던 문자라면, 떨어져 나타난 문자가 있다
10.[백준 1712번][Python/파이썬] 손익분기점
가변 비용이 노트북 가격보다 크거나 같다면, 아무리 노트북을 많이 팔아도 고정 비용을 메꿀 수 없게 된다. 노트북 가격이 가변 비용이 큰 경우에, 팔아야 하는 노트북의 개수가 자연수로 딱 떨어지는지 아닌지를 확인해서 출력해 주면 된다.
11.[백준 2869번][Python/파이썬] 달팽이는 올라가고 싶다
달팽이가 정상에 올라가기 위해서는 전 날에 V-A만큼 이상 올라가 있으면 된다.
12.[백준 10250번][Python/파이썬] ACM 호텔
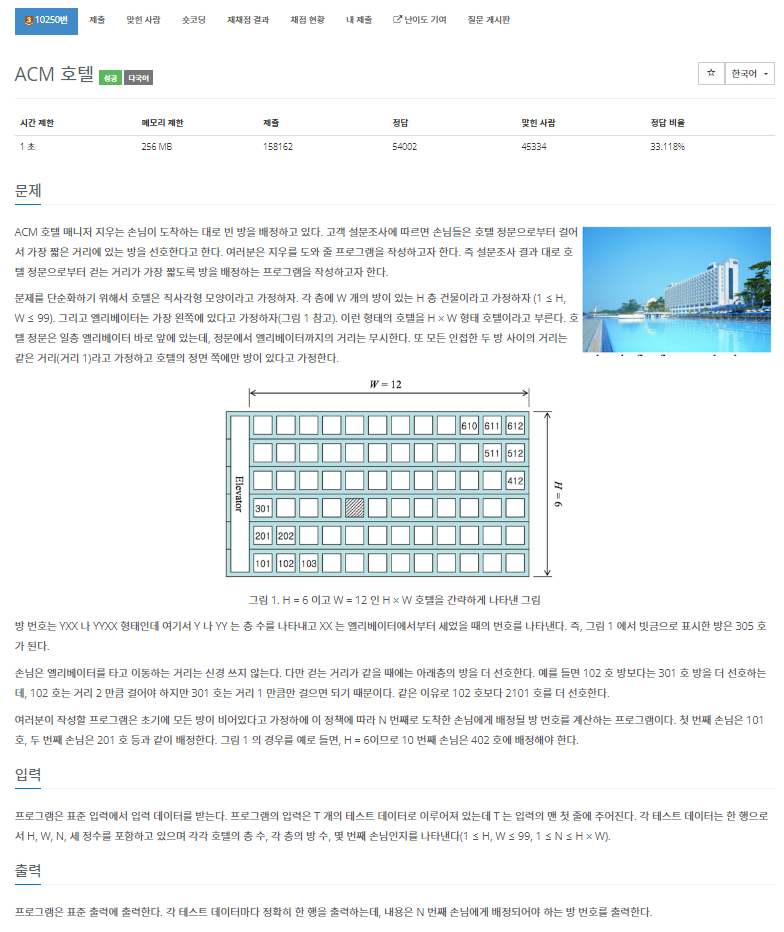
방문하는 손님 순서대로 그림의 왼쪽 아래부터 오른쪽 위로 방을 배정해 주면 되는 문제이다.
13.[백준 2839번][Python/파이썬] 설탕 배달
5킬로그램 봉지가 더 큰 단위기 때문에, 최대한 챙기는 것이 개수를 줄이는 데 도움이 된다.
14.[백준 1978번][Python/파이썬] 소수 찾기
해당 문제는 구해야 하는 소수의 범위가 1000이하로 작은 편이기 때문에, 에라토스테네스의 체를 사용하지 않아도 된다.
15.[백준 1929번][Python/파이썬] 소수 구하기
이전 문제들에서는 소수의 정의를 이용하여, 그때 그때 소수를 구해왔다. 그렇게 하면, 소수를 구해야 하는 소수 범위에 따라서 너무 많은 계산을 요구하게 될 수 있다. 이번에는 "에라토스테네스의 체"를 이용하자.
16.[백준 9020번][Python/파이썬] 골드바흐의 추측
제한에 적혀있는 범위까지 미리 소수를 구해둔다. 그다음, 작은 소수부터 주어진 숫자까지 가능한 골드바흐 파티션이 있는지 확인한다. 소수를 확인할 때에, 시간 초과가 되지 않도록 주의한다.
17.[백준 2563번][Python/파이썬] 색종이
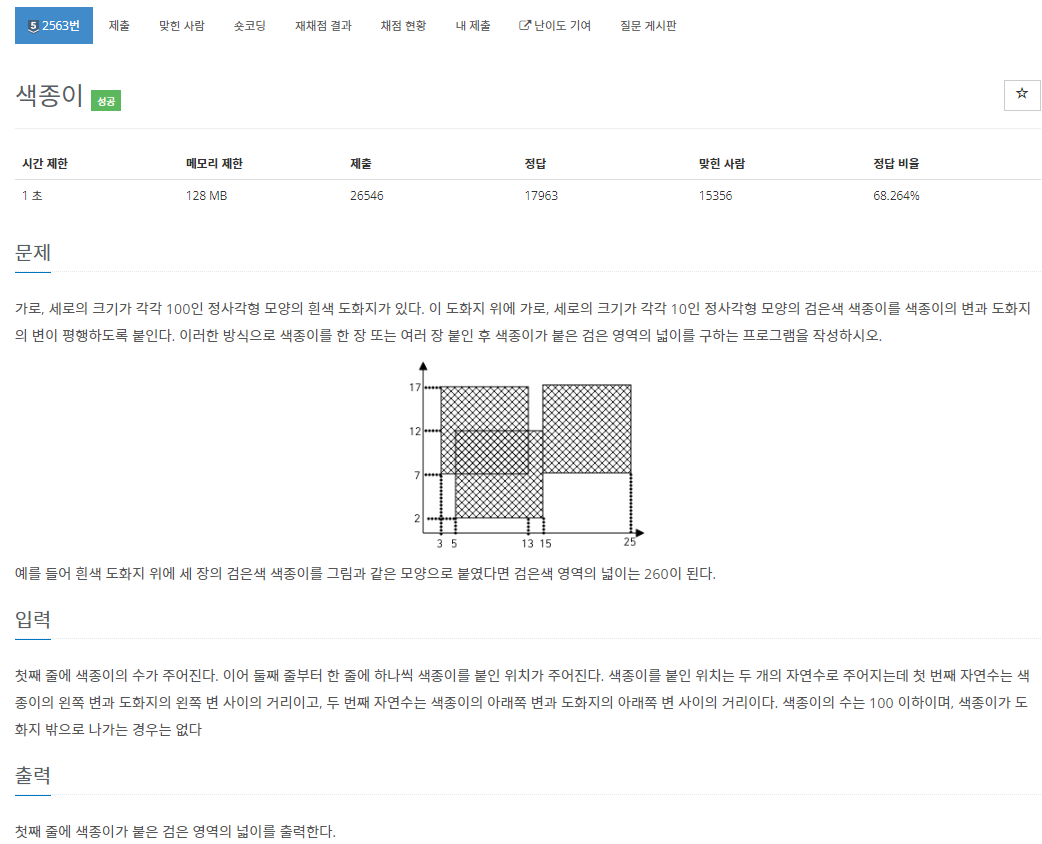
2차원 배열을 이용하여, 붙어있는 색종이의 위치를 표현하는 문제이다. 각 위치를 2차원 배열의 index로 활용하고, 색종이가 붙어있는 곳은 True로, 아닌 곳은 False로 표현하면 간단하게 문제를 풀 수 있다.
18.[백준 2750번][Python/파이썬] 수 정렬하기
시간 복잡도 O(n^2) 정렬 알고리즘. 삽입 정렬과 거품 정렬을 활용해 보았다.
19.[백준 2751번][Python/파이썬] 수 정렬하기 2
시간 복잡도 O(nlogn) 정렬 알고리즘. 병합 정렬을 활용해 보았다.
20.[백준 10989번][Python/파이썬] 수 정렬하기 3
문제에서 정렬할 수들의 최댓값이 10,000으로 주어졌고, 카운팅 정렬을 써보라고 하였으니 해당 알고리즘을 사용한다.
21.[백준 10870번][Python/파이썬] 피보나치 수 5
5피보나치 수를 구하는 점화식을 함수로 정의하고, 재귀를 이용하여 구현하면 된다. 뒤에 나올 다른 피보나치 수 문제를 위하여, 간단하기는 하지만 이것 또한 정리해 둔다.
22.[백준 2447번][Python/파이썬] 별 찍기 - 10
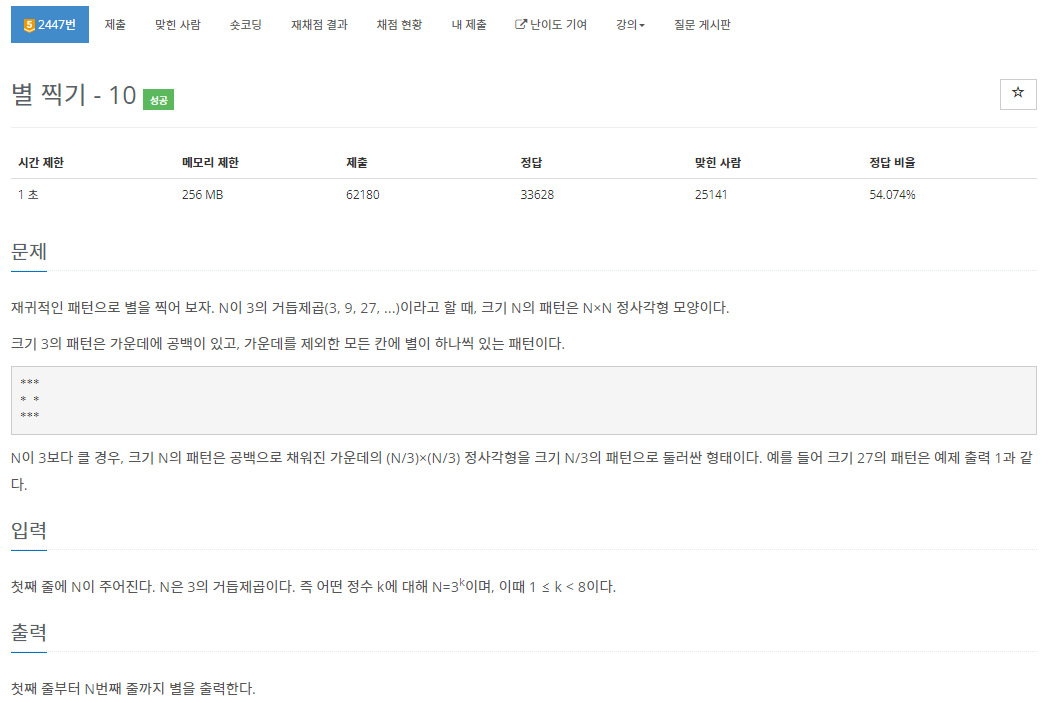
주어진 크기만큼 True로 구성된 N by N 리스트를 먼저 만든다. 그리고, 규칙에 따라서 비어있게 될 부분을 False로 바꿔주면 된다.
23.[백준 11729번][Python/파이썬] 하노이 탑 이동 순서
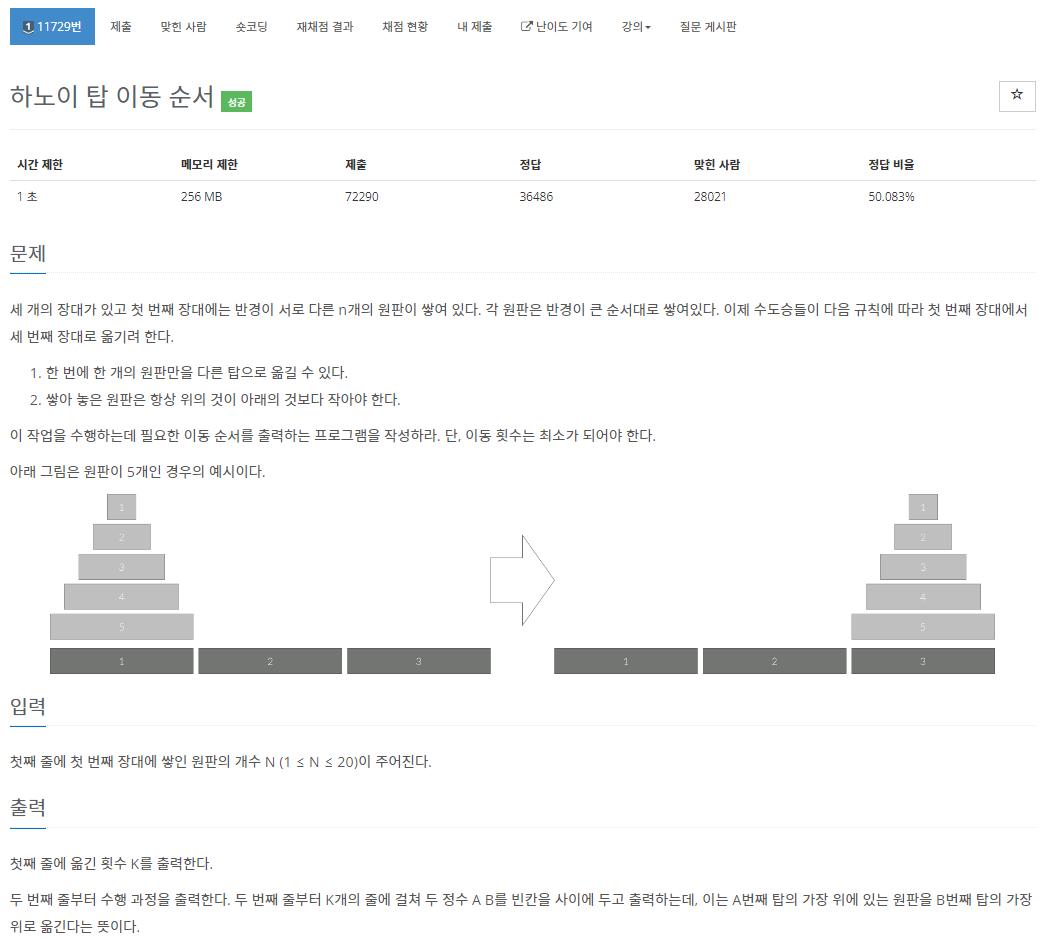
하노이 탑 이동 순서
24.[백준 2798번][Python/파이썬] 블랙잭
가능한 조합을 모두 구해서, 블랙잭 변형 규칙을 만족하는 것 중 최선의 값을 찾으면 된다.
25.[백준 7568번][Python/파이썬] 덩치
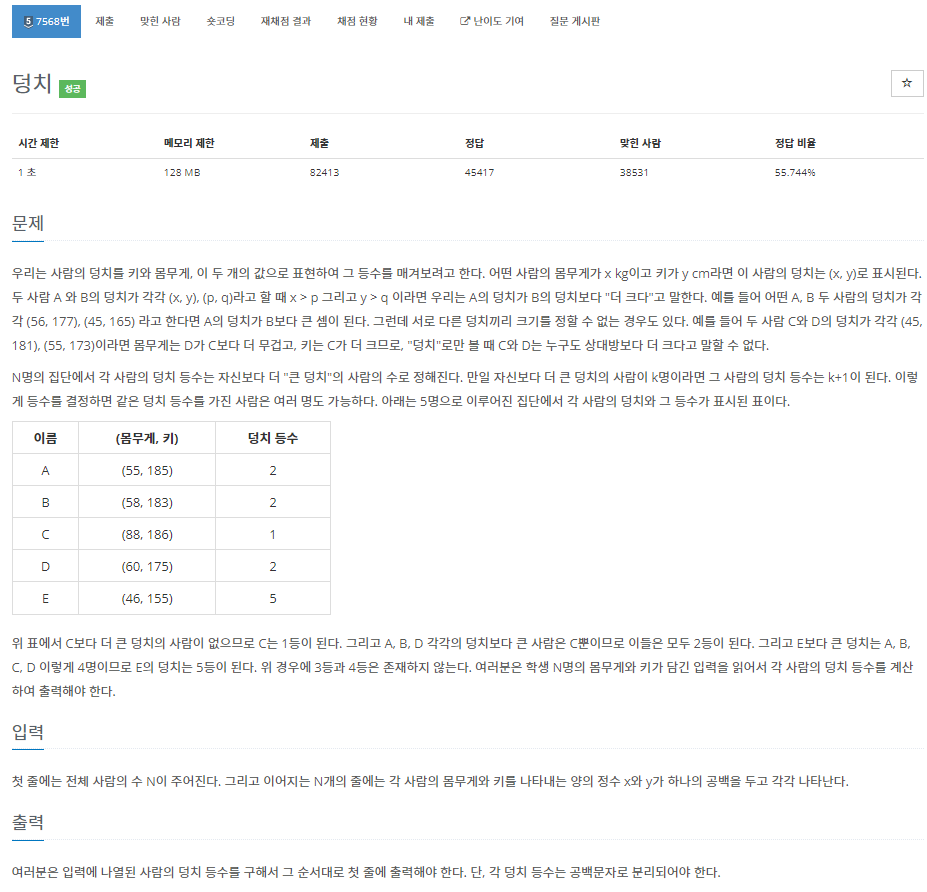
각 사람의 덩치를 다른 사람들과 모두 비교하여, 등수를 정해주면 되는 문제이다.
26.[백준 1018번][Python/파이썬] 체스판 다시 칠하기
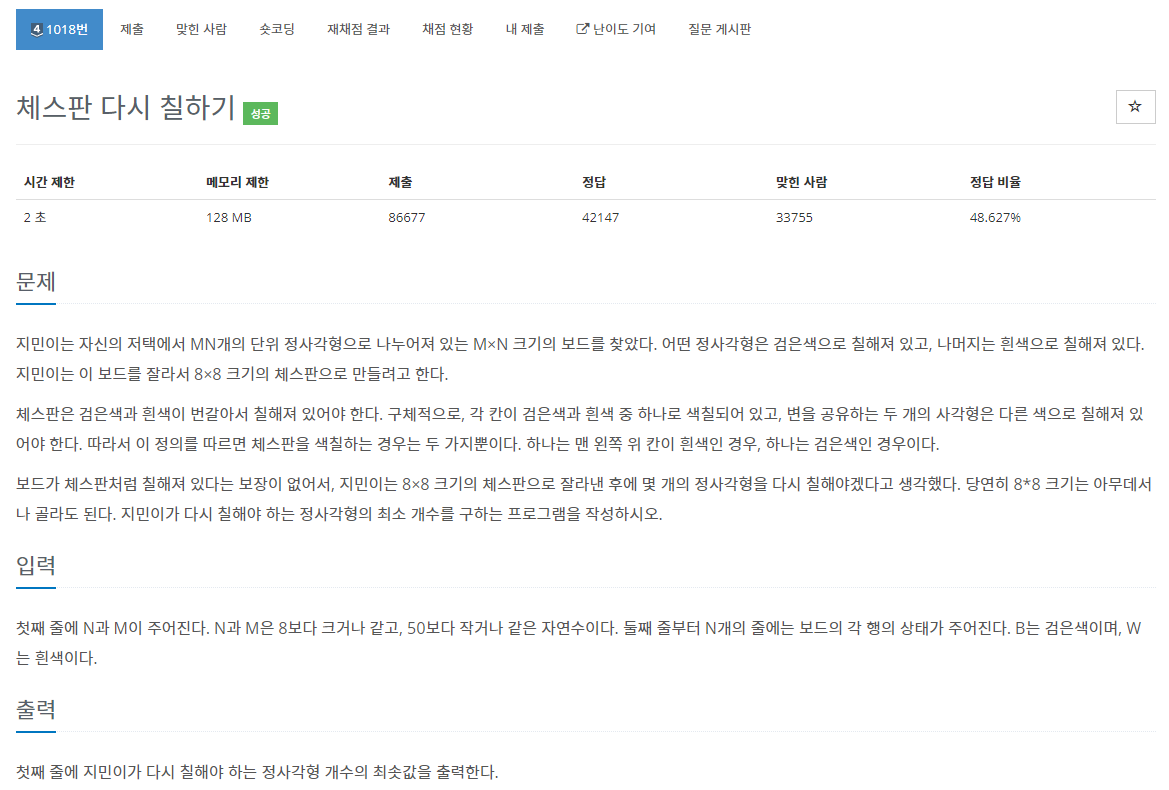
가능한 체스판의 경우는 BW가 반복되는 경우와 WB가 반복되는 경우가 있다. 주어진 보드를 쭉 잘라보면서, 위의 두 가지 경우와 얼마나 차이가 나는지 확인해 보면 된다.
27.[백준 10815번][Python/파이썬] 숫자 카드
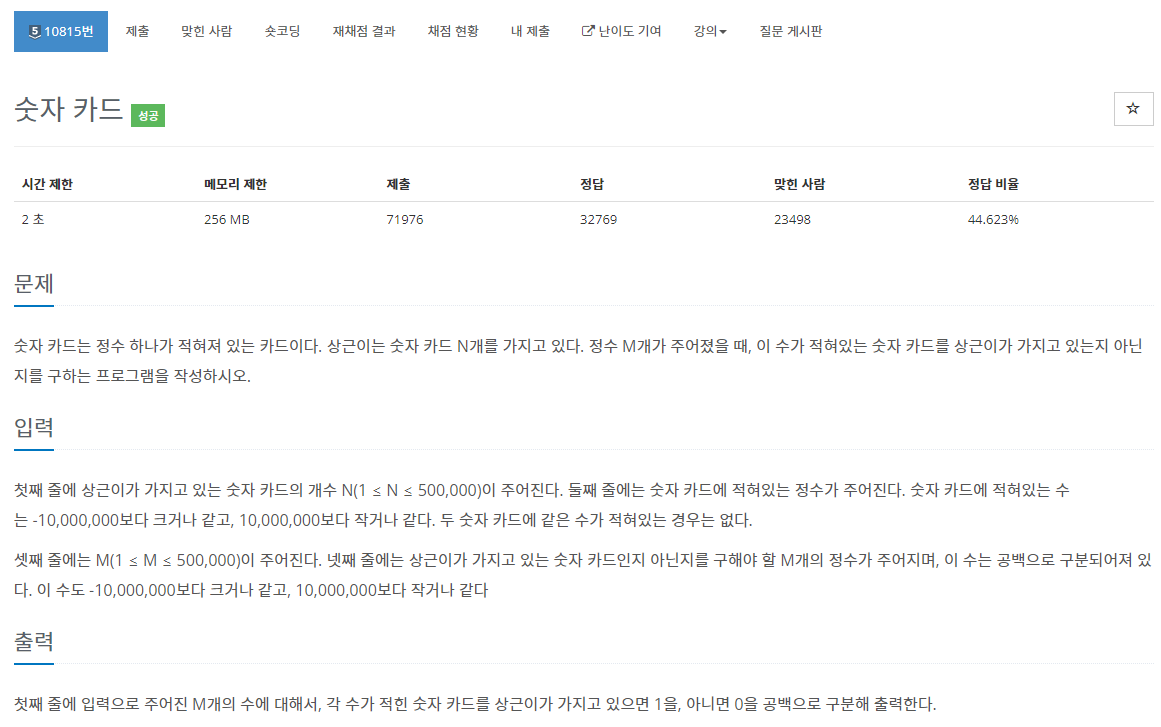
숫자 카드의 최대, 최솟값이 주어져 있으므로, 카운팅 정렬을 하는 것처럼 문제를 접근하면 된다.
28.[백준 14425번][Python/파이썬] 문자열 집합
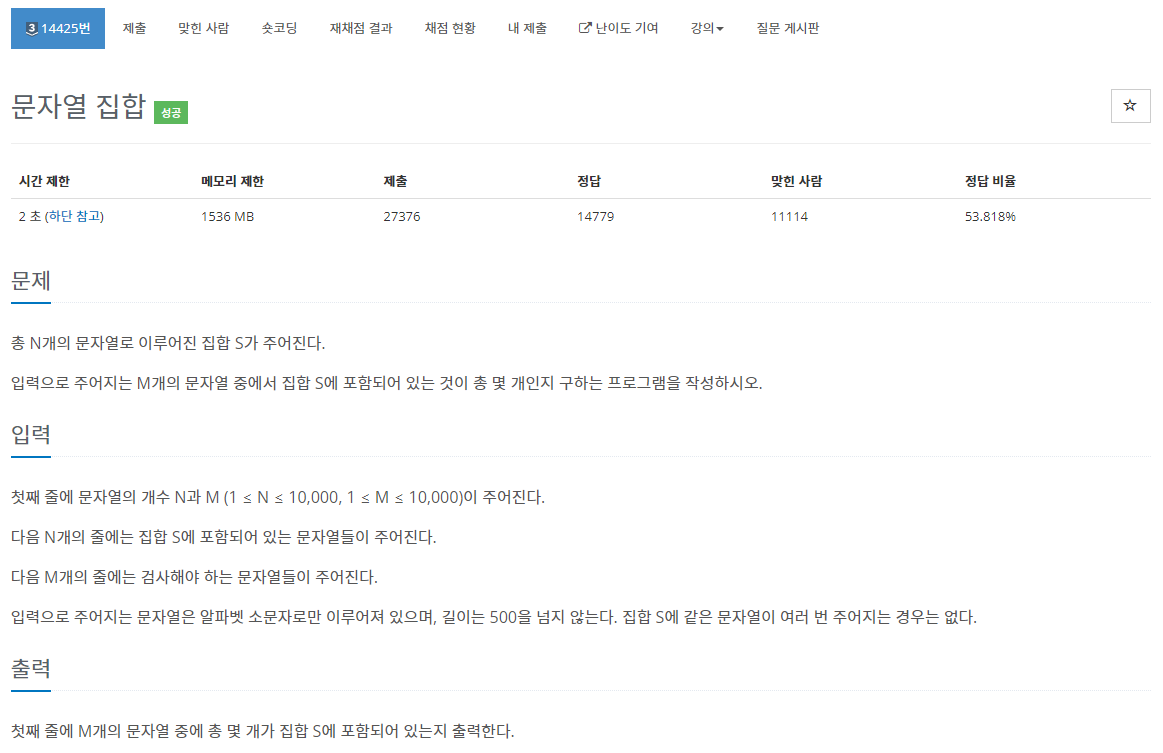
python에서 제공하는 set을 활용하면 해당 문제를 굉장히 쉽게 해결할 수 있다.
29.[백준 1620번][Python/파이썬] 나는야 포켓몬 마스터 이다솜
도감을 구성할 때 list를 사용하면, 검색하는데 시간이 너무 오래 걸리기 때문에 시간 초과가 발생하게 된다. 해시 테이블로 구성되는 dictionary를 사용해야 한다.
30.[백준 2477번][Python/파이썬] 참외밭
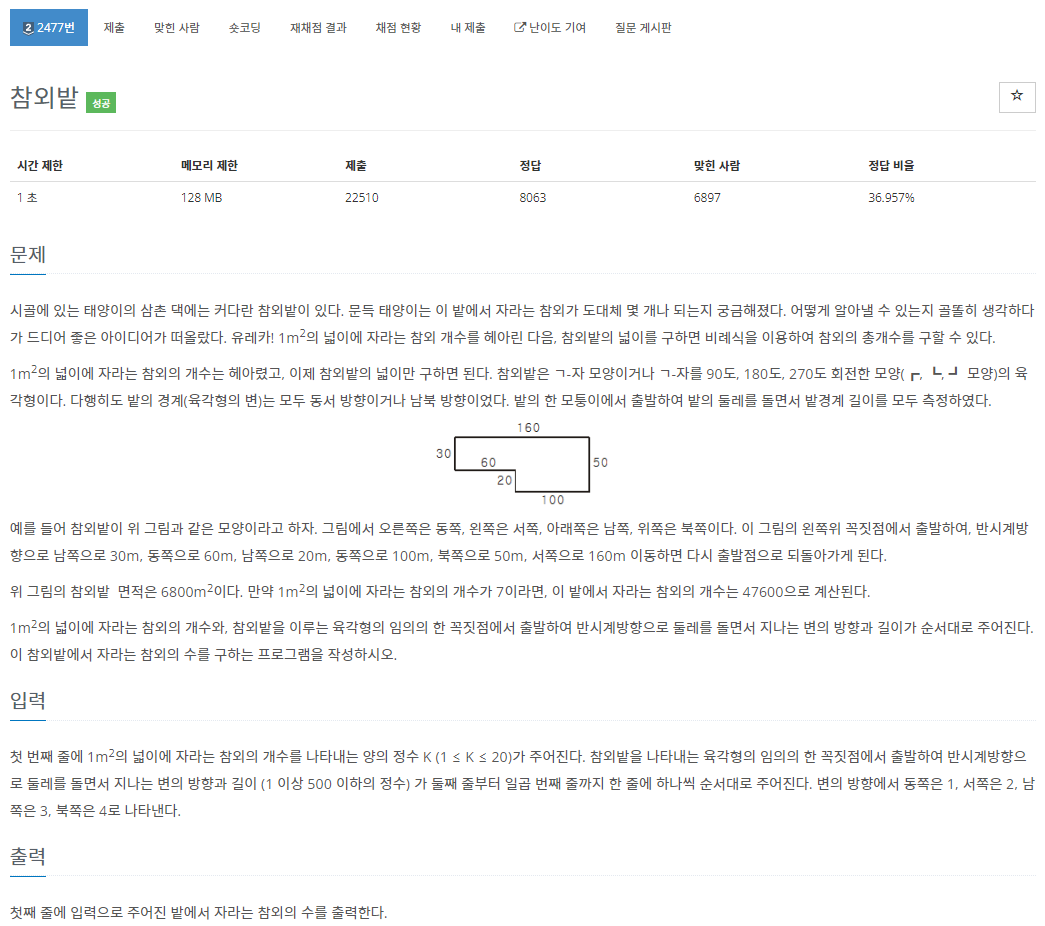
가로, 세로 가장 긴 변으로 그려지는 큰 사각형에서 밭에 포함되지 않는 작은 사각형을 빼주면 쉽게 밭의 넓이를 구할 수 있다.
31.[백준 1002번][Python/파이썬] 터렛
제 2 코사인 법칙 활용.
32.[백준 1004번][Python/파이썬] 어린 왕자
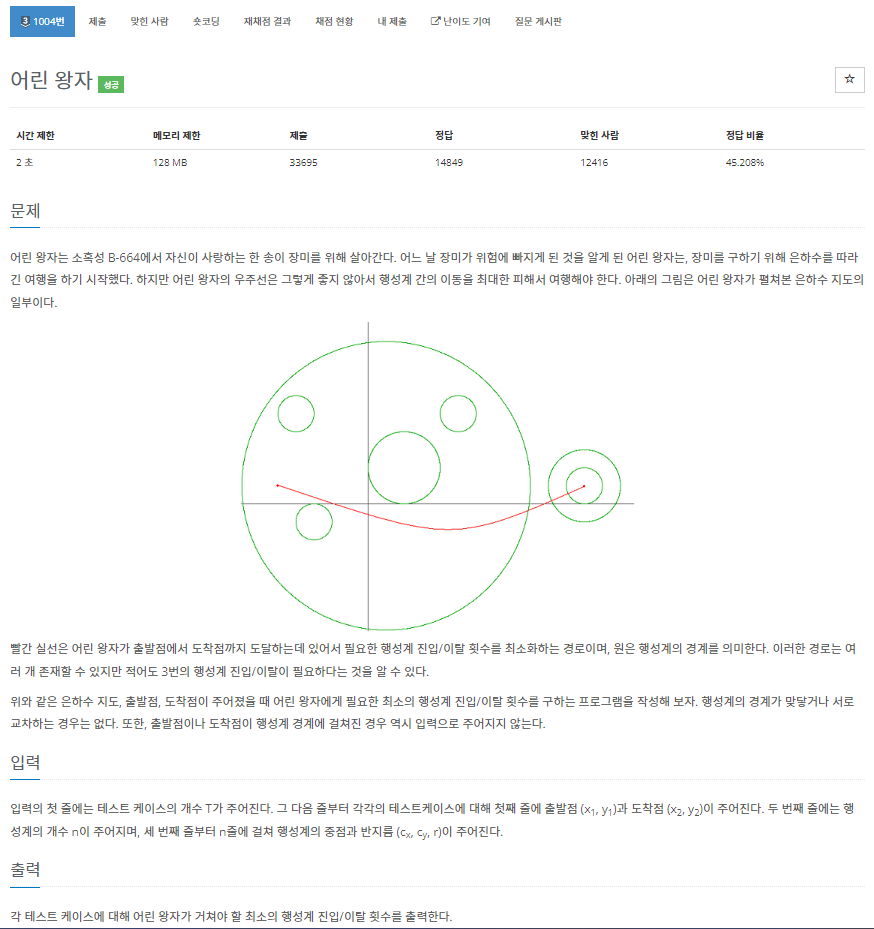
문제의 핵심은 출발점과 도착점이 얼마나 많은 행성계에 속해 있는지이다. 출발점이 속한 행성계들에서 이탈해서, 도착점이 속한 행성계들로 진입해야 하기 때문이다.
33.[백준 2609번][Python/파이썬] 최대공약수와 최소공배수
각 숫자의 약수들을 구하는 것에서부터 시작한다. 약수들을 오름차순으로 정렬했을 때 양 끝의 약수들끼리 곱하면 원래의 숫자가 나온다.
34.[백준 2981번][Python/파이썬] 검문
숫자들이 너무 크기 때문에, 그대로 일일이 계산한다면 시간 초과가 발생할 수밖에 없다. 따라서, 유클리드 호제법을 적극 활용해야 한다.
35.[백준 9375번][Python/파이썬] 패션왕 신해빈
입력으로 주어지는 의상들을 종류별로 분류하고, 알몸이 아닌 조합을 구하면 되는 문제이다. dictionary를 이용해서 분류하면 의상 종류를 검색하는 데 시간을 줄일 수 있다.
36.[백준 2004번][Python/파이썬] 조합 0의 개수
끝자리 0의 개수의 의미는 결국 10이 몇 번 곱해졌는 지로 생각할 수 있다. 10은 2와 5가 몇 번 곱해지를 구해서, 더 적게 곱해진 숫자만큼 10이 곱해진 것임을 알 수 있다.
37.[백준 15649번][Python/파이썬] N과 M (1)
결국 순열을 뽑으라는 문제여서, 처음에는 모듈을 쓰는 것인가 했었다. 다른 분들의 풀이를 참고하니, 대부분 DFS (Depth-First Search)를 쓰고 있었다. 드디어, 말로만 들어왔던 DFS를 쓰는 문제에 접어들었다.
38.[백준 9663번][Python/파이썬] N-Queen
퀸을 서로 공격할 수 없게 체스판에 둘려면, 2가지 조건을 만족해야 한다. 같은 열 값과 행 값을 가지는 퀸이 없을 것, 서로의 대각선 위치에 놓여있는 퀸들이 없을 것.
39.[백준 2580번][Python/파이썬] 스도쿠

스도쿠의 규칙은 각 행과 열에 1~9까지 숫자가 하나씩만 들어가고, 작은 박스에도 1~9까지의 숫자가 하나씩만 들어가는 것이다.
40.[백준 14888번][Python/파이썬] 연산자 끼워넣기
다행히도, 곱하기와 나누기의 연산 우선순위가 없기 때문에 문제를 단순하게 접근할 수 있다. 숫자를 하나씩 뽑아서, 남아있는 연산자 중 하나를 이용해 계산해 나가는 DFS를 구성하면 된다.
41.[백준 14889번][Python/파이썬] 스타트와 링크
가능한 팀 조합을 뽑고, 각 조합에 따른 점수 계산을 하고 최솟값을 찾는 순으로 풀이를 할 수 있다.
42.[백준 24416번][Python/파이썬] 알고리즘 수업 - 피보나치 수 1
동적 계획법(Dynamic Programming)은 반복되는 값을 잘 저장해두었다가 사용하는 memoization이 핵심이다.
43.[백준 9184번][Python/파이썬] 신나는 함수 실행
문제에 적혀 있는 재귀 함수를 함수로 구현하고, 속도 향상을 위해 동적 계획법(DP)을 섞어 주면 된다.
44.[백준 1904번][Python/파이썬] 01타일
n번 째에 가능한 숫자들은 (n-1)번 째 숫자들의 뒤에 1을 붙이는 것과 (n-2)번 째 숫자들의 뒤에 00을 붙이는 것으로 찾을 수 있다.
45.[백준 1912번][Python/파이썬] 연속합
문제 풀이의 핵심은 "연속"합이라는 데에 있다. 현재 숫자를 포함해서 쭉 숫자를 앞에서부터 더해온 값과 현재 숫자 하나만을 비교했을 때, 현재 숫자가 크다면 앞에서 더해온 값은 의미가 없다고 볼 수 있다.
46.[백준 1149번][Python/파이썬] RGB거리
집을 색칠하는 데 있어서, 다른 것은 고려하지 않아도 되고 앞뒷 집의 색깔들과만 다르면 된다.
47.[백준 2579번][Python/파이썬] 계단 오르기

계단을 오를 때, 지금 있는 위치에 오기 위해서는 두 가지의 경로가 있다. 2칸 전에서 2칸을 한 번에 오기. 3칸 전에서 2칸을 한 번에 옮겨 1칸 전으로 이동하고, 마저 1칸을 이동해 지금 칸으로 오기.
48.[백준 10844번][Python/파이썬] 쉬운 계단 수
계단수는 끝자리 숫자가 무엇이냐에 따라서 이전 계단수들의 개수를 활용해서 구하면 된다.
49.[백준 11053번][Python/파이썬] 가장 긴 증가하는 부분 수열
이 문제의 경우에는 어떤 수열인지는 구할 필요가 없고, 길이만 즉 포함된 숫자의 개수만 구하면 된다.
50.[백준 2156번][Python/파이썬] 포도주 시식
연속으로 3잔을 마실 수는 없기 때문에 포도주를 마시는 방법은 총 3가지로 분류할 수 있다. 지금 잔과 이전 잔을 마신다. 지금 잔만 마신다. 지금 잔을 마시지 않는다. 문제를 DP 방식으로 접근한다.
51.[백준 11054번][Python/파이썬] 가장 긴 바이토닉 부분 수열
이 문제는 수가 커지다가 작아지는 형태의 부분 수열을 구하는 것을 다루고 있다.
52.[백준 2565번][Python/파이썬] 전깃줄
증가하는 부분 수열을 이용하여 접근하면 되는 문제이다.
53.[백준 9251번][Python/파이썬] LCS
주어진 문자열을 쪼개서 끝자리를 하나식 비교해나가는 과정으로 DP 표를 만들고 풀이할 수 있다.
54.[백준 12865번][Python/파이썬] 평범한 배낭
2차원 DP 표를 만들어서 풀이하면 된다. 집어넣는 물건의 개수와 최대 가방 무게를 이용하여 2차원 DP 리스트를 만든다.
55.[백준 11659번][Python/파이썬] 구간 합 구하기 4
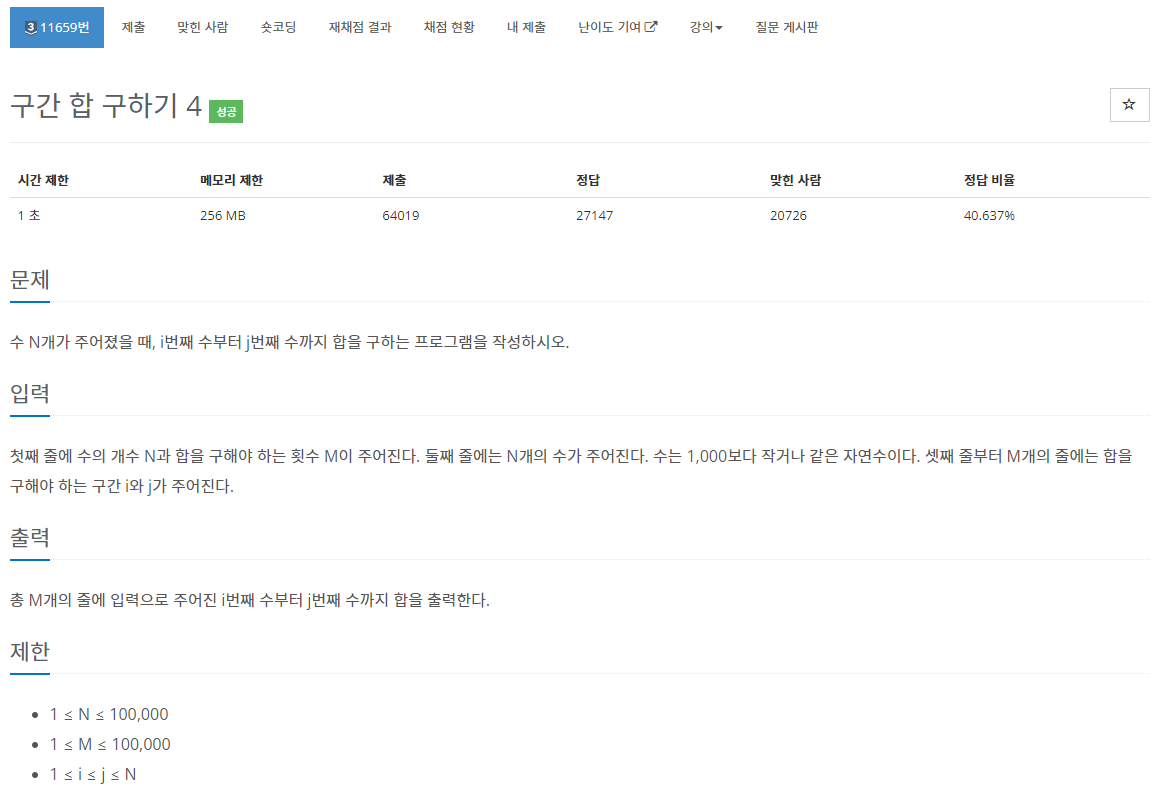
DP 접근 방식을 이용하여 선택한 숫자까지의 합을 쭉 더한 리스트를 생성한다. 주어진 i 번째 수부터 j 번째 수까지의 합을 구하고 싶다면, j 번째 DP 리스트에서 i 번째 DP 리스트를 빼주면 된다.
56.[백준 2559번][Python/파이썬] 수열
DP를 활용한 수열
57.[백준 16139번][Python/파이썬] 인간-컴퓨터 상호작용
알파벳의 아스키코드와 DP를 이용하는 문제이다.
58.[백준 10986번][Python/파이썬] 나머지 합
모듈러 연산은 더하기, 빼기를 하기 전에 미리 해도 유지되는 장점이 있다. 이 성질과 DP 접근 방식을 이용해 보자.
59.[백준 25682번][Python/파이썬] 체스판 다시 칠하기 2
이번 문제는 체스판의 크기가 커졌기 때문에, DP 방식으로 접근해야 한다.
60.[백준 1931번][Python/파이썬] 회의실 배정
최대한 많은 회의를 잡기 위해서는, 회의 시간이 짧은 것들을 최대한 집어넣으면 된다.
61.[백준 5430번][Python/파이썬] AC
풀이의 핵심은 뒤집는 함수를 직접 수행하기 보다는 간접적으로 결과를 뽑는데 있다.
62.[백준 1654번][Python/파이썬] 랜선 자르기
각 랜선을 정해진 크기로 잘랐을 때 몇 개가 나오는지 탐색해나가면 되는 문제이다. 이 때, 하나씩 올려가며 찾는 것은 시간이 n만큼 들기 때문에 절반씩 찾아가는 이분 탐색을 사용한다.
63.[백준 11286번][Python/파이썬] 절댓값 힙
절댓값을 이용해 최소힙 구조를 만들고, 같이 집어넣은 원래 값을 출력하는 방식으로 구현.