목적
ResNet 을 이해하고 Pytorch로 구현할 수 있다.
Architecture
-
Network architecture

-
Residual Block (Figure 5)
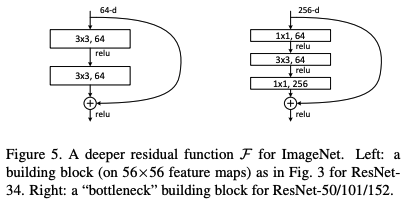
특징
-
등장배경
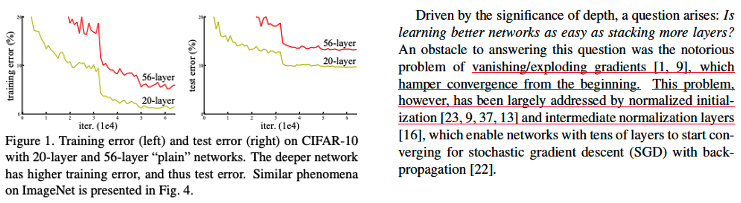
- Layer를 깊게 쌓았지만 얕게 쌓은 network 보다 더 성능이 좋지 않았음. -> underfitting
- 이론상 깊은 모델의 표현력은 얕은 모델의 표현력을 포함하면서 그 이상의 표현력을 가짐. 근데 왜 이런 현상이 일어났을까?
- 이 현상의 원인은 Gradient vanishing/exploding가 아님. 논문에서 언급한 것 처럼 만약 Gradient vanishing/exploding 문제가 있다면 학습 초기부터 일어나기 때문에 아예 모델의 loss가 어느 지점으로 수렴되지 않았어야 함. gradient 는 weight initialization, Batchnormalization, ReLU의 기법으로 충분히 크다.
- 즉 ,weight update가 잘 되지 않아서 생기는 문제가 아닌 다른 문제이다.
-> degradation - 이 논문에서는 skip connection (shortcut-connection)을 제안하여 이 문제를 해결하였음.
- 이 현상이 왜 일어났는지는 당시 ResNet 논문에서는 밝혀내지 못했지만 이후에 나온 2017년 12월에 출간된 Visualizing the Loss Landscape of Neural Nets 논문에 의하면 아래 그림처럼 skip connection 없이 layer를 깊게 쌓으면 loss 모양이 이상해졌기 때문임이 알려짐.
-> local minimum으로 빠지기 매우 쉬운 loss 형태.
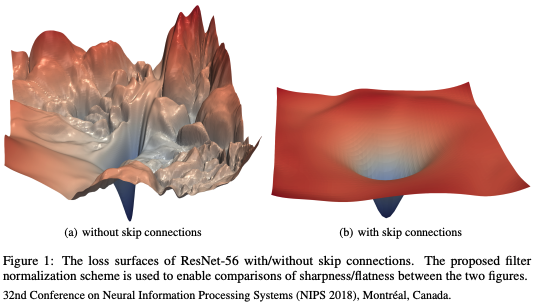
-
Residual learning: Building block
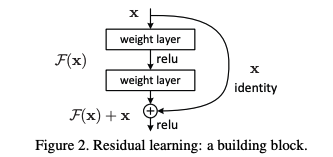
- 우리가 input으로 를 받아서 만들고 싶은 이상적인 결과가 라고 해보자.
- 가 기존의 일반적인 layer (=F(x)) 를 통과한다고 했을 때를 식으로 표현하면
-> 이다. - 가 skip-connection이 있는 layer (=F(x))를 통과한다고 했을 때를 식으로 표현하면
-> 이다. - 딱 이 차이 뿐인데 층을 깊게 쌓으면 skip-connection이 있는 쪽이 학습이 잘 된다. 왜 그럴까?
- 로 를 만들고 싶다고 가정해본다면,
- 일반 layer라면 weight matrix는 identity matrix가 되어야 함.
() - skip-connection 있는 layer라면 weight matrix는 zero matrix가 되어야 함.
(()
- 일반 layer라면 weight matrix는 identity matrix가 되어야 함.
- weight는 0 근처로 초기화 되므로 skip-connection이 더 를 만들기 쉬울 것임. (weight가 대각선 방향으로 1, 나머지는 0인 identity matrix로 되는 것 보다 zero matrix가 되는 것이 더 쉽다.)
- 근데 왜 일까?
-> 왜 만들고 싶은 이상적인 결과가 input이였던 x랑 비슷한가?
는 전체 network가 아닌 단지 몇 개의 layer로 이루어진 stacked layers가 뱉어내는 이상적인 결과이다. 즉, 입력과 출력이 크게 바뀌지 않을 것임. ()
-> 예시

- 즉, 입력과 출력의 차이 () 만 학습한다고 해서 ResNet이라는 이름이 붙음.
-> 입출력의 차이만 학습하면 되니깐 학습이 쉽다! - 일반적인 순서는 다음과 같다.
-> conv - BN - ReLU - conv - BN - (+ ) - ReLU
-
Bottleneck

- 50 layer 이상 부터는 오른쪽 구조 사용.
-> 1 x 1 conv를 사용해 모델 크기가 너무 커지지 않게 함.
-> 왼쪽의 block으로 50층을 쌓으면 파라미터 수 너무 많아짐.
-> 256 - 64 - 64 - 256: 채널 수를 줄였다 키우는 것을 볼 수 있음. (bottleneck)
- 50 layer 이상 부터는 오른쪽 구조 사용.
-
VGGNet과 구조 비교
- 이미지 size 줄일 때는 conv에 stride 2를 사용해서 줄임.
-> pooling은 처음의 max pool과 끝의 avg pool 만 사용함. - 실선은 identity skip-connection, 점선은 projection skip-connection을 나타냄.
-> projection skip-connection: 1x1 conv, stride = 2로 사이즈와 채널 수를 조절하여 skip-connection 연산이 가능하도록 맞춰줌.
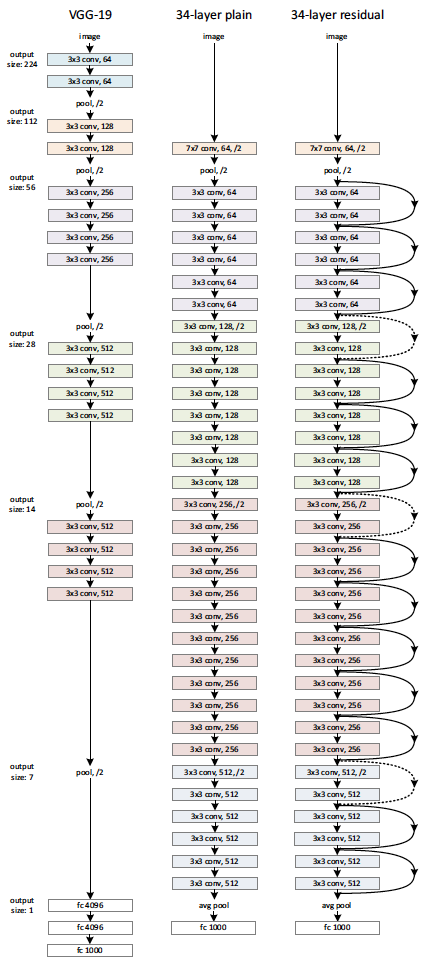
- 이미지 size 줄일 때는 conv에 stride 2를 사용해서 줄임.
Code
환경
- python 3.8.16
- pytorch 2.1.0
- torchinfo 1.8.0
구현
import torch
from torch import nn
from torchinfo import summaryclass BasicBlock(nn.Module):
expansion = 1
def __init__(self, in_channels, inner_channels, stride = 1, projection = None):
super().__init__()
self.residual = nn.Sequential(
nn.Conv2d(in_channels, inner_channels, 3, stride = stride, padding = 1, bias = False),
nn.BatchNorm2d(inner_channels),
nn.ReLU(),
nn.Conv2d(inner_channels, inner_channels * self.expansion, 3, padding = 1, bias = False),
nn.BatchNorm2d(inner_channels * self.expansion),
)
self.projection = projection
self.relu = nn.ReLU()
def forward(self, x):
residual = self.residual(x)
if self.projection is not None:
skip_connection = self.projection(x)
else:
skip_connection = x
out = self.relu(residual + skip_connection)
return out
class Bottleneck(nn.Module):
expansion = 4
def __init__(self, in_channels, inner_channels, stride = 1, projection = None):
super().__init__()
self.residual = nn.Sequential(
nn.Conv2d(in_channels, inner_channels, 1, stride = stride, bias = False),
nn.BatchNorm2d(inner_channels),
nn.ReLU(),
nn.Conv2d(inner_channels, inner_channels, 3, padding = 1, bias = False),
nn.BatchNorm2d(inner_channels),
nn.ReLU(),
nn.Conv2d(inner_channels, inner_channels * self.expansion, 1, bias = False),
nn.BatchNorm2d(inner_channels * self.expansion),
)
self.projection = projection
self.relu = nn.ReLU()
def forward(self, x):
residual = self.residual(x)
if self.projection is not None:
skip_connection = self.projection(x)
else:
skip_connection = x
out = self.relu(residual + skip_connection)
return out
class ResNet(nn.Module):
def __init__(self, block, num_block_list, n_classes = 1000):
super().__init__()
assert len(num_block_list) == 4
self.conv1 = nn.Sequential(
nn.Conv2d(3, 64, kernel_size = 7, stride = 2, padding = 3, bias = False),
nn.BatchNorm2d(64),
nn.ReLU(),
)
self.maxpool = nn.MaxPool2d(3, stride = 2, padding = 1)
self.in_channels = 64
self.stage1 = self.make_stage(block, 64, num_block_list[0], stride = 1)
self.stage2 = self.make_stage(block, 128, num_block_list[1], stride = 2)
self.stage3 = self.make_stage(block, 256, num_block_list[2], stride = 2)
self.stage4 = self.make_stage(block, 512, num_block_list[3], stride = 2)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(512 * block.expansion, n_classes)
def make_stage(self, block, inner_channels, num_blocks, stride = 1):
if stride != 1 or self.in_channels != inner_channels * block.expansion:
projection = nn.Sequential(
nn.Conv2d(self.in_channels, inner_channels * block.expansion, 1, stride = stride, bias = False),
nn.BatchNorm2d(inner_channels * block.expansion),
)
else:
projection = None
layers = []
for idx in range(num_blocks):
if idx == 0:
layers.append(block(self.in_channels, inner_channels, stride, projection))
self.in_channels = inner_channels * block.expansion
else:
layers.append(block(self.in_channels, inner_channels))
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.maxpool(x)
x = self.stage1(x)
x = self.stage2(x)
x = self.stage3(x)
x = self.stage4(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.fc(x)
return xdef resnet18(**kwargs):
return ResNet(BasicBlock, [2, 2, 2, 2], **kwargs)
def resnet34(**kwargs):
return ResNet(BasicBlock, [3, 4, 6, 3], **kwargs)
def resnet50(**kwargs):
return ResNet(Bottleneck, [3, 4, 6, 3], **kwargs)
def resnet101(**kwargs):
return ResNet(Bottleneck, [3, 4, 23, 3], **kwargs)
def resnet152(**kwargs):
return ResNet(Bottleneck, [3, 8, 36, 3], **kwargs)model = resnet50()
summary(model, input_size=(2,3,224,224), device='cpu')#### OUTPUT ####
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
ResNet [2, 1000] --
├─Sequential: 1-1 [2, 64, 112, 112] --
│ └─Conv2d: 2-1 [2, 64, 112, 112] 9,408
│ └─BatchNorm2d: 2-2 [2, 64, 112, 112] 128
│ └─ReLU: 2-3 [2, 64, 112, 112] --
├─MaxPool2d: 1-2 [2, 64, 56, 56] --
├─Sequential: 1-3 [2, 256, 56, 56] --
│ └─Bottleneck: 2-4 [2, 256, 56, 56] --
│ │ └─Sequential: 3-1 [2, 256, 56, 56] 58,112
│ │ └─Sequential: 3-2 [2, 256, 56, 56] 16,896
│ │ └─ReLU: 3-3 [2, 256, 56, 56] --
│ └─Bottleneck: 2-5 [2, 256, 56, 56] --
│ │ └─Sequential: 3-4 [2, 256, 56, 56] 70,400
│ │ └─ReLU: 3-5 [2, 256, 56, 56] --
│ └─Bottleneck: 2-6 [2, 256, 56, 56] --
│ │ └─Sequential: 3-6 [2, 256, 56, 56] 70,400
│ │ └─ReLU: 3-7 [2, 256, 56, 56] --
├─Sequential: 1-4 [2, 512, 28, 28] --
│ └─Bottleneck: 2-7 [2, 512, 28, 28] --
│ │ └─Sequential: 3-8 [2, 512, 28, 28] 247,296
│ │ └─Sequential: 3-9 [2, 512, 28, 28] 132,096
│ │ └─ReLU: 3-10 [2, 512, 28, 28] --
│ └─Bottleneck: 2-8 [2, 512, 28, 28] --
│ │ └─Sequential: 3-11 [2, 512, 28, 28] 280,064
│ │ └─ReLU: 3-12 [2, 512, 28, 28] --
│ └─Bottleneck: 2-9 [2, 512, 28, 28] --
│ │ └─Sequential: 3-13 [2, 512, 28, 28] 280,064
│ │ └─ReLU: 3-14 [2, 512, 28, 28] --
│ └─Bottleneck: 2-10 [2, 512, 28, 28] --
│ │ └─Sequential: 3-15 [2, 512, 28, 28] 280,064
│ │ └─ReLU: 3-16 [2, 512, 28, 28] --
├─Sequential: 1-5 [2, 1024, 14, 14] --
│ └─Bottleneck: 2-11 [2, 1024, 14, 14] --
│ │ └─Sequential: 3-17 [2, 1024, 14, 14] 986,112
│ │ └─Sequential: 3-18 [2, 1024, 14, 14] 526,336
│ │ └─ReLU: 3-19 [2, 1024, 14, 14] --
│ └─Bottleneck: 2-12 [2, 1024, 14, 14] --
│ │ └─Sequential: 3-20 [2, 1024, 14, 14] 1,117,184
│ │ └─ReLU: 3-21 [2, 1024, 14, 14] --
│ └─Bottleneck: 2-13 [2, 1024, 14, 14] --
│ │ └─Sequential: 3-22 [2, 1024, 14, 14] 1,117,184
│ │ └─ReLU: 3-23 [2, 1024, 14, 14] --
│ └─Bottleneck: 2-14 [2, 1024, 14, 14] --
│ │ └─Sequential: 3-24 [2, 1024, 14, 14] 1,117,184
│ │ └─ReLU: 3-25 [2, 1024, 14, 14] --
│ └─Bottleneck: 2-15 [2, 1024, 14, 14] --
│ │ └─Sequential: 3-26 [2, 1024, 14, 14] 1,117,184
│ │ └─ReLU: 3-27 [2, 1024, 14, 14] --
│ └─Bottleneck: 2-16 [2, 1024, 14, 14] --
│ │ └─Sequential: 3-28 [2, 1024, 14, 14] 1,117,184
│ │ └─ReLU: 3-29 [2, 1024, 14, 14] --
├─Sequential: 1-6 [2, 2048, 7, 7] --
│ └─Bottleneck: 2-17 [2, 2048, 7, 7] --
│ │ └─Sequential: 3-30 [2, 2048, 7, 7] 3,938,304
│ │ └─Sequential: 3-31 [2, 2048, 7, 7] 2,101,248
│ │ └─ReLU: 3-32 [2, 2048, 7, 7] --
│ └─Bottleneck: 2-18 [2, 2048, 7, 7] --
│ │ └─Sequential: 3-33 [2, 2048, 7, 7] 4,462,592
│ │ └─ReLU: 3-34 [2, 2048, 7, 7] --
│ └─Bottleneck: 2-19 [2, 2048, 7, 7] --
│ │ └─Sequential: 3-35 [2, 2048, 7, 7] 4,462,592
│ │ └─ReLU: 3-36 [2, 2048, 7, 7] --
├─AdaptiveAvgPool2d: 1-7 [2, 2048, 1, 1] --
├─Linear: 1-8 [2, 1000] 2,049,000
==========================================================================================
Total params: 25,557,032
Trainable params: 25,557,032
Non-trainable params: 0
Total mult-adds (G): 7.72
==========================================================================================
Input size (MB): 1.20
Forward/backward pass size (MB): 338.80
Params size (MB): 102.23
Estimated Total Size (MB): 442.24
==========================================================================================
와 굉장히 좋은 글이네요.
Visualizing the Loss Landscape of Neural Nets논문도 흥미로워서 재밌는거 같아요.
'Residual Networks Behave Like Ensembles of Relatively Shallow Networks'도 재밌게 읽었었는데, 이것도 추천드립니다!