정보이론 - Entropy, Cross-Entropy, KL-Divergence, Mutual information

Entropy

정보이론에서의 엔트로피는 정보를 표현하는데 필요한 최소 평균 자원량이다.

• 정보를 표현하는 단위는 bits로써 0 또는 1을 사용해 표현할 수 있다.
• 어떤 정보를 표현하는데 있어 bits가 길수록 더 많은 자원을 사용한 것
• 엔트로피는 정보를 표현하는데 있어 최소의 bits 길이로 표현한 것이다.

정보는 랜덤하므로 확률값을 갖는다. 이 확률 값을 기반으로 엔트로피를 정의할 수 있다. 엔트로피 입장에서 확률이 클수록 짧게, 확률이 작을수록 길게 코딩하는 것이 유리할 것이다.

• 예를 들어, 연인간의 톡에서 "하트"가 나올 확률이 "욕설"이 나올 확률보다 더 높을 것임을 생각할 수 있다. 이 때 "하트"와 "욕설"을 bits로 인코딩할 때 엔트로피 입장에서는 최소 자원을 이용해서 정보를 표현해야 하기 때문에 나올 확률이 높은 "하트"를 짧게 인코딩하고, "욕설"은 길게 인코딩해야 한다는 뜻이다.
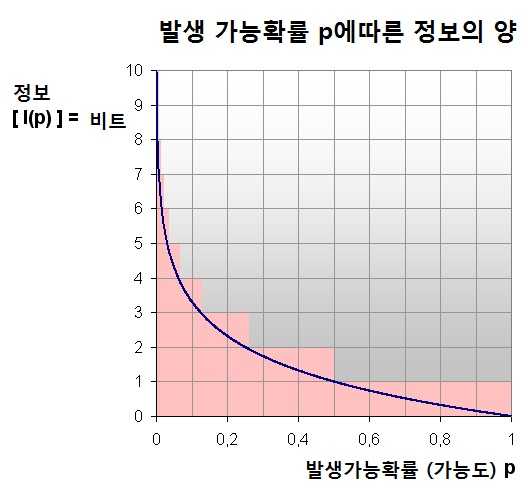  그림출처: 위키백과 (정보 엔트로피)
  $\\$
  이를 그래프로 나타내면 위와 같은 $-\log_a{p}$ 함수 이다.
  정보이론에서는 bits (0 또는 1)로 표현하므로 $a=2$ 이다.

이제 엔트로피 식을 유도해보자.

• 위 로그함수는 각 문자의 확률의 함수이므로 $-\log_2 p_i$로 표현할 수 있다.

• 엔트로피는 최소 "평균" "자원량" 이다.

  • 문자의 확률은 $p_i$이고, 이때 최소길이는 $-\log_2p_i$이다.
    이 둘을 곱하면 문자의 최소 자원량이 된다. $\rightarrow -p_i\log_2p_i$
  • 정보는 여러 문자들로 구성되어 있으므로 각 문자들의 최소 자원량을 합하여 기댓값으로 표현할 수 있다.
    $\\$

  $E_n=-\displaystyle\sum_i p_i \log_2p_i$

각 정보의 확률이 Uniform 할 때 Entropy가 최대가 된다.

• 효율적으로 인코딩 하기 위해서는 확률이 각 정보마다 달라야 할 것이기 때문이다.

연속형 확률변수일 때의 엔트로피는 $\displaystyle-\int p(x)\cdot\ln p(x) dx$ 으로 표현할 수 있다.

Cross-entropy

실제 확률 분포인 $P$를 모르는 상태에서 우리가 생각했을 때 (모델링 했을 때) 최선이라고 생각한 $Q$ 분포를 이용해 entropy를 구한 것.

식은 아래와 같다.
$\\$
$CE_n = -\displaystyle\sum_i p_i\log_2 q_i$
$\\$
우리가 생각한 최소길이는 $-\log_2 q_i$ 이지만 실제로는 확률분포 $P$를 따르므로
$q_i \cdot -\log_2 q_i$가 아닌 $p_i \cdot -\log_2 q_i$ 로 표현한다.
$\\$

KL-divergence

이상적인 분포인 $P$ 분포와 $Q$ 분포의 차이를 계산한 것이다.
(확률변수 $P$를 따르는데 $Q$를 따른다고 했을 때 얼마나 비효율적인가? 를 계산한 것)
식은 아래와 같다. (여기부터 log의 밑은 생략하겠다.)
$\\$
$KL \space divergence = CE_n-E_n = -\displaystyle\sum_ip_i \log q_i + \displaystyle\sum_ip_i \log p_i$
$\\$

Mutual information

두 변수 사이의 상호 의존성을 측정한 것
(하나의 확률변수가 다른 확률변수에 얼마나 영향을 미치는지 알 수 있다.)
식은 아래와 같다.

$mutual \space information = \displaystyle\sum_i\sum_jp(x_i, y_i)\log\frac{p(x_i, y_i)}{p(x_i)\cdot p(y_i)}$

$\\$
이 식이 무슨 뜻일까
먼저 KD-divergence 식을 예쁘게 정리해보자.
$\\$
$KL \space divergence = \displaystyle\sum_ip_i\cdot \log\frac{p_i}{q_i}$
$\\$
이 식은 "실제로는 확률분포 $P$를 따르는데 확률분포 $Q$를 따른다고 했을 때 얼마나 비효율적인가?" 를 계산하기 위한 식이다. Mutual information도 똑같이 해석할 수 있다.
$\\$
$\rightarrow$ 원래는 $p(x_i, y_i)$를 따르는데 (독립이 아닌데), $p(x_i)\cdot p(y_i)$를 따른다고 했을 때 (독립이라고 했을 때), 얼마나 비효율적인인가? 로 해석하면 된다.
$\rightarrow$ Mutual information 값이 클수록 둘 사이는 상호의존적이다. (독립이 아니다.)

• 참고
  $p(x_i, y_i)$와 $p(x_i)\cdot p(y_i)$는 무슨관계인가?
  $\rightarrow$ $p(x_i, y_i)$에서 $x, y$가 독립일 때, $p(x_i)\cdot p(y_i)$로 표현할 수 있다.
  $\\$
  만약 독립이라면, $p(x_i|y_i) = p(x_i) \rightarrow \displaystyle\frac{p(x_i, y_i)}{p(y_i)}=p(x_i)$ 이므로,
  이를 전개하면 $p(x_i, y_i) = p(x_i)\cdot p(y_i)$
  $\\$

Reference

• https://www.youtube.com/watch?v=z1k8HVU4Mxc