
자료구조와 알고리즘
자료구조와 알고리즘이란?
자료구조 + 알고리즘 = 프로그램
자료구조
메모리를 효율적으로 사용하며 빠르고 안정적으로 데이터를 처리하는 것이 궁극적인 목표로, 상황에 따라 유용하게 사용될 수 있도록 특정 구조를 이루고 있습니다.
- 상황에 맞는 올바른 자료구조를 고를 수 있는 능력이 필요하다!
- Stack, Queue, Graph, Tree, ...
알고리즘
특정 문제를 효율적이고 빠르게 해결하는 것이 궁극적인 목표로, 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것을 의미합니다.
- Binary Search (이진 탐색), Shortest Path (최단거리 탐색), ...
자료구조와 알고리즘이 중요한 이유?
실무에서 중요하게 생각하는 요인
- 기초 코딩 능력
- 전문 분야 지식
- 기본 CS 지식
자료구조와 알고리즘 공부를 통해 기초 코딩 능력을 기를 수 있습니다.
문제 해결 능력
- 논리적 사고
- 전산화 능력 (컴퓨팅 사고)
ex. 현실에 존재하는 영화 예매를 어떻게 컴퓨터로 옮길지?
1) 영화를 검색한다.(Trie)ㅎ
2) 고객이 영화표 예매 줄을 선다. (Queue)
3) 고객이 좌석을 선택한다. (HashTable) - 엣지 케이스 탐색 (예외 사항을 찾는 능력)
자료구조의 종류
자료구조는 일차원인 컴퓨터 메모리를 현실에 대응되도록 구조를 만든 것!
선형구조와 비선형구조에 대해 배울 것입니다.
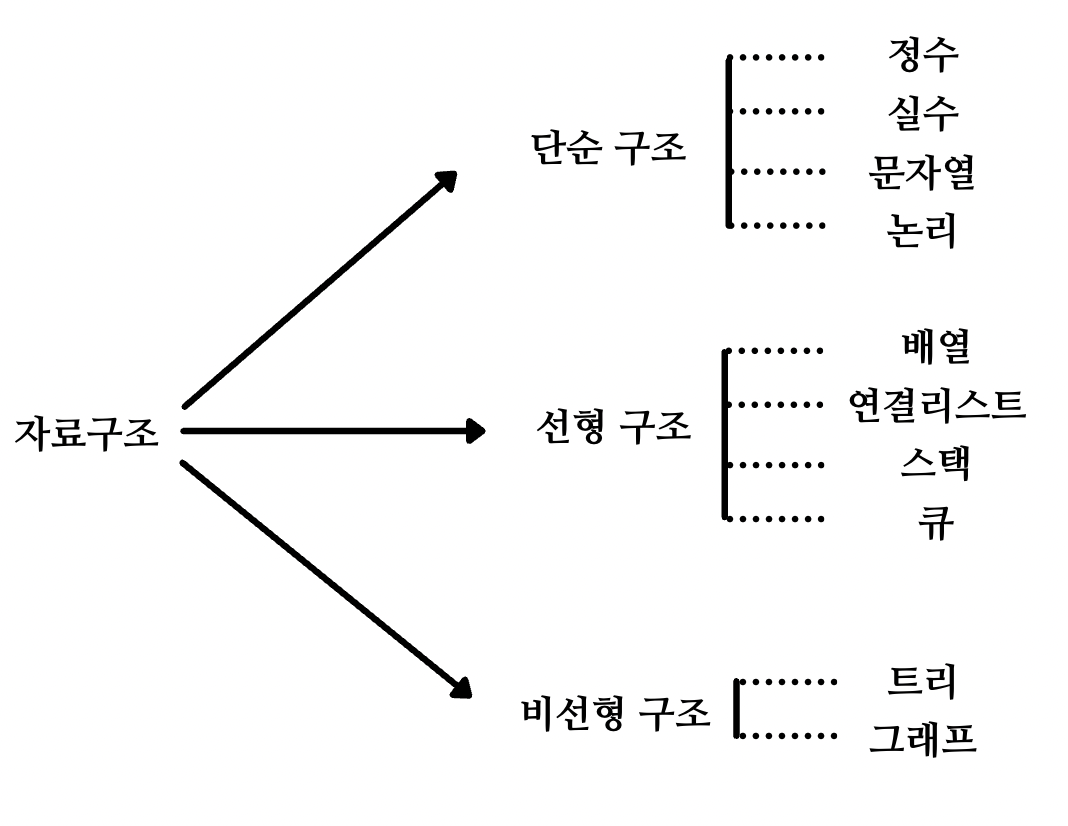
선형구조
한 원소 뒤에 하나의 원소만이 존재하는 형태.
자료들이 선형으로 나열되어 있는 구조를 가진다.
- 배열, 연결리스트(Linked List), 스택, 큐, ...
비선형 구조
원소 간 다대 다 관계를 가지는 구조.
계층적 구조나 망형 구조를 표현하기에 적합.
- 트리, 그래프, ...
시간복잡도
자료구조와 알고리즘을 공부하기 위해 꼭 알아야할 지식!
우리는 프로그램의 성능을 정확하게 파악하기 힘듭니다.
따라서, 대략적인 성능을 비교하기 위한 상대적인 표기법을 사용해야 합니다.
이를 Big-O 표기법(시간 복잡도를 나타내기 위한 방법) 이라고 합니다.
O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^n) < O(n!)
// O(1) 이 가장 빠릅니다!위의 Big-O 표현을 간단히 코드로 나타내자면,
O(n)
for (let i = 0; i < n; i++) {
// ...
}
---
O(log n)
for (let i = 0; i <= n; i *= 2) {
// ...
}
---
O(n log n)
for (let i = 0; i < n; i++) {
for (let j = 1; j <= n; j *= 2) {
// ...
}
}
---
O(n^2)
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// ...
}
}Big-O 표기법의 4가지 법칙
계수 법칙, 합의 법칙, 곱의 법칙, 다항 법칙
계수 법칙
상수 k가 0보다 클 때, f(n) = O(g(n))이면 kf(n) = O(g(n))이다.
즉, k는 생략 가능하다. (n이 무한대에 가까울수록 K의 크기는 의미가 없다.)
합의 법칙
Big-O는 더해질 수 있다.
곱의 법칙
Big-O는 곱해질 수 있다.
다항 법칙
f(n)이 k차 다항식이면 f(n)은 O(n^k)이다 (ex. i < n n n 의 루프 조건을 가진다면, 이 루프는 O(n^3)으로 표기할 수 있다.)
중요한 두 가지만 기억합시다.
1) 상수항은 무시한다. (계수 법칙에 의해 계수 무시)
2) 가장 큰 항 외엔 무시한다. (O(n^2 + n) = O(n^2))
성능 측정 방법
Date 객체 이용
const start = new Date().getTime();
// ...
const end = new Date().getTime();
console.log(end - start);먼저 시작시간을 구하고, 로직을 돌린 다음 끝시간에서 시작시간을 빼주면 로직 작동시간을 알 수 있습니다.
이를 통해 대략적인 성능 측정이 가능합니다.
배열, 순차 리스트 (Array)
배열
연관된 데이터가 연속적인 형태로 구성된 구조.
배열에 포함된 원소는 순서대로 번호(Index)가 붙는다.
배열을 이용하여 연관된 데이터를 하나의 변수에 넣어 처리할 수 있습니다.
배열의 특징
- 고정된 크기를 가지며, 일반적으로 동적으로 크기를 늘릴 수 없다.
(자바스크립트와 같은 대부분의 스크립트 언어는 동적으로 크기가 증감되도록 만들어져 있습니다.) - 원하는 원소의 index 를 알고 있으면 O(1), 상수시간 내로 원소를 찾을 수 있다.
- 원소를 삭제한다면, 해당 index에 빈자리가 생긴다.
배열의 요소를 삭제 / 추가 하고자 한다면?
중간의 값을 삭제한다면, 원소를 삭제한 index 는 빈자리가 되고, 뒤에서 한자리씩 당겨옵니다.
이렇게 삭제 후, 순서를 재정렬하려면 O(n)의 시간이 소요됩니다.
충간에 값을 추가한다면, 맨 뒤의 요소부터 한자리씩 순차적으로 뒤로 밀어냅니다.
넣고자 하는 index 위치가 빈자리가 된다면, 해당 위치에 값을 삽입할 수 있습니다.
배열에 요소를 추가하는 것도 O(n)의 시간이 소요됩니다.
따라서, 이렇게 추가 / 삭제가 반복되는 로직이라면, 배열 사용을 권장하지 않습니다!
배열은 탐색이 많은 경우에 유리한 자료구조입니다.
배열 생성 방법
let arr1 = []; // 빈 Array 배열을 생성합니다.
let arr2 = [1, 2, 3, 4, 5]; // Array 생성과 동시에 초기화 시킬 수 있습니다.
let arr3 = Array(5).fill(0); // fill 을 통해 많은 값으로 초기화 할 수 있습니다. // [0, 0, 0, 0, 0]
let arr4 = Array.from({ length: 10 }, (_, i) => i); // from 을 통해 특정 로직을 사용하여 초기화 할 수 있습니다. // [0, 1, 2, 3, 4, ... , 9]
배열의 요소 추가 / 삭제는 각각 push / splice를 주로 사용합니다.
자바스크립트 배열의 특이점
자바스크립트에서의 배열은 동적으로 작동합니다.
즉, 배열의 크기가 고정되어 있지 않습니다.
자바스크립트의 index는 꼭 number 가 아니여도 됩니다. (String, Boolean 값도 가능합니다.)
그러나 이런 사용법은 추천되지 않습니다.
연결 리스트 (Linked List)
연결 리스트는 추가와 삭제가 반복되는 로직에 적합합니다.
연결 리스트는 각 요소를 포인터로 연결하여 관리하는 선형 자료구조입니다.
각 요소는 노드라고 불리며, 해당 노드의 값인 데이터 영역과 다음 노드를 가리키는 포인터 영역으로 구성됩니다.

출처: https://dojang.io/mod/page/view.php?id=645
연결 리스트의 특징
- 메모리가 허용하는 한, 요소를 제한없이 추가할 수 있다.
- 탐색에는
O(n)이 소요된다. - 요소의 추가 / 제거에는
O(1)이 소요된다. - Singly Linked List(단일 연결 리스트), Doubly Linked List(이중 연결 리스트), Curcular Linked List(원형 연결 리스트) 가 존재한다.
배열과의 차이점
1) 배열은 순차적인 데이터가 들어가므로, 메모리 영역을 연속적으로 사용합니다.
연결 리스트는 순차적이지 않고, 데이터가 담긴 메모리 영역이 퍼져 있습니다. (포인터를 사용하여 각 영역을 참조합니다.)
2) 배열의 요소를 추가 / 제거 하기 위해서는 선형시간 O(n) 이 소요됩니다.
연결 리스트의 요소 추가는 추가할 요소의 포인터를 다음 위치의 요소에 연결합니다. 이어서, 추가될 요소의 바로 전 요소의 포인터를 추가될 요소로 수정합니다. 이는 O(1) 이 소요됩니다.
연결 리스트의 요소 제거는 제거할 요소의 이전 요소가 가르키는 포인터를 제거할 요소 다음 요소에 연결한 후 제거합니다. 이는 O(1) 이 소요됩니다.
요소 찾기
연결 리스트에서 찾기는 Head 포인터에서 시작합니다.
Head 포인터에 연결되어 있는 요소에서 원하는 값을 찾습니다.
원하는 값이 해당 요소에 없다면, 해당 요소의 포인터 영역을 통해 다음 요소로 넘어갑니다.
만약 요소에서 원하는 값을 찾았다면, 로직은 종료됩니다.
이 로직은 O(n)의 시간이 소요됩니다.
연결 리스트에서 요소의 추가 / 제거는
O(1)이 소요되지만, 요소의 탐색은O(n)
이 소요됩니다.
따라서, 추가 / 제거를 를 위해 탐색을 실행하지 않도록 주의해아여야 합니다!
Singly Linked List (단일 연결 리스트)
Head 에서 Tail 까지 단방향으로 이어지는 연결 리스트로, 가장 단순한 형태의 연결 리스트다.
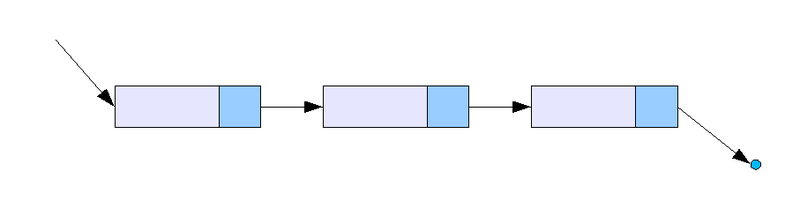
출처: https://ko.wikipedia.org/wiki/연결_리스트
SinglyLinkedList 클래스에 리스트 크기를 구하는 'size' 메소드를 만들어 봅시다.
만들어진 SinglyLinkedList 는 예외 처리가 되어 있지 않습니다. 예외가 발생해도 동작할 수 있도록 모든 예외를 찾아 수정해봅시다.
Doubly Linked List (이중 연결 리스트)
양뱡향으로 이어지는 연결리스트로, 단일 연결 리스트보다 자료구조의 크기가 좀 더 크다.
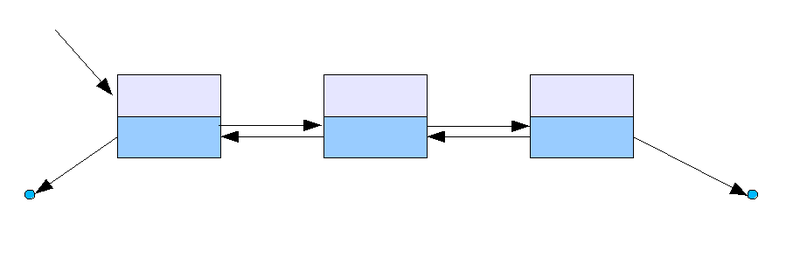
출처: https://ko.wikipedia.org/wiki/연결_리스트
SinglyLinkedList 클래스를 참고하여 DoublyLinkedList를 구현해 봅시다.
Circular Linked List (환형 연결 리스트)
단일 혹은 이중 연결 리스트에서 Tail이 Head로 연결되는 연결 리스트로, 메모리를 아껴 쓸 수 있으며 원형 큐 등을 만들 때에도 사용된다.
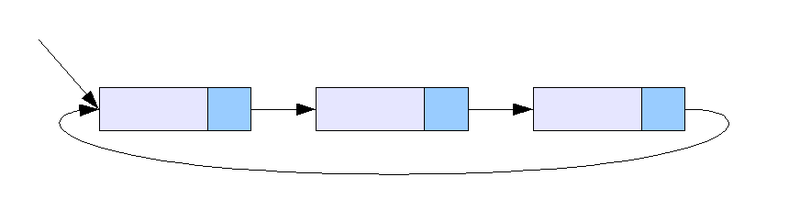
출처: https://ko.wikipedia.org/wiki/연결_리스트
SinglyLinkedList 클래스를 참고하여 CircularLinkedList를 구현해 봅시다.
(탐색 종료 조건이 있어야 합니다.)
연결 리스트는 이제껏 실제로 응용하여 써본 적이 없는데, 어떤 상황에서 유용하게 쓸 수 있는지 알 수 있었습니다.
알고리즘 문제를 풀 때 배열로 모든 걸 해결하면서 풀어갔는데 요소 추가 / 제거가 잦은 문제는 활용해보도록 연습해보려고 합니다.
그리고 시간복잡도때문에 코딩테스트 시간초과가 났던 경험이 많이 있었기 때문에 복잡도를 줄이는 공부를 많이 할 계획입니다.
자료구조를 알맞게 활용하는 능력이 아직 많이 부족한데, 결국 문제를 많이 풀어보는게 해답인 것 같습니다.. 😭

