Tree의 정의
자료구조 Tree는 이름 그대로 나무의 형태를 가지고 있습니다. 정확히는 나무를 거꾸로 뒤집어 놓은 듯한 모습을 가지고 있습니다. 그래프의 여러 구조 중 단방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮았다고 해서 트리 구조라고 부릅니다.
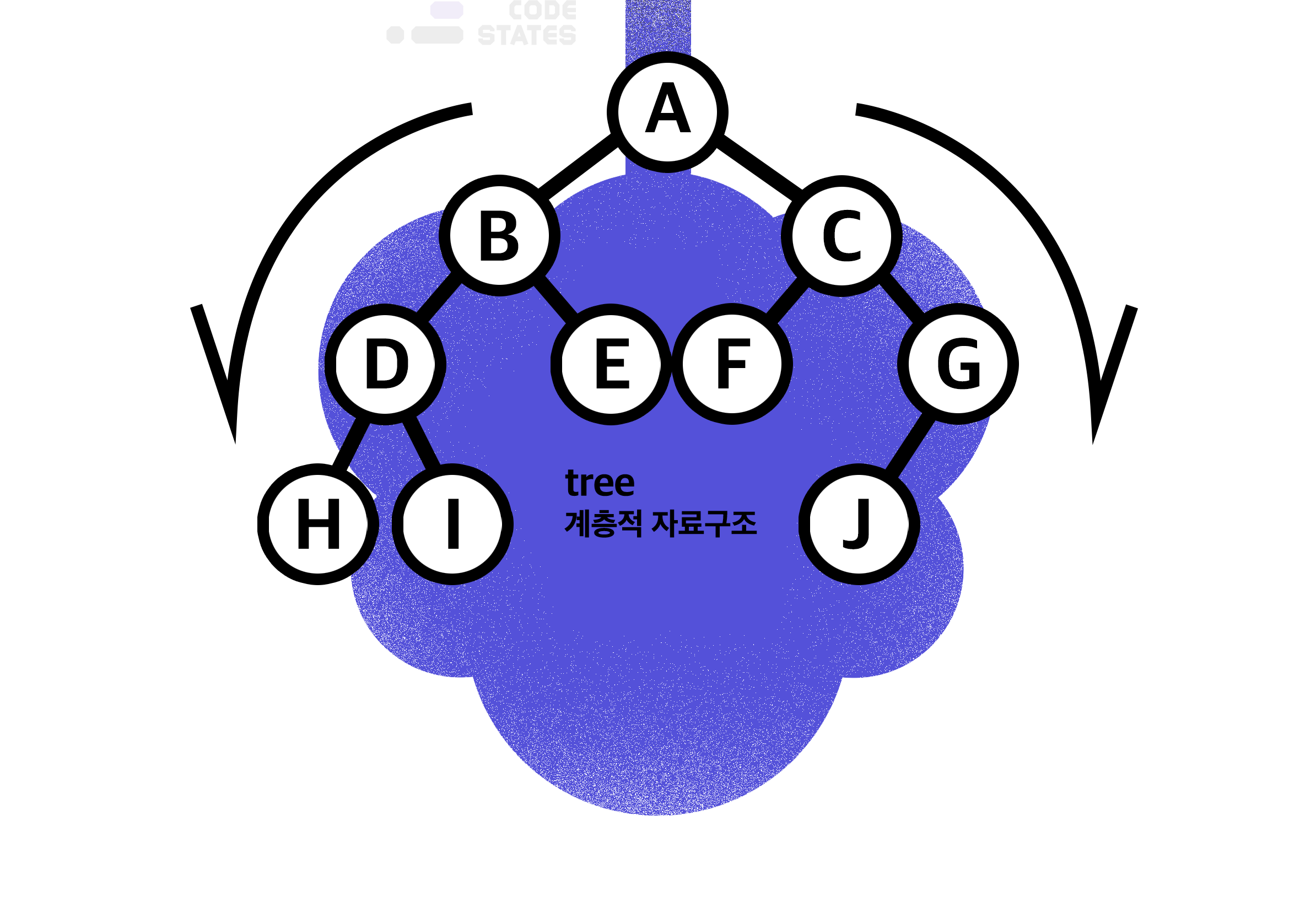
마치 가계도와 흡사해 보이는 이 트리 구조는 데이터가 바로 아래에 있는 하나 이상의 데이터에 한 개의 경로와 하나의 방향으로만 연결된 계층적 자료구조입니다.
데이터를 순차적으로 나열시킨 선형 구조가 아니라, 하나의 데이터 아래에 여러 개의 데이터가 존재할 수 있는 비선형 구조입니다.
트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가기 때문에 사이클(cycle)이 없습니다.
여기서 사이클이란 시작 노드에서 출발해 다른 노드를 거쳐 시작 노드로 돌아올 수 있다면 사이클이 존재한다고 표현합니다. 따라서 트리는 사이클(cycle)이 없는 하나의 연결 그래프 (Connected Graph)라고 할 수 있습니다.
Tree의 구조와 특징
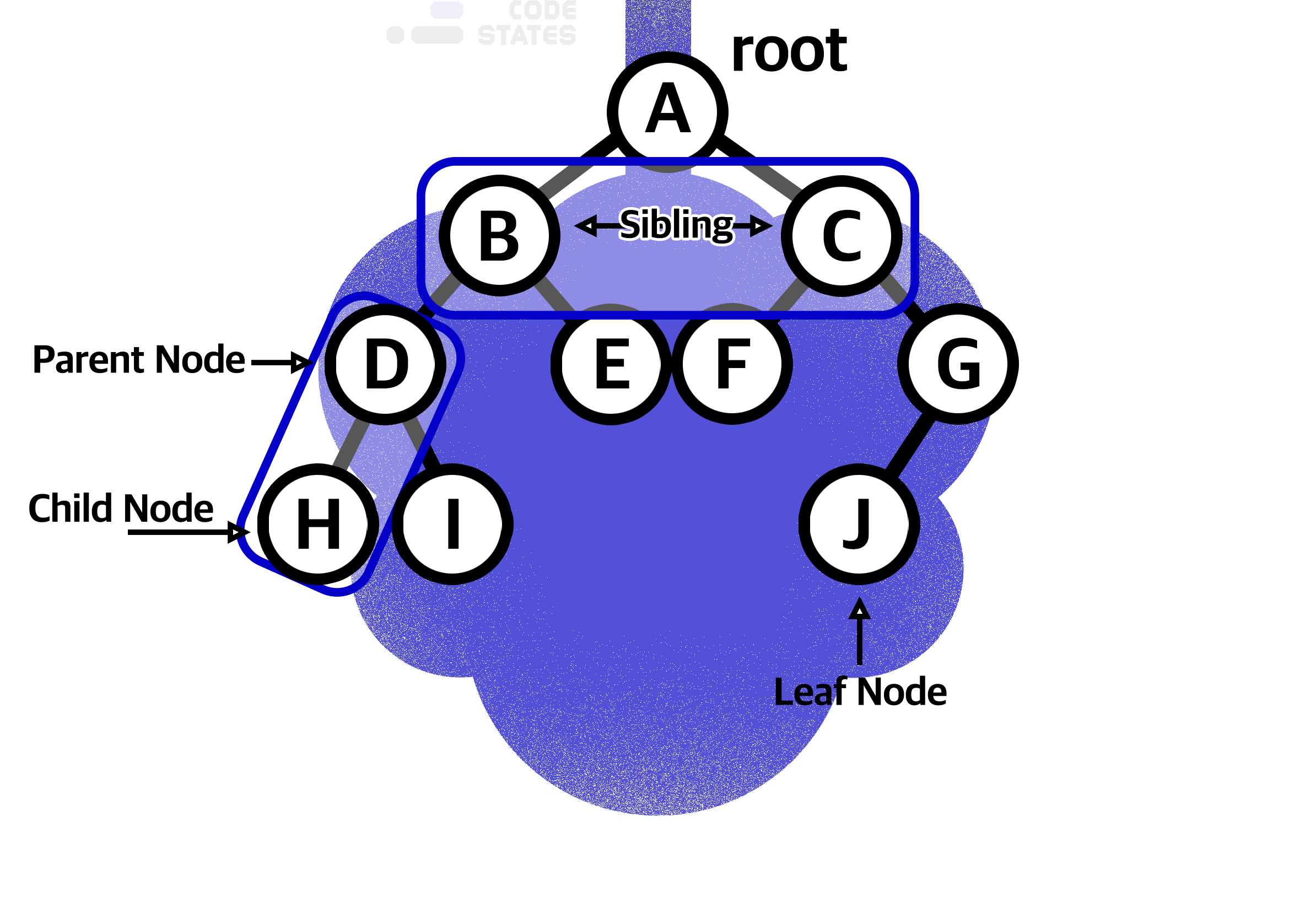
트리 구조는 루트(Root)라는 하나의 꼭짓점 데이터를 시작으로 여러 개의 데이터를 간선(edge)으로 연결합니다. 각 데이터를 노드(Node)라고 하며, 두 개의 노드가 상하 계층으로 연결되면 부모/자식 관계를 맺습니다. 위 그림에서 A는 B와 C의 부모 노드(Parent Node)이고, B와 C는 A의 자식 노드(Child Node)입니다. 자식이 없는 노드는 나무의 잎과 같다고 하여 리프 노드(Leaf Node)라고 부릅니다.
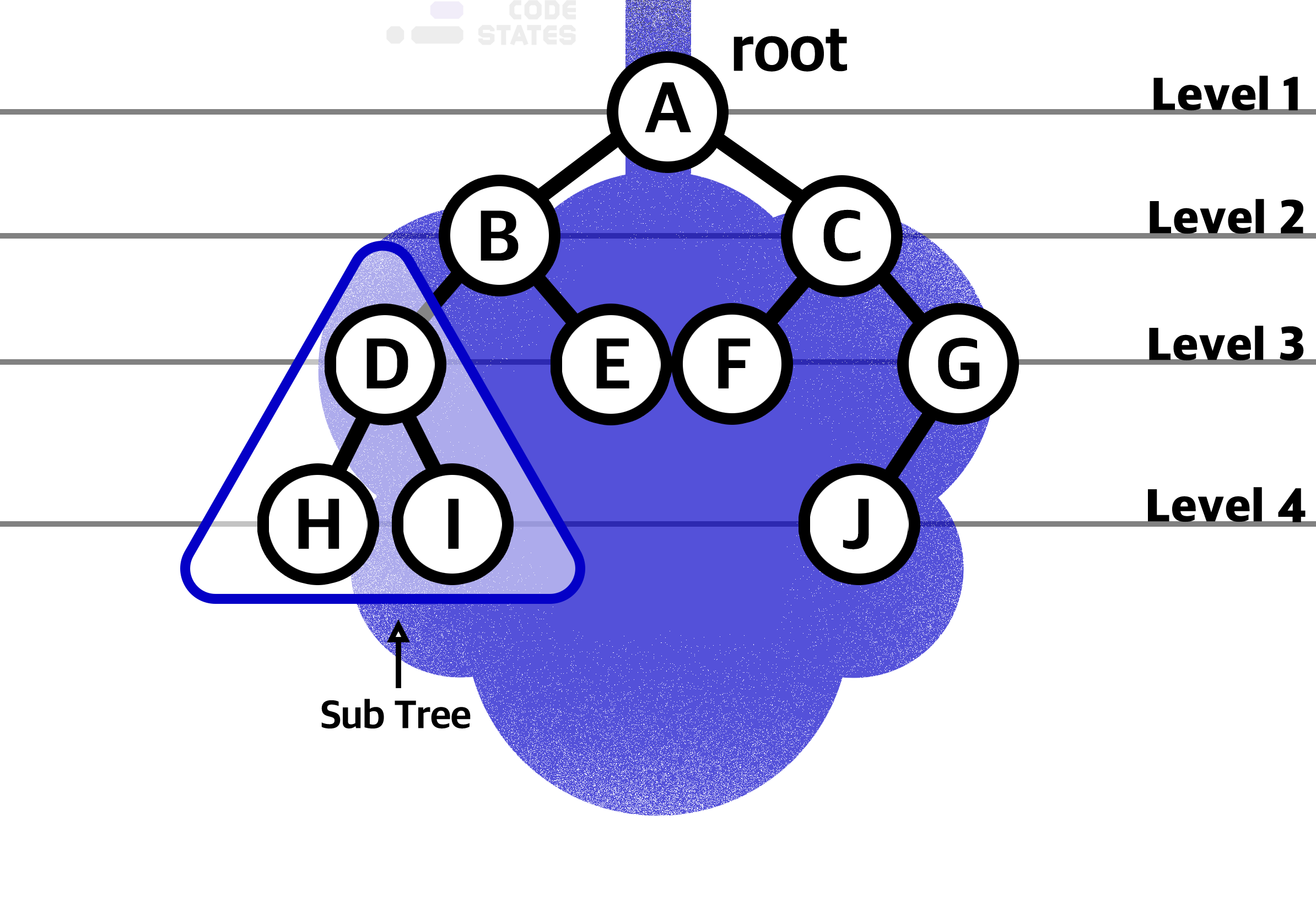
자료구조 Tree는 깊이와 높이, 레벨 등을 측정할 수 있습니다.
깊이 (depth)
트리 구조에서는 루트로부터 하위 계층의 특정 노드까지의 깊이(depth)를 표현할 수 있습니다. 루트 노드는 지면에 있는 것처럼 깊이가 0입니다. 위 그림에서 루트 A의 깊이는 0이고, B와 C의 깊이는 1입니다. D, E, F, G의 깊이는 2입니다.
레벨(Level)
트리 구조에서 같은 깊이를 가지고 있는 노드를 묶어서 레벨(level)로 표현할 수 있습니다. 깊이가 0인 루트 A의 level은 1입니다. 깊이가 1인 B와 C의 level은 2입니다. D, E, F, G의 레벨은 3입니다. 같은 레벨에 나란히 있는 노드를 형제 노드(Sibling Node)라고 합니다.
높이(Height)
트리 구조에서 리프 노드를 기준으로 루트까지의 높이(height)를 표현할 수 있습니다. 리프 노드와 직간접적으로 연결된 노드의 높이를 표현하며, 부모 노드는 자식 노드의 가장 높은 높이 값에 +1한 값을 높이로 가집니다.
트리 구조의 높이를 표현할 때는 각 리프 노드의 높이를 0으로 놓습니다. 위 그림에서 H, I, E, F, J의 높이는 0입니다. D와 G의 높이는 1입니다. B와 C의 높이는 2입니다. 이때 B는 D의 height + 1을, C는 G의 height + 1을 높이로 가집니다. 따라서, 루트 A의 높이는 3입니다.
서브 트리(Sub tree)
트리 구조의 루트에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리를 서브 트리라고 부릅니다. (D, H, I)로 이루어진 작은 트리도 서브 트리이고, (B, D, E)나 (C, F, G, J)도 서브 트리입니다.
자료구조는 자료의 집합을 구조화하고, 이를 표현하는 데에 초점이 맞춰져 있습니다. 여러분은 이미 자료구조를 알게 모르게 많이 접했습니다. 사람이 자료를 사용하기에 편리하도록 만들어진 것이 자료구조이기 때문입니다.
용어정리
-
노드(Node) : 트리 구조를 이루는 모든 개별 데이터
-
루트(Root) : 트리 구조의 시작점이 되는 노드
-
부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
-
자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
-
리프(Leaf) : 트리 구조의 끝 지점이고, 자식 노드가 없는 노드
Tree의 실사용 예제
가장 대표적인 예제는 컴퓨터의 디렉토리 구조입니다. 어떤 프로그램이나 파일을 찾을 때, 바탕화면 폴더나 다운로드 폴더 등에서 다른 폴더에 진입하고, 또 그 안에서 다른 폴더에 진입하면서 원하는 프로그램이나 파일을 찾습니다. 모든 폴더는 하나의 폴더(루트 폴더, /)에서 시작되어, 가지를 뻗어나가는 모양새를 띕니다.
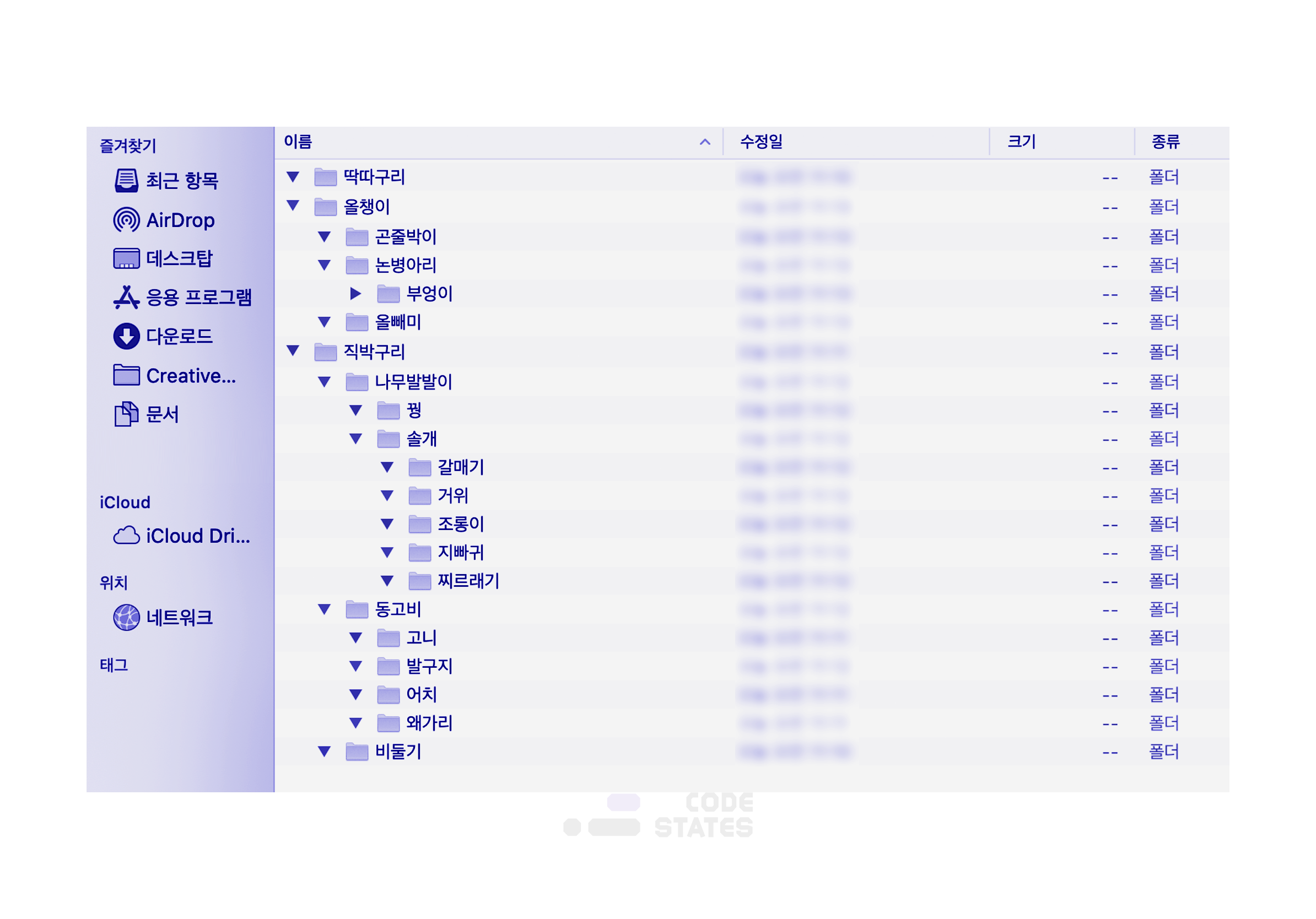
하나의 폴더 안에 여러 개의 폴더가 있고, 또 그 여러 개의 폴더 안에 또 다른 폴더나 파일이 있습니다. 위 그림처럼, 제일 첫 번째 폴더에서 출발하여 도착하려는 폴더로 가는 경로는 유일합니다. 사용자들이 편하게 사용하기 위한 파일 시스템 등에서는 트리 구조를 이용해 만들어져 있습니다.
이진트리(Binary tree)
먼저, 이진트리(Binary tree)는 자식 노드가 최대 두 개인 노드로 구성된 트리입니다. 이 두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있습니다.
이진트리는 자료의 삽입, 삭제 방법에 따라 정 이진트리(Full binary tree), 완전 이진트리(Complete binary tree), 포화 이진트리(Perfect binary tree)로 나뉩니다.
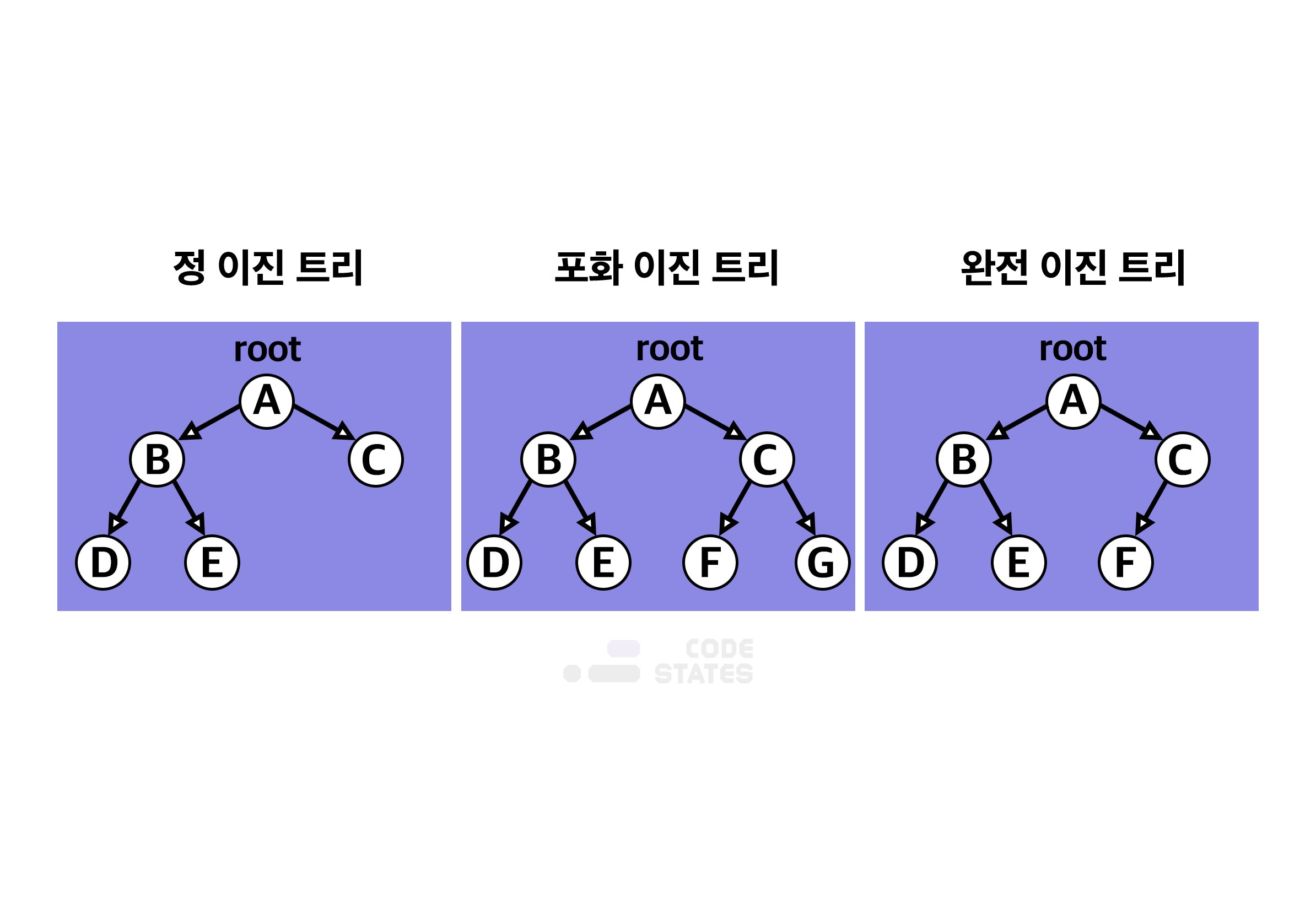
이진트리 특징
이진트리는 아래와 같은 특징이 있습니다.
-
정 이진트리(Full binary tree) : 각 노드가 0개 혹은 2개의 자식 노드를 갖습니다.
-
포화 이진트리(Perfect binary tree) : 정 이진트리이면서 완전 이진트리인 경우입니다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리입니다.
-
완전 이진트리(Complete binary tree) : 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 합니다.
이러한 이진트리는 이진 탐색 트리와 이진 힙 구현에 사용되며, 효율적인 검색과 정렬을 위해 사용됩니다.
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리란 이진 탐색의 속성이 이진트리에 적용된 특별한 형태의 이진트리입니다.
먼저 이진 탐색이 무엇인지 간단히 살펴보도록 하겠습니다
이진 탐색이란
이진 탐색 알고리즘이란 정렬된 데이터 중에서 특정한 값을 찾기 위한 탐색 알고리즘 중 하나입니다.
이진 탐색 알고리즘은 오름차순으로 정렬된 정수의 배열을 같은 크기의 두 부분 배열로 나눈 후, 두 부분 중 탐색이 필요한 부분에서만 탐색하도록 탐색 범위를 제한하여 원하는 값을 찾는 알고리즘입니다.
- 배열의 중간에 내가 찾고자 하는 값이 있는지 확인한다.
- 중간값이 내가 찾고자 하는 값이 아닐 경우, 오름차순으로 정렬된 배열에서 중간값보다 큰 값인지 작은 값인지 판단한다.
- 찾고자 하는 값이 중간값보다 작은 값일 경우, 배열의 맨 앞부터 중간값 전까지의 범위를 탐색 범위로 잡고 탐색을 반복 수행한다.
- 찾고자 하는 값이 중간값보다 큰 값일 경우, 배열의 중간값의 다음 값부터 맨 마지막까지를 탐색 범위로 잡고 탐색을 반복 수행한다.
이진 탐색 트리는 이러한 이진 탐색의 알고리즘이 이진트리에 적용된 형태로 트리의 루트노드는 이진 탐색에서 리스트의 중간값이 됩니다.
루트노드의 왼편 서브 트리의 값들은 이진 탐색 알고리즘에 기반하여 모두 루트노드의 값보다 작은 값들이 자리 잡고 있고 루트노드의 오른편 서브 트리의 값들은 루트노드의 값보다 큰 값들이 자리 잡고 있어야 합니다.
정리해 보면 이진탐색트리는 다음과 같은 특징을 가지고 있습니다.
- 각 노드에 중복되지 않는 키(Key)가 있습니다.
- 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있습니다.
- 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있습니다.
- 좌우 서브 트리도 모두 이진 탐색 트리여야 합니다.
즉 이진 탐색 트리(Binary Search Tree)는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있습니다. 예를 들어서 다음과 같은 트리가 이진 탐색 트리입니다.
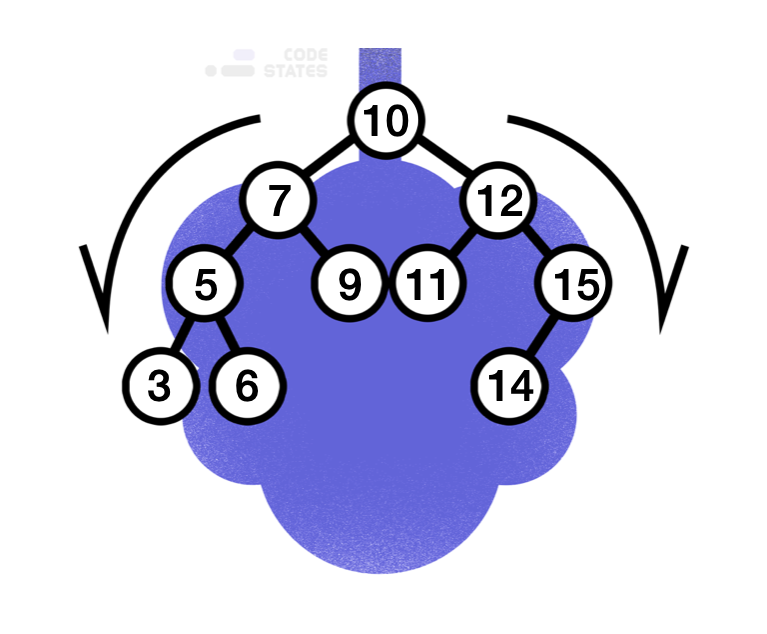
이진 탐색 트리는 균형 잡힌 트리가 아닐 때, 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있습니다.
균형이 잡히지 않은 트리는 탐색하는 데 시간이 더 걸리는 경우도 있기 때문에 해결해야 할 문제입니다. 이 문제를 해결하기 위해 삽입과 삭제마다 트리의 구조를 재조정하는 과정을 거치는 알고리즘을 추가할 수 있습니다.
이진 탐색 트리 특징
이진 탐색 트리는 기존 이진트리보다 탐색이 빠르다는 장점이 있습니다. 이진 탐색 트리의 연산은 트리의 높이가 h(height)라면 o(h)의 복잡도를 가지게 됩니다. 이와 같은 효율적인 연산이 가능한 이유는 탐색 과정에 있습니다.
이진 탐색 트리의 탐색은 다음과 같은 과정을 거칩니다.
-
루트 노드의 키와 찾고자 하는 값을 비교합니다. 만약 찾고자 하는 값이라면 탐색을 종료합니다.
-
찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행합니다.
-
찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행합니다.
이 과정을 찾고자 하는 값을 찾을 때까지 반복해 진행합니다. 만약 값을 찾지 못한다면 그대로 연산을 종료하게 됩니다. 이러한 탐색 과정을 거치면 최대 트리의 높이(h)만큼 탐색을 진행합니다.
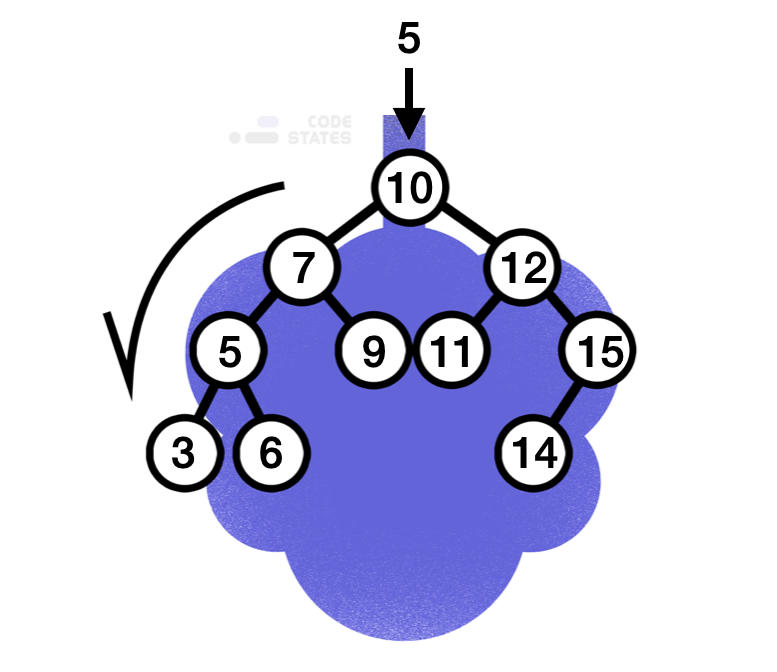
만약 이와 같은 트리에서 5라는 값을 찾고자 하면 제일 처음에는 루트 노드와 값을 비교하게 됩니다. 루트 노드가 여기서는 10이므로 루트 노드보다 작기 때문에, 왼쪽 서브 트리로 탐색을 시작합니다.
이후 마주친 노드는 7이고, 찾고자 하는 값은 5이므로 다시 7을 기준으로 왼쪽 서브 트리로 탐색을 진행합니다. 이어 만난 값이 찾고자 하는 값이므로 탐색이 종료됩니다. 10부터 5까지 3번의 탐색이 이뤄졌지만, 만약 3을 찾는다면 4번의 연산이 진행되었을 것입니다. 즉 트리 안의 값을 찾는다면 무조건 트리의 높이(h) 이하의 탐색이 이뤄지게 됩니다.
여기서 하나 알아둬야 할 점은, 트리 안에 찾고자 하는 값이 없더라도 최대 h번(트리의 높이) 만큼의 연산 및 탐색이 진행된다는 것입니다. 만일 13이라는 숫자를 찾는다고 가정해 봅시다.
마지막으로 도착하는 노드의 값은 14인데, 여기서 13은 14보다 작으므로 왼쪽 서브 트리로 탐색을 진행해야 합니다. 그런데 오른쪽 서브 트리가 없으므로 14에서 탐색이 종료 되게 됩니다. 그렇기 때문에 트리 안에 찾고자 하는 값이 없더라도 최대 h번의 연산 및 탐색이 진행되게 되는 것입니다.
트리 순회
특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것을 트리 순회라고 합니다.
트리 구조는 계층적 구조라는 특별한 특징을 가지기 때문에, 모든 노드를 순회하는 방법엔 크게 세 가지가 있습니다.
트리를 순회할 수 있는 세 가지 방법은 전위 순회, 중위 순회, 후위 순회입니다.
이 순회 방식들은 모두 노드를 순회할 때 왼쪽부터 오른쪽으로 조회한다는 공통점이 있습니다.
각 순회 방식의 차이점에 대해서도 알아보겠습니다.
전위 순회 (preorder traverse)

전위 순회에서 가장 먼저 방문하는 노드는 루트입니다. 루트에서 시작해 왼쪽의 노드들을 순차적으로 둘러본 뒤, 왼쪽의 노드 탐색이 끝나면 오른쪽 노드를 탐색합니다. 즉 부모 노드가 제일 먼저 방문되는 순회 방식입니다. 전위 순회는 주로 트리를 복사할 때 사용합니다.
중위 순회 (inorder traverse)

중위 순회는 루트를 가운데에 두고 순회합니다. 제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 기준으로 왼쪽에 있는 노드의 순회가 끝나면 루트를 거쳐 오른쪽에 있는 노드로 이동하여 마저 탐색합니다. 부모 노드가 서브 트리의 방문 중간에 방문되는 순회 방식입니다. 중위 순회는 이진 탐색 트리의 오름차순으로 값을 가져올 때 쓰입니다.
후위 순회 (postorder traverse)

후위 순회는 루트를 가장 마지막에 순회합니다. 제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 거치지 않고 오른쪽으로 이동해 순회한 뒤, 제일 마지막에 루트를 방문합니다. 후위 순회는 트리를 삭제할 때 사용합니다. 자식 노드가 먼저 삭제되어야 상위 노드를 삭제할 수 있기 때문입니다.
레벨 순회 (levelorder traverse)
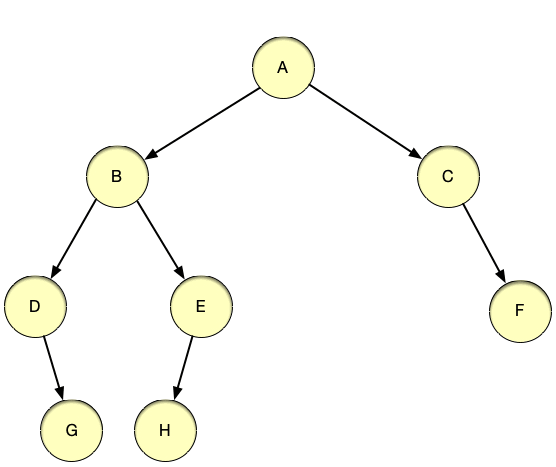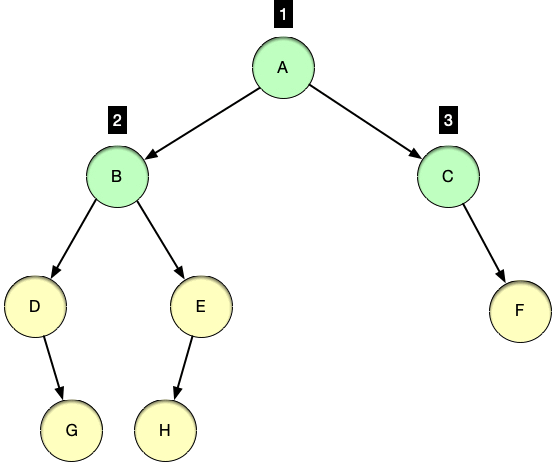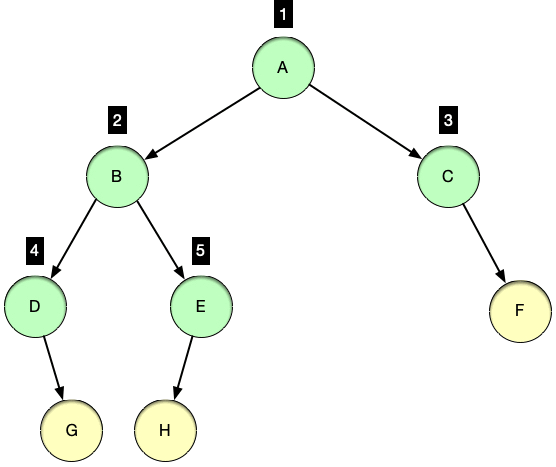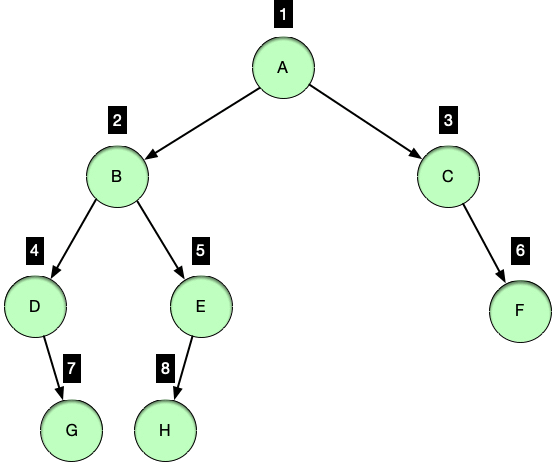
레벨 순회는 루트를 방문하는 기준으로 순회를 하는 것이 아닌 트리의 레벨 기준으로 노드들을 방문하는 순회 방법입니다.
루트 노드를 시작으로 아래로 뻗어나가며 노드들을 방문하며 루트 노드의 레벨이 1이라고 했을 때 아래로 내려갈수록 레벨은 증가하는 특징을 보입니다.
동일한 레벨에 여러 노드가 존재할 경우 왼쪽에서 오른쪽 순서로 노드를 방문합니다.
순회 방식을 나누는 이유
앞서 배운 이진트리 탐색의 경우는 간단한 편이지만 순회 방법은 조금 복잡한 편입니다. 일정 조건에 의해 설계된 트리 구조는 자식 노드에 대한 조건이 명확하다면 원하는 값을 쉽게 찾아낼 수 있게 되지만, 트리 구조 전체를 탐색할 때는 이야기가 조금 달라지기 때문입니다. 모든 노드를 방문하기 위해서는 일정한 조건이 필요하고, 트리 구조를 유지보수하거나 특정 목적을 위해서도 순회 방법에 대한 정의는 필수적으로 필요합니다.
Graph의 정의
그래프는 여러 개의 점이 서로 복잡하게 연결된 관계를 표현한 자료구조입니다.
그래프라는 단어를 들으면 어떤 그림이 떠오르나요? 자료구조의 그래프를 처음 접한다면, 아마 대부분의 사람은 아래의 그림처럼 생긴 그래프를 떠올릴 겁니다.

X축과 Y축이 존재하고, X축의 값에 따라 Y축의 값을 나타내는 그래프, 또는 수학 수업이나 발표에서 사용되는 자료로 자주 접한 이 그래프를 말입니다.
그러나 컴퓨터 공학에서 이야기하는 자료구조 그래프는 전혀 다른 모습을 가지고 있습니다. 자료구조의 그래프는 마치 거미줄처럼 여러 개의 점이 선으로 이어져 있는 복잡한 네트워크망과 같은 모습을 가지고 있습니다.
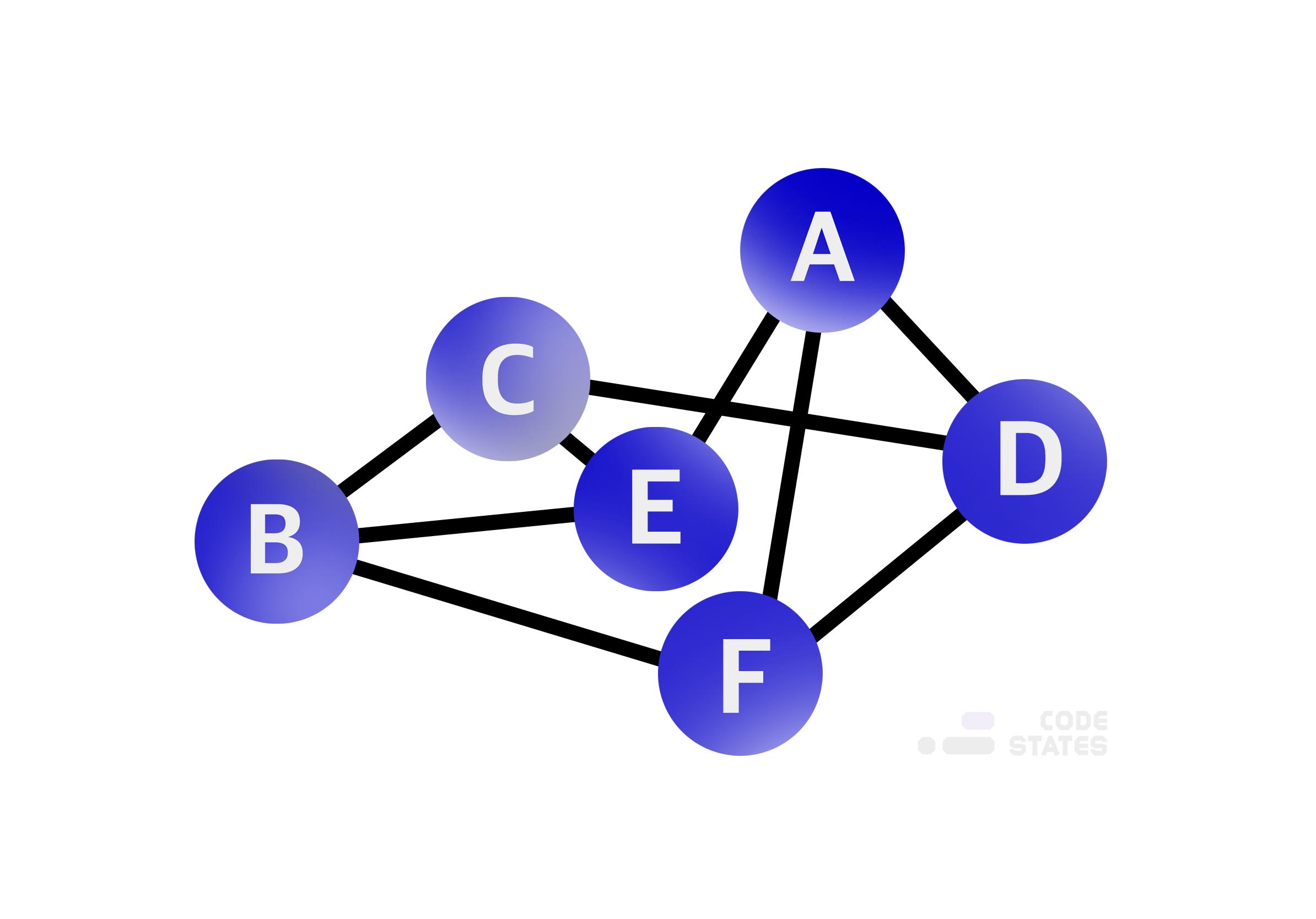
Graph의 구조
- 직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 있습니다.
- 간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어집니다.
- 하나의 점을 그래프에서는 정점(vertex)이라고 표현하고, 하나의 선은 간선(edge)이라고 합니다.
다음 그림은 간단한 그래프입니다. 각각이 무엇인지 살펴보세요.
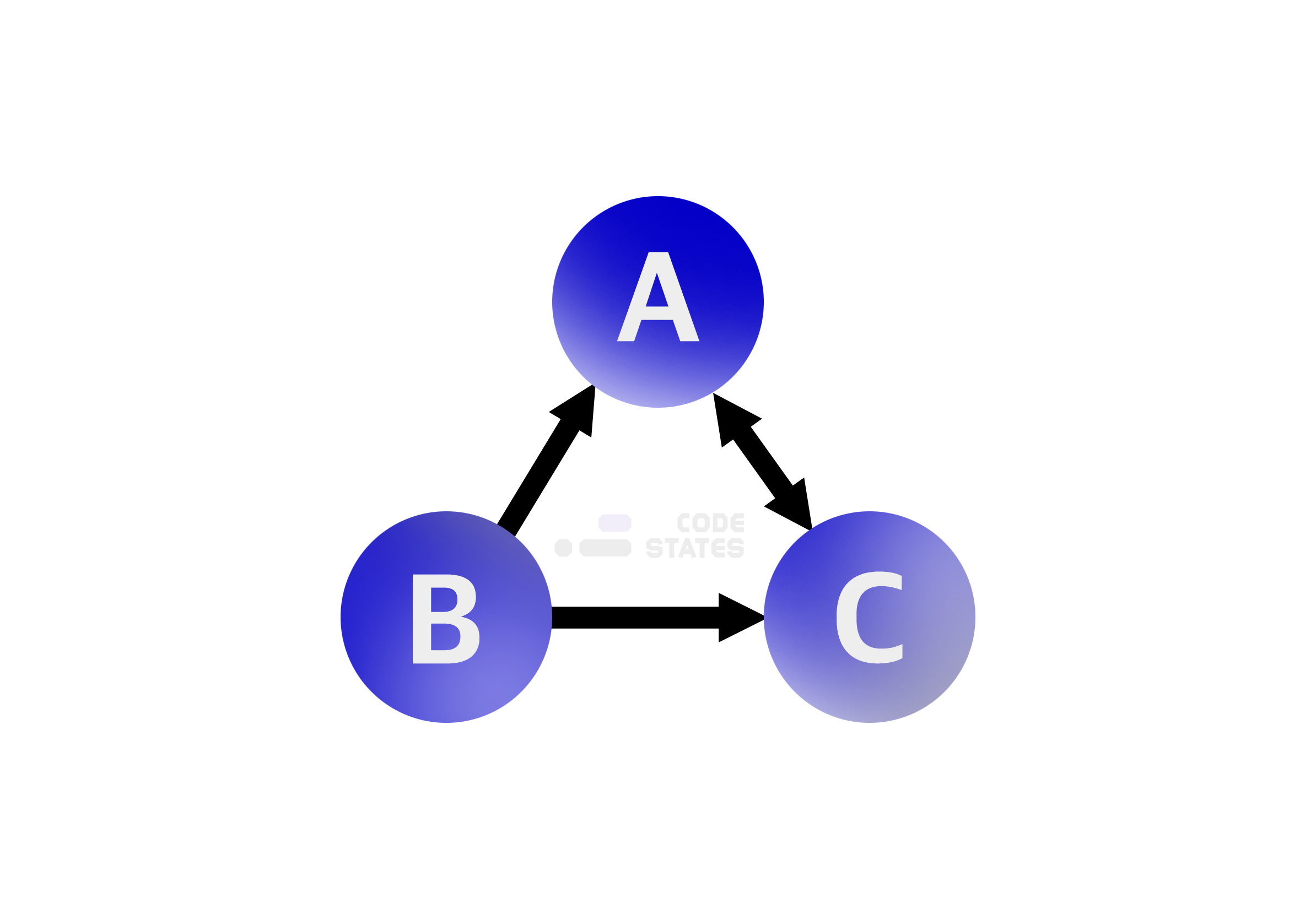
Graph의 표현 방식
인접 행렬
두 정점을 바로 이어주는 간선이 있다면 이 두 정점은 인접하다고 이야기합니다. 인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로 2차원 배열의 형태로 나타냅니다. 만약 A라는 정점과 B라는 정점이 이어져 있다면 1(true), 이어져 있지 않다면 0(false)으로 표시한 일종의 표입니다. 만약 가중치 그래프라면 1 대신 관계에서 의미 있는 값을 저장합니다.
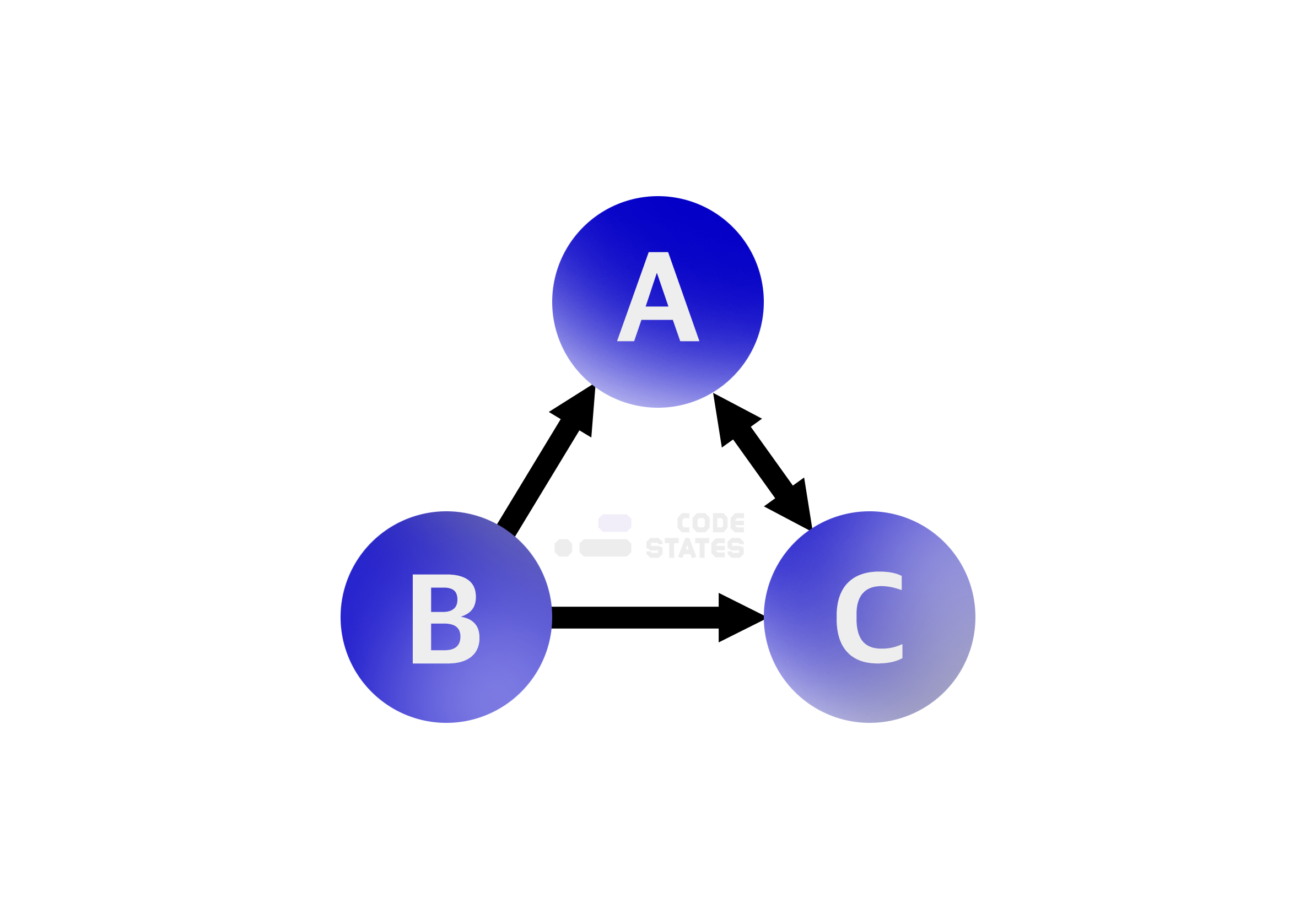
- A의 진출차수는 1개입니다: A —> C
[0][2] === 1 // A([0])는 C([2])로 가는 진출차수가 있다(1)- B의 진출차수는 2개입니다: B —> A, B —> C
[1][0] === 1 // B([1])는 A([0])로 가는 진출차수가 있다(1)
[1][2] === 1 // B([1])는 C([2])로 가는 진출차수가 있다(1)- C의 진출차수는 1개입니다: C —> A
[2][0] === 1 // C([2])는 A([0])로 가는 진출차수가 있다(1)인접 리스트
인접 리스트는 각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 표현합니다. 각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있습니다. 위 그래프를 인접 리스트로 표현하면 다음 그림과 같습니다.
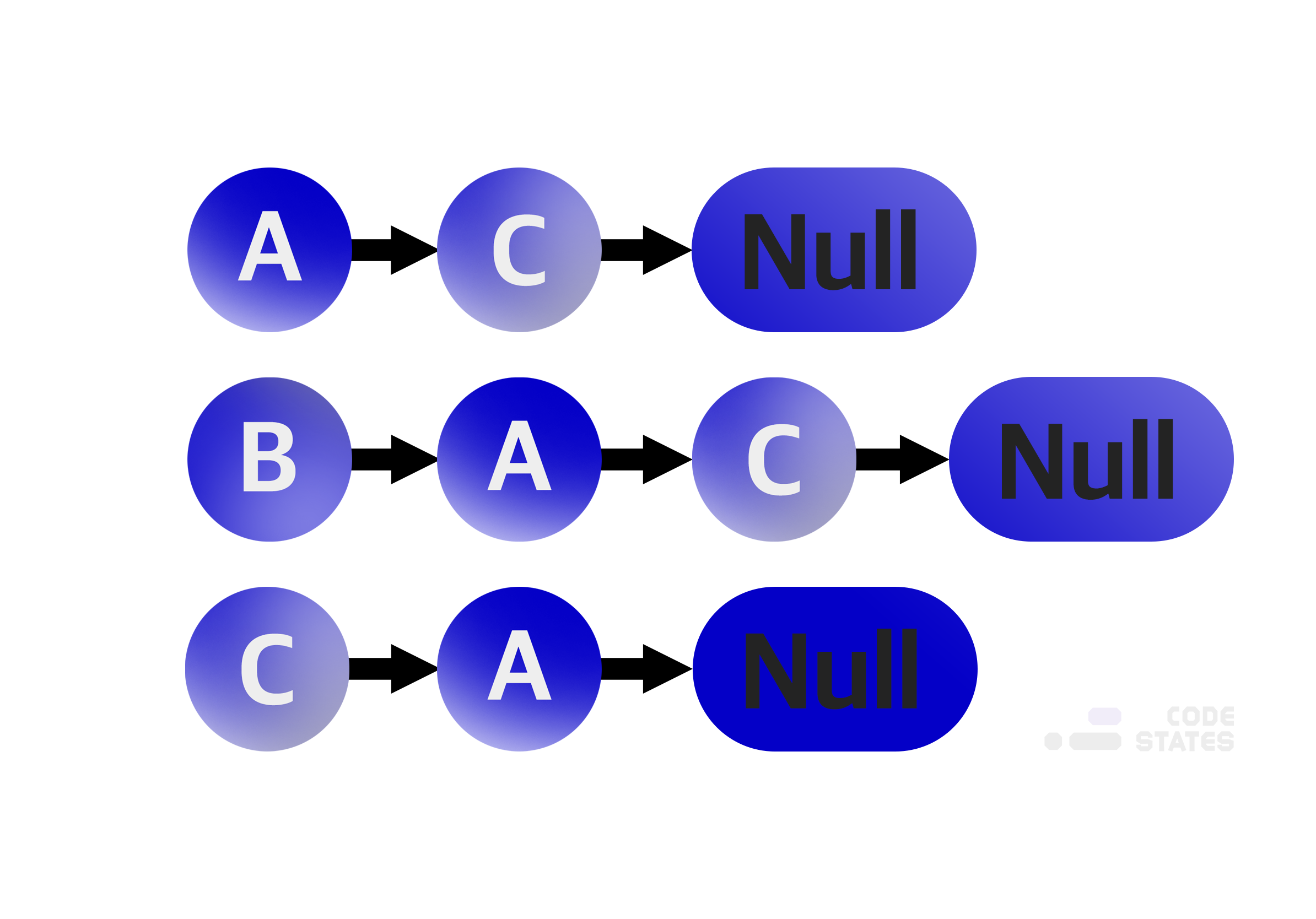
B는 A와 C로 이어지는 간선이 두 개가 있는데, 왜 A가 C보다 먼저죠? 이 순서는 중요한가요?
보통은 중요하지 않습니다. 그래프, 트리, 스택, 큐 등 모든 자료구조는 구현하는 사람의 편의와 목적에 따라 기능을 추가/삭제할 수 있습니다. 그래프를 인접 리스트로 구현할 때, 정점별로 살펴봐야 할 우선순위를 고려해 구현할 수 있습니다. 이때, 리스트에 담긴 정점들을 우선순위별로 정렬할 수 있습니다. 우선순위가 없다면, 연결된 정점들을 단순하게 나열한 리스트가 됩니다.
- 우선순위를 다뤄야 한다면 더 적합한 자료구조(ex. queue, heap)를 사용하는 것이 합리적입니다. 따라서 보통은 중요하지 않습니다. (언제나 예외는 있습니다.)
인접 행렬과 인접 리스트는 각각 언제 사용할까?
[인접 행렬]
1. 한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이합니다.
- 예를 들어, A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0번째 줄의 1번째 열에 어떤 값이 저장되어있는지 바로 확인할 수 있습니다.
2. 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용됩니다.
- 최단 경로를 구하는 과정(BFS)에서는 그래프 탐색이 빈번하게 발생하는데, 이때 인접행렬이 인접리스트에 비해 조회 성능이 우수합니다.
인접행렬의 경우 인덱스를 직접 접근하여 조회가 O(1)로 이루어지기 때문입니다.
반면, 인접리스트의 경우 각 row를 선형 조회해야 하므로 노드의 수가 N일 경우 O(N)의 시간이 소요됩니다.
정리하자면, 인접리스트의 경우 A 노드에서 B 노드로 이동하는 경우만 해도 O(N)의 시간이 소요되며, 더불어 최단 경로를 구하는 과정 자체에서도 시간이 많이 소요되기 때문에
인덱스를 통한 직접 접근이 가능한 인접행렬이 최단경로를 찾는 데 더 유리한 측면이 있다는 것입니다.
[인접 리스트]
1. 메모리를 효율적으로 사용하고 싶을 때 인접 리스트를 사용합니다.
- 인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지합니다.알아둬야 할 Graph 용어들
-
정점 (vertex): 노드(node)라고도 하며 데이터가 저장되는 그래프의 기본 원소입니다.
-
간선 (edge): 정점 간의 관계를 나타냅니다. (정점을 이어주는 선)
-
인접 정점 (adjacent vertex): 하나의 정점에서 간선에 의해 직접 연결된 정점을 뜻합니다.
-
가중치 그래프 (weighted Graph): 연결의 강도(추가적인 정보, ex. 서울-부산으로 가는 거리 등)가 얼마나 되는지 적혀 있는 그래프를 뜻합니다.
-
비 가중치 그래프 (unweighted Graph): 연결의 강도가 적혀 있지 않는 그래프를 뜻합니다.
-
무향(무방향) 그래프 (undirected graph): 앞서 보았던 내비게이션 예제는 무향(무방향) 그래프입니다. 서울에서 부산으로 갈 수 있듯, 반대로 부산에서 서울로 가는 것도 가능합니다. 하지만 단방향(directed) 그래프로 구현된다면 서울에서 부산으로 갈 수 있지만, 부산에서 서울로 가는 것은 불가능합니다(혹은 그 반대). 만약 두 지점이 일방통행 도로로 이어져 있다면 단방향인 간선으로 표현할 수 있습니다.
-
진입차수 (in-degree) / 진출차수 (out-degree): 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타냅니다.
-
인접 (adjacency): 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점입니다.
-
자기 루프 (self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다라고 표현합니다. 다른 정점을 거치지 않는다는 것이 특징입니다.
-
사이클 (cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현합니다. 내비게이션 그래프는 서울 —> 대전 —> 부산 —> 서울로 이동이 가능하므로, 사이클이 존재하는 그래프입니다.
BFS와 DFS
그래프의 탐색은 하나의 정점에서 시작하여 그래프의 모든 정점을 한 번씩 방문(탐색)하는 것이 목적입니다. 그래프의 데이터는 배열처럼 정렬이 되어 있지 않습니다. 그래서 원하는 자료를 찾으려면, 하나씩 모두 방문하여 찾아야 합니다.
지하철 노선도를 보여주는 애플리케이션에서 경로를 탐색할 때는, 최단 경로나 최소 환승 등 하나의 목적에도 여러 가지 방법이 있습니다. 이처럼 그래프의 모든 정점 탐색 방법에도 여러 가지가 있습니다. 그중에서 가장 대표적인 두 가지 방법, BFS와 DFS를 소개합니다. 이 둘은 데이터를 탐색하는 순서만 다를 뿐, 모든 자료를 하나씩 확인해 본다는 점은 같습니다.
다음의 예시를 통해 BFS와 DFS의 특징을 학습해 봅시다.
BFS(Breadth-First Search)
한국에서 미국으로 가는 비행기를 예약하려고 합니다. 비행편에 따라 직항과 경유가 있습니다. 만약 경유하게 된다면, 해당 항공사가 필요로 하는 공항에 잠시 머물렀다가 가기도 합니다. 경유하는 시간은 비행편마다 다르고, 경유지도 다릅니다. 이렇게 다양한 여정 중에서, 최단 경로를 알아내려면 어떻게 해야 할까요?
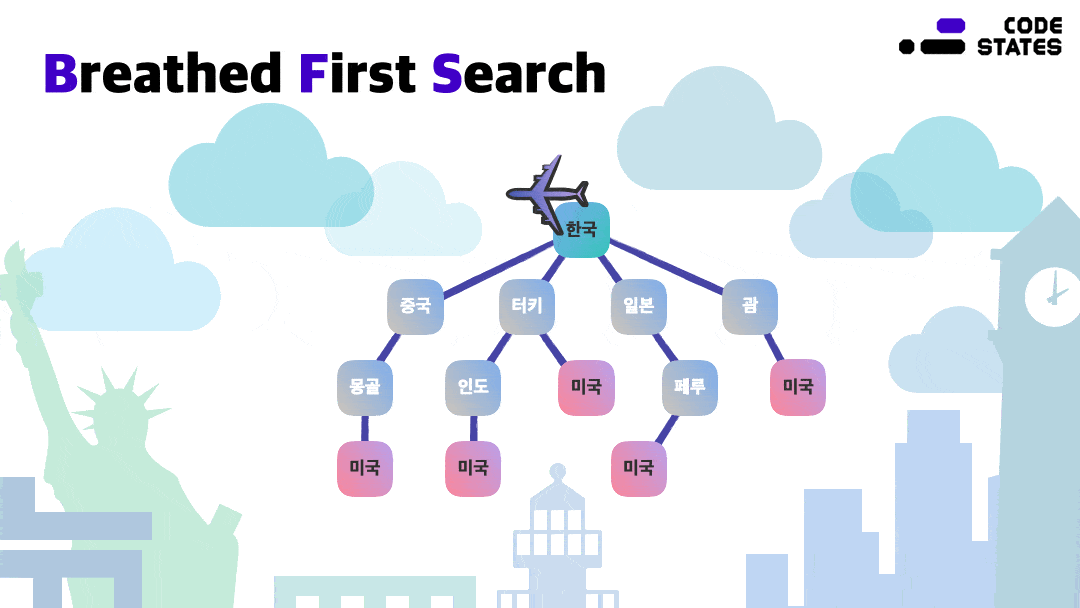
한국을 기준으로 미국까지 가는 방법을 가까운 정점부터 탐색합니다. 그리고 더는 탐색할 정점이 없을 때, 그다음 떨어져 있는 정점을 순서대로 방문합니다. 직항이라면 한국과 미국 사이에 어떠한 경유지도 없기 때문에 제일 가까운 정점에 미국이 있습니다.
경유지가 있다면 직항보다 거리가 멀다는 사실을 확인할 수 있습니다. 이렇게, 너비를 먼저 탐색하는 방법을 Breadth-First Search, 너비 우선 탐색이라고 합니다. 주로 두 정점 사이의 최단 경로를 찾을 때 사용합니다. 만약, 경로를 하나씩 전부 방문한다면, 최악의 경우에는 모든 경로를 다 살펴보아야 합니다.
Q) 왜 최단 경로를 찾을 때 BFS 방식을 사용할까요?
한 경로를 끝까지 모두 다 탐색하는 처음 발견한 답이 최단 거리가 아닐 수 있지만, BFS는 현재 있는 노드에서 가까운 곳부터 탐색하므로 경로를 탐색하는 도중 가장 먼저 발견한 해답이 최단거리라는 보장이 되기 때문입니다.
DFS(Depth-First Search)
그렇다면, 한국에서 출발하는 항공기의 모든 경로 중에 미국에 도착하는 여정을 알아내고 싶을 때는 어떻게 해야 할까요?
비행기 티켓이 없다면 어떤 비행기가 미국으로 가는 것인지 알 수 없습니다. 이때 비행기를 타고 여러 나라를 방문하면서, 마지막에 미국에 도착하는 경로를 찾아야 합니다.
DFS는 하나의 경로를 끝까지 탐색한 후, 미국 도착이 아니라면 다음 경로로 넘어가 탐색합니다. 하나의 노선을 끝까지 들어가서 확인하고 다음으로 넘어가기 때문에, 운이 좋다면 단 몇 번 만에 경로를 찾을 수 있습니다. 또 미국으로 가는 길이 아님을 미리 체크할 수 있다면, 바로 그 순간 다음 탐색으로 넘어갈 수 있습니다.
이렇게, 깊이를 먼저 탐색하는 방법을 Depth-First Search, 깊이 우선 탐색이라고 합니다. 한 정점에서 시작해서 다음 경로로 넘어가기 전에 해당 경로를 완벽하게 탐색할 때 사용합니다. BFS보다 탐색 시간은 조금 오래 걸릴지라도 모든 노드를 완전히 탐색할 수 있습니다.
DFS와 BFS는 모든 정점을 한 번만 방문한다는 공통점을 가지고 있지만, 사용할 때의 장단점은 분명하기 때문에 해당하는 상황에 맞는 탐색 기법을 사용해야 합니다.

