BST의 범위 합

문제설명

root이진 검색 트리의 노드와 두 개의 정수 low및 가 주어지면 값이 포함된 범위 에 있는 모든 노드의 값의 합을high 반환합니다 .[low, high]

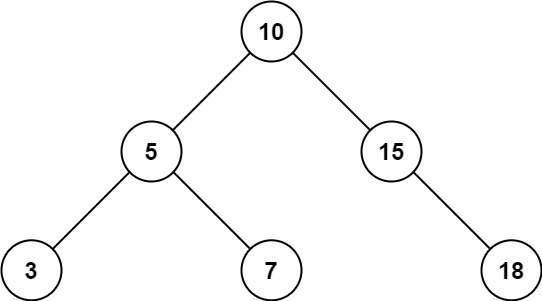
입력: root = [10,5,15,3,7,null,18], low = 7, high = 15
출력: 32

설명: 노드 7, 10 및 15는 [7, 15] 범위에 있습니다. 7 + 10 + 15 = 32.

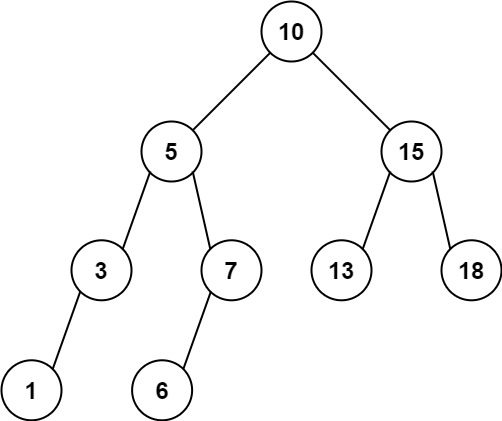
입력: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
출력: 23
설명: 노드 6, 7, 10은 [ 범위에 있습니다. 6, 10]. 6 + 7 + 10 = 23.

class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        if not root:
            return 0
        
        if root.val < low:
            return self.rangeSumBST(root.right, low, high)
        elif root.val > high:
            return self.rangeSumBST(root.left, low, high)
        else:
            return root.val + self.rangeSumBST(root.left, low, high) + self.rangeSumBST(root.right, low, high)

이진 검색 트리의 특성:

왼쪽 서브트리에는 현재 노드의 값보다 작은 값이, 오른쪽 서브트리에는 현재 노드의 값보다 큰 값이 저장됩니다.
이진 검색 트리에서는 검색, 삽입, 삭제 등의 기본 연산이 효율적으로 수행될 수 있습니다.
시간 복잡도는 균형 상태일 때 O(logN)입니다.
이진 검색 트리는 정렬된 데이터를 효율적으로 저장하고 관리할 수 있어, 다양한 알고리즘에서 활용됩니다.
이진 검색 트리의 균형을 유지하는 것이 중요하며, 이를 위해 AVL 트리, 레드-블랙 트리 등의 자가 균형 이진 검색 트리가 사용됩니다.

<내 코드의 흐름>

1. 이 메서드는 이진 검색 트리의 루트 노드(root), 범위의 최소값(low), 범위의 최대값(high)을 입력으로 받아 범위 내의 모든 노드 값의 합을 반환합니다.

2. 현재 노드의 값이 low보다 작다면, 오른쪽 서브트리만 탐색하면 됩니다. 따라서 rangeSumBST 메서드를 오른쪽 자식 노드에 대해 재귀적으로 호출합니다.

3. 현재 노드의 값이 high보다 크다면, 왼쪽 서브트리만 탐색하면 됩니다.
   따라서 rangeSumBST 메서드를 왼쪽 자식 노드에 대해 재귀적으로 호출합니다.

4. 현재 노드의 값이 low와 high 사이에 있다면, 현재 노드의 값을 더하고 왼쪽, 오른쪽 서브트리를 모두 탐색해야 합니다. 따라서 현재 노드의 값을 더하고, 왼쪽 자식 노드와 오른쪽 자식 노드에 대해 rangeSumBST 메서드를 재귀적으로 호출합니다.