2.1 기초수학 스터디노트

진수변환

• binary : bin() 2진수
• octal : oct() 8진수
• hexadecimal : hex() 16진수

■ 문제풀이

dNum = 30

print('2진수 : {}'.format(bin(dNum)))
print('8진수 : {}'.format(oct(dNum)))
print('16진수 : {}'.format(hex(dNum)))

###이때 반환값은 type은 str로 나옴###


#(또다른 방법1) format 함수 사용
print('2진수 : {}'.format(format(dNum, '#b'))) 
# 0b : 2진수라는 것을 알려주는 것

print('8진수 : {}'.format(format(dNum, '#o')))  # 0o
print('16진수 : {}'.format(format(dNum, '#x')))  #0x

[Output]
2진수 : 0b11110
8진수 : 0o36
16진수 : 0x1e

.

# #을 없애면 출력값 앞에 각 어떤 진수임을 표시하는 기호가 나오지 않음
print('2진수 : {}'.format(format(dNum, 'b')))
print('8진수 : {}'.format(format(dNum, 'o')))
print('16진수 : {}'.format(format(dNum, 'x')))

[Output]
2진수 : 11110
8진수 : 36
16진수 : 1e

.

#(또다른 방법2)
print('{0:#b}, {0:#o}, {0:#x}'.format(dNum, dNum, dNum))
print('{0:#b}, {0:#o}, {0:#x}'.format(dNum)) #위와 동일

[Output]
0b11110, 0o36, 0x1e

.

#10진수로 바로 바꾸기
print('2진수(0b11110) ->  10진수({})'.format(int('0b11110', 2))) #[0]은 값, [1]은 형태
print('8진수(0o36) ->  10진수({})'.format(int('0o36', 8)))
print('16진수(0x1e) ->  10진수({})'.format(int('0x1e', 16)))

[Output]
2진수(0b11110) -> 10진수(30)
8진수(0o36) -> 10진수(30)
16진수(0x1e) -> 10진수(30)

등차수열 / 등비수열

■ 문제풀이
-공식없이 사용한 풀이

inputN1 = int(input('a1 입력 : '))
inputD = int(input('공차 입력 : '))
inputN = int(input('n 입력 : '))

valueN = 0; n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값 : {}'.format(n, valueN))
        n += 1
        continue

    valueN += inputD
    print('{}번째 항의 값 : {}'.format(n, valueN))
    n += 1

print('{}번째 항의 값 : {}'.format(inputN, valueN))

• 등차수열 공식활용
  ※ 등차수열 공식 : an = a1 + (n-1)d
  ※ 등차수열의 합 공식 : sn = n(a1 + an) / 2

inputN1 = int(input('a1 입력 : '))
inputD = int(input('공차 입력 : '))
inputN = int(input('n 입력 : '))

valueN = 0; n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값 : {}'.format(n, valueN))
        n += 1
        continue

    valueN += inputD
    print('{}번째 항의 값 : {}'.format(n, valueN))
    n += 1

print('{}번째 항의 값 : {}'.format(inputN, valueN))

#등차수열 공식으로

inputN1 = int(input('a1 입력 : '))
inputD = int(input('공차 입력 : '))
inputN = int(input('n 입력 : '))

valueN = 0
#공식 : an = a1 + (n-1)d
valueN = inputN1 + (inputN - 1)*inputD
print('{}번째 항의 값 : {}'.format(n, valueN))

• 등비수열 공식활용
  ※ 등비수열 공식 : an = a1 r**(n - 1)
  ※ 등비수열의 합 공식 : sn = a1 (1 - r**n) / (1 - r)

계차수열 : 두 항의 차로 이루어진 또다른 수열

inputAN1 = int(input('a1 입력 :  '))
inputAN = int(input('an 입력 :  '))

inputBN1 = int(input('b1 입력 :  '))
inputBD = int(input('bn 입력 :  '))

valueAN = 0; valueBN = 0
n = 1

while n <= inputAN:
	if n == 1:
      valueAN = inputAN1
      valueBN = inputBN1
      print('an의 {}번째 항의 값 : {}'.format(n, valueAN))
      print('bn의 {}번째 항의 값 : {}'.format(n, valueBN))
      n += 1
      continue
	
   valueAN = valueAN + valueBN
   valueBN = valueBN + valueBD
   n += 1
   
print('an의 {}번째 항의 값 : {}'.format(inputAN, valueAN))
print('bn의 {}번째 항의 값 : {}'.format(inputAN, valueBN))

※ 계차 수열 공식
an = n**2 + n + 1

군수열 : 여러 개의 항을 묶었을 때 규칙성을 가지는 수열

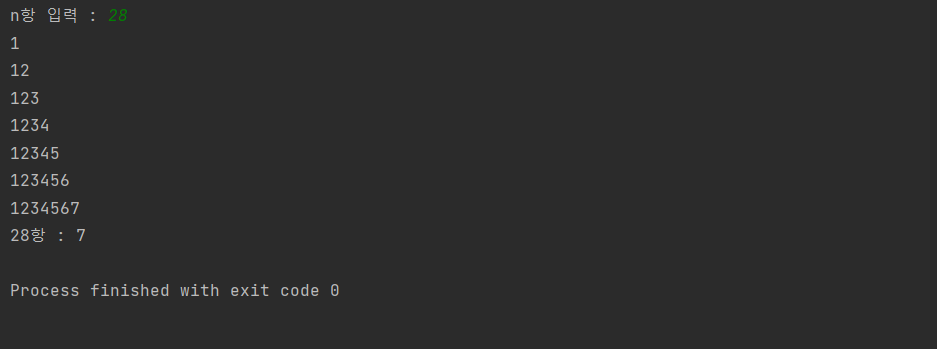
inputN = int(input('n항 입력 : '))

flag = True
n = 1; nCnt = 1; searchN = 0

while flag:
	for i in range(1, (n+1)):
    	print(f'{i}', end = '')
 
        nCnt += 1  #누적 항 갯수
        
        if nCnt > inputN:
        	searchN = i
            flag = False
            break #for 문을 빠져나옴
    print()        
    n += 1
    
print('{}항 : {}'.format(inputN, searchN))
    

[Output]

inputN = int(input('n항 입력 : '))

flag = True
n = 1; nCnt = 1; searchNC = 0; searchNP = 0

while flag:
	for i in range(1, (n+1)):
    	if i == n:
        	print('{}/{}, '.format(i, (n - i + 1)), end='')
        else:
        	print('{}/{}'.format(i, (n - i + 1)), end='')
        
        nCnt += 1
        
        if nCnt > inputN:
        	searchNC = i
            searchNP = n - i + 1
            flag = False
            break
            
   print()
   n += 1
   
print()
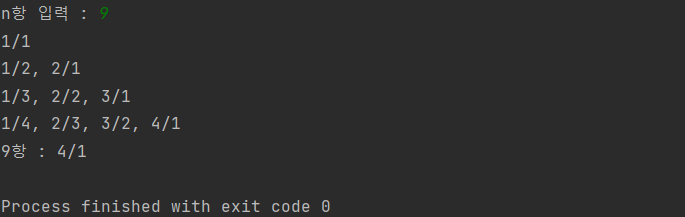
print('{}항 : {}/{}'.format(inputN, searchNC< searchNP))
            

[Output]

순열 : 일렬로 나열하는 경우의 수

numN = int(input('numN 입력 : '))
numR = int(input('numR 입력 : '))
result = 1

for n in range(numN, (numN - numR) , -1):
	print('n : {}'.format(n))
    result = result * n
    
print('result: {}'.format(result))

◆ 추가개념 : 원 순열(시작과 끝의 구분이 없는 순열)
---> n! / n or (n-1)!

조합 : 순서에 관계없이 n개 중 r개를 선택하는 것

numN = int(input('numN 입력 : '))
numR = int(input('numR 입력 : '))
resultP = 1; resultR = 1; resultC = 1

for n in range(numN, (numN - numR), -1):
	print('n : {}'.format(n))
    resultP = resultP * n
    
print('resultP : {}'.format(reusltP))

for n in range(numR, 0, -1):
	print('n : {}'.format(n))
    resultR = resultR * n

print('resultR : {}'.format(resultR))

resultC = int(resultP / resultR)
print('resultC : {}.format(resultC))

확률 : 모든 사건에서 특정한 사건이 일어날 수 있는 수

#7장 중 꽝 2개와 선물 1개를 뽑는 확률을 출력하자(꽝 전체 4개, 선물 3개)

#조합을 구하는 방법 : nPr / r!

def proFun():  #확률 구하는 방법을 함수로 정리해서 바로 처리할 수 있다.
  numN = int(input('numN 입력 : '))
  numR = int(input('numR 입력 : '))

  resultP = 1; resultR = 1; resultC = 1


  for n in range(numN, (numN - numR), -1):  nPr 구하기
      resultP *= n
  print('resultP: {}'.format(resultP))


  for n in range(numR, 0, -1): #r! 구하기
      resultR *= n
  print('resultR: {}'.format(resultR))

  resultC = int(resultP / resultR)
  
  return resultC