🔎 퍼셉트론 perceptron (인공뉴런)
-
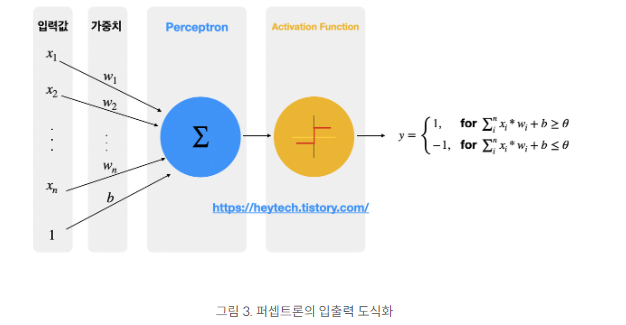
인지한 정보를 활용해 뉴런처럼 작동하는 방법으로 다수의 입력을 받아 하나의 신호로 출력한다.
-
TLU(threshold logic unit)라는 조금 다른 형태의 인공뉴런을 기반으로 하며 TLU는 입력의 가중치 합을 계산하고, 계산된 합에 계단 함수를 적용해 그 결과를 출력한다.
-
이때 각각 입력 신호에 가중치를 부여하는데, weight가 클 수록 중요한 신호로 볼 수 있다. 기계학습은 weight 값을 정하는 작업을 한다.
-
이진분류 모델을 학습하기 위한 지도학습 기반의 알고리즘, 각 출력 뉴런의 결정 경계는 선형이므로 퍼셉트론도 (로지스틱 회귀 분류기 처럼) 복잡한 패턴을 학습하지 못한다.
-
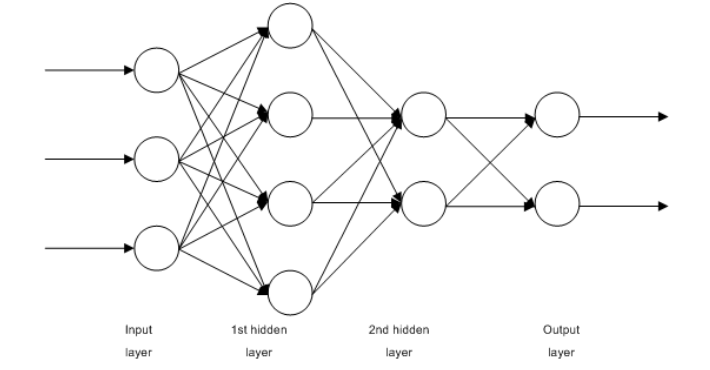
입력층, 출력층, 그 사이에 은닉층
-
단층 퍼셉트론, 다층 퍼셉트론
XOR 문제
: 논리 회로에 등장하는 개념으로 컴퓨터 0과 1을 입력해 하나의 값으로 출력하는 회로가 모여 만들어지는데, 이 때 회로를 게이트라고 한다.
[gate]
- AND : x1, x2 둘다 1일 때만 결과값이 1로 출력되는 게이트
- OR : x1, x2 둘 중 하나라도 1이면 결과값이 1로 출력되는 게이트
- XOR : x1, x2 둘 중 하나만 1일 때만 결과 값이 1로 출력되는 게이트
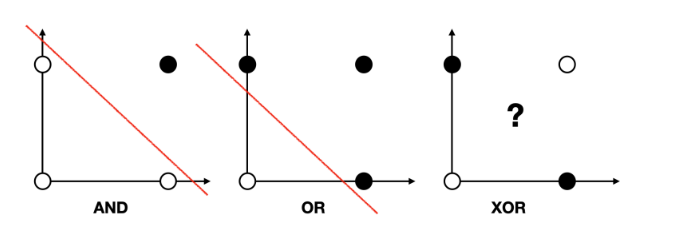
퍼셉트론 선형 모델로는 XOR 문제를 풀 수 없다.
➡️ XOR 문제를 해결하기 위한 방법으로 딥러닝, BackPropagation(역전파) 알고리즘을 사용한 다층 퍼셉트론.
- 다층 퍼셉트론을 이용하면 은닉층으로 두 개의 퍼셉트론을 한 번에 계산할 수 있게 되고 은닉층에서 공간을 외곡해 두 영역을 구분하는 직선을 구할 수 있게 되었다.
- 여러 개의 layer을 쌓은 후 학습해 실제 Y값과 예측 Y값의 차이를 구하고 다시 처음과정으로 돌아가 변주 재조정
🔎 역전파
- 다층 퍼셉트론 도식
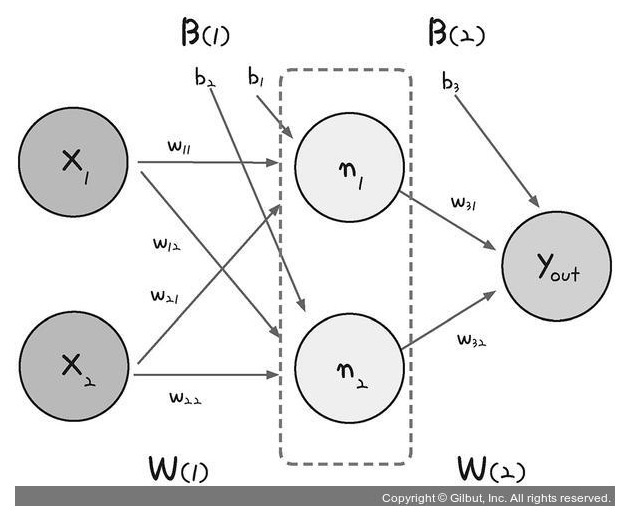
: 은닉층으로 퍼셉트론이 각각 가중치(w)와 바이어스(b) 값을 보내고, 은닉층에서 모인 값이 한 번 더 시그모이드 함수를 이용해 최종 값을 결과로 보낸다.
- 바이어스는 입력값이 0일 때 곱하면 항상 0이 출력되므로 이를 방지하기 위해 추가한 임의의 값
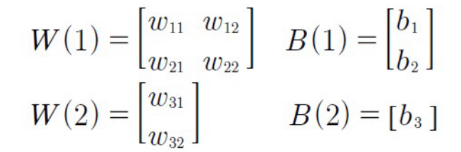
- 은닉층에 모이는 중간 정거장을 node라고 하며 n1, n2로 표시
- n1, n2 값은 각각 단일 퍼셉트론의 값과 같다.
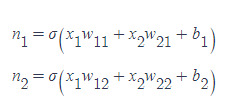
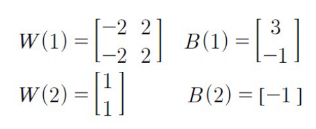
도식을 대입하면
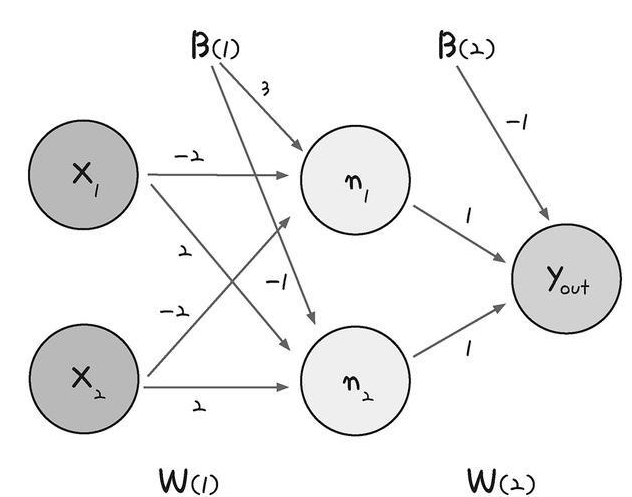
이렇게 된다.
각각 x1 x2 값을 입력하면

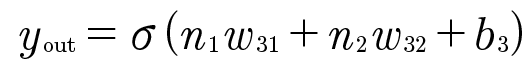
🔎 넘파이를 활용해 XOR 문제 풀기
import numpy as np
# 가중치와 편향
w11=np.array([-2,-2])
w12=np.array([2,2])
w2=np.array([1,1])
b1=3
b2=-1
b3=-1
# 퍼셉트론
def MLP(x,w,b):
y=np.sum(w*x)+b
if y <=0:
return 0
else:
return 1
# Negative AND(NAND): AND 게이트의 정반대 값을 출력
def NAND(x1,x2):
return MLP(np.array([x1,x2]),w11,b1)
# OR
def OR(x1,x2):
return MLP(np.array([x1,x2]),w12,b2)
# AND
def AND(x1,x2):
return MLP(np.array([x1,x2]),w2,b3)
# XOR
def XOR(x1,x2):
return AND(NAND(x1,x2), OR(x1,x2))
#최종값 출력
for x in [(0,0),(1,0),(0,1),(1,1)]:
y = XOR(x[0],x[1])
print(f'입력값: {x}, 출력값: {y}')
#입력값: (0, 0), 출력값: 0
#입력값: (1, 0), 출력값: 1
#입력값: (0, 1), 출력값: 1
#입력값: (1, 1), 출력값: 0
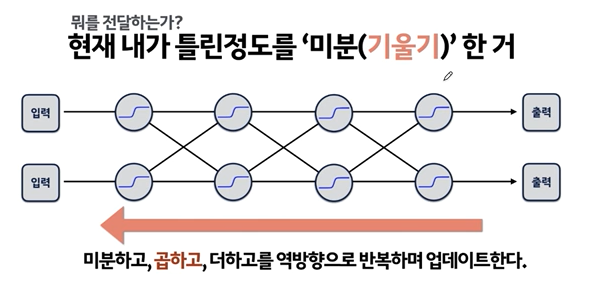
활성화함수
은닉층에서 자주 이용하는 활성함수
그래프 모양은 모두 다르지만 모두 특정 최솟값을 초과한 시점부터 출력값이 급격히 커지는 것
- 쌍곡 탄젠트함수
y=tanh(x) - 시그모이드 함수 `y=1/(1+e^-x)
- ReLU 함수 : y=0 (x<0일 때), y=x (x>=0일 때)
쌍곡 탄젠트 함수와 시그모이드는 값이 커지면 함수의 경사가 0에 가까워져서 학습이 더이상 진행되지 않는다는 단점이 있다.
계층의 종류
- 전결합층 : 노드가 많을 때 사용이 부적절해 은닉층 후반부나 출력층일 때 주로 사용한다
- 컨볼루션층 : 이미지를 다룰 때 주로 사용한다. 이미지를 계산할 때 이미지에 필터를 사용하는 효과와 같다 (필터란 이미지 특징을 강조하는 계산), 이미지에서 특칭을 추출한다
- 풀링 층 : 특정영역의 최대값을 취해 계산한다. 앞 층의 국소적인 노드에서 결정된 값을 자기 노드 값으로 취합해 작은 변화여도 같은 값으로 반환한다.
- 다른 타입의 층 조합 : 다양한 특성을 지닌 층을 조합해 처리 성능을 향상시킨다.
