[스터디] Heap

📍트리 구조

🔎 트리 구조 정의

한 노드에서 시작해서 다른 노드들을 순회하다가 자기 자신에게 되돌아오는 순환이 없는 연결 그래프이다.

🔎 트리 구조 용어

• 루트 노드(root node, 뿌리 노드): 트리의 최상단 노드
• 부모 노드(parent node): 노드 A가 노드 B를 가리킬 때 A는 B의 부모 노드이다.
• 자식 노드(child node): 노드 A가 노드 B를 가리킬 때 B는 A의 자식 노드이다.
• 잎 노드(leaf node, 리프 노드 | terminal node, 말단 노드): 자식이 없는 노드
• 내부 노드(internal node): 잎 노드가 아닌 노드

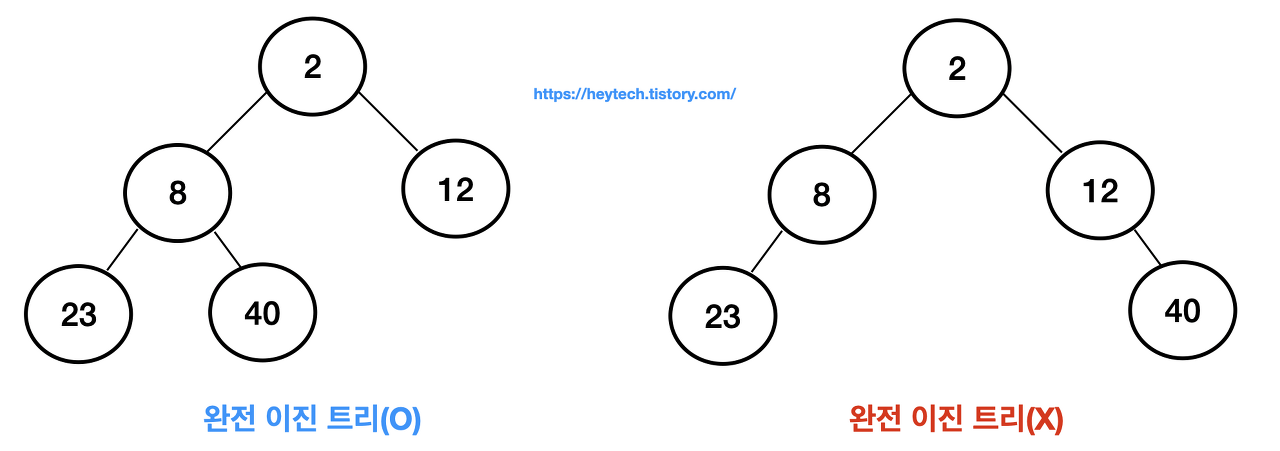
🔎 완전 이진 트리

이진 트리에 노드를 삽입할 때 왼쪽부터 차례대로 삽입하는 트리이다. 각 노드의 자식 노드가 반드시 2개인 트리이다.

📍Heap

🔎 Heap 정의

최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된, 완전이진트리를 기본으로 한 자료구조이다.

🔎 Heap 특징

• 힙 속성을 만족한다.
  • 힙 속성: A가 B의 부모노드라면, A의 키 값과 B의 키 값 사이에는 대소관계 성립한다.
• 키 값의 대소관계는 부모 노드와 자식 노드 사이에서만 성립한다.
• 형제 노드 사이에서는 대소관계가 성립하지 않는다.
• 우선순위 큐와 같이 최댓값 또는 최솟값을 빠르게 찾아야하는 알고리즘 등에 활용된다.

🔎 이진 Heap

• 힙 중에서 가장 널리 쓰이는 형태 중 하나로 이진 트리 형태인 힙이다.
• 이진 힙은 완전 이진 트리라는 조건을 만족해야 한다.

🔎 Heap 종류

• 최대 힙: 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 힙
• 최소 힙: 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작은 힙

🔎 Heap 동작

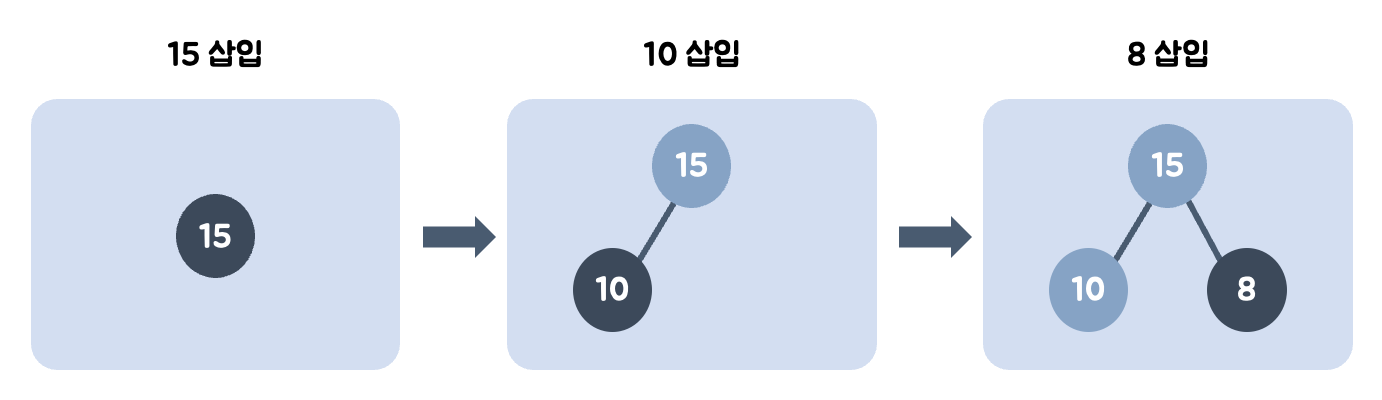
➕ 데이터 삽입

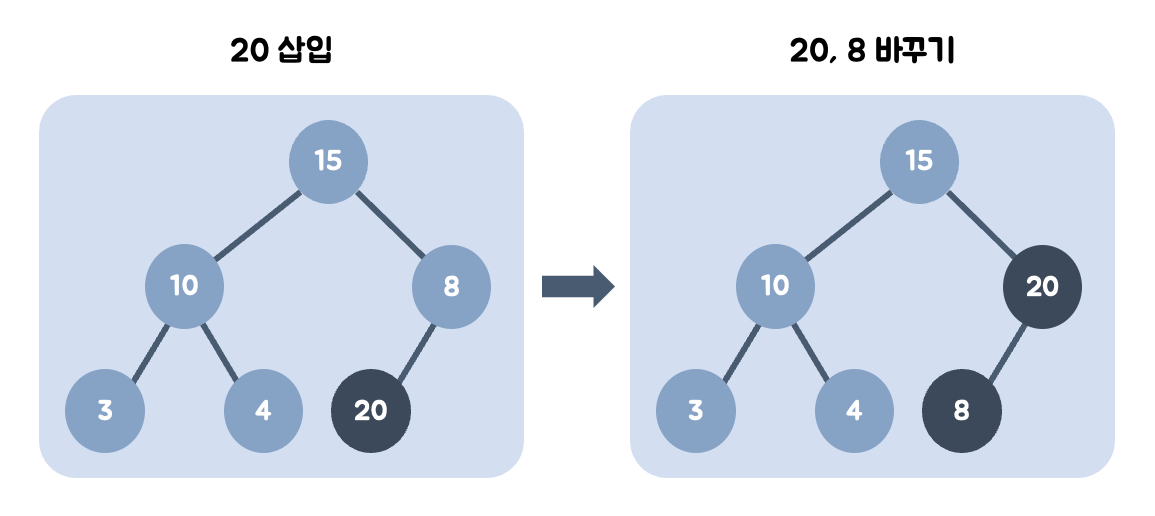
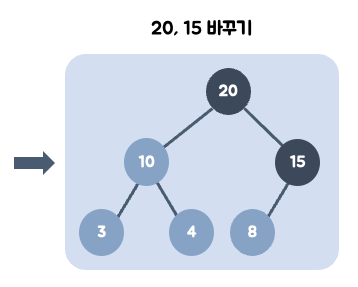
➕ 데이터 삽입(기존 힙에 있던 데이터보다 큰 경우)

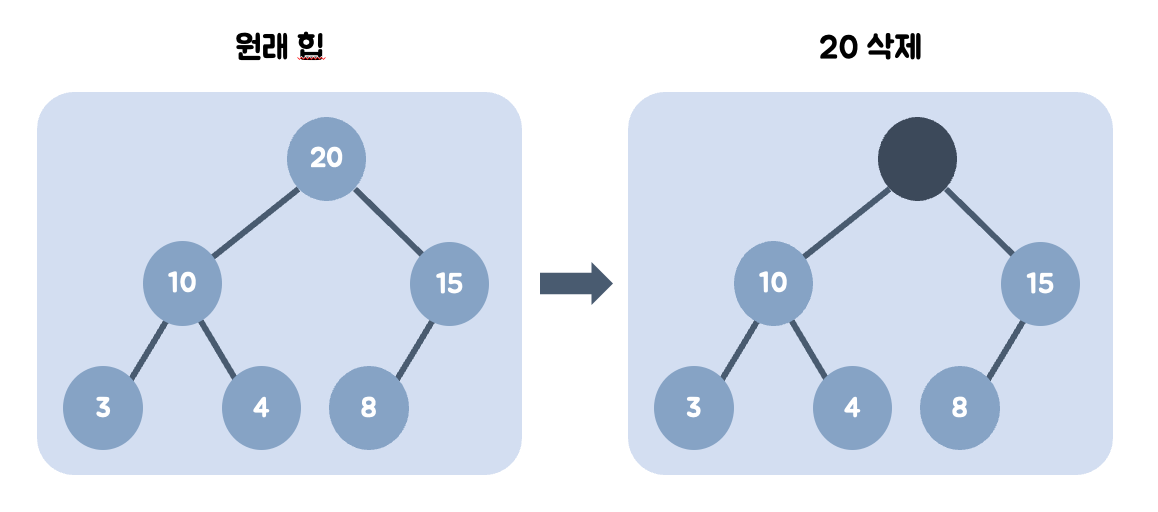
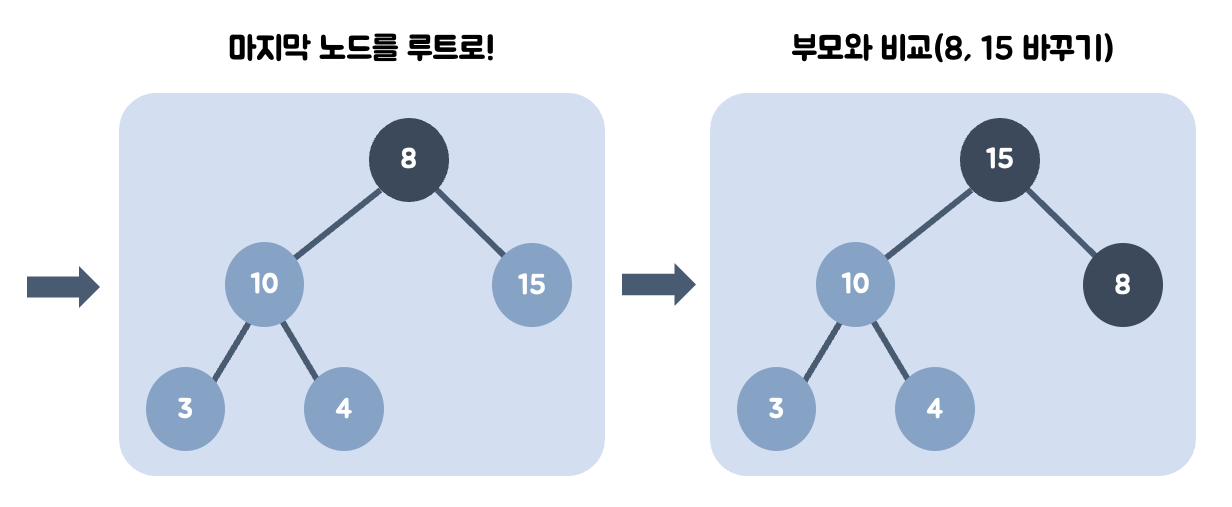
➕ 데이터 삭제

📍스터디 회고

• 더 알게된 내용
  힙을 사용하는 이유? 시간복잡도가 낮아 빠르게 처리 가능

• 추가로 공부하고자 하는 내용
  시간복잡도의 정확한 개념, 시간복잡도 계산 방식

📍공부한 곳

위키백과 - 힙, 트리구조, 완전이진트리
힙 설명 잘 되어있는 곳