[스터디] 트리 & 이진탐색트리

📍트리

🔎 트리 정의

• 하나의 노드에서 시작해 다른 정점들을 순회하다 자기 자신에게 돌아오는 순환이 없는 연결 그래프 (비선형 자료 구조)
• 일반적으로 대상정보의 각 항목들을 계층적으로 구조화 할때 사용

🔎 트리 용어

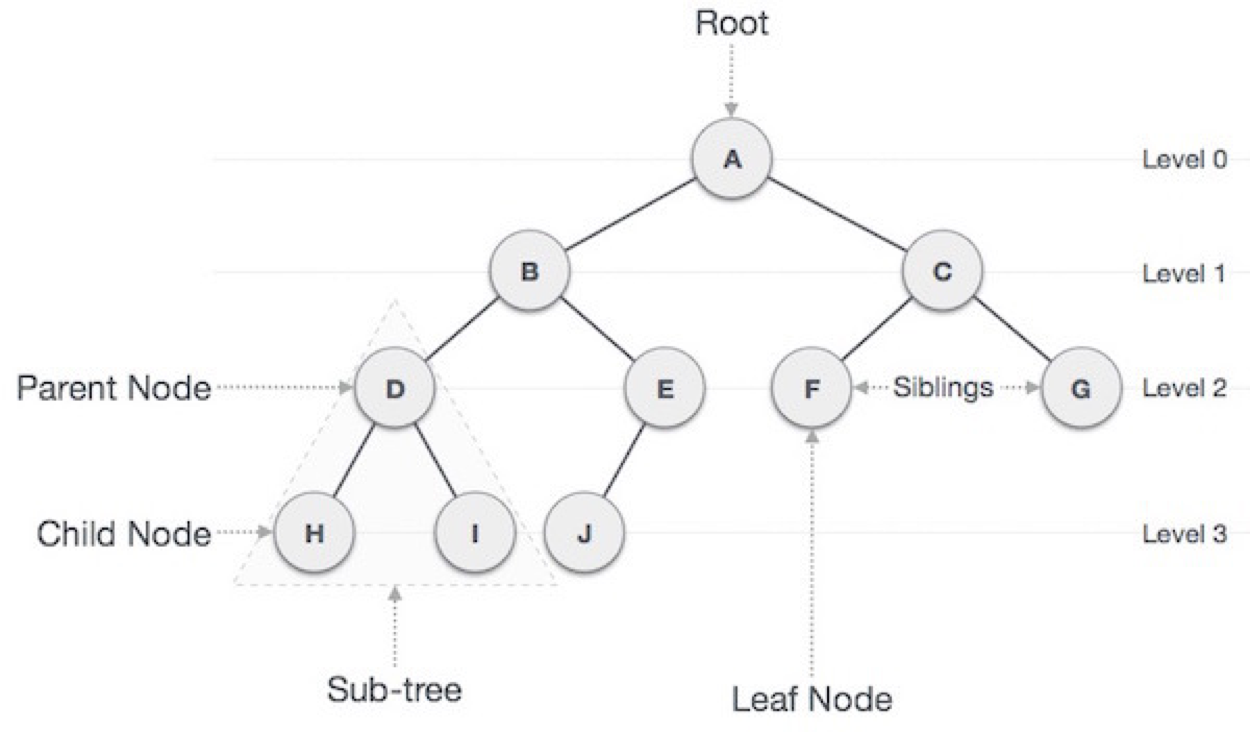
• Node : 트리 구조의 교점, 데이터를 가지고 있다.
• Root Node: 트리구조에서 가장 위에 있는 노드.
• Edge: 트리를 구성하기 위해 노드와 노드를 연결하는 선.
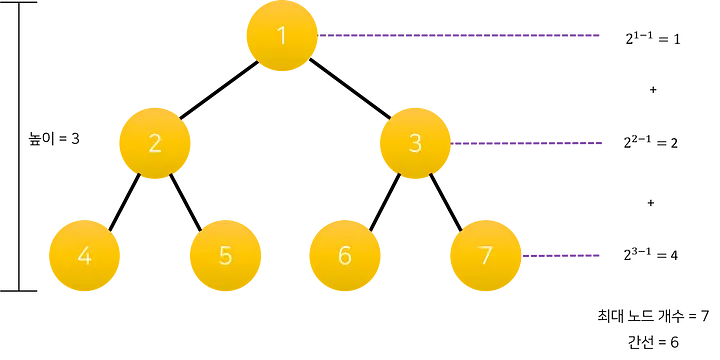
• height: 트리가 가지고 있는 최대 레벨.
• level: 트리의 특정 깊이를 가지는 노드의 집합 입니다.
• degree: 각 노드가 지닌 가지의 수. '차수'라고 한다.
• Leaf Node(Terminal Node): 하위에 다른 노드가 연결되어 있지 않은 노드.
• Internal Node: Leaf 노드를 제외한 중간에 위치한 노드.
• 부모 노드(parent node): 노드 A가 노드 B를 가리킬 때, A를 B의 부모 노드라고 한다.
• 자식 노드(child node): 노드 A가 노드 B를 가리킬 때, B를 A의 자식 노드라고 한다.

🔎 트리 특징

• 저장된 데이터를 더 효과적으로 탐색 하기 위해서 사용된다.
• 리스트와 다르게 데이터가 단순히 나열되는 구조가 아니라, 부모(parent)와 자식(child)의 계층적인 관계로 표현된다.
• 트리는 그래프(Graph)의 한 종류이며, 사이클이 없다.
• 트리에서 Root Node를 제외한 모든 노드는 단 하나의 부모노드를 가진다.

🔎 트리 사용

• 윈도우와 리눅스 같은 OS의 파일시스템 구조
• 대용량의 데이터를 계층적으로 저장할 때

🔎 트리 순회

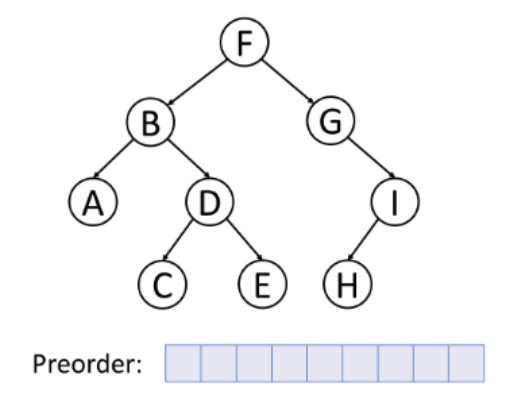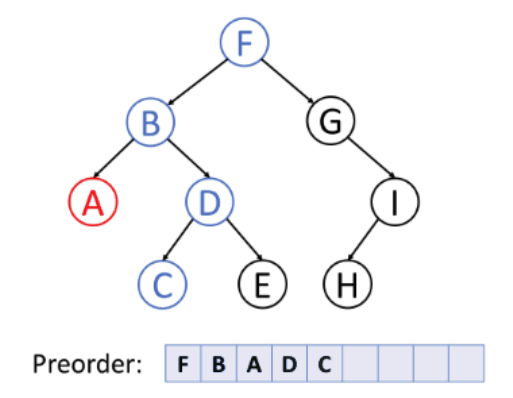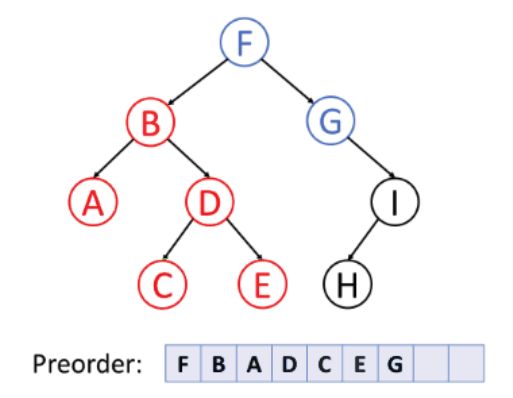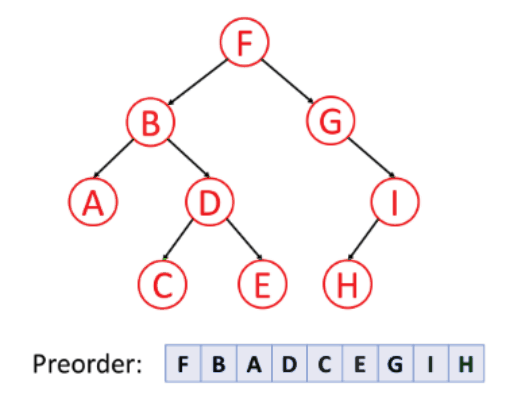
➕ 전위 순회 (Preorder)

• 루트노드 → 왼쪽 서브트리 → 오른쪽 서브트리
• 깊이 우선 순뢰라고 한다.
  

➕ 중위 순회 (Inorder)

• 왼쪽 서브 트리 → 노드 → 오른쪽 서브 트리
• 대칭 순회라고 한다.
  

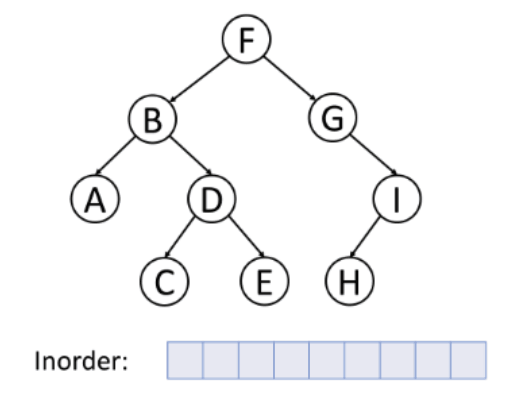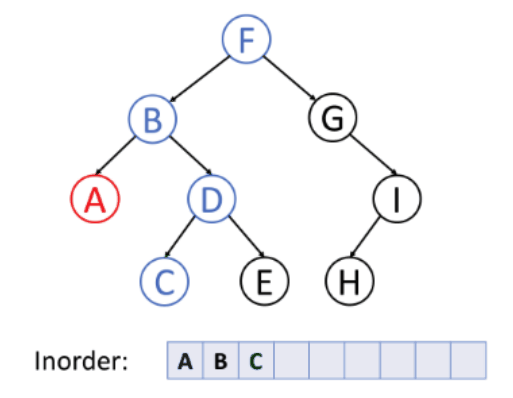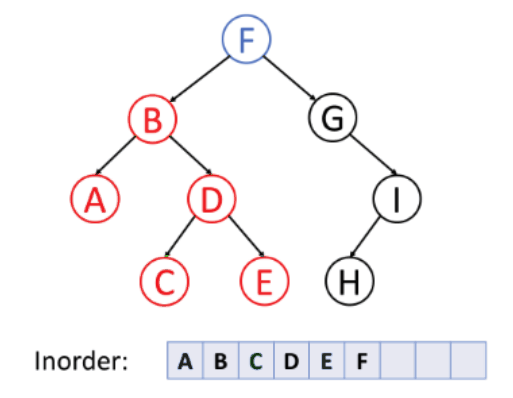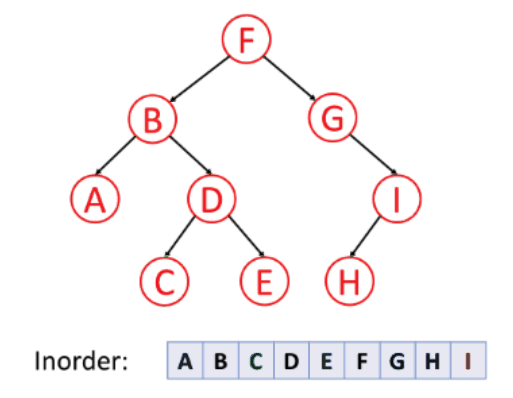
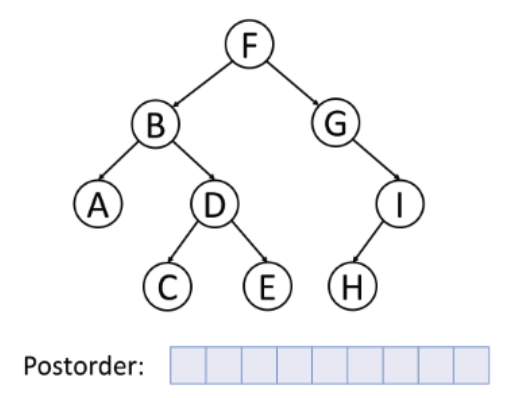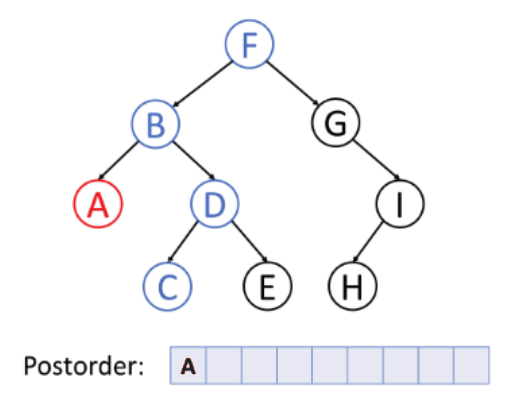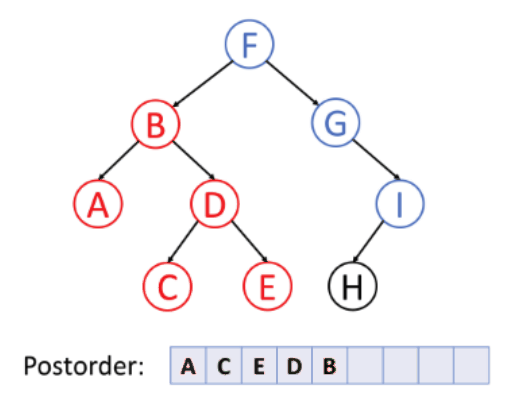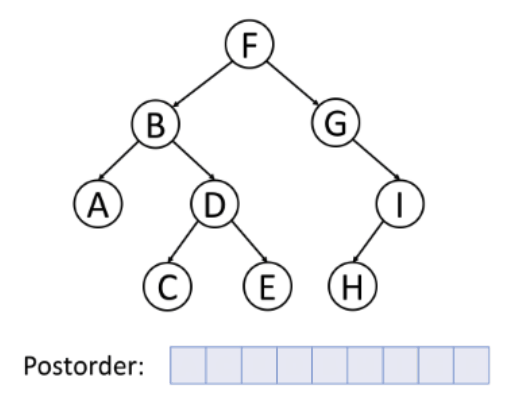
➕ 후위 순회 (Postorder)

• 왼쪽 서브 트리 → 오른쪽 서브 트리 → 노드
  

📍이진 트리

🔎 이진 트리 정의

• binary tree
• 모든 노드가 2개의 서브 트리를 가지고 있는 트리
• 서브 트리 또한 모두 이진 트리여야 하기 때문에 순환적으로 정의

🔎 이진 트리 특징

• 0~2개의 자식 노드가 존재

• 모든 노드의 차수는 2 이하

• 서브 트리간의 순서가 존재해 왼쪽 서브 트리와 오른쪽 서브 트리는 구별

• 일반 트리와 이진 트리의 차이점

  분류	일반 트리	이진 트리
  자식 노드의 개수	제한 없음	2개 이하
  노드의 개수	1개 이상	없을 수도 있음
  서브 트리 간의 순서	존재하지 않음	존재

🔎 이진 트리 종류

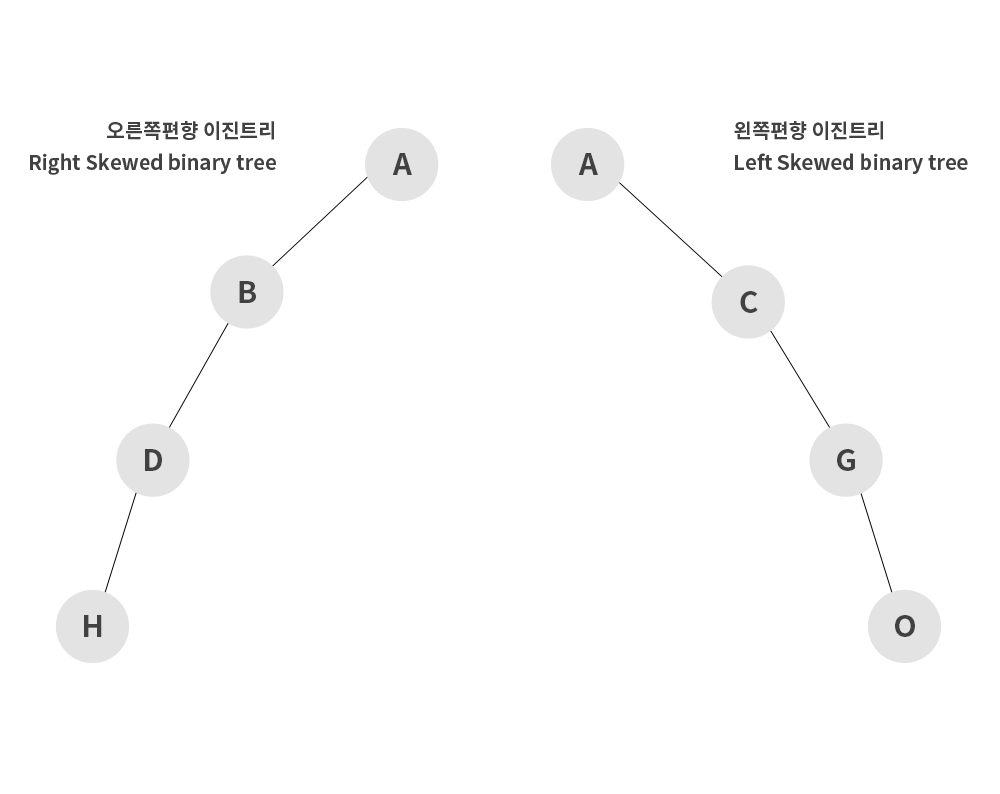
➕ 편향 이진 트리

• Skewed binary tree
• 하나의 차수로만 이루어져 있는 경우를 의미
• 배열(리스트)와 같은 선형 구조
• Leaf Node 탐색 시 모두 데이터를 전부 탐색해야 한다는 단점 -> 비효율적
• 높이 균형 트리: 위의 단점을 보완한 트리
  

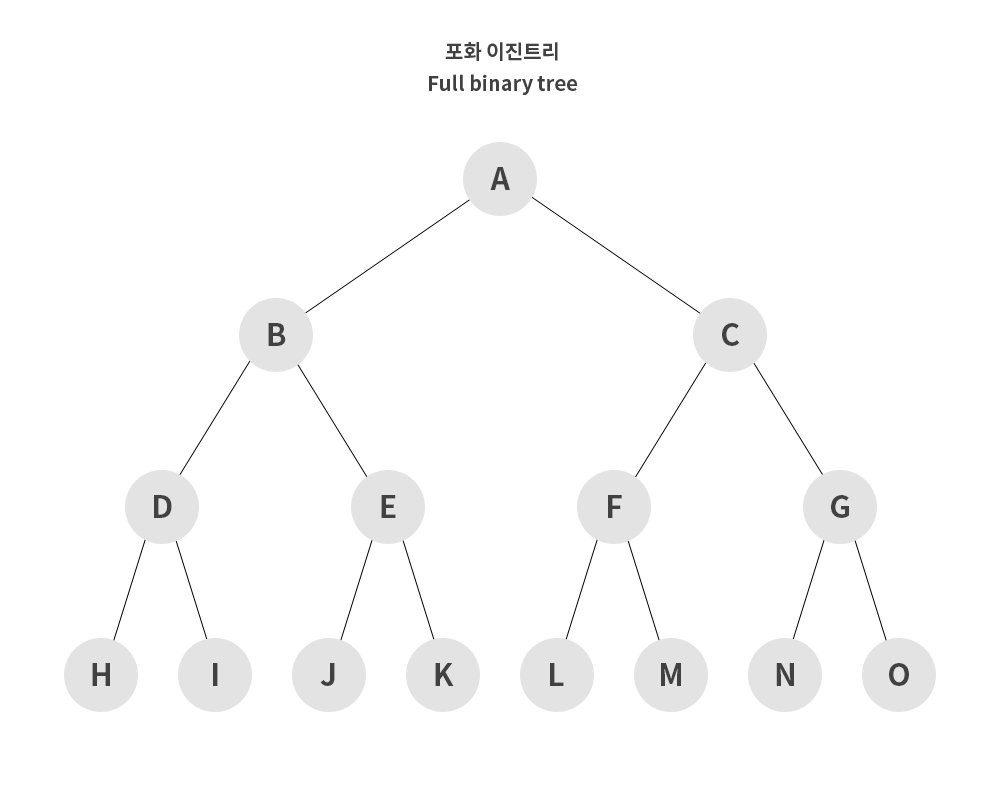
➕ 포화 이진 트리

• Full Binary Tree
• Leaf Node를 제외한 모든 노드의 차수가 두개로 이뤄진 경우
• 해당 차수에 몇 개의 노드가 존재하는지 바로 알 수 있다 -> 개수 파악이 용이
  

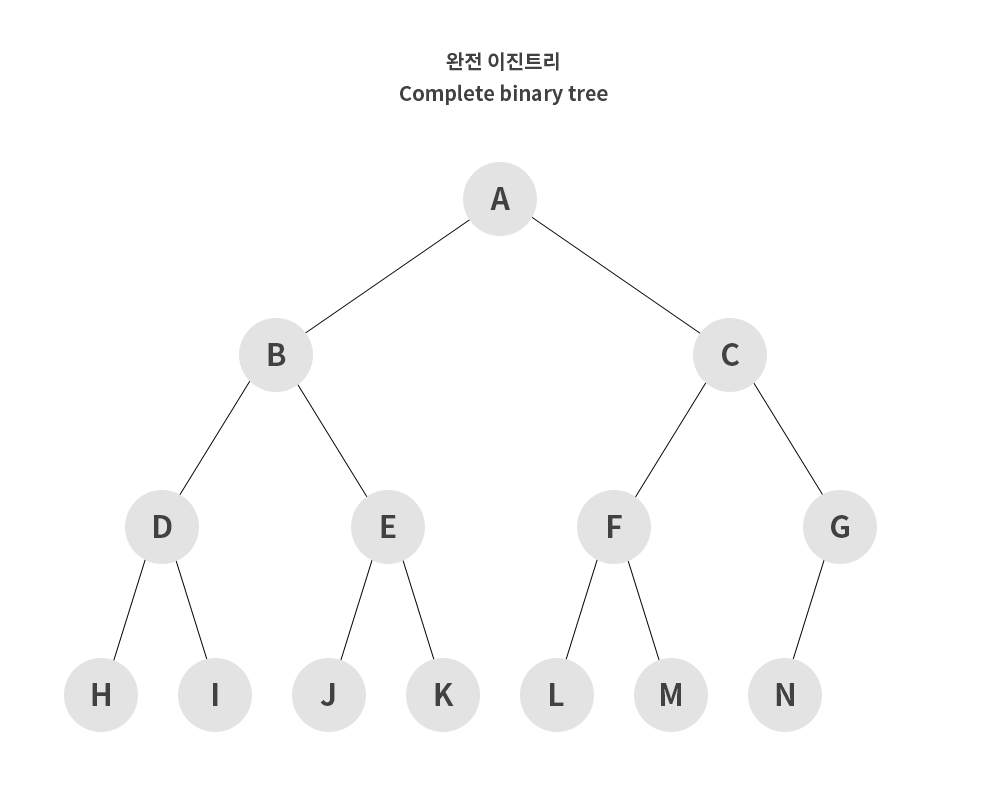
➕ 완전 이진 트리

• Complete Binary Tree
• 포화 이진 트리와 같은 개념으로 생성
• 모든 노드가 왼쪽부터 차근차근 생성
• Heap은 완전 이진 트리의 일종
  

📍이진 탐색 트리

🔎 이진 탐색 트리 정의

binary search tree, 탐색을 위한 이진 트리 기반의 자료 구조.

🔎 이진 탐색 트리 특징

• left node 에는 부모노드보다 작은 값이 저장됩니다.
• right node 에는 부모노드와 값이 같거나 큰 값이 저장됩니다.
• 모든 노드는 중복된 값을 가지지 않습니다.
• 이진 탐색 트리는 시간복잡도 O(log N), 리스트의 검색은 O(N). 따라서 검색하는 경우 이진탐색트리가 더 효율적이다.

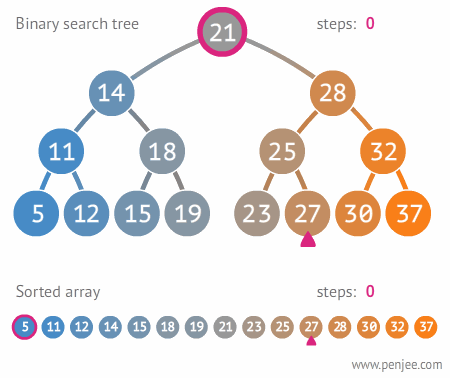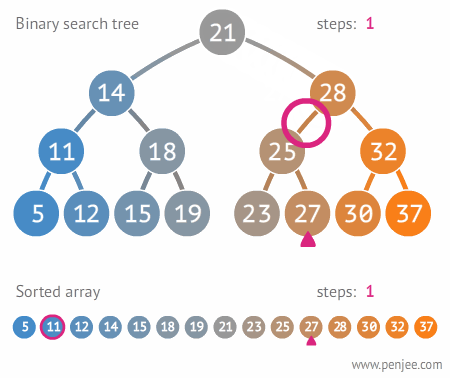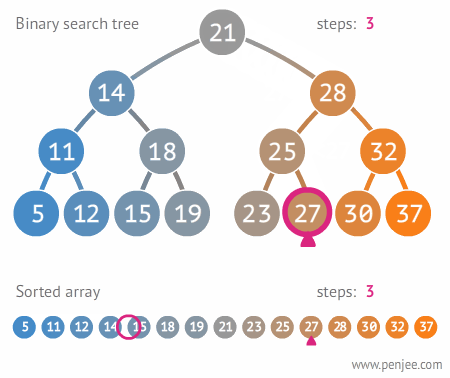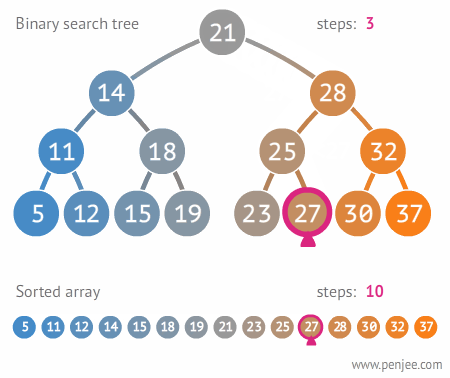
🔎 이진 탐색 트리 예시

이진 트리로 저장
[21, 28, 14, 32, 25, 18, 11, 30, 19, 15]

이진 탐색 트리 사용
원하는 값을 찾을 때까지 계속한다.
현재의 node값보다 찾고자하는 값이 크면 왼쪽, 작으면 오른쪽으로 움직인다.

📍스터디 회고

🔎 추가로 알게 된 내용

• 트리의 장점: 빠른 삽입과 삭제: O(log n)의 시간 복잡도

• 재귀적 특성이 있다. (BFS)
  -불균형 트리의 경우 검색 시간이 O(n) 까지 증가

• 트리의 크기가 커질 경우 많은 메모리를 요구한다.

• BFS: 층별 순회(level order)

  • 같은 레벨의 노드를 전부 탐색 후 다음 레벨의 노드 탐색

📍공부한 곳

https://velog.io/@taeha7b/datastructure-tree
https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC-Tree
https://medium.com/quantum-ant/%ED%8A%B8%EB%A6%AC-tree-cec69cfddb14