분할 정복 알고리즘
분할 정복 알고리즘(Divide and conquer algorithm)은 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이다.
대표적인 예로는 퀵 정렬이나 합병 정렬과 이진 탐색 등이 있다.
분할 정복 설계
1) Divide
원래 문제가 분할하여 비슷한 유형의 더 작은 하위 문제로 분할이 가능할 때 까지 나눈다.
2) Conquer
각 하위 문제를 재귀적으로 해결한다. 하위 문제의 규모가 나눌 수 없는 단위가 되면 탈출 조건을 설정하고 해결한다.
3) Combine
Conquer한 문제들을 통합하여 원래 문제의 답을 얻어 해결한다.
2630 - 색종이 만들기
문제

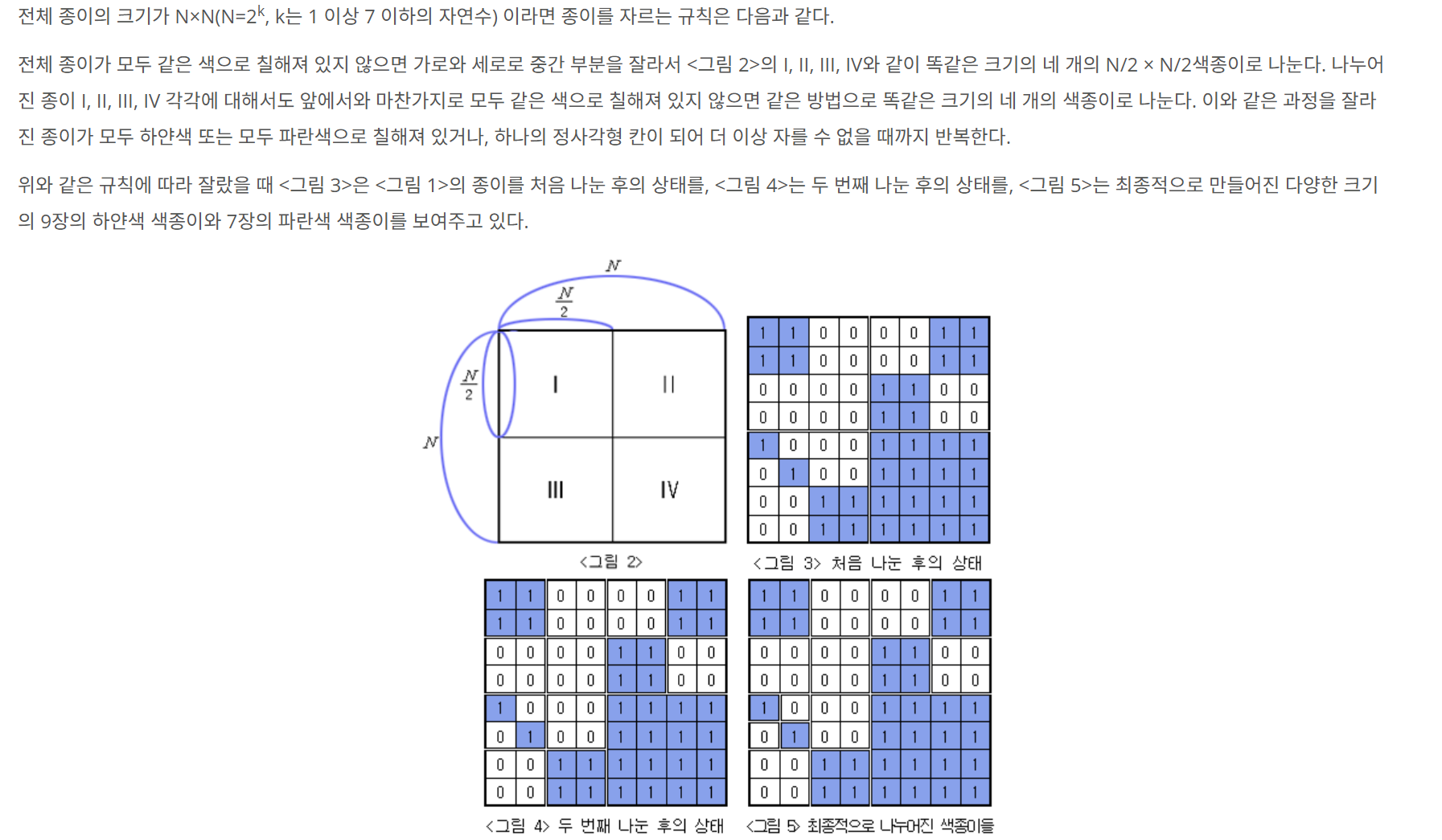
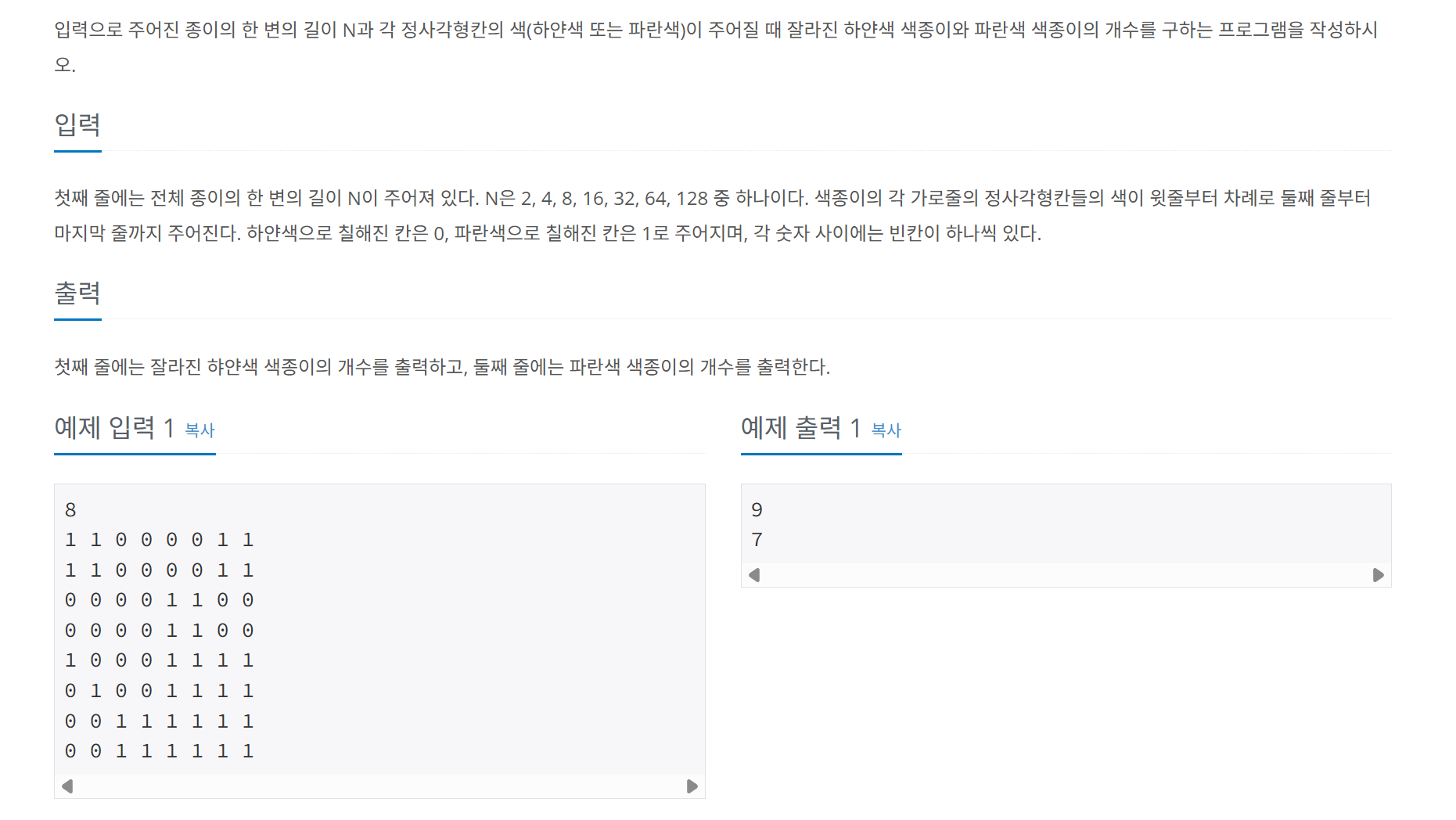
코드
#include <stdio.h>
int paper[128][128], zero, one;
int search(int x, int y, int n){
int count = 0;
for(int i=x; i<x+n; i++){
for(int j=y; j<y+n; j++){
if(paper[i][j]==1) count++;
}
}
if(count == n * n) one++;
else if(count == 0) zero++;
else{
search(x, y, n/2);
search(x, y+n/2, n/2);
search(x+n/2, y, n/2);
search(x+n/2, y+n/2, n/2);
}
}
int main(void){
int n;
scanf("%d", &n);
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
scanf("%d", &paper[i][j]);
}
}
search(0, 0, n);
printf("%d\n%d", zero, one);
}2차원 배열을 활용했고, 1개의 정사각형을 1, 2, 3, 4사분면으로 나누어 조건이 만족될때마다 count를 높여가며 재귀적으로 문제를 풀었다.
이때 count와 n을 비교한 값을 종료 조건으로 설정하고 n/2으로 절반씩 줄여나가는 방법을 사용했다.
같은 원리로 Z라는 문제를 접근했는데 시간 초과 문제가 생겼다.
1074 - Z
문제


코드
#include <stdio.h>
int count = 0; // 전역변수 초기화
int r, c;
int search(int x, int y, int n) {
if (n == 1) {
if (x == r && y == c) {
return 1; // 찾았을 때 1 반환
}
} else {
int half = n / 2;
// 1사분면
if (r < x + half && c < y + half) {
return search(x, y, half);
} else {
count += half * half;
}
// 2사분면
if (r < x + half && c >= y + half) {
return search(x, y + half, half);
} else {
count += half * half;
}
// 3사분면
if (r >= x + half && c < y + half) {
return search(x + half, y, half);
} else {
count += half * half;
}
// 4사분면
if (r >= x + half && c >= y + half) {
return search(x + half, y + half, half);
} else {
count += half * half;
}
return 0;
}
}
int main() {
int n;
scanf("%d %d %d", &n, &r, &c);
int size = 1 << n; // 2^n 계산하기 위한 비트연산
search(0, 0, size); // 좌표 0, 0 부터 탐색
printf("%d\n", count);
return 0;
}처음엔 색종이 만들기 문제와 같이 모든 사분면을 조사해보며 함수가 호출 될때마다 count를 증가시키는 방식을 사용했다.
예제까지는 잘 실행됐지만 2의 지수꼴로 조사해야하는 범위가 늘어날수록 시간이 기하 급수적으로 늘어나다보니 시간 초과 문제가 생겼다.
그래서 이를 해결하고자 각 사분면을 하나하나 조사하는게 아닌 count+=n*n을 통해 시간을 엄청나게 줄일 수 있었다.
이렇게 분할 정복에다가 조사하지 않아도 되는 부분을 n*n과 같은 방법으로 넘기는 방법까지 더해지니 2의 지수꼴과 같이 규모가 커짐에 따라 얼마나 크게 실행 속도의 차이를 만들어 내는지 느낄 수 있었다.
이런 알고리즘과 자료구조를 기반으로 효율적으로 구현한 코드 하나하나가 적은 비용으로 효과적으로 운영할 수 있는 서비스의 기반이 되는 것이다.
시프트 연산자(<< / >>)를 활용한 지수 계산
시프트 연산은 좌항에 있는 피연산자를 우항에 있는 수만큼 비트 자리 이동하는 연산을 수행한다.
<< 는 왼쪽 쉬프트 연산자이고 >> 는 오른쪽 쉬프트 연산자이다.
왼쪽 쉬프트 연산을 하면 좌항에 있는 피연산자의 값이 우항에 있는 수만큼 왼쪽으로 자리 이동하고 빈 자리는 0으로 채우게 된다.
이 특성을 이용한다면 2의 거듭제곱을 Z 문제의 코드처럼 쉽게 구할 수 있다.
printf("%u\n", num1 << 1); // 2: 0000 0010: 2
printf("%u\n", num1 << 2); // 4: 0000 0100: 2^2
printf("%u\n", num1 << 3); // 8: 0000 1000: 2^3
printf("%u\n", num1 << 4); // 16: 0001 0000: 2^4
printf("%u\n", num1 << 5); // 32: 0010 0000: 2^5
printf("%u\n", num1 << 6); // 64: 0100 0000: 2^6
printf("%u\n", num1 << 7); // 128: 1000 0000: 2^7