[C] 선형 큐와 원형 큐의 구현과 사용

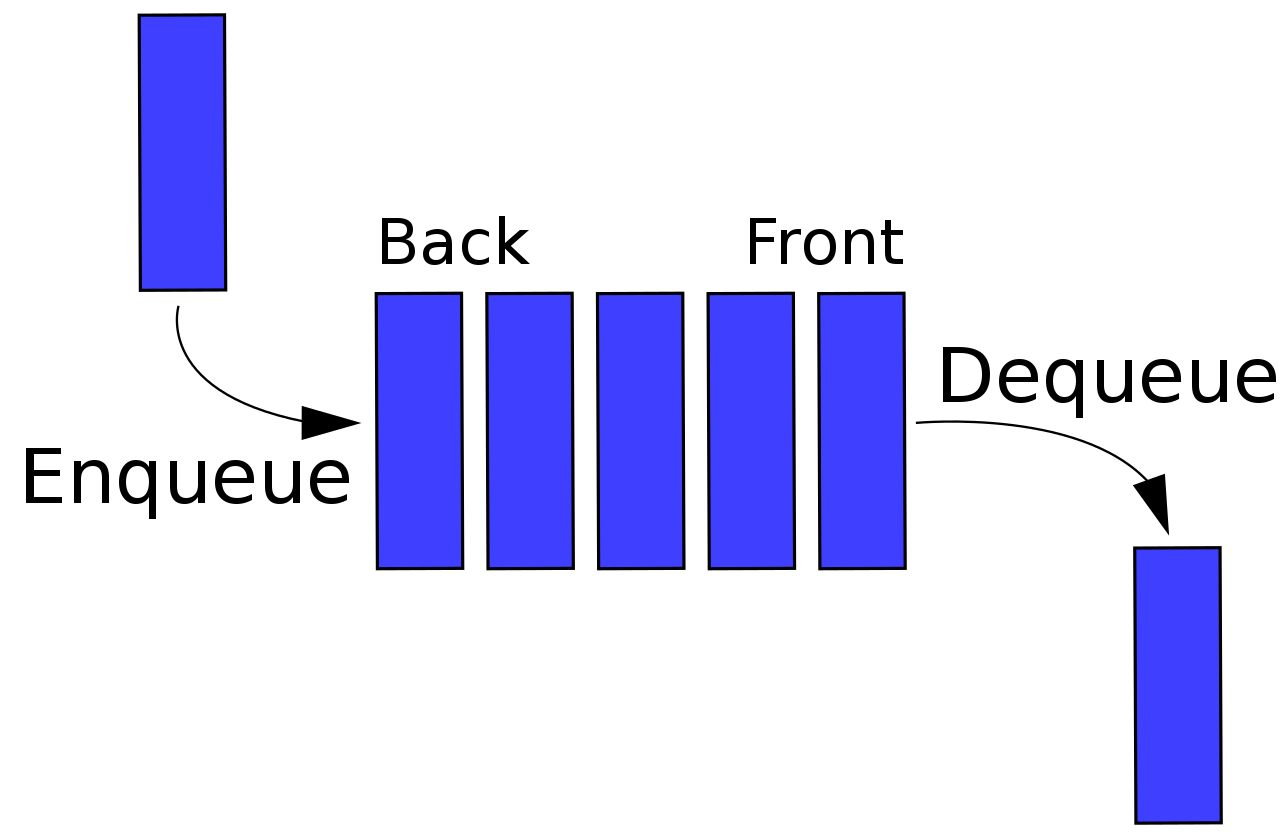
큐(Queue)란 ?

큐는 스택과 마찬가지로 데이터를 일시적으로 쌓아 놓은 자료구조이다.

가장 먼저 넣은 데이터를 가장 먼저 꺼내는 선입선출(FIFO)인 점이 스택과 다르다.

출처 : Vegpuff/Wikipedia

위 사진과 같은 형식의 자료구조인 큐에 데이터를 넣는 작업을 인큐(en-queue)라 하고, 데이터를 꺼내는 작업을 디큐(de-queue)라고 한다.

데이터를 꺼내는 쪽을 프론트(front)라 하고, 데이터를 넣는 쪽을 리어(rear)라고 한다.

인큐와 디큐를 진행할때 배열은 아래와 같이 변한다.

int que[10] = {1, 2, 3, 4, 0, 0, 0, 0, 0};

-> 인큐(5)

-> {1, 2, 3, 4, 5, 0, 0, 0, 0}

-> 디큐  

-> (1이 빠져나온다)

-> {0, 2, 3, 4, 0, 0, 0, 0, 0}

이와 같은 선형 큐는 사용할 수록 앞에 남는 사용할 수 없는 남는 공간이 생기기에 비효율적이다.

보완하기 위한 방법은 두 가지로 나뉜다.

1. 디큐시에 모든 요소를 한 칸씩 앞으로 당기기

2. 원형 큐를 사용하기

아래에서 이 두 가지 모두 다뤄보겠다.

큐(Queue) 구현하기

이 코드는 선형 큐의 단점을 없애기 위해 디큐시에 모든 요소를 한 칸씩 앞으로 당기는 기능을 추가한 코드이다.

#include <stdio.h>
#include <stdlib.h>

typedef struct{
  int max;
  int num;
  int *que;
}ArrayIntQueue;

int Initialize(ArrayIntQueue *s, int max){
  s->num = 0;
  if((s->que = calloc(max, sizeof(int)))==NULL){
    s->max = 0;
    return -1; //배열 생성 실패
  }
  s->max = max;
  return 0;
}

int Enque(ArrayIntQueue *s, int x){
  if(s->num >= s->max-1) return -1;
  s->que[s->num++] = x;
  return 0;
}

int Deque(ArrayIntQueue *s, int *x){ //포인터를 써야 매개변수로 x값에 접근가능
  if(s->num <= 0) return -1;
  *x = s->que[0];
  for(int i=0; i<s->max-1; i++){ //마지막 요소에도 실행하면 배열밖의 이상한 값 불러옴
    s->que[i]=s->que[i+1];
  }
  s->que[s->max-1] = 0; //직접 초기화
  return 0;
}

int Size(const ArrayIntQueue *s){
  return s->num;
}

int Capacity(const ArrayIntQueue *s){
  return s->max;
}

void Print(const ArrayIntQueue *s){
  for(int i=0; i<s->max; i++) printf("%d\n", s->que[i]);
}

void Terminate(ArrayIntQueue *s){
  if(s->que != NULL) free(s->que); //배열을 삭제
  s->max = s->num = 0;
}


void main(){
  ArrayIntQueue s;
  int value;
  printf("생성할 배열의 크기 : ");
  scanf("%d", &value);
  if(Initialize(&s, value) == -1){
    puts("스택 생성 실패");
  }
  while(1){
    int menu, x; //사용자 선택 수 저장하는 menu와 입력값이나 출력값 저장하는 x
    printf("\n현재 데이터 수 : %d / %d \n", Size(&s), Capacity(&s));
    printf("(1)인큐 (2)디큐 (3)출력 (0)종료 : ");
    scanf("%d", &menu);

    if(menu == 0) break;
    switch(menu){
      case 1:
        printf("데이터 : ");
        scanf("%d", &x);
        if(Enque(&s, x) == -1) puts("인큐 실패");
      break;

      case 2:
        if(Deque(&s, &x) == -1) puts("디큐 실패");
        else printf("디큐 데이터는 %d\n", x);
        break;

      case 3:
        Print(&s);
        break;
    }
  }
  Terminate(&s);
}





---------------------------------------
실행 결과


생성할 배열의 크기 : 10

현재 데이터 수 : 0 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 1
데이터 : 1

현재 데이터 수 : 1 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 1
데이터 : 2

현재 데이터 수 : 2 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 1
데이터 : 3

현재 데이터 수 : 3 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 1
데이터 : 4

현재 데이터 수 : 4 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 1
데이터 : 5

현재 데이터 수 : 5 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 3
1
2
3
4
5
0
0
0
0
0

현재 데이터 수 : 5 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 2
디큐 데이터는 1

현재 데이터 수 : 5 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 3
2
3
4
5
0
0
0
0
0
0

현재 데이터 수 : 5 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 2
디큐 데이터는 2

현재 데이터 수 : 5 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 3
3
4
5
0
0
0
0
0
0
0

현재 데이터 수 : 5 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 

스택을 구현하면서 사용했던 코드를 응용하여 직접 큐를 구현해보았다.

코드를 짜면서 배열 밖의 메모리를 불러오는 문제가 생겨 배열의 마지막 요소는 직접 초기화하는 방법으로 해결하였다.

int Deque(ArrayIntQueue *s, int *x){ //포인터를 써야 매개변수로 x값에 접근가능
  if(s->num <= 0) return -1;
  *x = s->que[0];
  for(int i=0; i<s->max-1; i++){ //마지막 요소에도 실행하면 배열밖의 이상한 값 불러옴
    s->que[i]=s->que[i+1];
  }
  s->que[s->max-1] = 0; //직접 초기화
  return 0;
}

------------------------------------
현재 데이터 수 : 4 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 3
1
2
3
4
0
0
0
0
0
0

현재 데이터 수 : 4 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 2
디큐 데이터는 1

현재 데이터 수 : 4 / 10 
(1)인큐 (2)디큐 (3)출력 (0)종료 : 3
2
3
4
0
0
0
0
0
0
132385

이처럼 모든 요소를 앞 당기는 코드를 추가함으로써 비효율성을 없앨 수 있다.

하지만 이 코드는 처리의 복잡도가 O(n)이다.

아래에서 O(1)로도 구현할 수 있는 원형 큐에 대해 알아보자.

링 버퍼로 큐 만들기(원형 큐)

앞서 구현한 큐에서 배열 요소를 이동시키는 작업 때문에 처리의 복잡도가 O(n)이었다.

복잡도를 개선하고자 배열 요소를 앞쪽으로 옮기지 않는 큐를 구현해보려고 한다.

이를 위해 사용되는 자료구조는 링 버퍼(ring buffer)이다.

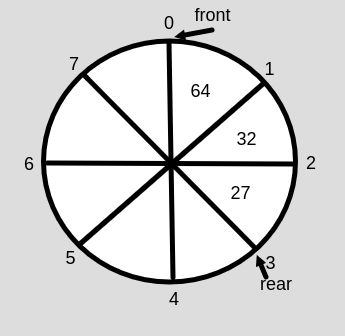
링 버퍼는 위 사진처럼 배열의 처음이 끝과 연결되어있다고 보는 자료구조이다.

여기서 논리적으로 어떤 요소가 첫 번째 요소이고 어떤 요소가 마지막 요소인지 식별하기 위한 변수가 프론트(front)와 리어(rear)이다.

프론트와 리어의 값은 인큐와 디큐를 수행함에 따라 변화한다.

이 원리로 인해 요소 이동의 필요가 없어지고 처리의 복잡도는 O(1)이 된다.

IntQueue.h 헤더 만들기

#ifndef ___IntQueue
#define ___IntQueue

typedef struct{
  int max;
  int num;
  int front;
  int rear;
  int *que;
}IntQueue; 

int Initialize(IntQueue *q, int max);

int Enque(IntQueue *q, int x);

int Deque(IntQueue *q, int *x);

int Peek(const IntQueue *q, int *x);

void Clear(IntQueue *q);

int Capacity(const IntQueue *q);

int Size(const IntQueue *q);

int IsEmpty(const IntQueue *q);

int IsFull(const IntQueue *q);

int Search(const IntQueue *q, int x);

void Print(const IntQueue *q);

void Terminate(IntQueue *q);

#endif

헤더에서는 이렇게 큐를 구현하는 구조체부터 저번에 스택을 다뤘던 함수들과 동일한 기능을 다룰 함수들을 선언해주었다.

큐의 최대 용량을 나타내는 max, 현재 요소의 개수를 나타내는 num가 있으며

각각 첫 번째 요소와 맨 나중에 넣은 요소 + 1(앞으로 요소를 넣을 위치)의 인덱스를 저장할 프론트와 리어 그리고 인큐하는 데이터를 저장하기 위한 큐로 사용할 배열의 첫 번째 요소에 대한 포인터인 que가 구조체에 포함된다.

front : 첫 번째 요소의 인덱스

rear : 맨 나중에 넣은 요소 + 1(앞으로 요소를 넣을 위치)의 인덱스

*que : 큐로 사용할 배열의 첫 번째 요소에 대한 포인터

여기서 큐가 비어 있을때는 num과 max의 값이 같다. 이는 프론트와 리어의 값이 같은 경우 큐가 비어 있는지 가득 찼는지 구별할 수 없기 때문에 꼭 필요하다.

링 버퍼로 큐 구현하기

#include "IntQueue.h"
#include <stdio.h>
#include <stdlib.h>

int Initialize(IntQueue *q, int max) {
  q->num = q->front = q->rear = 0;
  if ((q->que = calloc(max, sizeof(int))) == NULL) {
    q->max = 0;
    return -1;
  }
  q->max = max;
  return 0;
}

int Enque(IntQueue *q, int x) {
  if (q->num >= q->max)
    return -1;
  else {
    q->num++;
    q->que[q->rear++] = x;
    if (q->rear == q->max)
      q->rear = 0;
    return 0;
  }
}

int Deque(IntQueue *q, int *x) {
  if (q->num <= 0)
    return -1;
  else {
    q->num--;
    *x = q->que[q->front++];
    if (q->front == q->max)
      q->front = 0;
    return 0;
  }
}

int Peek(const IntQueue *q, int *x) {
  if (q->num <= 0)
    return -1;
  *x = q->que[q->front];
  return 0;
}

void Clear(IntQueue *q) { q->num = q->front = q->rear = 0; }

int Capacity(const IntQueue *q) { return q->max; }

int Size(const IntQueue *q) { return q->num; }

int IsEmpty(const IntQueue *q) { return q->num <= 0; }

int IsFull(const IntQueue *q) { return q->num >= q->max; }

int Search(const IntQueue *q, int x) {
  for (int i = 0; i < q->num; i++) {
    int idx = (i + q->front) % q->max; //어려우니 해설 참고
    if (q->que[idx] == x)
      return idx;
  }
  return -1;
}

void Print(const IntQueue *q) {
  for (int i = 0; i < q->num; i++)
    printf("%d\n", q->que[(i + q->front) % q->max]);
}

void Terminate(IntQueue *q) {
  if (q->que != NULL)
    free(q->que);
  q->max = q->num = q->front = q->rear = 0;
}

이전에 구현한 스택과 같은 기능들을 하는 함수들을 구현해보았다. 다른 함수들은 큰 어려움 없이 구현 했지만 Search 함수의 인덱스를 설정하는 부분은 조금 새로웠다.

전체적으로 스택과 비슷하지만, 인큐와 디큐시에 아래와 같은 코드가 추가되었다.

if (q->rear == q->max)
q->rear = 0;

if (q->front == q->max)
q->front = 0;

링 버퍼로 구현한 큐이기에 front나 rear에 인큐와 디큐를 하다보면 배열의 끝 부분에 도달하게 될 것이고, 이때 배열의 끝에 도달한다면 다시 배열의 앞부분인 0으로 이동시켜주는 코드이다.

Search 함수에서 인덱스 의미

이 함수도 스택을 구현할때와 같이 선형 검색을 사용하는데, 인덱스를 구하는 방법이 신기하다.

(i + q->front) % q->max; 

이처럼 바로 front를 max로 나눈 나머지를 구하는 것이다.

int que[10] = {0, 0, 0, 0, 4, 1, 2, 3, 4, 0};
max = 10;
front = 4;

이와 같은 상태일때 위의 인덱스를 구해보면

i=0 일때 6이 되고

i가 증가함에 따라 7, 8, 9 가 되다가

i=4가 되면 0이 된다

이처럼 링버퍼로 구현한 큐에서 인덱스를 구할때 나머지를 이용하면 쉽게 배열을 링 버퍼로 접근할 수 있다는 걸 깨달았다.

큐를 사용하는 프로그램 구현

#include "IntQueue.h"
#include <stdio.h>
#include <stdlib.h>

int Initialize(IntQueue *q, int max) {
  q->num = q->front = q->rear = 0;
  if ((q->que = calloc(max, sizeof(int))) == NULL) {
    q->max = 0;
    return -1;
  }
  q->max = max;
  return 0;
}

int Enque(IntQueue *q, int x) {
  if (q->num >= q->max)
    return -1;
  else {
    q->num++;
    q->que[q->rear++] = x;
    if (q->rear == q->max)
      q->rear = 0;
    return 0;
  }
}

int Deque(IntQueue *q, int *x) {
  if (q->num <= 0)
    return -1;
  else {
    q->num--;
    *x = q->que[q->front++];
    if (q->front == q->max)
      q->front = 0;
    return 0;
  }
}

int Peek(const IntQueue *q, int *x) {
  if (q->num <= 0)
    return -1;
  *x = q->que[q->front];
  return 0;
}

void Clear(IntQueue *q) { q->num = q->front = q->rear = 0; }

int Capacity(const IntQueue *q) { return q->max; }

int Size(const IntQueue *q) { return q->num; }

int IsEmpty(const IntQueue *q) { return q->num <= 0; }

int IsFull(const IntQueue *q) { return q->num >= q->max; }

int Search(const IntQueue *q, int x) {
  for (int i = 0; i < q->num; i++) {
    int idx = (i + q->front) % q->max; //어려우니 해설 참고
    if (q->que[idx] == x)
      return idx;
  }
  return -1;
}

void Print(const IntQueue *q) {
  for (int i = 0; i < q->num; i++)
    printf("%d\n", q->que[(i + q->front) % q->max]);
}

void Terminate(IntQueue *q) {
  if (q->que != NULL)
    free(q->que);
  q->max = q->num = q->front = q->rear = 0;
}

void main(){
  IntQueue que;
  int value;
  printf("생성할 배열의 크기 : ");
  scanf("%d", &value);
  if(Initialize(&que, value) == -1){
    puts("\n큐 생성 실패");
  }
  while(1){
    int m, x; 

    printf("\n현재 데이터 수 : %d / %d\n", Size(&que), Capacity(&que));
    printf("(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : ");
    scanf("%d", &m);

    if(m==0) break;
    switch(m){
      case 1:
        printf("\n데이터 : "); scanf("%d", &x);
        if(Enque(&que, x)==-1) puts("\n인큐 실패");
        break;

      case 2:
        if(Deque(&que, &x) == -1) puts("\n디큐 실패");
        else printf("\n디큐한 데이터 : %d\n", x);
        break;

      case 3:
        if(Peek(&que, &x) == -1) puts("\n피크 실패");
        else printf("\n피크한 데이터 : %d\n", x);
        break;

      case 4:
        Print(&que);
        break;
    }
  }
  Terminate(&que);
}

인큐와 디큐, 피크, 출력 기능을 가진 프로그램을 짜보았다.

이렇게 짠 링 버퍼는 오래된 데이터를 버리는 용도로 사용할 수 있다.

요소의 개수가 n인 배열에 계속해서 데이터가 입력될 때 가장 오래된 데이터는 버려지고 그 자리에 데이터를 입력함으로써 가장 최근에 들어온 데이터 n개만 저장할 수 있다.

다음에는 내가 보는 책에는 없지만 추가적으로 공부하다 알게 됀 덱(Deque)이라는 자료구조에 대해 다뤄보겠다.